JUMP TO TOPIC

As one delves into the diverse and fascinating world of geometry, the Nonagon emerges as a figure of intrigue, brimming with unique properties and applications. One such figure is the Nonagon, a polygon defined by nine equal sides. Although it may not be as commonly recognized as the triangle or square, the Nonagon carries its own allure, from the intricacy of its internal angles to the symmetrical beauty of its form. This nine-sided polygon finds its place in a myriad of applications – whether in the architectural splendor of historical buildings or the strategic layouts in board games.
This article aims to illuminate the intriguing characteristics, mathematical principles, and real-world applications of the Nonagon, unearthing the appeal and significance of this nine-sided geometric figure.
Definition
A nonagon, sometimes referred to as an enneagon, is a closed geometric figure that is defined as a two-dimensional polygon with nine sides and nine angles. Originating from the Latin prefix “nona-” meaning “nine” and the Greek suffix “-gon,” meaning “corner” or “angle,” the term “nonagon” quite literally translates to “nine angles.” Similarly, “enneagon” is composed of the Greek words “ennea,” meaning “nine,” and “gonia,” meaning “angle.”
Each of these nine sides forms the boundary of the Nonagon and intersects with two other sides at each of its endpoints, resulting in a total of nine vertices or corners. These intersections form the Nonagon’s internal angles. The sum of these internal angles in any nonagon, regardless of whether its sides and angles are equal, is always 1,260 degrees.
Nonagons can be found in a variety of mathematical and real-world contexts, and their properties can be explored and calculated using the principles of geometry. Despite their relative simplicity, nonagons exhibit a fascinating range of geometric and symmetrical properties, making them a rich area of study in the realm of polygonal geometry. Below is the generic diagram for a Nonagon.
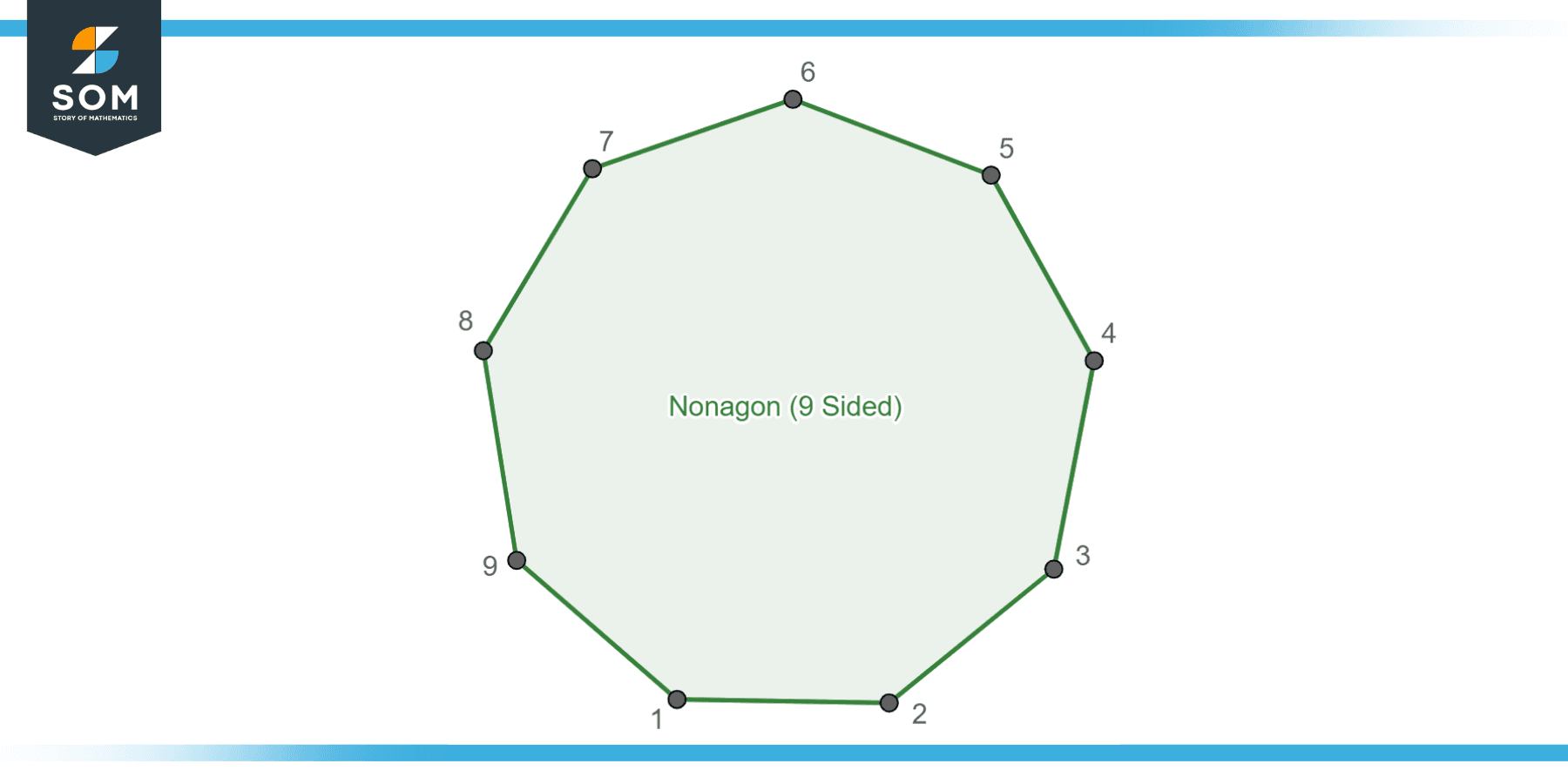
Figuer-1: Generic nonagon.
Historical Significance
The Nonagon, or enneagon, has a unique historical and cultural significance, making appearances in a variety of contexts across different periods and cultures. Here are a few instances where the Nonagon holds historical importance.
Architecture and Design
Nonagonal architectural structures, though less common than structures based on other polygons, have been used throughout history due to their aesthetic appeal and functional design. For instance, the Chapel of the Ascension in Jerusalem, a site of significant historical and religious importance, was originally built as a nonagon.
Religious Symbolism
The Nonagon holds significance in various spiritual and mystical traditions. In the Baha’i faith, the Nonagon is an important symbol as the Baha’i House of Worship (or temple) is built in the form of a nonagon, signifying the unity of world religions.
Art and Culture
The Nonagon has been used in artistic contexts for its aesthetic appeal and symbolic associations. An example is the Enneagonal (Nine-sided) Monument in Springwood, Australia, which has historical significance as a World War I memorial.
Mathematics and Geometry
The study of nonagons has been a part of mathematical and geometric exploration throughout history. Ancient Greek mathematicians were particularly interested in the properties of polygons, including nonagons.
Symbolism in Literature
The Nonagon has also been used symbolically in literature due to its nine sides. The number nine often signifies completion or the end of a cycle, adding a layer of symbolic significance to the Nonagon’s use.
Nonagon’s Geometry
A nonagon, also known as an enneagon, is a geometric shape that is classified as a polygon. Like all polygons, a nonagon is a two-dimensional figure with straight sides. The distinguishing feature of a nonagon is that it has nine sides and, consequently, nine angles.
One way to visualize the geometry of a nonagon is to imagine a nearly round shape but with flat edges instead of a smooth curve. If the Nonagon is regular, meaning that all its sides and angles are equal, it will appear symmetrical and balanced. Each internal angle in a regular nonagon measures 140 degrees, adding up to a total of 1260 degrees for the sum of internal angles. The more equal the sides and angles, the more the Nonagon will resemble a circle.
In contrast, an irregular nonagon, which does not have equal sides and angles, can have a wide variety of shapes. Irregular nonagons are much more common in natural and human-made environments, as they offer more flexibility and adaptability. Regardless of whether a nonagon is regular or irregular, the sum of its internal angles will always be 1260 degrees.
The geometry of the Nonagon plays a role in various mathematical calculations, including the calculation of area, perimeter, and the properties of diagonals. While the geometry of nonagons might be slightly more complex than simpler polygons like triangles or squares, they offer an interesting field of study in geometry with numerous practical applications.
.
Related Formulae
For a regular nonagon, which has equal side lengths and equal angles, there are several key mathematical formulas:
The sum of Interior Angles
The formula for the sum of the interior angles of any polygon is given by (n-2) × 180, where n is the number of sides. So, for a nonagon (n=9), the sum of the interior angles is (9-2) × 180 = 1260 degrees.
The measure of Each Interior Angle
For a regular nonagon, each interior angle is equal. It is given by the sum of interior angles divided by the number of sides. So, each angle of regular nonagon measures 1260/9 = 140 degrees.
Perimeter
The perimeter of a nonagon is the sum of all its sides. For a regular nonagon, all sides are equal in length, so the perimeter (P) is given by 9 times the length of a side (s). Hence, P = 9 × s.
Area
The area (A) of a regular nonagon can be calculated using the formula:
A = (9/4) × s² × cot(π/9)
where s is the length of a side, and cot is the cotangent function.
Radius of Circumscribed Circle
The radius (R) of the circumscribed circle (a circle that passes through all the vertices of the Nonagon) can be calculated using the formula:
R = 0.5 × s / sin(π/9)
Radius of Inscribed Circle
The radius (r) of the inscribed circle (a circle that touches all the sides of the Nonagon) can be calculated using the formula:
r = 0.5 × s × tan(π/9)
Nonagon Types
Nonagons, like other polygons, can be classified into two main types based on their sides and angles. These are;
Regular Nonagon
A regular nonagon is a nonagon in which all the sides and all the angles are equal. This means that each side of the polygon has the same length, and each angle measures the same.
In a regular nonagon, the internal angle of each corner is exactly 140 degrees. This is because the sum of internal angles in any nonagon is 1260 degrees (derived from the formula (n-2) × 180, where n is the number of sides), and this total is equally distributed in a regular nonagon as all angles are equal.
Because of this property of equal sides and angles, regular nonagons exhibit symmetry, which can be rotational (the shape looks the same after a certain amount of rotation) or reflective (the shape can be reflected over a line and look the same). Below we present the generic diagram for a regular Nonagon.
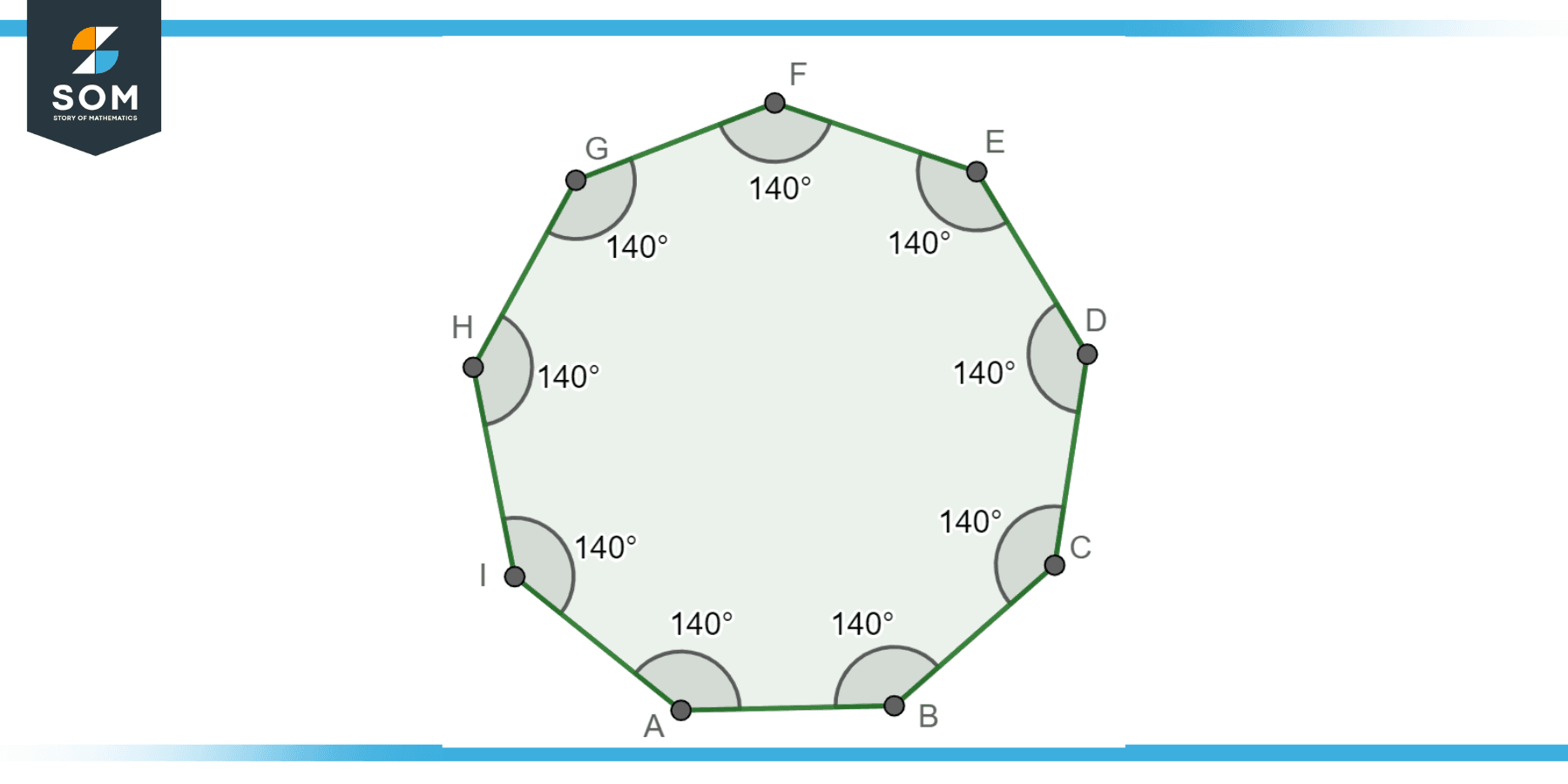
Figuer-2: Regular nonagon.
Irregular Nonagon
An irregular nonagon does not have sides and angles of equal measure. This means that the lengths of the sides can vary, as can the measures of the angles.
While the sum of the internal angles in an irregular nonagon is the same as a regular nonagon, i.e., 1260 degrees, the individual angles can be different from each other. Similarly, while the lengths of the sides can be different, they all should add up to the total perimeter of the shape.
Unlike regular nonagons, irregular nonagons do not necessarily exhibit symmetry. The lack of uniformity can make these shapes more complex and difficult to analyze geometrically than their regular counterparts. Below we present the generic diagram for an irregular nonagon.
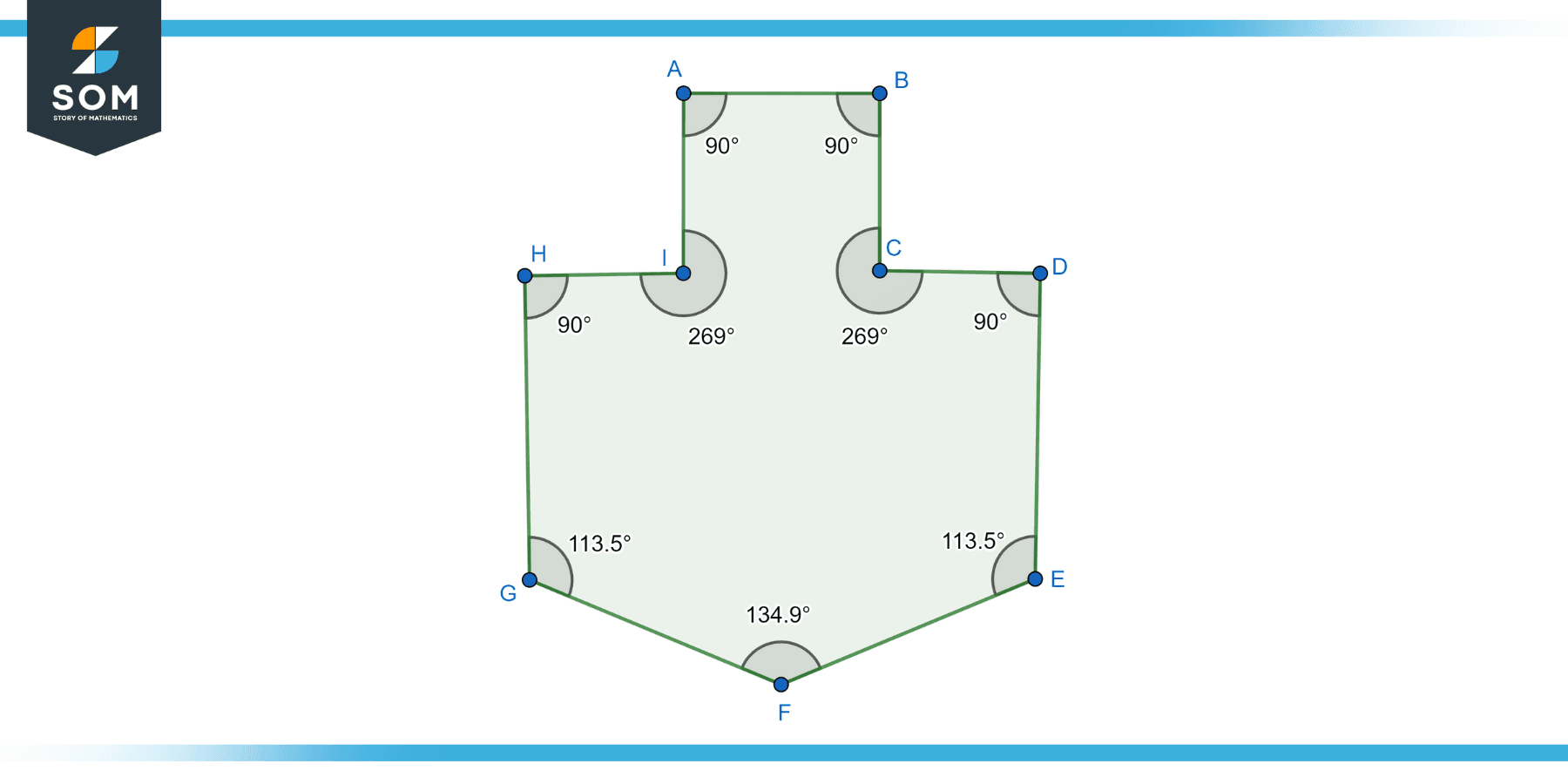
Figuer-3: Irregular nonagon.
Irregular nonagons can be further classified into two types: convex and concave.
Convex Irregular Nonagon
A Convex Irregular Nonagon is a nine-sided polygon in which all interior angles are less than 180 degrees. The term “irregular” implies that the lengths of the sides and the measures of the angles can be different from one another, and “convex” signifies that no angle measures more than 180 degrees.
Key properties of a Convex Irregular Nonagon include:
Nine Sides and Nine Vertices
Like all nonagons, it has nine sides (edges) and nine vertices (corners).
Interior Angles
All interior angles in a convex nonagon are less than 180 degrees.
The sum of Interior Angles
The sum of the interior angles of any nonagon, whether it’s convex or not, is always 1260 degrees.
External Angles
Each exterior angle, if extended, will not intersect the polygon except at its own vertices.
Lines Drawn
Any line segment drawn between two vertices will always lie inside the polygon. Below we present the generic diagram for an irregular convex nonagon.
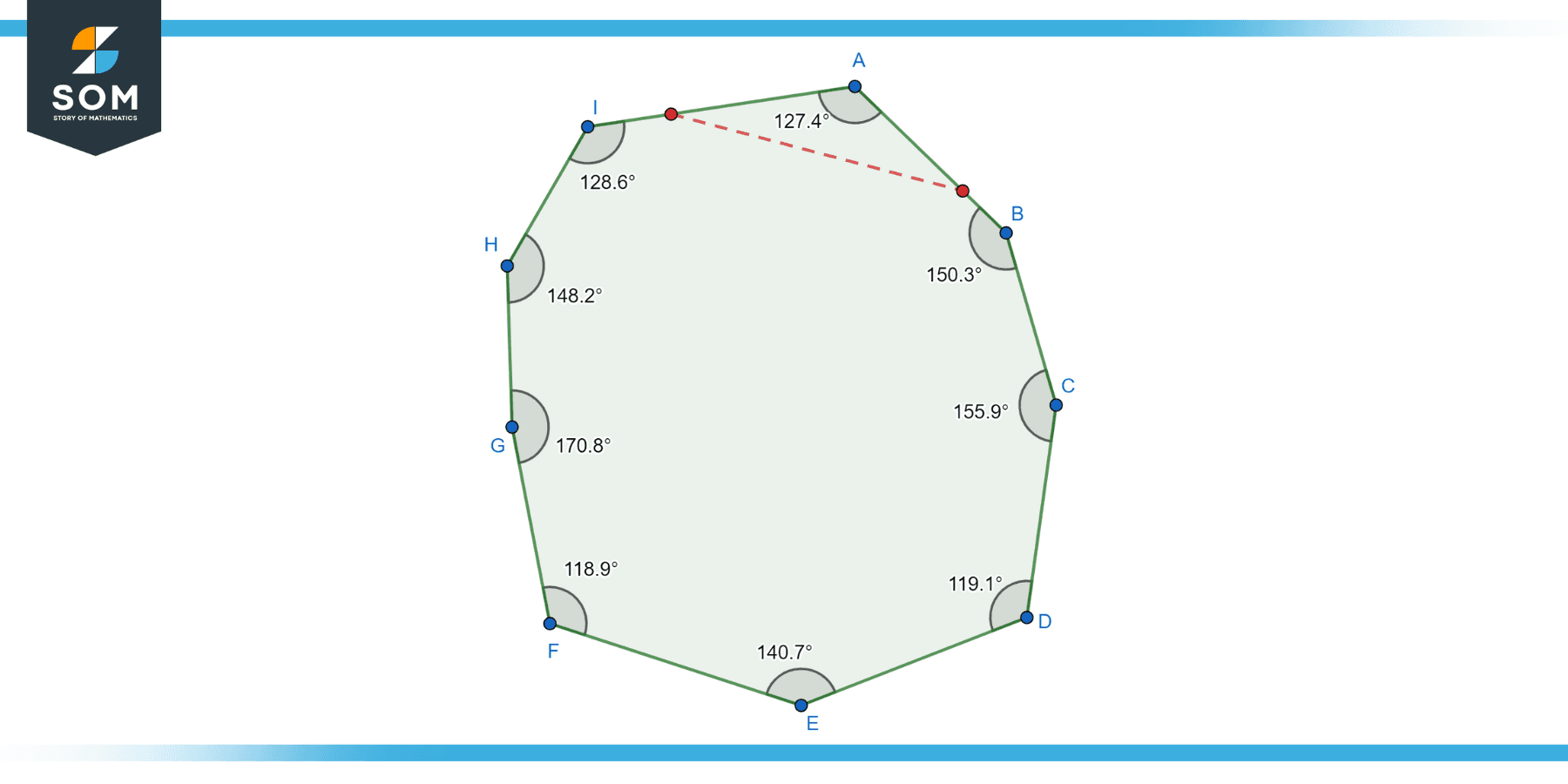
Figuer-4: Irregular convex nonagon.
Concave Irregular Nonagon
A Concave Irregular Nonagon, on the other hand, is a nine-sided polygon with at least one interior angle greater than 180 degrees. This means that at least one vertex points inward, away from the “center” of the figure, creating what appears to be a ‘dent’ in the side of the polygon.
Key properties of a Concave Irregular Nonagon include:
Nine Sides and Nine Vertices
Like all nonagons, it has nine sides (edges) and nine vertices (corners).
Interior Angles
At least one of the interior angles in a concave nonagon is greater than 180 degrees.
The sum of Interior Angles
Regardless of its shape, the sum of the interior angles of any nonagon, including concave nonagons, is 1260 degrees.
External Angles
At least one exterior angle, if extended, will intersect the polygon at some point other than its own vertices.
Lines Drawn
A line segment drawn between certain pairs of vertices will lie outside the polygon. Below we present the generic diagram for an irregular concave nonagon.
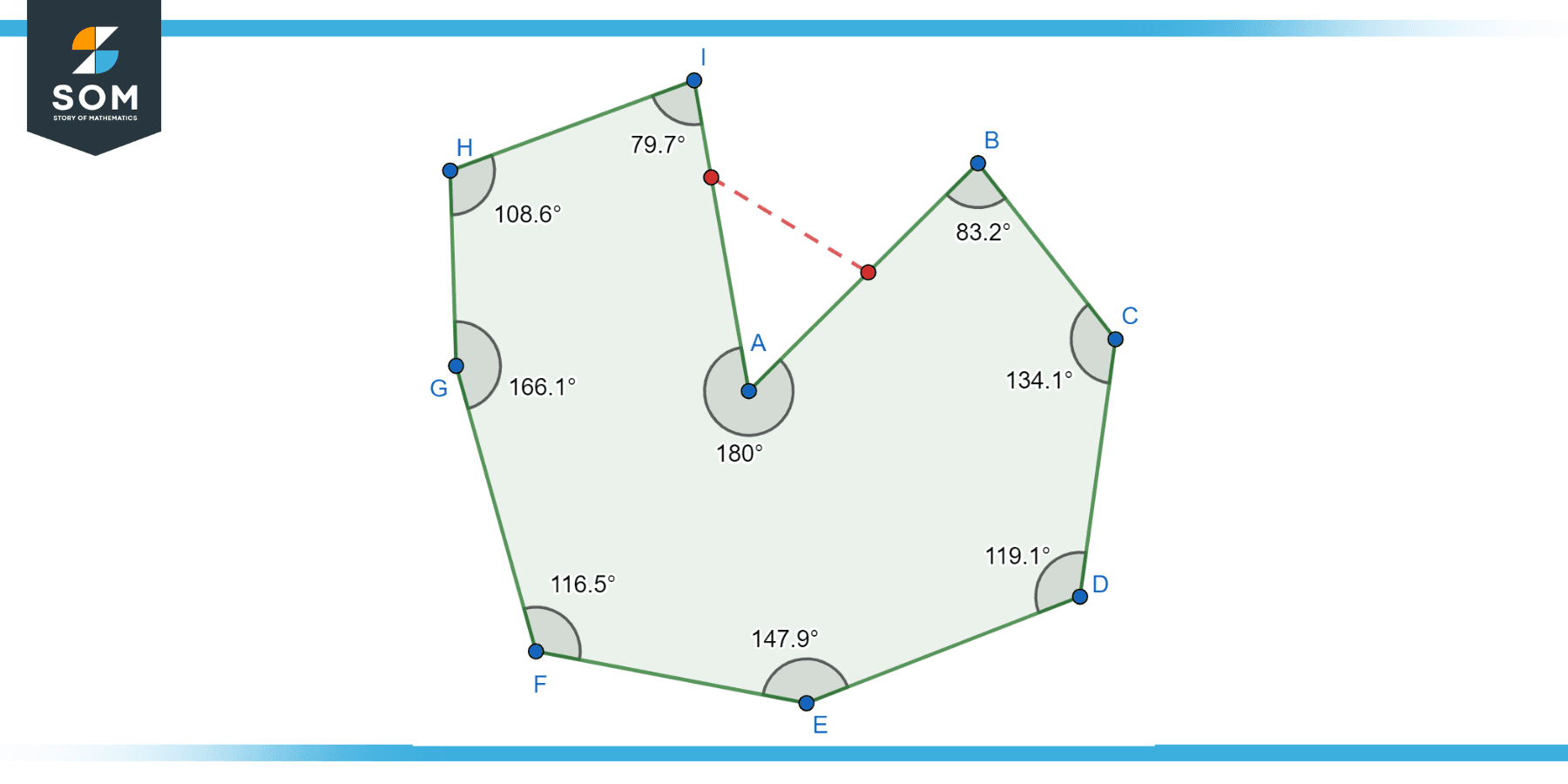
Figuer-5: Irregular concave nonagon.
Applications
The nonagon, though less common than other geometric shapes, finds applications in a variety of fields, including art, architecture, design, and science. Here are a few specific examples:
Architecture
Nonagons are found in various architectural structures, from buildings to city layouts. Due to the near-circular nature of a nonagon, it allows a large interior space without needing any internal support. A famous example is the Baha’i House of Worship. All Baha’i temples around the world follow a nonagonal structure. Each temple has nine doors that open onto a central hall, signifying the unity of all religions.
Art and Design
Nonagons provide an aesthetic appeal in the realm of visual arts and graphic design. They serve as a source of symmetry and balance. In tiling and tessellations, regular nonagons can be used to create intriguing patterns, offering a refreshing deviation from the common use of squares, rectangles, and hexagons.
Games and Puzzles
Nonagons also find applications in recreational areas like board games and puzzles. For instance, certain strategy-based board games might use a nonagonal board or nonagonal tiles to add complexity and variation to the gameplay. In puzzles, especially those involving geometric problem-solving, nonagons may be used to challenge conventional thinking.
Mathematics and Geometry
In the realm of geometry, nonagons play a crucial role in understanding the properties and behaviors of polygons. Studying how to calculate the area, perimeter, and angles of a nonagon offers an interesting foray into geometric principles. Nonagons can also be used to construct complex polyhedra, further extending their use in mathematical explorations.
Symbolic Representations
Nonagons are used symbolically in various cultural and religious contexts. In the Baha’i faith, the nine sides of the Nonagon symbolize the unity of the world’s major religions, reinforcing the Baha’i principle of religious unity. The number nine also carries significance in numerology and can represent completion or finality in certain cultural contexts.
Urban Planning and Design
Nonagons have potential applications in urban design and city planning. For example, a nonagonal layout can be used for a park, creating interesting pathways and sightlines. Traffic roundabouts could be designed with a nonagonal shape, providing more entry and exit points and potentially improving traffic flow.
The U.S. Pentagon Building
While it’s true that the Pentagon is famous for its five sides, the central plaza within the Pentagon building, known as the “Ground Zero Cafe,” is actually a regular nonagon. This nine-sided courtyard area is an excellent real-world example of a nonagon, albeit within the structure of a pentagonal building.
Coins
The British 50 pence coin and the Australian 50 cent coin are examples of nonagons in everyday life. Although at first glance they may seem round, they are actually equilateral curved heptagons with nine sides.
Exercise
Example 1
Find the sum of the interior angles of a nonagon.
Solution
The formula to find the sum of interior angles of any polygon is (n-2) × 180, where n is the number of sides.
For a nonagon, n = 9.
Therefore, the sum of interior angles = (9-2) × 180 = 1260 degrees.
Example 2
Find the measure of each interior angle of a regular nonagon.
Solution
Each interior angle of a regular nonagon is equal and can be calculated by dividing the sum of interior angles by the number of sides.
Each interior angle = Sum of interior angles/number of sides
Each interior angle = 1260 / 9
Each interior angle = 140 degrees
Example 3
Calculate the perimeter of the Nonagon.
Solution
The perimeter of a regular nonagon is the sum of all its sides.
Perimeter = 9 × s
Perimeter = 9 × 5
Perimeter = 45 cm
Example 4
Determine the area of the Nonagon given in Figure-6.
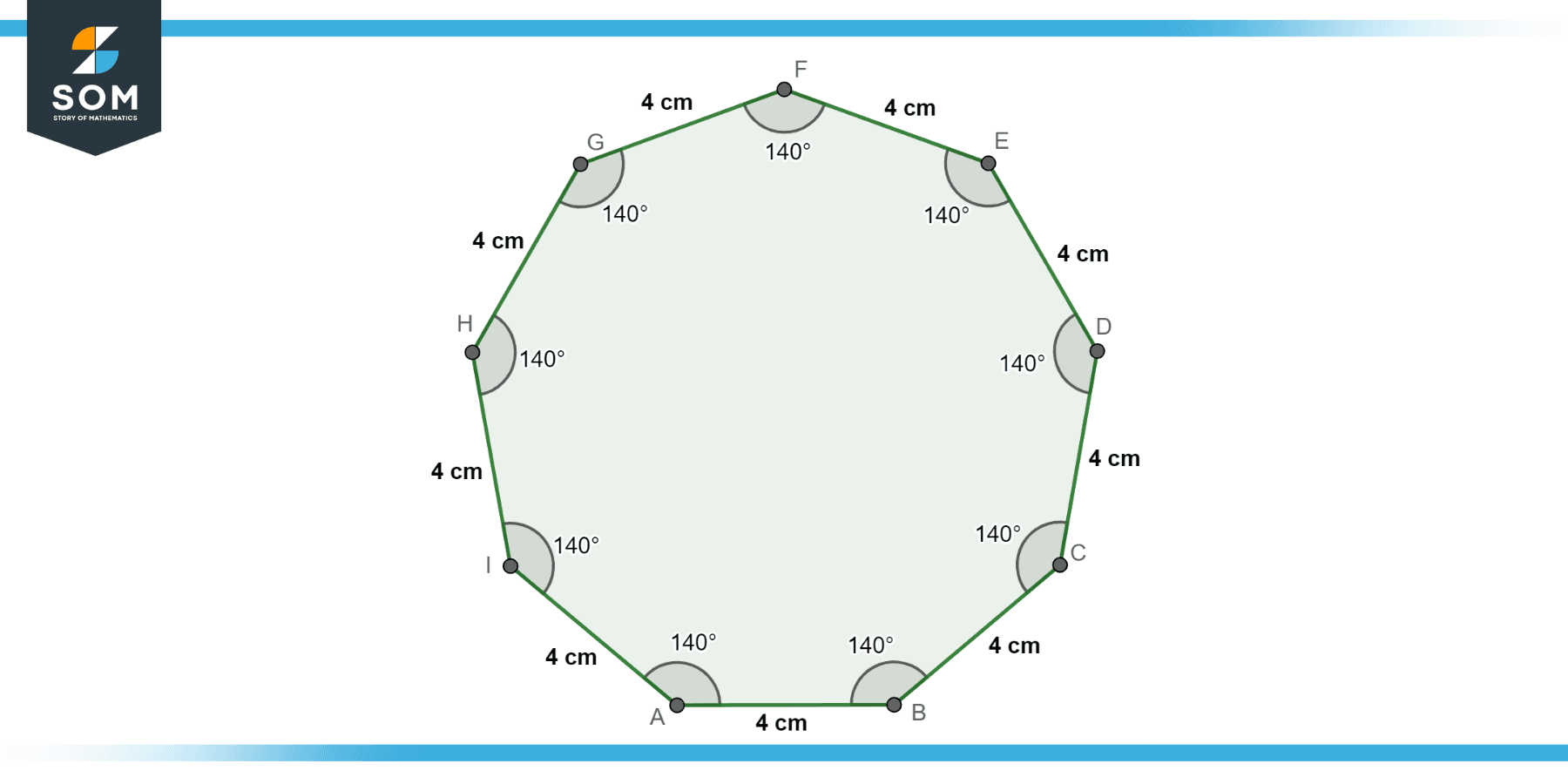
Figuer-6.
Solution
The formula for the area of a regular nonagon is:
Area = (9/4) × s² × cot(π/9)
Therefore, substituting the given side length (s) into the formula,
Area = (9/4) × 4² × cot(π/9)
Area ≈ 97.38 cm²
Example 5
Compute the radius of the circumscribed circle in a regular nonagon with a side length of 6 cm.
Solution
The radius of the circumscribed circle can be calculated using the formula:
Radius = 0.5 × s / sin(π/9)
Substituting the given side length into the formula,
Radius = 0.5 × 6 / sin(π/9)
Radius ≈ 9.66 cm
Example 6
Compute the radius of the inscribed circle in a regular nonagon with side length (s) of 3 cm.
Solution
The radius of the inscribed circle can be calculated using the formula:
Radius = 0.5 × s × tan(π/9)
Substituting the given side length into the formula,
Radius = 0.5 × 3 × tan(π/9)
Radius ≈ 1.01 cm
Example 7
What are the number of triangles the Nonagon can be divided into?
Solution
A polygon can be divided into (n-2) triangles, where n is the number of sides.
For a nonagon, n = 9.
Therefore, the number of triangles = 9 – 2 = 7 triangles
Example 8
Compute the number of diagonals in a nonagon.
Solution
The formula for the number of diagonals (d) in a polygon is given by n × (n-3)/2, where n is the number of sides.
For a nonagon, n = 9. Substituting into the formula gives:
d = 9 × (9-3)/2 = 27 diagonals.
All images were created with GeoGebra.
