
At the heart of geometry lies the humble triangle, a shape of utmost importance due to its structural stability and its inherent presence in many forms around us. Of all triangle types, the isosceles triangle stands out for its notable properties of symmetry. Characterized by two sides of equal length, known as the legs, and a distinct third side called the base, isosceles triangles make an intriguing study. The base angles, or the angles formed between each leg and the base, are equal in measure, a feature that adds to the symmetrical allure of these geometric figures.
In this article, we will explore the defining features, properties, formulas, and practical applications of the isosceles triangle, providing a comprehensive understanding of this remarkable geometric shape.
Definition
An isosceles triangle is a type of triangle that has two sides of equal length. These equal sides are known as the legs of the triangle, and the third side is known as the base. The base angles of an isosceles triangle, which are the angles opposite the two equal sides, are themselves equal in measure.
An isosceles triangle is a fascinating geometric shape that possesses unique properties and characteristics. It is defined by its distinct symmetry, where two sides of the triangle are of equal length, and the remaining side is different in length. The term “isosceles” is derived from the Greek words “isos,” meaning “equal,” and “skelos,” meaning “leg.” This captivating triangle has been studied for centuries and finds applications in various fields, including mathematics, engineering, architecture, and art. Below we present the generic diagram for an isosceles triangle.
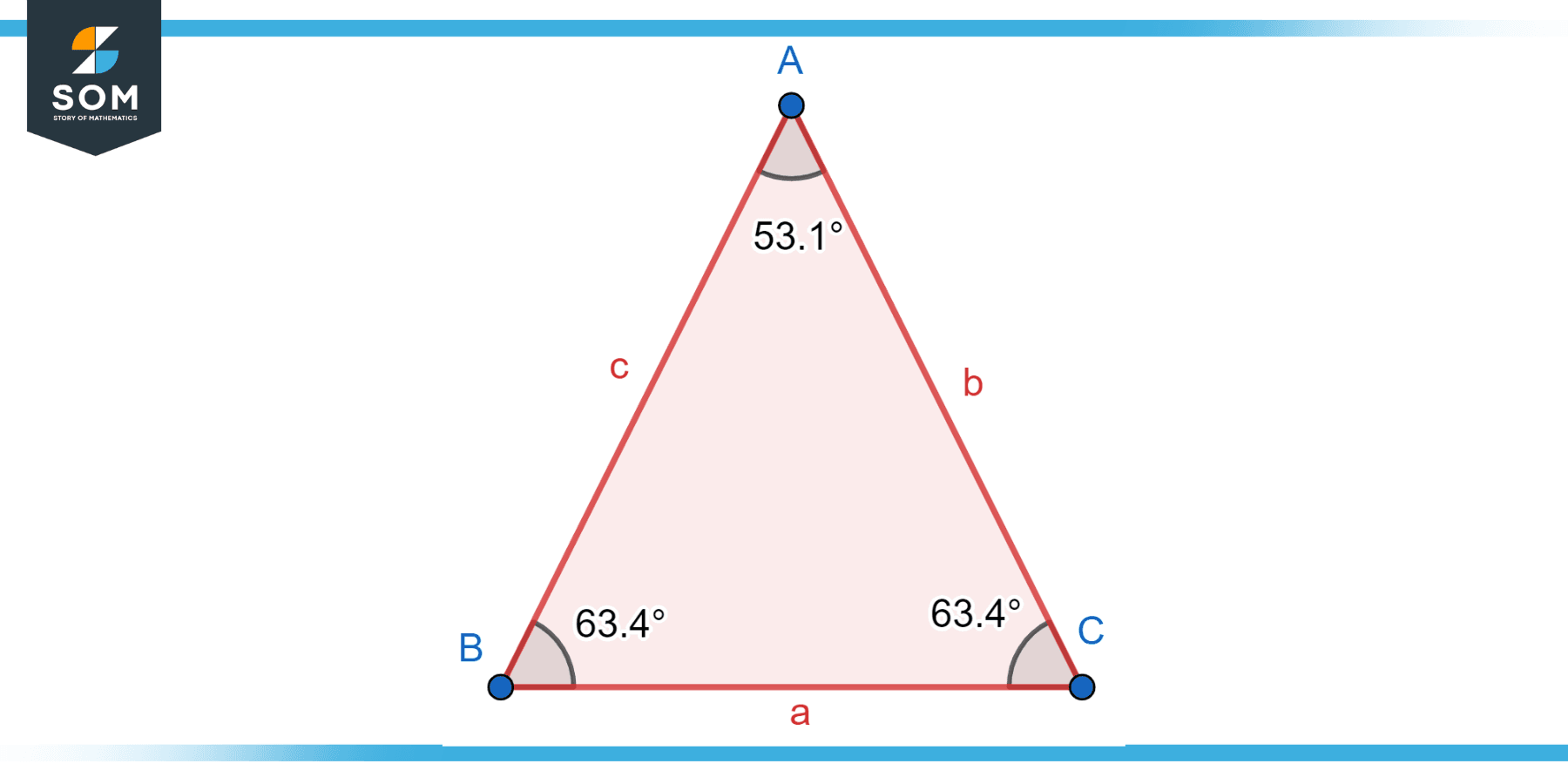
Figure-1: Isosceles triangle.
Historical Significance
The isosceles triangle, like many geometric concepts, has a rich and fascinating historical background. Its study can be traced back to some of the earliest civilizations and has deeply influenced the development of mathematical theory.
The term “isosceles” itself derives from the ancient Greek words “isos,” meaning “equal,” and “skelos,” meaning “leg.” Literally translated, it means “equal-legged,” pointing towards its defining property of having two sides of equal length.
The earliest written records discussing isosceles triangles date back to ancient Egypt, particularly the Rhind Mathematical Papyrus, which is one of the oldest known mathematical documents, dating around 1650 BC. This document presents problems and solutions that involve isosceles triangles, highlighting their significance even in these early civilizations.
The ancient Greeks further developed the study of isosceles triangles, most notably through the work of Euclid, a mathematician often referred to as the “father of geometry.” His seminal work, Euclid’s Elements, compiled around 300 BC, devotes significant attention to isosceles triangles. In particular, Proposition 5 of Book 1 in Euclid’s Elements establishes that the base angles of an isosceles triangle are equal, one of the defining properties of this geometric shape.
In India, the famous mathematician-astronomer Aryabhata, in his treatise Aryabhatiya written in 499 AD, utilized the properties of isosceles triangles for astronomical calculations.
The significance of the isosceles triangle transcends mathematics and can be seen in various other fields. For example, in architecture and engineering, the properties of isosceles triangles are often used to ensure stability and balance. Additionally, in art and design, isosceles triangles are commonly used due to their pleasing aesthetic properties.
Thus, the isosceles triangle, with its symmetry and unique properties, has had a profound impact on the development of mathematical theory, practical applications, and aesthetic principles throughout history.
Properties
The isosceles triangle is an important geometric figure with several defining properties. Here they are in detail:
Equal Sides:
n isosceles triangle has two sides of equal length. These equal sides are often referred to as the legs of the triangle.
Equal Angles
Corresponding to the two equal sides are two angles of equal measure. These are called base angles, and they are located opposite the two equal sides. This is a crucial property that derives from the equality of the two sides.
Vertex Angle
The angle formed by the two equal sides is known as the vertex angle. It is located between the two equal sides.
Altitude, Angle Bisector, and Median
In an isosceles triangle, the altitude (or height) drawn from the vertex angle (the angle between the two equal sides) to the base, the angle bisector of the vertex angle, and the median to the base (line drawn from the vertex angle to the midpoint of the base) are all the same line. This line is also the line of symmetry of the triangle, dividing it into two congruent right triangles.
Sum of Angles
As with any triangle, the sum of the internal angles of an isosceles triangle is 180 degrees. Given the equality of the base angles, if you know the measure of the vertex angle, you can easily calculate the base angles’ measure and vice versa.
Perimeter
The perimeter of an isosceles triangle, like any other triangle, is the sum of the lengths of its three sides.
Area
The area of an isosceles triangle can be calculated using the formula 1/2 * base * height. For an isosceles triangle, the height is the length of the altitude drawn from the vertex to the base.
These properties make the isosceles triangle a fascinating subject in geometry, with many practical applications in areas such as engineering, architecture, and design due to its inherent symmetry and balance.
Relevant Formulas
An isosceles triangle, a triangle with two sides of equal length, has a few key formulas related to it. Here they are in detail:
Perimeter
The perimeter of an isosceles triangle (or any triangle) is calculated by adding the lengths of its three sides. If the lengths of the two equal sides are a and the base’s length is b, the perimeter is calculated as P = 2 × a + b.
Area
The area of an isosceles triangle is found by the formula A = 1/2 × base × height. If the base length is b and the height (the line perpendicular from the base to the opposite vertex) is h, the area is A = 1/2 × b × h.
Height
If the lengths of the two equal sides (a) and the base (b) are known, the height can be found using the Pythagorean theorem. It splits the base into two segments of length b/2 each, forming two right triangles. The height (h) is then given by h = √(a² – (b/2)²).
Base Angles
Since an isosceles triangle has two equal sides, the angles opposite these sides (known as base angles) are also equal. If the vertex angle (the angle between the two equal sides) is known, the base angles can be calculated. If the vertex angle is θ, then each base angle is (180 – θ)/2 (since the sum of all angles in a triangle is 180 degrees).
Using the Law of Cosines
In situations where the lengths of all sides are known, but the angles aren’t, the Law of Cosines is a useful tool. It states that for any triangle with sides of lengths a, b, and c, and an angle γ opposite side c, the following relationship holds: c² = a² + b² – 2ab × cos(γ). In an isosceles triangle with equal sides of length a and base of length b, if we wish to find the vertex angle (θ), we can rearrange the Law of Cosines as cos(θ) = (2a² – b²) / (2a²).
These formulas encapsulate the primary quantitative characteristics of isosceles triangles and are fundamental tools in the study and application of geometry.
Types
Isosceles triangles, defined by their two sides of equal length, can be categorized into different types based on their internal angles. Here are the main types explained in detail:
Equilateral Isosceles Triangle
In an equilateral triangle, all three sides are equal in length. This equality in length also implies equality in the internal angles. Thus, all three internal angles of an equilateral triangle are equal. Given that the sum of the internal angles of a triangle is 180 degrees, each angle in an equilateral triangle measures exactly 60 degrees. It’s worth noting that while all equilateral triangles are isosceles, not all isosceles triangles are equilateral. Below we present the generic diagram for an equilateral isosceles triangle.
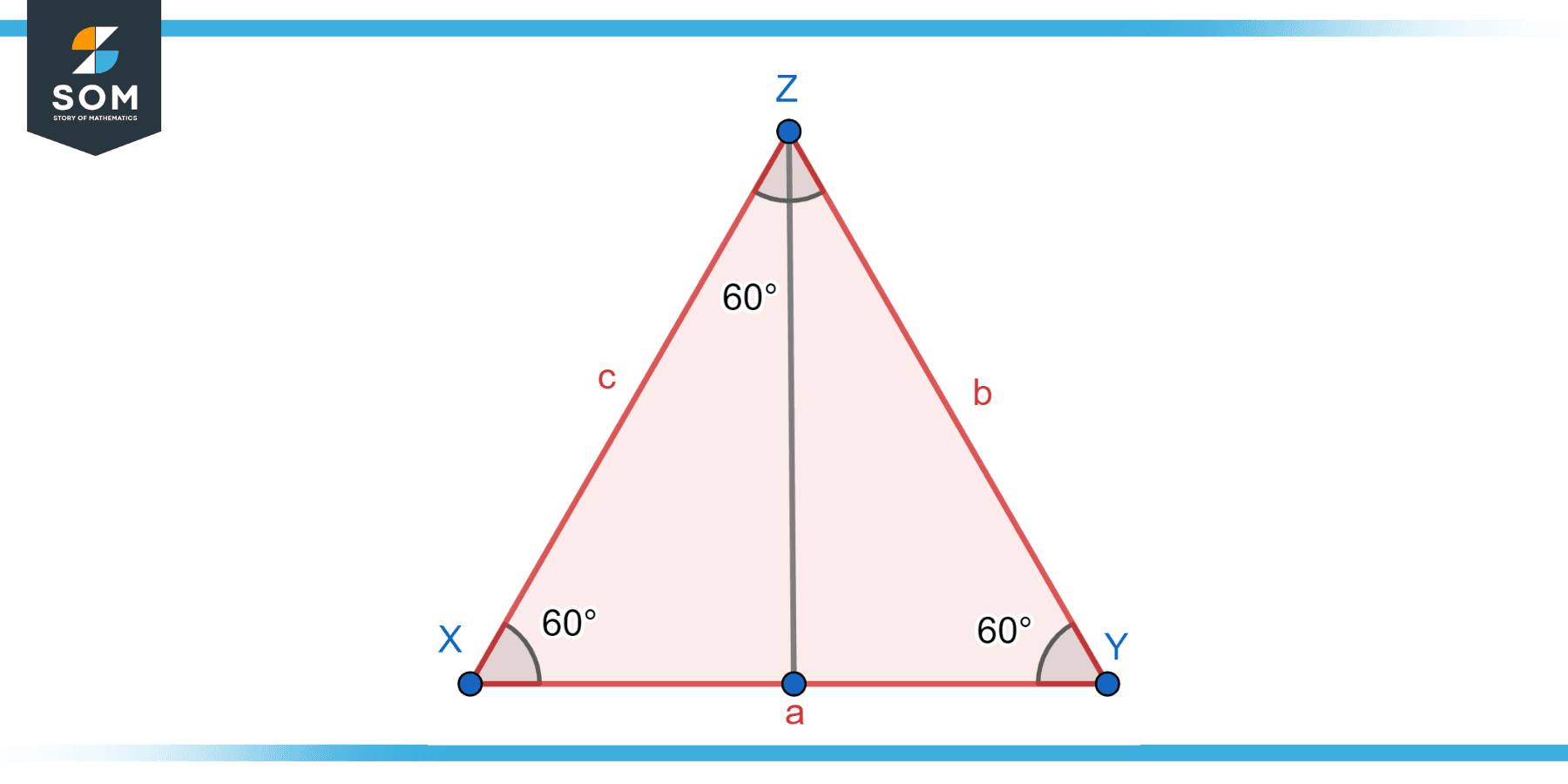
Figure-2: Equilateral isosceles triangle.
Acute Isosceles Triangle
In an acute isosceles triangle, the vertex angle, or the angle between the two equal sides, is an acute angle. This means it measures less than 90 degrees. The other two base angles are also acute and equal to each other. This makes all three angles in an acute isosceles triangle less than 90 degrees, hence the name. Below we present the generic diagram for an acute isosceles triangle.
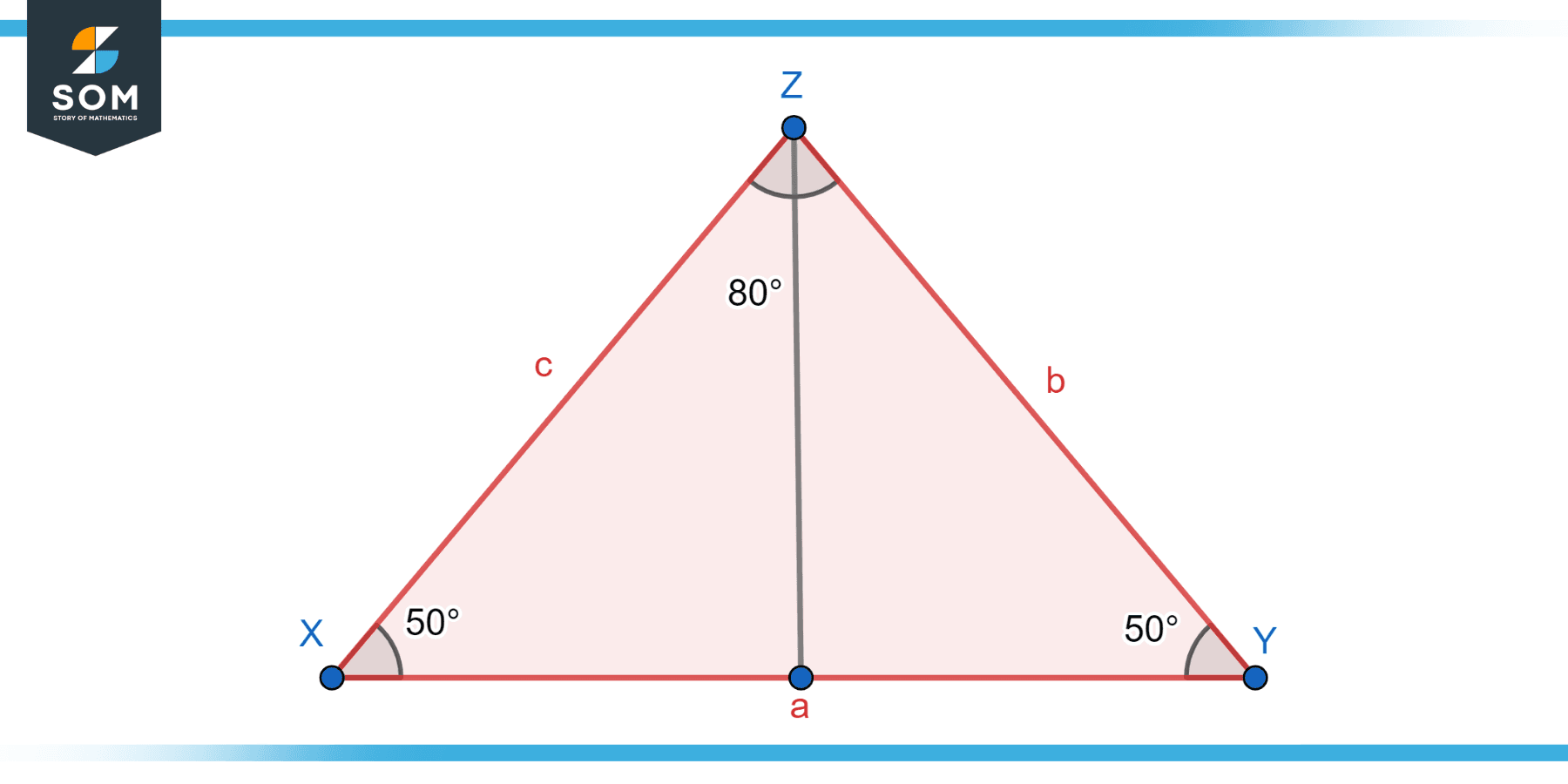
Figure-3: Acute isosceles triangle.
Right Isosceles Triangle
A right isosceles triangle features a vertex angle that is a right angle, measuring precisely 90 degrees. The other two base angles in this type of triangle are equal, each measuring 45 degrees due to the symmetry of the triangle and the requirement that all angles in a triangle add up to 180 degrees. This type of triangle is useful in various areas, including geometry and trigonometry, due to its unique properties. Below we present the generic diagram for a right isosceles triangle.
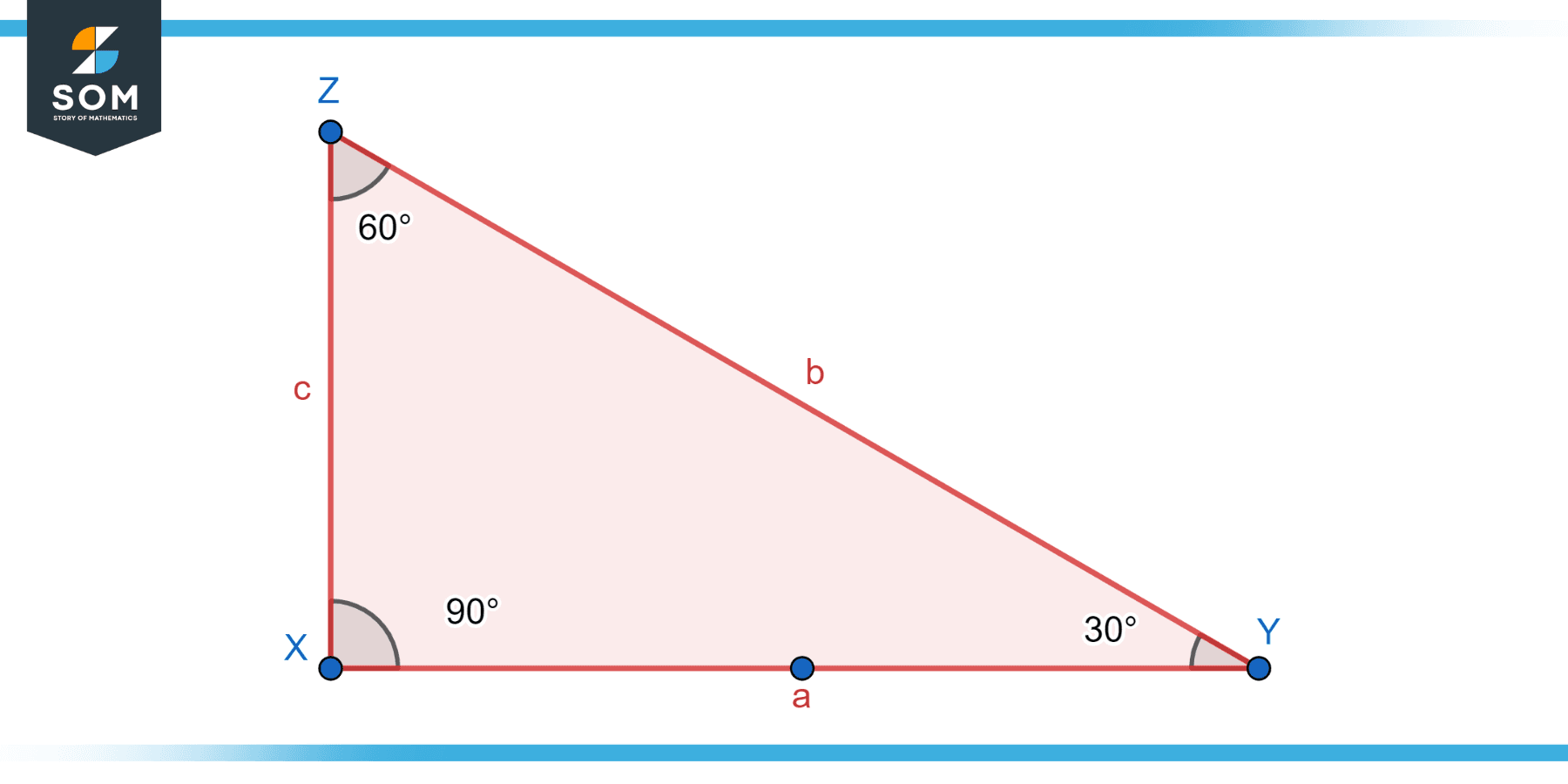
Figure-4: Right isosceles triangle.
Obtuse Isosceles Triangle
In an obtuse isosceles triangle, the vertex angle is an obtuse angle. This means it measures more than 90 degrees but less than 180 degrees. The other two base angles are acute and equal to each other. Because of the obtuse angle, this type of triangle has a visibly “stretched” appearance, with one corner being notably wider than the others. Below we present the generic diagram for an obtuse isosceles triangle.
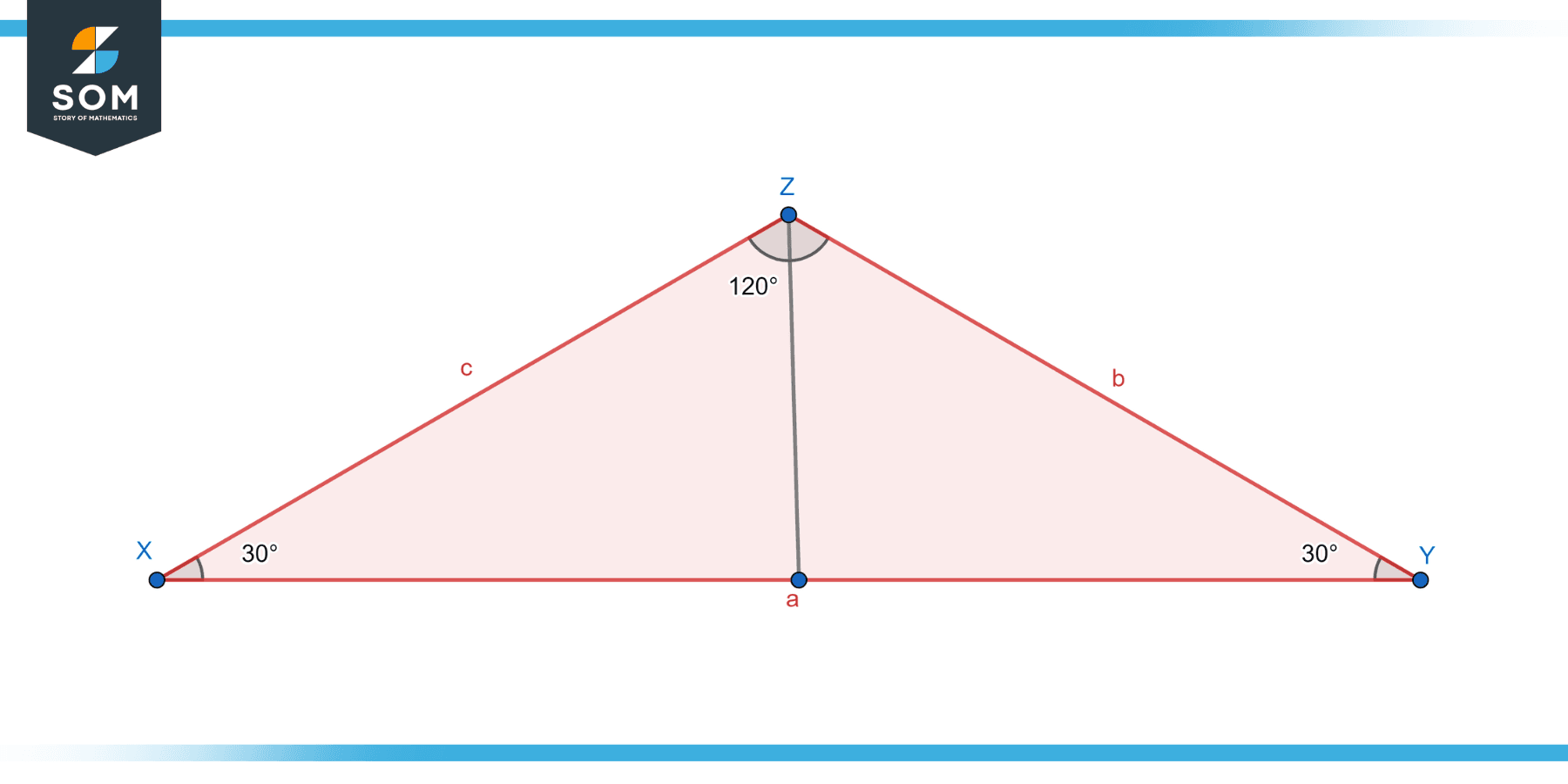
Figure-5: Obtuse isosceles triangle.
Regardless of the specific type of isosceles triangle, one constant rule in geometry is the fact that the sum of the internal angles of a triangle always adds up to 180 degrees. This, in conjunction with the rule that the two base angles of an isosceles triangle are equal, allows us to calculate the measures of unknown angles given certain information.
Applications
The isosceles triangle, with its distinct properties and versatile nature, finds applications in various fields. Here are some notable applications of the isosceles triangle in different disciplines.
Architecture and Engineering
Isosceles triangles play a significant role in architectural and engineering design. Their symmetrical properties make them useful in creating stable and balanced structures. Isosceles triangles are commonly employed in the construction of roofs, trusses, and arches, where their geometry provides strength and support.
Art and Design
The isosceles triangle is frequently utilized in art and design compositions. Its symmetrical shape and balanced proportions make it visually appealing and versatile in creating aesthetically pleasing arrangements. Isosceles triangles can be found in various art forms, such as paintings, sculptures, and graphic design.
Mathematics and Geometry
The isosceles triangle holds a significant place in mathematics and geometry. It serves as a fundamental building block for exploring geometric concepts and theorems. The properties of isosceles triangles contribute to the understanding of triangle congruence, similarity, and the Pythagorean theorem.
Surveying and Navigation
Isosceles triangles are used in surveying and navigation to calculate distances and angles. They play a vital role in triangulation methods, where measurements from different points are used to determine unknown distances or positions. Isosceles triangles are also utilized in GPS technology for positioning and mapping.
Physics and Engineering
Isosceles triangles are employed in various physics and engineering applications. They are used to analyze forces and vectors, resolve forces into components, and calculate angles in mechanical systems. Isosceles triangles also find application in optics, fluid mechanics, and electrical circuits.
Geometry Constructions
Isosceles triangles are frequently used in geometric constructions. Their symmetry and specific angle relationships make them valuable tools for constructing perpendicular lines, bisecting angles, and dividing line segments accurately.
Education and Problem Solving
Isosceles triangles are an essential component of mathematics education. They serve as examples for teaching geometry concepts, and problems involving isosceles triangles help develop critical thinking and problem-solving skills.
Nature and Science
Isosceles triangles can be observed in natural phenomena and scientific studies. For instance, the shape of some crystals, such as quartz, exhibits isosceles triangle characteristics. Isosceles triangles are also encountered in the study of waves, optics, and biological structures.
Understanding the applications of the isosceles triangle in various fields highlights its significance and versatility in practical contexts. The unique properties of this geometric shape contribute to its wide-ranging usefulness and make it a fundamental concept in various disciplines.
Exercise
Example 1
Finding an angle
In an isosceles triangle ABC, AB = AC, and ∠BAC = 60 degrees. Find ∠ABC and ∠ACB.
Solution
In an isosceles triangle, the base angles are equal. Therefore, ∠ABC = ∠ACB. Because the sum of angles in a triangle is 180 degrees, we find the base angles as follows:
∠ABC = ∠ACB = (180 – ∠BAC)/2
∠ACB = (180 – 60)/2
∠ACB = 60 degrees.
Example 2
Finding a side length
In an isosceles triangle PQR, PQ = PR = 7 cm, and QR = 10 cm. Find the height from P to QR.
Solution
The altitude splits the base QR into two equal parts. Therefore, each half of the base is 10/2 = 5 cm. Now, we can use the Pythagorean theorem to find the altitude:
P×Q² = (Q×R/2)² + height².
Solving for height, we get
height = √(PQ² – (QR/2)²)
height = √(7² – 5²)
height = √24 cm.
Example 3
Area of an isosceles triangle
Given an isosceles triangle XYZ given in Figure-6, with base XY = 12 cm and height from Z to XY of 8 cm, find the area.
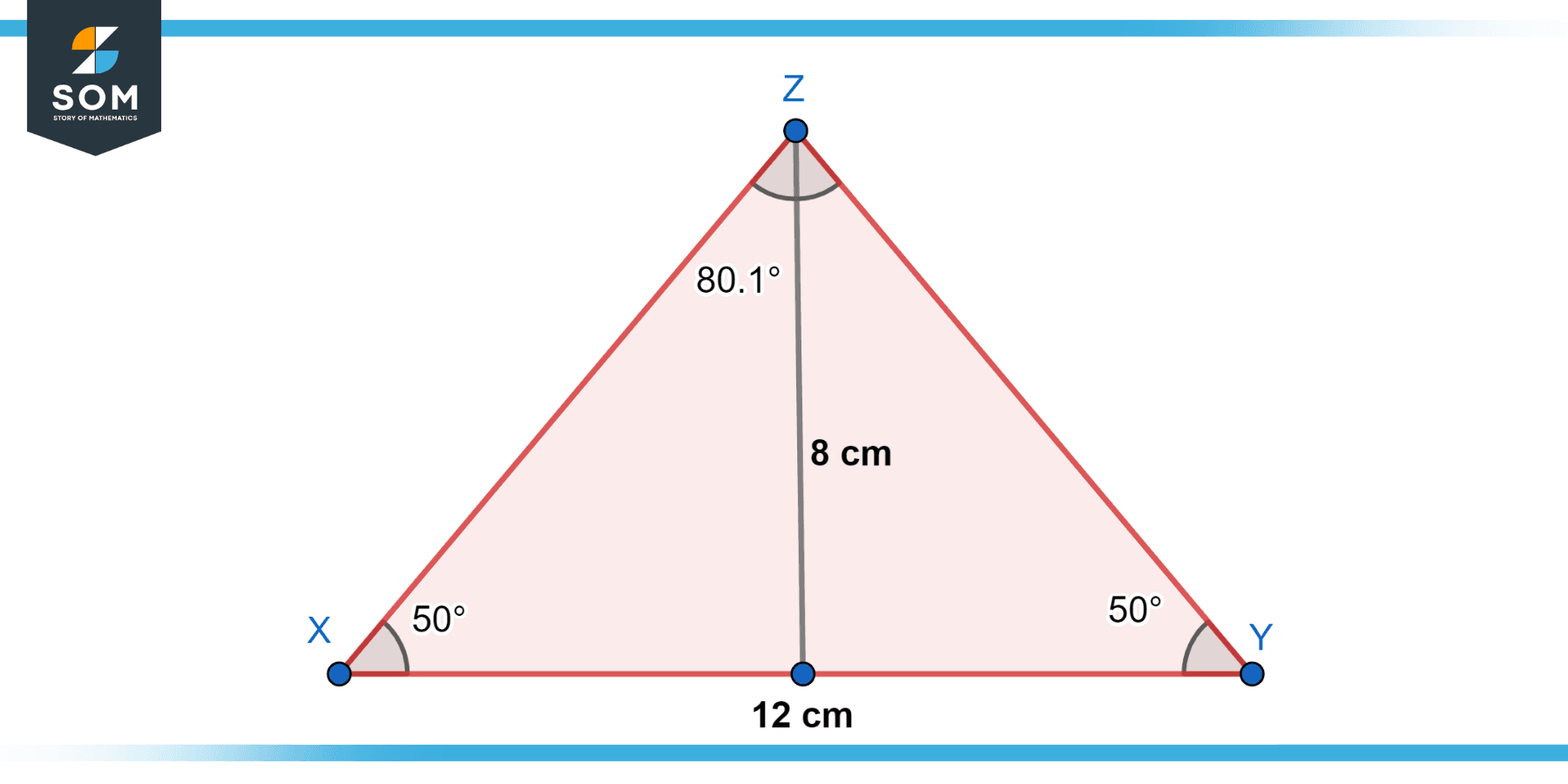
Figure-6.
Solution
The area of a triangle is given by
A = 1/2 × base × height
A = 1/2× 12 ×8
A = 48 cm²
Example 4
Equilateral Triangle
In an isosceles triangle DEF, DE = EF = DF = 10 cm. What are the angles of the triangle?
Solution
This is actually an equilateral triangle, which is a specific type of isosceles triangle. All angles of an equilateral triangle are equal. Therefore:
∠DEF = ∠EDF = ∠EFD = 180/3 = 60 degrees.
Example 5
Finding the base
The perimeter of an isosceles triangle LMN with equal sides of 8 cm each is 24 cm. Find the base LM.
Solution
The perimeter is the sum of all sides, so LM = Perimeter – LN – MN = 24 – 8 – 8 = 8 cm.
Example 6
Right Isosceles Triangle
Given a right isosceles triangle WXY with ∠WXY = 90 degrees and WY = 7√2 cm, find WX and XY.
Solution
In a right isosceles triangle, the hypotenuse is √2 times the length of each leg. Therefore, WX = XY = WY/√2 = 7 cm.
Example 7
Obtuse Isosceles Triangle
In an isosceles triangle, RST, ∠RST = 120 degrees, and RS = ST = 10 cm. Find the length of RT.
Solution
Since the base angles of an isosceles triangle are equal, ∠SRT = ∠STR = (180 – 120)/2 = 30 degrees. RT is the side opposite the 120-degree angle in the triangle, so by the law of cosines;
RT² = RS² + ST² – 2 × RS × ST × cos(120)
RT² = 10² + 10² – 2 × 10 × 10 × (-1/2)
RT² = 200 + 100
RT² = 300
Therefore RT = √300 cm = 10√3 cm.
Example 8
Acute Isosceles Triangle
In an isosceles triangle ABC, ∠BAC = 40 degrees and AB = AC = 12 cm. Find the length of BC.
Solution
Since ∠BAC = 40 degrees, the base angles are ∠ABC = ∠ACB = (180 – 40)/2 = 70 degrees. The length of BC can be found using the law of cosines,;
BC² = AB² + AC² – 2 × AB * AC × cos(40)
BC = √(12² + 12² – 2 × 12 × 12 × cos(40))
BC = √(144 + 144 – 2 × 144 × 0.7660)
BC ≈ √(144 + 144 – 221.184)
BC≈ √(66.816) cm
All images were created with GeoGebra.
