JUMP TO TOPIC
Factoring quadratics is breaking down the factors of a quadratic expression, and since a quadratic expression is a polynomial of degree 2, then a quadratic polynomial has at most two real roots. In factoring a quadratic expression, we have to identify the two factors (of degree 1) that will give the initial quadratic expression when multiplied.
There are different methods that we can use in factoring quadratic expressions. The tricky part is that not every method applies to every quadratic expression, so you must familiarize yourself with each method until you know which one to use in any given quadratics. This article will provide you with a complete guide on using each method and examples so we can apply them.
How to Factor a Quadratic Equation
In factoring a quadratic equation $ax^2+bx+c=0$, you need to solve for the factors $p_1 x+r_1$ and $p_2 x+r_2$ such that:
$$(p_1 x+r_1 )(p_2 x+r_2 )=ax^2+bx+c.$$
For instance, take the quadratic equation:
$$2x^2+3x-2=0.$$
The factors of the given quadratic polynomial are $2x-1$ and $x+2$ because, when multiplied, it will give us the polynomial $2x^2+3x-2$. So we can rewrite the quadratic equation above as
$$(2x-1)(x+2)=0.$$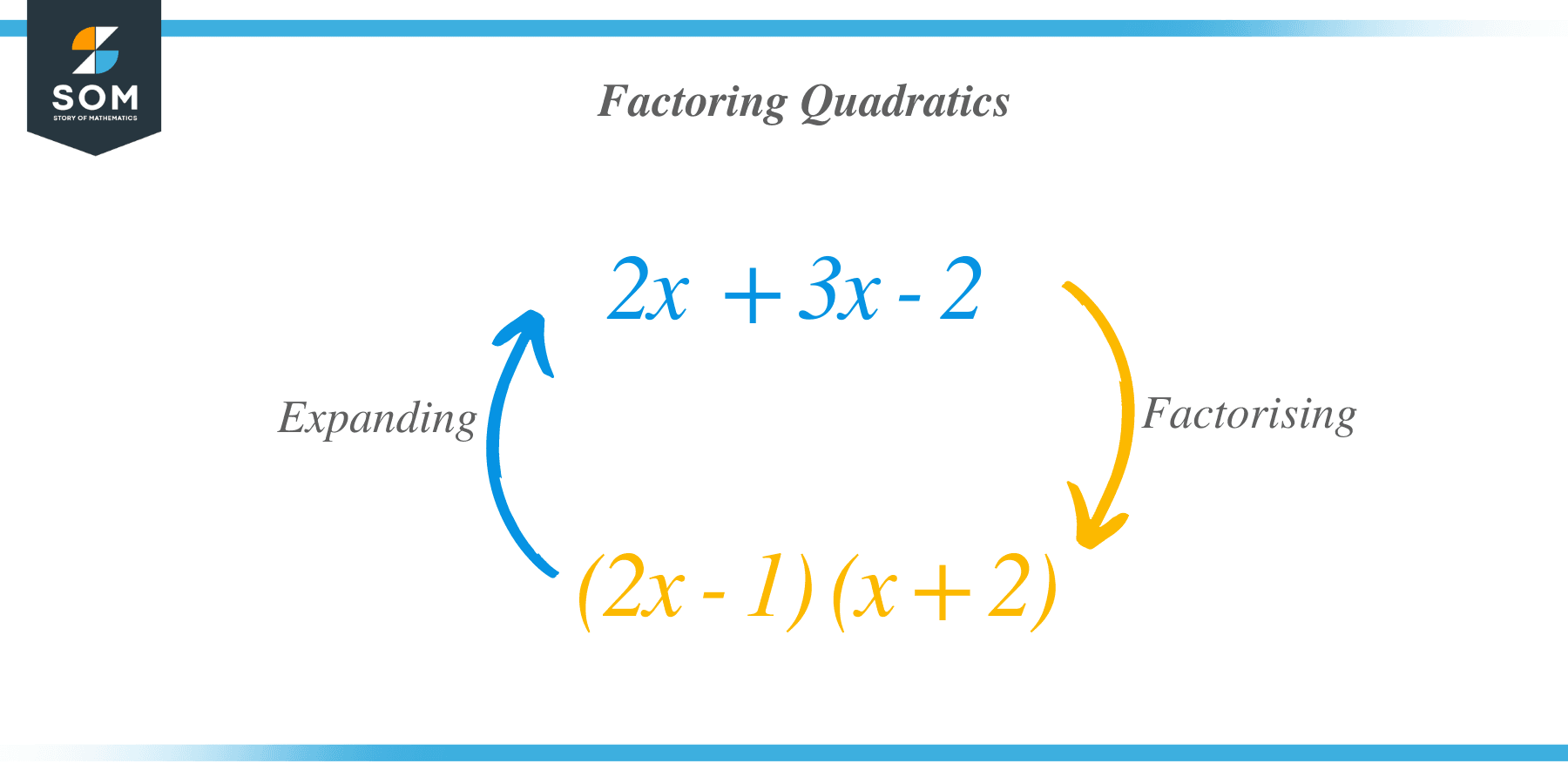
But before you can solve these factors, you must first know which method to use to arrive at the correct factors of a quadratic polynomial. Of course, you cannot go around multiplying every factor you can think of until you arrive at the original quadratic expression.
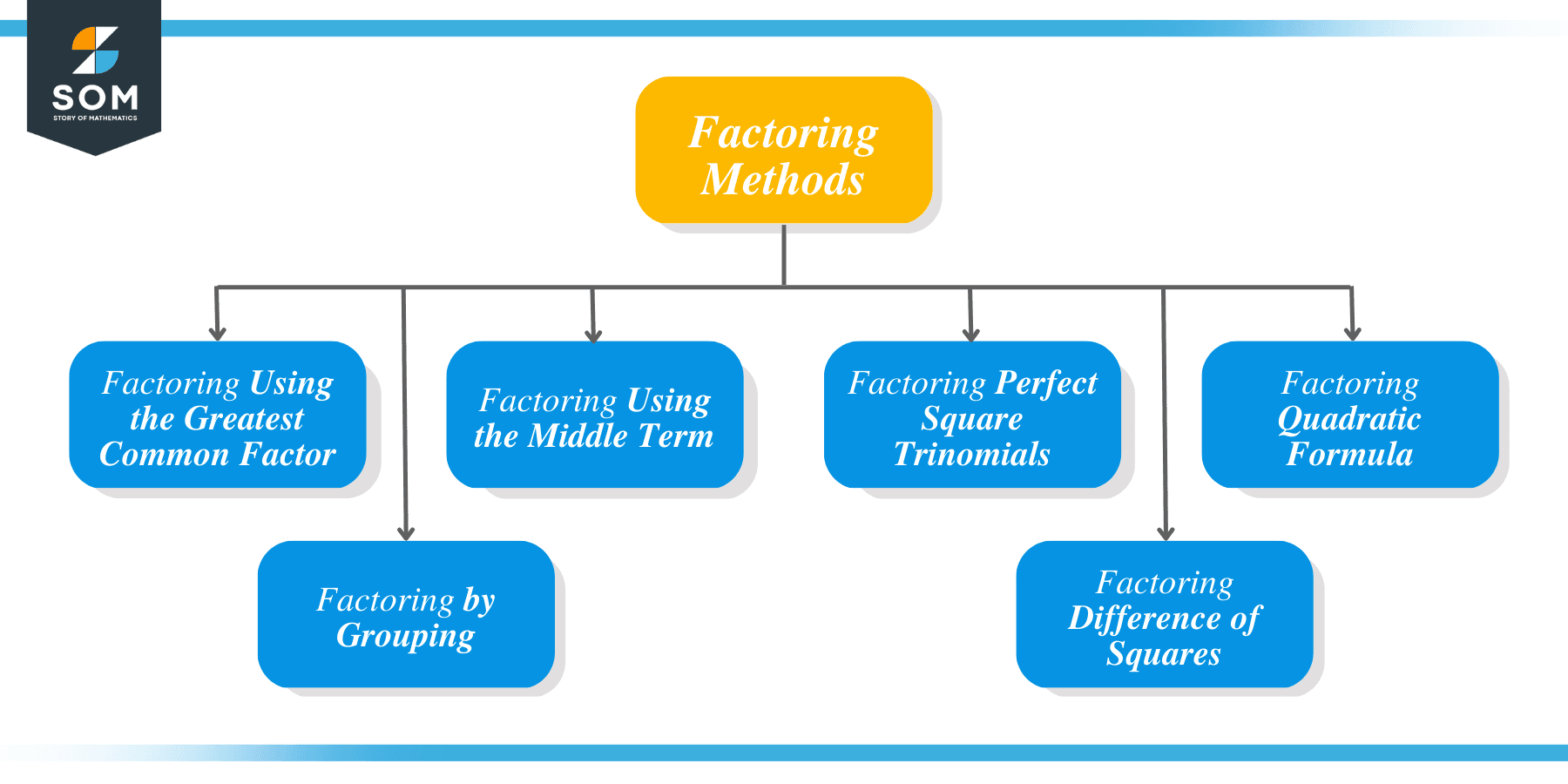
In this article, we exhaust all the possible methods we could use in factoring quadratic expressions. We will discuss the following methods, which quadratic polynomials they apply, and give examples.
- Factoring Using the Greatest Common Factor
- Factoring by Grouping
- Factoring Using the Middle Term
- Factoring Perfect Square Trinomials
- Factoring Difference of Squares
- Factoring Quadratic Formula
Factoring Using the Greatest Common Factor
Some quadratic expressions share a common factor in each term in the expression. The goal is to factor out the greatest factor common to each term.
We are familiar with finding the greatest common factor of two numbers. For example, the greatest common factor of $12$ and $18$ is $6$. This also applies to factoring quadratics that share a common factor.
This method applies to quadratic expressions of the form:
$$ax^2+bx.$$
where $a$ and $b$ share a common factor. If $d$ is the greatest common factor of $a$ and $b$, then we can factor out $d$ on $a$ and $b$ so that we have coefficients $\dfrac{a}{d}$ and $\dfrac{b}{d}$.
$$ax^2+bx=d\left(\dfrac{a}{d} x^2+\dfrac{b}{d} x\right)$$
Note that since $d$ is a factor of $a$ and $b$, we are guaranteed that $\frac{a}{d}$ and $\frac{b}{d}$ are integers. Moreover, we can also factor out $x$ since $x$ is the greatest common factor of $x$ and $x^2$.
Thus, factoring the expression, we have:
$$ax^2+bx=(dx)\left(\dfrac{a}{d}x+\dfrac{b}{d}\right).$$
Let’s look at some of the examples.
Example 1
- Factor the quadratic expression $15x^2-25x$.
We take the coefficients $15$ and $25$ and solve for its greatest common factor. We know that the greatest common factor of $15$ and $25$ is $5$. Thus, we can factor out $5x$ from the expression. So we have:
\begin{align*}
15x^2-25x&=(5x)\left(\dfrac{15x^2}{5x}-\dfrac{25x}{5x}\right)\\
&=(5x)(3x-5).
\end{align*}
Hence, the factors of $15x^2-25x$ are $5x$ and $3x-5$.
- Solve for the factors of $9x^2+2x$.
The coefficients of the quadratic expression are $9$ and $2$. However, $9$ and $2$ do not have a common factor greater than $1$. Thus, the greatest common factor of the coefficients is $1$. This means that we will only factor out $x$ in the expression. So factoring $9x^2+2x$, we have
$9x^2+2x=x(9x+2).$
In Example 1, all the quadratic expressions are factored completely because the factors are of the form $p_1 x+r_1$ and $p_2 x+r_2$, wherein $r_1$ is zero.
For some quadratic expression that is not in the form of $ax^2+bx$, we can still use factoring using the greatest common factors. If all the coefficients of quadratic expression have a common factor, then we can factor out the greatest common factor from the expression. Suppose $d$ is the greatest common factor of $a$, $b$, and $c$. Then we have
$$ax^2+bx+c=d\left(\dfrac{a}{d} x^2+\dfrac{b}{d} x+\dfrac{c}{d}\right).$$
Similarly, we are guaranteed that $\frac{a}{d}$, $\frac{b}{d}$, and $\frac{c}{d}$ are integers because $d$ is a factor common to them. However, in this case, we cannot factor the quadratic expression completely because the remaining expression after factoring out $d$ is still a quadratic expression. So we still need to apply other methods to factor this expression completely.
Factoring by Grouping
If we cannot guarantee that each term of a quadratic expression has a common factor, then sometimes we can group terms that have a common factor so we can factor out something from these grouped terms.
Let $ax^2+bx+c$ be a quadratic expression. If we can find two numbers $j$ and $k$ such that
\begin{align*}
j+k&=b\\
jk&=ac,
\end{align*}
then we can group each of the terms $ax^2$ and $c$ with the coefficients $j$ and $k$ such that both groupings will have a common factor.
\begin{align*}
ax^2+bx+c&=ax^2+(j+k)x+c\\
&=(ax^2+jx)+(kx+c).
\end{align*}
We can factor out the greatest common factor for each grouping until you have something like this:
\begin{align*}
ax^2+bx+c&=mx(px+q)+n(px+q)\\
&=(mx+n)(px+q).
\end{align*}
Then the factors of $ax^2+bx+c$ are $mx+n$ and $px+q$.
Let’s look at some more examples to apply this method.
Example 2
- Factor completely the quadratic expression $3x^2+10x+8$.
The coefficient of the middle term is $10$ and the product of the first and last term is $3\times8=24$. So you first look for possible pairs that will give you a sum of $10$, then check if the product is equal to $24$.
Note that $4+6=10$ and $4\times6=24$. Thus, we have the pair $4$ and $10$. So we rewrite the expression so we can group them later.
$$3x^2+10x+8=3x^2+(4x+6x)+8$$
We group the terms that have a common factor, so we group $6x$ with $3x^2$, and $4x$ with $8$, then factor out their respective common factors.
\begin{align*}
3x^2+10x+8&=(3x^2+6x)+(4x+8)\\
&=3x(x+2)+4(x+2)\\
&=(3x+4)(x+2).
\end{align*}
Thus, the factors of $3x^2+10x+8$ are $3x+4$ and $x+2$.
- Find the factors of the quadratic equation $10x^2+11x-6=0$.
The product of the first and last term is a negative number, $10\times(-6)=-60$. So we are looking for factors of $-60$, a positive number and a negative number, that will give us a sum of $11$.
Note that the sum of $15$ and $-4$ is $11$, and the product of these numbers is $-60$. So we have:
\begin{align*}
10x^2+11x-6&=0\\
10x^2+15x-4x-6&=0
\end{align*}
We can group $15x$ and $-4x$ with either $10x^2$ and $-6$ since each grouping has a common factor. So you can choose whichever and you will still arrive at the same factors.
\begin{align*}
(10x^2+15x)+(-4x-6)&=0\\
5x(2x+3)-2(2x+3)&=0\\
(5x-2)(2x+3)&=0
\end{align*}
Therefore, we have factored the quadratic equation completely.
Factoring Using the Middle Term
This method is similar to the grouping method applied to simpler forms of a quadratic expression. Suppose we have a quadratic expression with no coefficient on the first term:
$$x^2+bx+c.$$
We look at the coefficient of the middle term and find two numbers, $u$ and $v$, that when added will give us $b$ and will give us a product $c$. That is:
\begin{align*}
u+v&=b\\
uv&=c
\end{align*}
So that when we can express the quadratic polynomial as:
\begin{align*}
x^2+bx+c&=x^2+(u+v)x+(uv)\\
&=(x+u)(x+v).
\end{align*}
Let’s apply this method in the following examples.
Example 3
- Solve for the factors of $x^2-7x+12$.
Since the middle term has a negative sign while the last term has a positive sign, then we are looking for two negative numbers that will give us a sum of $-7$ and a product of $12$.
The possible factors of $12$ are $-1$ and $-12$, $-2$ and $-6$, and $-3$ and $-4$. The only pair that will give us a sum of $-7$ is $-3$ and $-4$. Thus, we can factor the expression into
$$x^2-7x+12=(x-3)(x-4).$$
- Factor completely the equation $x^2-2x-24=0$.
The last term has a negative sign, thus, we are looking for a positive number and a negative number. Note that the product of $-6$ and $4$ is $-24$ and their sum is $-2$. Thus, we can factor the equation as:
\begin{align*}
x^2-2x-24&=0\\
(x-6)(x+4)&=0
\end{align*}
Factoring Perfect Square Trinomials
A perfect square trinomial is a quadratic polynomial that has only one distinct factor with multiplicity $2$.
To determine if a quadratic polynomial is a perfect square, the first and last terms must be perfect squares. That is:
$$ax^2=(mx)^2,$$
and:
$$c=n^2.$$
Next, you need to check for the middle term if it is twice the product of the roots of the first and last term.
$$bx=2mnx.$$
If these conditions are satisfied, then you have a perfect square trinomial that can be factored completely as:
$$ax^2+bx+c=(mx+n)^2.$$
Take note that the first and last terms both have positive signs. So if the middle term is positive, the operation of the factor is addition, and if the middle term is negative, the operation of the factor is subtraction.
Example 4
| Perfect Square Trinomials | Checking | Factoring |
|---|---|---|
| $x^2+12x+36$ | $(x)^2+2(x)(6)+(6)^2$ | $(x+6)^2$ |
| $4x^2-20x+25$ | $(2x)^2-2(2x)(5)+(5)^2$ | $(2x-5)^2$ |
| $49x^2+56x+16$ | $(7x)^2+2(7x)(4)+(4)^2$ | $(7x+4)^2$ |
Factoring Difference of Two Squares
A quadratic expression that is of the form of difference of two squares can be factored as:
$$a^2 x^2-c^2=(ax+c)(ax-c).$$
The factors are always the sum and difference of the roots. This holds true because if we take the product of the factors, the middle term becomes zero because of the opposing signs.
\begin{align*}
(ax+c)(ax-c)&=(ax)^2+acx-acx-c^2\\
&=a^2 x^2-c^2
\end{align*}
Example 5
| Difference of Squares | Expanding | Factoring |
|---|---|---|
| $x^2-9$ | $(x)^2-(3)^2$ | $(x+3)(x-3)$ |
| $100x^2-81$ | $(10x)^2-(9)^2$ | $(10x+9)(10x-9)$ |
| $49-16x^2$ | $(7)^2-(4x)^2$ | $(7+4x)(7-4x)$ |
Factoring Quadratic Formula
When you have tried all the methods and you still cannot find the factors of the quadratic expression, you can always use the quadratic formula. For the quadratic expression $ax^2+bx+c$, the quadratic formula is given by:
$$r_{1,2}=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}.$$
Note that the quadratic formula will give us two roots, $r_1$ and $r_2$, because subtraction and addition will be performed in the numerator. Then the resulting factors are $x-r_1$ and $x-r_2$.
This is because the quadratic formula simplifies the expression into
$$\dfrac{ax^2+bx+c}{a}=x^2+\dfrac{b}{a} x+\dfrac{c}{a}.$$
Thus, if $a>1$, then multiply $a$ to one of the factors.
Example 6
- Factor the expression $x^2+4x-21$ using the quadratic formula.
From the expression, we have $a=1$, $b=4$, and $c=-21$. Substituting these values in the quadratic formula, we have:
\begin{align*}
r&=\dfrac{-4\pm\sqrt{(4)^2-4(1)(-21)}}{2(1)}\\
&=\dfrac{-4\pm\sqrt{16+84}}{2}\\
&=\dfrac{-4\pm\sqrt{100}}{2}\\
&=\dfrac{-4\pm10}{2}.
\end{align*}
So we have the roots:
$$r_1=\dfrac{-4+10}{2}=\dfrac{6}{2}=3$$
and:
$$r_2\dfrac{-4-10}{2}=\frac{-14}{2}=-7.$$
Thus, the factors are $x-3$ and $x-(-7)=x+7$.
$$x^2+4x-21=(x-3)(x+7)$$
- Factor completely the equation $2x^2+5x-3$ using the quadratic formula.
Note that $a=2$, $b=5$, and $c=-3$. Plugging in these values in the quadratic formula, we have
\begin{align*}
r&=\dfrac{-5\pm\sqrt{5^2-4(2)(-3)}}{2(2)}\\
&=\dfrac{-5\pm\sqrt{25+24x}}{4}\\
&=\dfrac{-5\pm\sqrt{49}}{4}\\
&=\dfrac{-5\pm7}{4}.
\end{align*}
We have the roots:
$$r_1=\dfrac{-5+7}{4}=\dfrac{2}{4}=\dfrac{1}{2}$$
and:
$$r_2=\dfrac{-5-7}{4}=\dfrac{-14}{4}=-7.$$
From this, we have the factors $x-1/2$ and $x-(-7)=x+7$.
However, since $a=2$, we multiply $2$ to the factor $x-1/2$.
$$2\left(x-\dfrac{1}{2}\right)=2x-1.$$
Thus, we factor the expression as
$$2x^2+5x-3=(2x-1)(x+7).$$
We can use the quadratic formula for any quadratic expression, but the roots that we will get are not always guaranteed to be an integer. Moreover, when $b^2-4ac$ is negative, then we have no real roots, so we cannot factor the quadratic expression.
Conclusion
We have discussed all the methods you can use in factoring quadratics, and we have also shown how these methods are derived, how and when to use them, and how to apply them in the examples. Let’s summarize our discussion on factoring quadratics in the following table.
| Quadratic Expression: $ax^2+bx+c$ | |||
|---|---|---|---|
| Method | When to use them | Expression | Factors |
| Greatest Common Factor | When there is no last term, and $a$ and $b$ have a common factor | $ax^2+bx$ | $(dx)\left(\dfrac{a}{d} x+\dfrac{b}{d}\right)$ |
| Grouping Method | When the sum of two numbers is $b$ and their product is equal to $ac$ | $(ax^2+jx)+(kx+c)$ | $(mx+n)(px+q)$ |
| Using the Middle Term | When $a=1$, and the sum of two numbers is $b$ and the product is $c$ | $x^2+(u+v)x+uv$ | $(x+u)(x+v)$ |
| Perfect Square Trinomials | When the first and last terms are perfect squares and the middle term is twice the product of the roots | $(ax)^2+2abx+(b)^2$ | $(ax+b)^2$ |
| Difference of Two Squares | When there is no middle term, and the form is the difference of the first and last term | $(ax)^2-c^2$ | $(ax+c)(ax-c)$ |
| Quadratic Formula | Any quadratic expression | $r_{1,2}=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$ | $(x-r_1 )(x-r_2 )$ |
Some forms of a quadratic expression apply to more than one method, but the goal here is to factor the quadratics completely, so you need to try which method is appropriate for the expression and which you find easier to use. It takes constant practice to know which method to use right away, but once you are familiar with these methods, you can easily (and sometimes mentally) factor quadratic expressions.