JUMP TO TOPIC
The glide reflection is a great example of a composite transformation, which means it is composed of two basic transformations. Through glide reflection, it is now possible to study the effects of combining two rigid transformations as well. To provide an analogy: imagine walking barefoot on the beach, the footprints formed exhibit glide reflection.
The glide reflection combines two fundamental transformations: reflection and translation. The resulting change on the pre-image reflects an image that seems to have a “gliding effect,” hence the name of this transformation.
This article covers the fundamentals of glide reflections (this includes a refresher on translation and reflection). It covers how the order of transformations affects the glide reflection as well as the rigidity of glide reflection. By the end of the discussion, glide reflection is going to be an easy transformation to apply in the future!
What Is a Glide Reflection?
A glide reflection is the figure that occurs when a pre-image is reflected over a line of reflection then translated in a horizontal or vertical direction (or even a combination of both) to form the new image.
This means that the glide reflection is also a rigid transformation and is the result of combining the two core transformations: reflection and translation.
- Reflection is a basic transformation that flips over the pre-image with respect to a line of reflection to project the new image.
- Translation is another rigid transformation that “slides” through a pre-image to project the desired image.
The glide reflection does all two in no specific order. To better understand how the glide reflection works, take a look at the illustration shown below.
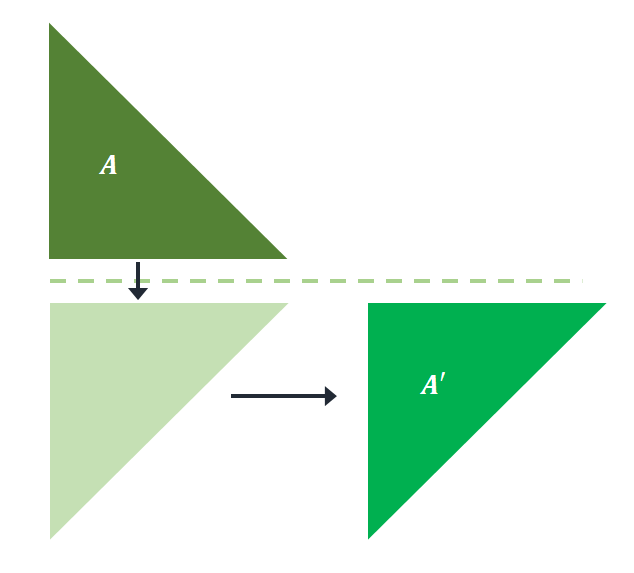
The pre-image, $A$, is reflected over the horizontal line. The projected shape is then translated into a few units to the right to construct $A^{\prime}$. This means that a glide reflection was performed for $A$ to project the image $A^{\prime}$.
As mentioned, translating the pre-image first before reflecting it over will still return the same image in glide reflection. If $A$ is first translated to the right and then reflected over the horizontal line, the same image is projected over $A^{\prime}$.
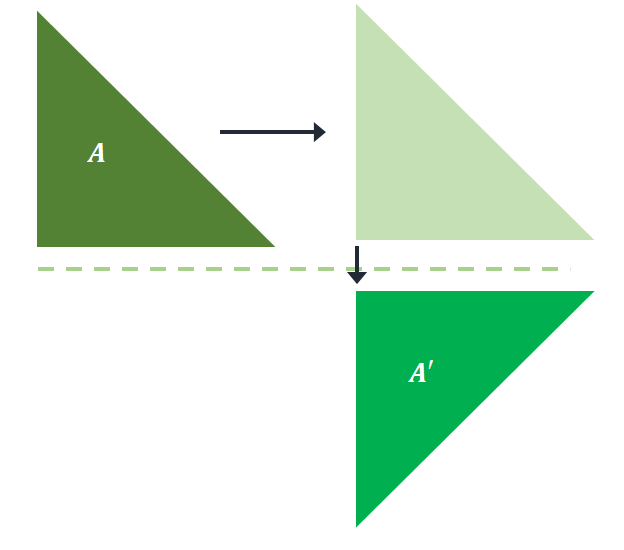
This confirms that glide reflection requires no order for its transformation. Since only the position and orientation have changed, glide reflection can also be classified as a rigid transformation.
In glide reflection, the size and shape of the pre-image remain the same for the resulting image. The next section breaks down the steps to implement glide reflection on different objects.
How To Do a Glide Reflection?
To do a glide reflection, perform the two transformations, which are 1) reflection over the given line of reflection and 2) translation with respect to the given directions. This means that to master glide reflection, it is important to master the two basic transformations.
There are instances when reflecting the pre-image is much more convenient before translating it or vice-versa. Take advantage of the fact that in glide reflection, the order does not matter. For now, it’s important to take a quick refresher on the process of translating and reflecting pre-images.
Translation
This covers both vertical and horizontal translations. When performing translations, “slide” the object from along the $x$-axis or $y$-axis depending on the type of translation being done.
Here’s a quick guide on all possible translations that can be applied on a pre-image located on an $xy$-plane.
Horizontal Translation | $h$ units to the right | $(x, y) \rightarrow (x + h, y)$ |
$h$ units to the left | $(x, y) \rightarrow (x – h, y)$ | |
Vertical Translation | $k$ units upward | $(x, y) \rightarrow (x, y + k)$ |
$k$ units downward | $(x, y) \rightarrow (x, y – k)$ | |
Combined Translation | $h$ units to the right, $k$ units upward | $(x, y) \rightarrow (x +h, y + k)$ |
$h$ units to the left, $k$ units downward | $(x, y) \rightarrow (x -h, y – k)$ | |
$h$ units to the right, $k$ units downward | $(x, y) \rightarrow (x +h, y – k)$ | |
$h$ units to the left, $k$ units upward | $(x, y) \rightarrow (x – h, y + k)$ |
Suppose that a triangle, $\Delta ABC$, has the following vertices on the coordinate system: $A = (2, 1)$, $B = (8, 5)$, and $C = (8, 1)$. With the help of the guide, translate the triangle $3$ units to the left and $5$ units downward.
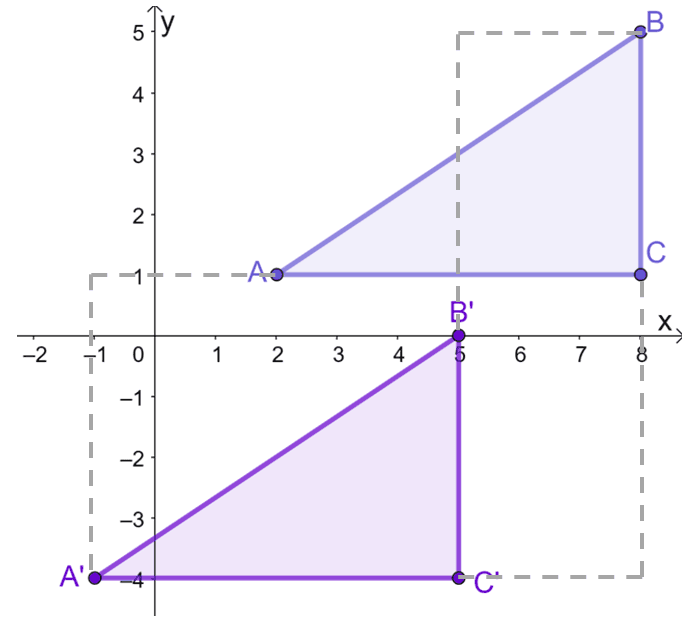
After graphing $\Delta ABC$ on the $xy$-plane, translate each point or vertex $3$ units to the left and $5$ units downward. This can be done graphically or by working on the coordinates of $\Delta ABC$.
\begin{aligned}A \rightarrow A^{\prime}\end{aligned} | \begin{aligned}B \rightarrow B^{\prime}\end{aligned} | \begin{aligned}C \rightarrow C^{\prime}\end{aligned} |
\begin{aligned}A^{\prime} = (2 – 3, 1 – 5)\\&= (-1, -4)\end{aligned} | \begin{aligned}B^{\prime} = (8 – 3, 5 – 5)\\&= (5, 0)\end{aligned} | \begin{aligned}C^{\prime} = (8 – 3, 1 – 5)\\&= (5, -4)\end{aligned} |
This means that after both vertical and horizontal translations, the vertices of the resulting image $\Delta A^{\prime}B^{\prime}C^{\prime}$ are $(-1, -4)$, $(5, 0)$, and $(5, -4)$.
Reflection
When reflecting a point or an object, reflect it over the line of reflection. The common lines of reflections are 1) the $x$-axis, 2) the $y$-axis, 3) the line $y = x$, and 4) the line $y = -x$.
Use the guide below when reflecting objects.
Reflection over the $x$-axis | \begin{aligned}(x, y) \rightarrow (x, -y) \end{aligned} |
Reflection over the $y$-axis | \begin{aligned}(x, y) \rightarrow (-x, y) \end{aligned} |
Reflection over $y =x$ | \begin{aligned}(x, y) \rightarrow (y, x) \end{aligned} |
Reflection over $y = -x$ | \begin{aligned}(x, y) \rightarrow (-y, -x) \end{aligned} |
Now, using the resulting triangle $\Delta A^{\prime}B^{\prime}C^{\prime}$, reflect it over the $y$-axis. There are two ways to do this: construct the line $x = 0$ then reflect each vertex over or apply the coordinate rules shown above. This should lead to the image shown below.
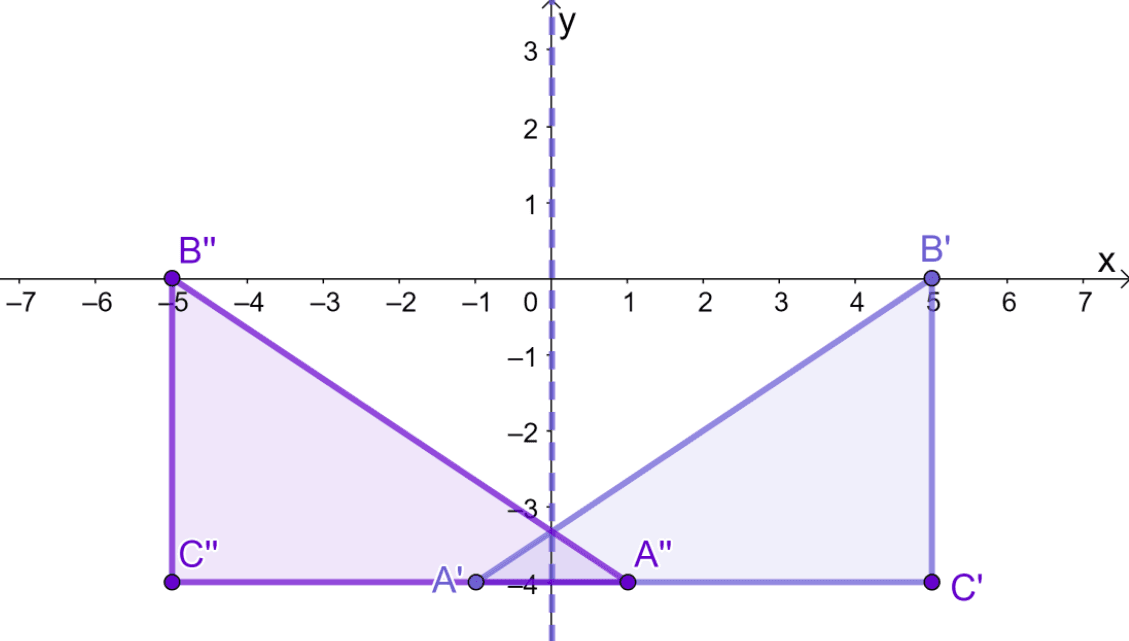
This means that after reflecting $\Delta A^{\prime} B^{\prime} C^{\prime}$ over the the $y$-axis, the resulting triangle will have the following vertices:
\begin{aligned}A^{\prime} = (-1, -4) &\rightarrow A^{\prime\prime} = (1, -4)\\B^{\prime} = (5, 0) &\rightarrow B^{\prime\prime} = (-5, 0)\\C^{\prime} = (5, -4) &\rightarrow C^{\prime\prime} = (-5, -4) \end{aligned}
Now, combining the two processes, $\Delta A^{\prime\prime } B^{\prime\prime } C^{\prime\prime }$ is the result after performing a glide reflection on $\Delta ABC$.
- Horizontal and vertical translation of $-3$ and $-5$ units, respectively.
- Reflection over the $y$-axis.
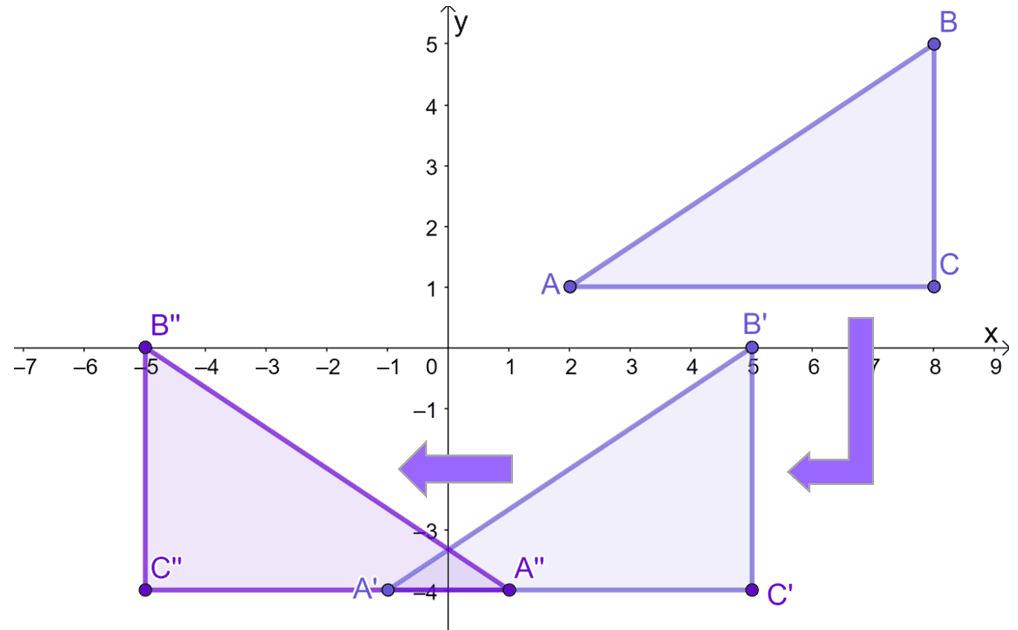
Retracing the steps performed on $\Delta ABC$, the glide reflection performed on pre-image can be summarized by the steps below:
\begin{aligned}\Delta ABC &: (x, y)\\&\downarrow \\\Delta A^{\prime}B^{\prime}C^{\prime}&: (x {\color{Teal}- 3}, y{\color{Teal} -5})\\\downarrow \\\Delta A^{\prime\prime}B^{\prime\prime}C^{\prime\prime}&: ({\color{Teal}-(x – 3)}, y-5)\\&:(-x – 3, y-5)\end{aligned}
The graph shown above also reflects these changes and highlights how the glide reflection has affected the original object, $\Delta ABC$.
It’s time to try out more examples involving glide reflections, so head over to the section below!
Example 1
Suppose that the triangle $\Delta ABC$ is graphed on the $xy$-plane with the following vertices: $A = (-7, 1)$, $B = (1, 5)$, and $C =(1, 1)$. What is the resulting image of $\Delta ABC$ after it is projected through a glide reflection?
- Translation: Move $12$ units to the left.
- Reflection: Reflection over the $x$-axis.
Solution
When working with glide reflection, expect to translate and reflect the given pre-image. Now, graph $\Delta ABC$ on the $xy$-coordinate plane and apply the appropriate transformations:
- Subtract $12$ units from each of $\Delta ABC$’s $x$-coordinate.
\begin{aligned}(x, y) \rightarrow (x – 12, y)\end{aligned}
- Reflect the resulting image over the $x$-axis (represented by $y = 0$), so multiply the $y$-coordinate by $-1$.
\begin{aligned}(x – 12, y) \rightarrow (x – 12, -y)\end{aligned}
This means the transformation $(x, y)\rightarrow (x- 12, -y)$ summarizes the effect of the glide reflection on $\Delta ABC$.
\begin{aligned}A \rightarrow A^{\prime} &=(-7 -12, -1(-1))\\&= (-19, -2)\\B \rightarrow B^{\prime} &=(1 -12, -1(5))\\&= (-11, -5)\\C \rightarrow C^{\prime} &=(1 -12, -1(1))\\&= (-11, -1)\end{aligned}
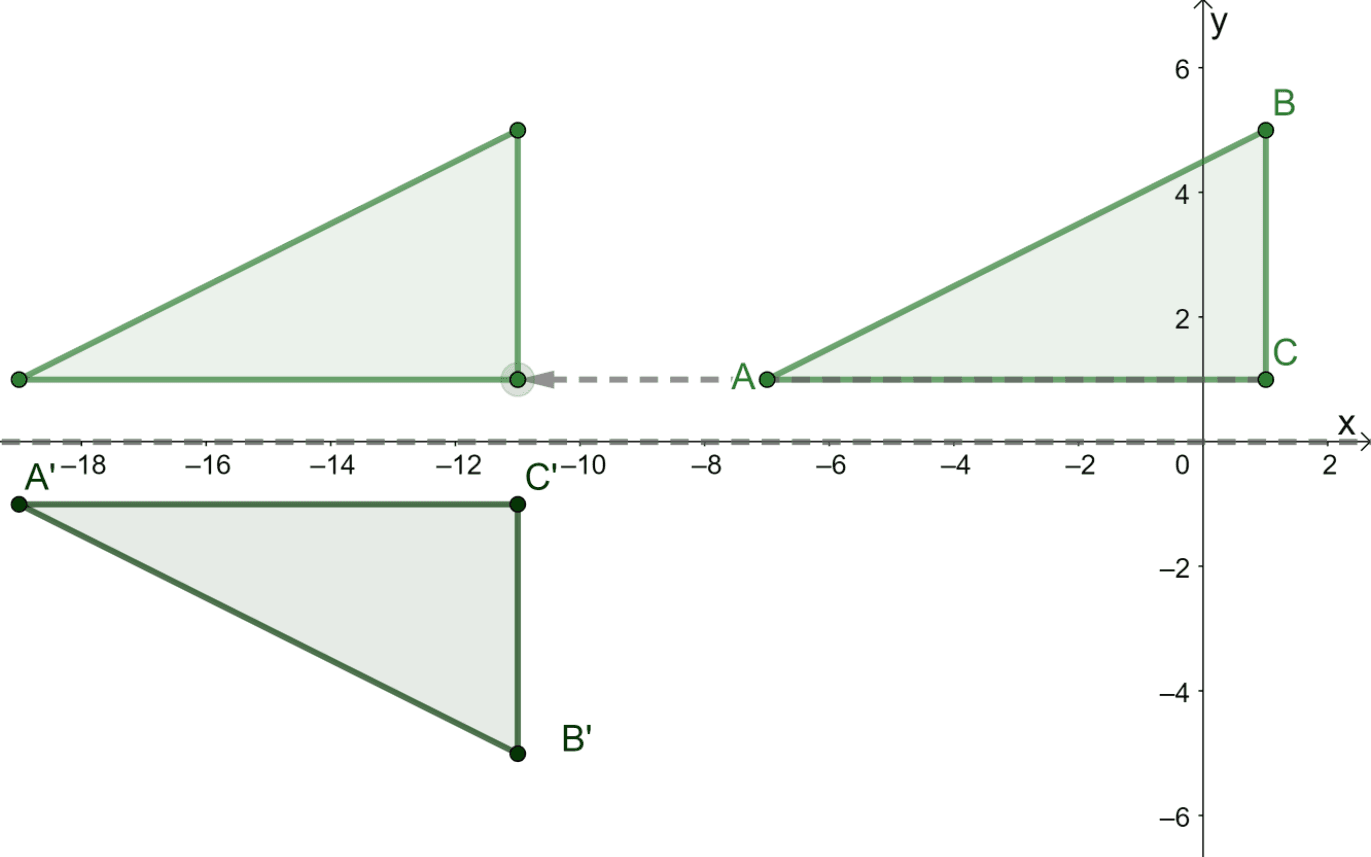
The graph above shows the resulting image of $\Delta A^{\prime}B^{\prime}C^{\prime}$ after the glide reflection.
Practice Question
1. Suppose that the triangle $\Delta ABC$ is graphed on the $xy$-plane with the following vertices: $A = (0, 2)$, $B = (6, 6)$, and $C =(6, 2)$. What is the resulting image of $\Delta ABC$ after it is projected through a glide reflection?
- Translation: Move $6$ units downward
- Reflection: Reflection over the $y$-axis
Which of the following shows the vertices of $\Delta A^{\prime}B^{\prime}C^{\prime}$?
A. $A^{\prime} = (-4, 0)$, $B^{\prime} = (0, -6)$, $C^{\prime} = (-4, -6)$
B. $A^{\prime} = (0, -4)$, $B^{\prime} = (6, 0)$, $C^{\prime} = (-6, -4)$
C. $A^{\prime} = (0, -4)$, $B^{\prime} = (-6, 0)$, $C^{\prime} = (-6, -4)$
D. $A^{\prime} = (0, 4)$, $B^{\prime} = (6, 0)$, $C^{\prime} = (6, 4)$
Answer Key
1. C
Some images/mathematical drawings are created with GeoGebra.
