JUMP TO TOPIC
 If we draw a vertical line in a plane, all the points on one side of the line will make a half-plane.
If we draw a vertical line in a plane, all the points on one side of the line will make a half-plane.
Whenever we draw a straight line in the coordinate plane, it will divide the plane into two halves, and if we take all the points on one side, then the set of those points is known as half-plane.
This guide will help you understand the concept of half-plane, and we will discuss multiple examples along with graphs so you can grasp the idea quickly and easily.
What Is a Half Plane?
The half-plane or semi-plane is all the points on one side of a plane. The upper semi or half-plane is that part of the plane that consists of the points that lie in the 1st and 2nd quadrants. The lower semi or half-plane is that part of the plane that consists of the points that lie in the 3rd and 4th quadrants.
Parts of a Plane
To understand the concept of a half-plane, we should first try to understand the meaning of a plane. A plane is a two-dimensional geometrical object that consists of four quadrants with an infinite number of points. We can use this to draw graphs for linear and non-linear equations and functions. The picture of a simple plane is given below.
If we mark out certain points in the plane and join them, it will give us a graph or line, and by using that, we can formulate an equation of a line, slope, and many other mathematical or geometrical quantities. As we can see, the plane is divided into two semi-planes, the upper semi-plane, and the lower semi-plane.
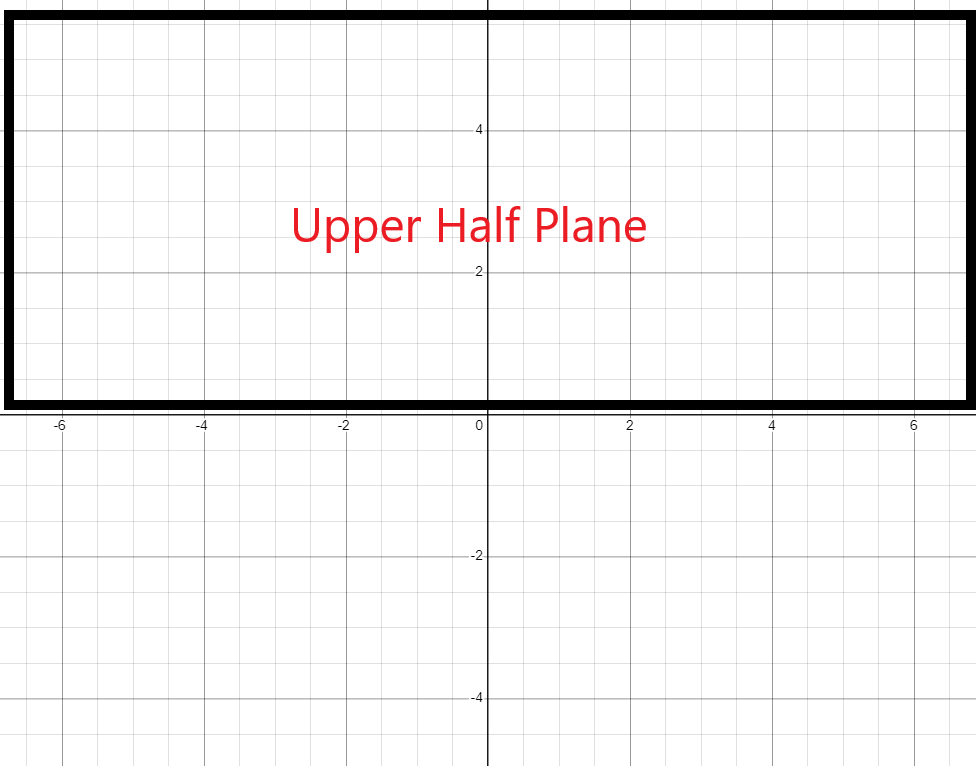
Upper Half-Plane: The upper semi or half-plane is that part of the plane that consists of the points that lie in the 1st and 2nd quadrants of the plane. In the upper half of the plane, the value of the y-coordinate will always remain positive. The name upper half/semi-plane was suggested by the mathematician Poincare, also known as Poincare half-plane.
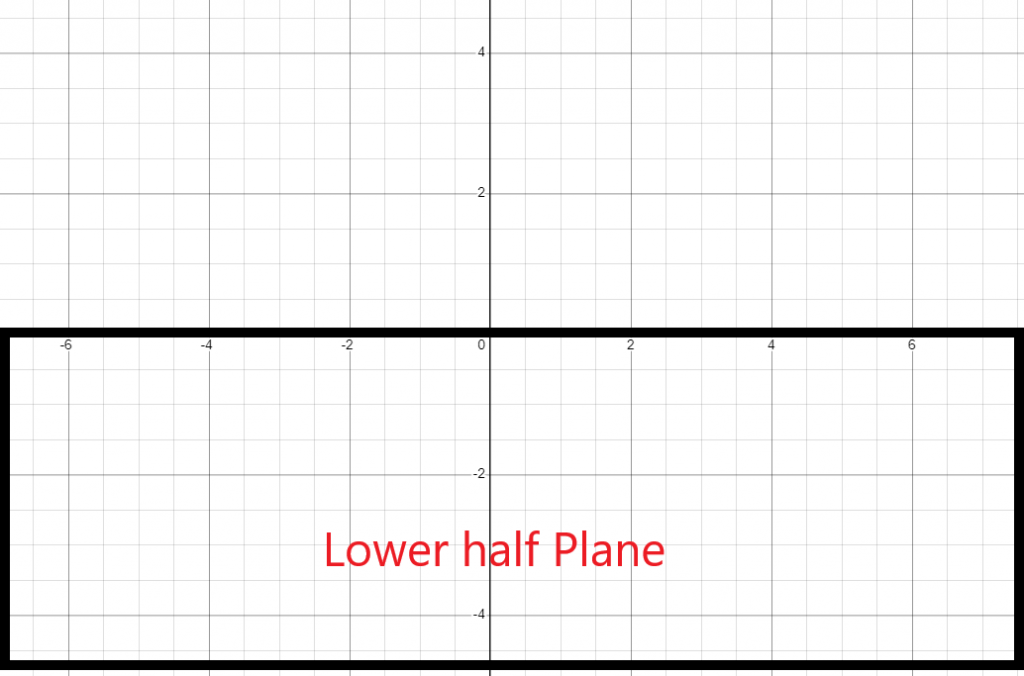
Lower Half-Plane: The lower semi or half-plane is that part of the plane that consists of the points that lie in the 3rd and 4th quadrants of the plane. So, in the lower half of the plane, the value of the y-coordinate will always remain negative.
Types of Half Plane
If plotted on a plane, the linear equations or straight lines divide the plane into two portions; hence we can say that the straight lines form a half-plane, and according to geometry, we can say that the pair of half-planes created by the line will contain an infinite number of points. The line will determine the point’s location, whether the points are on the line or on one side of the plane or the other.
We can use a straight line to determine the type of half-plane. There are two types of half-planes
a) Open half-plane
b) Closed half-plane
Open half-plane definition: The open semi/half-plane is that part of the plane that consists of the points or their intersections on the one side of the straight line, but the catch is that we will not include points of the line or the line itself in the plane. Hence, it is called the open semi plane. The line in the open half-plane is shown as a dotted line below.
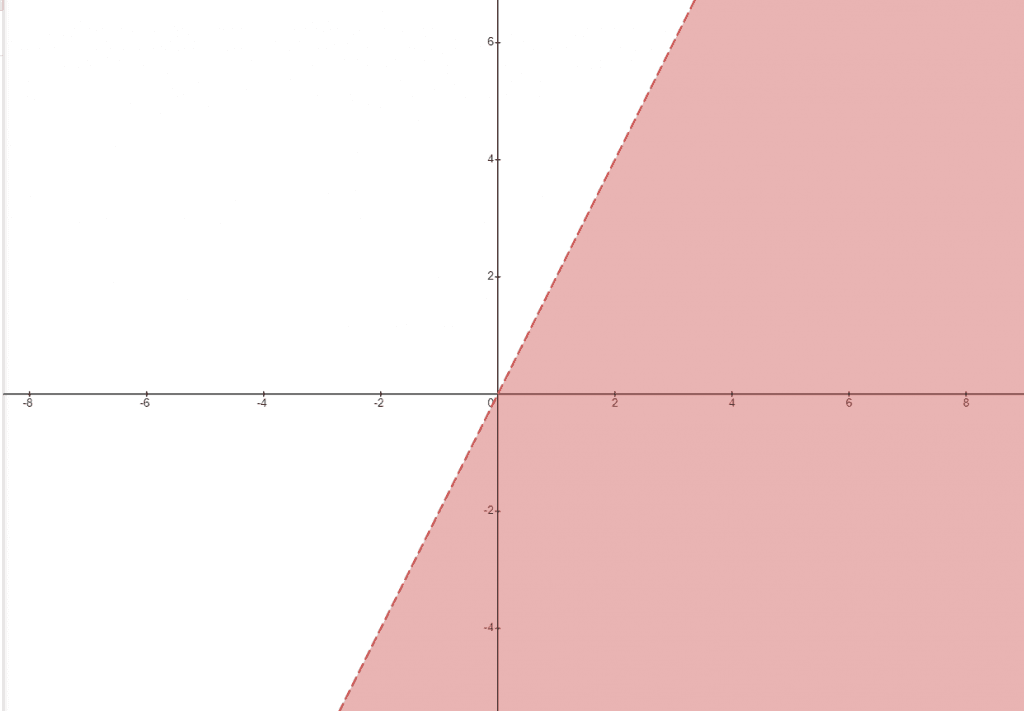
Closed Half-Plane definition: The closed semi/half-plane is a counterpart to the open semi-plane. A closed semi/half-plane is that part of the plane that consists of the points or their intersections on the one side of the straight line, while it also includes the line or the points on the line as well. Hence, it is called the closed semi/half-plane.

So, we can say that any point in the plane will either lie in the open half-plane or on the line itself. The line that divides the plane will be called the division line. If two points lie in different semi planes and we proceed to join them to form a line, then it will intersect the existing division line and form two new semi planes. Let us now study the half-plane and its importance in representing linear inequalities.
Half Plane and Linear Inequalities
Whenever we plot a line in a Cartesian plane, it will divide the plane into two half halves with infinite points. This line is called the division or boundary line. Any linear inequality function or equation graph will always divide the plane into two halves. The linear inequality will either give us a closed half-plane or an open half-plane depending on the type of inequality equation.
Linear inequality and open half-plane: The open semi/half-plane does not include the line, so whenever a linear inequality with a “>” or “<” sign is given, it will always lead to an open half/semi plane.
Linear inequality and open half-plane: The closed semi/half-plane include the boundary or division line, so whenever a linear inequality with “$\geq$” or “$\leq$” sign is given, it will always lead to a closed half/semi plane.
Let us discuss half-plane examples using the half-plane equation and half-plane graph.
Example 1: Draw the graph for the half-plane inequality equation $y < x – 4$. Also, shade the open semi-half of the plane.
Solution:
First, we draw the line by eliminating the inequality sign and write the equation as $y = x – 4$. We can draw the graph for $y = x – 4$ by determining the intersection points.
x | y |
| $-4$ | $-8$ |
$0$ | $-4$ |
| $4$ | $0$ |
$5$ | $1$ |
| $8$ | $4$ |
We can draw the graph by using the above coordinates.
We know that the equation has a “<” sign in it, so the plane formed by the graph will be an open semi-plane and it will not include the boundary line. But one pressing question remains: which side of the line we should shade?
We can easily determine the answer to this question by putting $(0,0)$ in the equation and observing whether or not it satisfies the region we shaded. Let’s assume we shade the right-sided region of the line, and now we want to verify whether it is correct or not.
If we put $x = 0$ and $y = 0$, then inequality equation can be written as:
0 < 0 – 4, so this is incorrect or untrue, so we will shade the region which does not contain $(0,0)$. Hence, our initial assumption was correct. So, to determine which side of the line is to be shaded, we just put $(0,0)$ in the inequality equation to see whether or not it satisfies the equation.
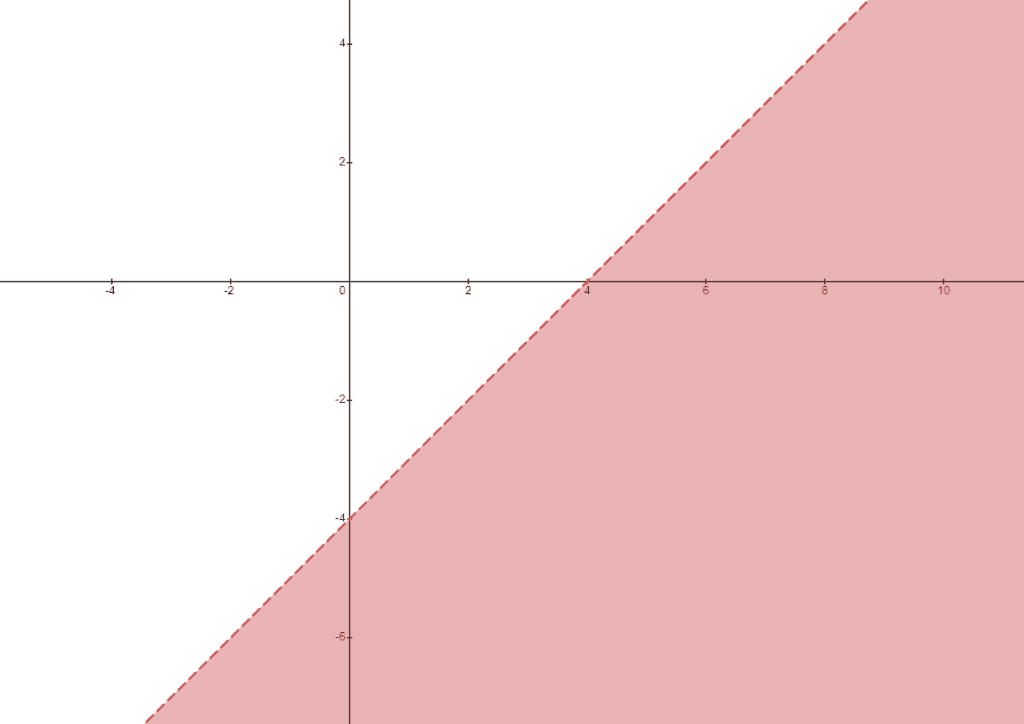
Example 2: Draw the graph for the equation $y < x + 4$. Also, shade the open semi-half of the plane.
Solution:
This example is similar to the previous example, but the only difference is the significant change in the equation. We will follow the same steps as before. We will eliminate the inequality sign and plot the points by using the equation $y = x + 4$.
x | y |
$-8$ | $-4$ |
| $-4$ | $0$ |
| $2$ | $6$ |
| $4$ | $8$ |
We can draw the graph by using the above intersection points.

Let us put $(0,0)$ in the equation to determine which side of the line is to be shaded. So, let us put $x = 0$ and $y = 0$ in the equation.
$0 < 0 + 4$
$0 < 4$, which is true.
Hence, the points $(0,0)$ will be included in the shaded region, so the left side of the boundary line will be shaded for this example. As we are only given the “<” sign in the equation, the line itself will not be included and will be termed an open semi-plan.
Practice Questions:
1. Draw the graph for the equation y $\leq$ x – 6. Also, shade the open semi-half of the plane.
2. Draw the graph for the equation y $\geq$ x + 1. Also, shade the open semi-half of the plane.
Answer Keys:
1)
we can plot the graph of the given equation as:
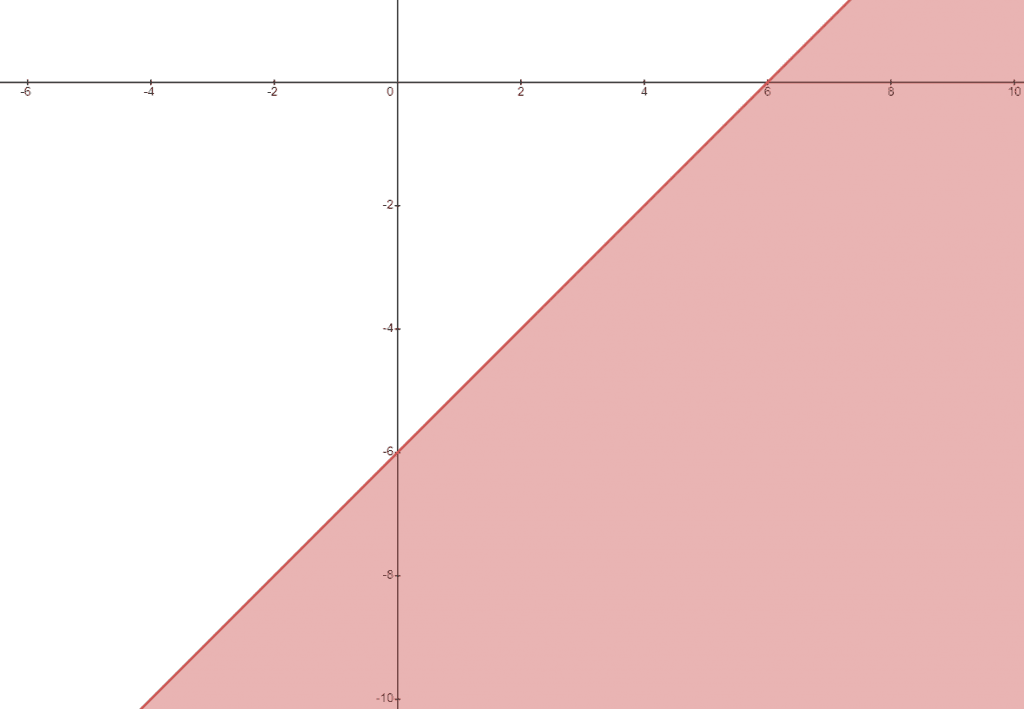
Now to determine which side of the line should be shaded, let us use the (0,0) method. Putting x = 0 and y = 0 in the given equation and see whether it satisfies the equation or not.
y $\leq$ x – 6
0 $\leq$ 0 – 6
0 $\leq$ – 6, which is not true hence we will not include the point (0,0) in the shaded region.
2)
We can plot the graph as follows:
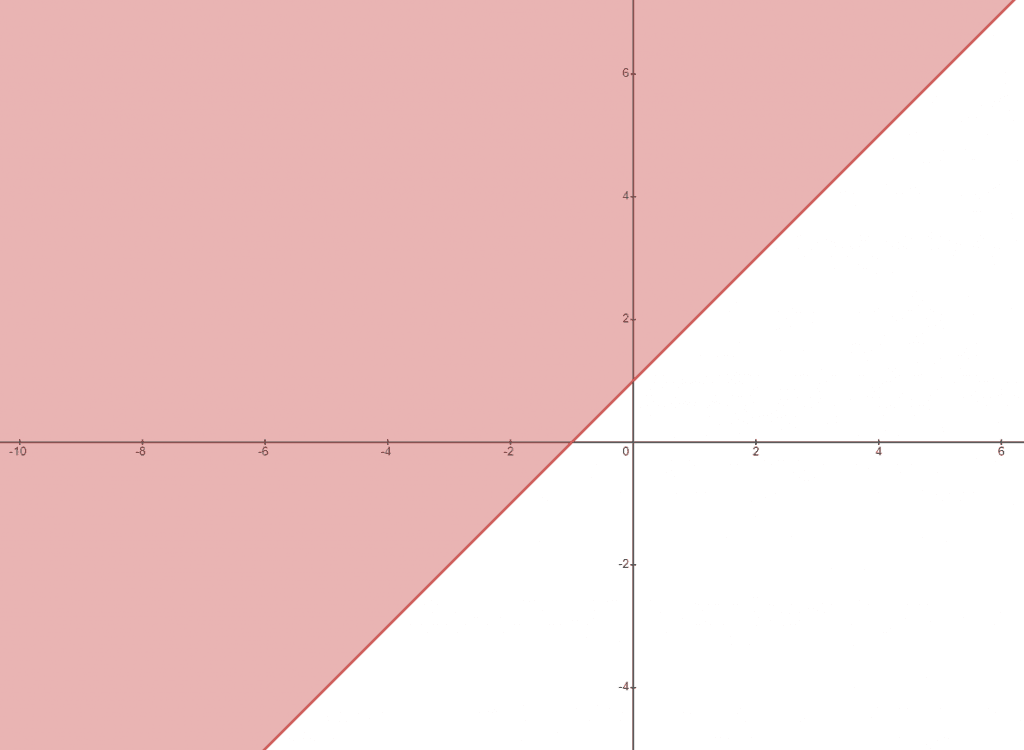
Now to determine which side of the line should be shaded, let us use the (0,0) method. Putting x = 0 and y = 0 in the given equation and see whether it satisfies the equation or not.
y $\geq$ x + 1
0 $\geq$ 0 + 1
0 $\geq$ 1, which is not true hence we will not include the point (0,0) in the shaded region.
