Hexagon – Definition, Geometry, Applications, and Examples

Definition

A hexagon is a geometric figure, a polygon, that has six sides and six vertices. The term originates from the Greek words “hex,” meaning six, and “gonia,” meaning angles. The nature of a hexagon can vary depending on its attributes. If all of its sides and angles are equal, it’s known as a regular hexagon, exhibiting perfect symmetry. Below is the generic diagram for a Hexagon having 6 sides.

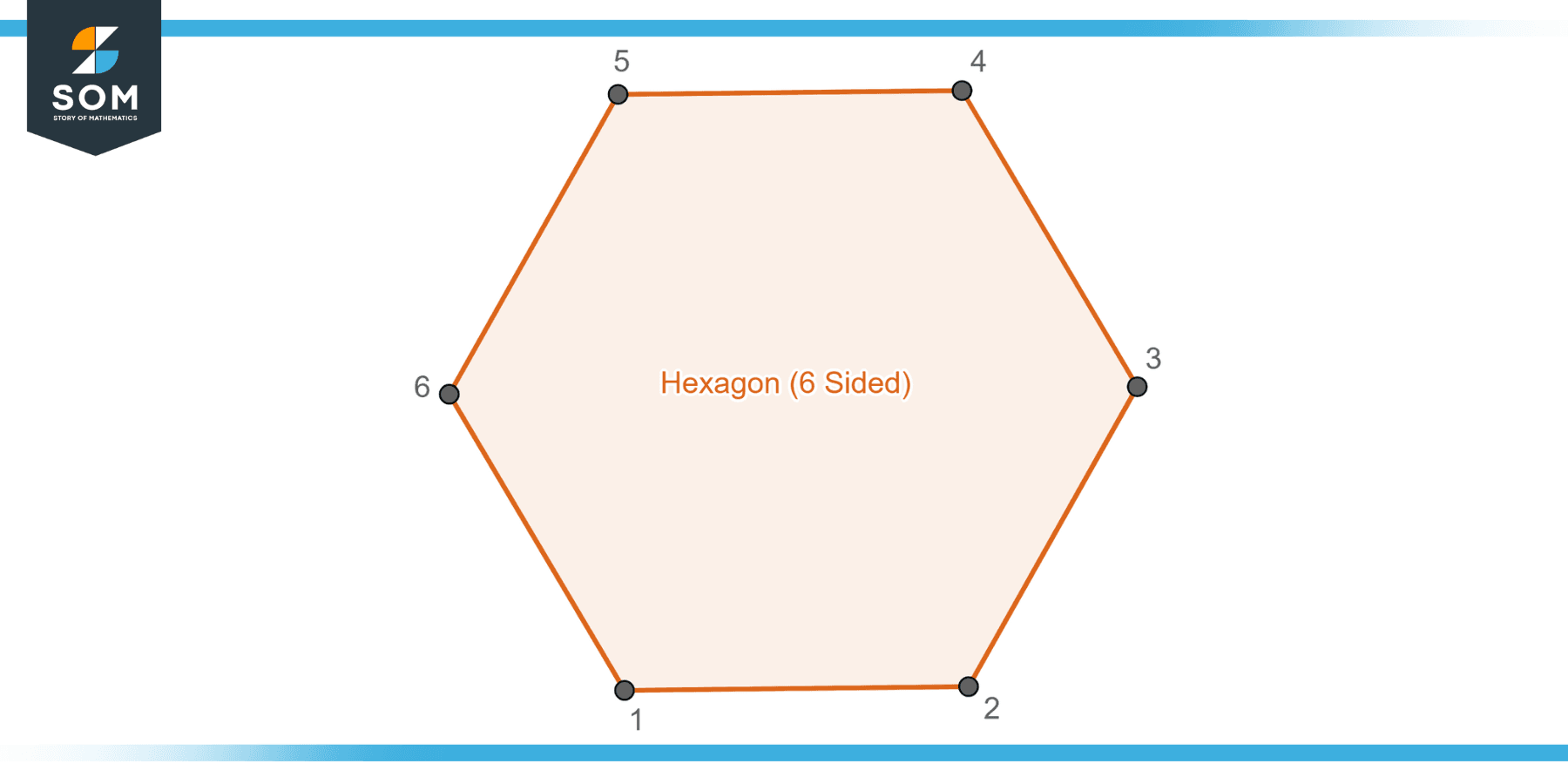
Figure-1: Generic hexagon.

Regular hexagons have interior angles of 120 degrees each, exterior angles of 60 degrees each, and the ability to tile a plane without any gaps, also known as tessellation. Conversely, an irregular hexagon has sides and angles that do not necessarily share the same measurements, resulting in a lack of symmetry. Hexagons are prevalent in various aspects of life, from natural phenomena to human-made designs and systems, due to their unique geometric properties.

Historical Significance

Hexagons have a long and rich history in both natural phenomena and human-made structures and symbols, underpinning their historical significance in various cultures and scientific disciplines.

Honeycombs

The hexagonal shape is commonly found in nature, especially in honeycombs built by bees. The honeycomb’s hexagonal structure allows for maximum efficiency in storing honey and maintaining structural stability. The use of hexagons in honeycombs has inspired architects and engineers to incorporate similar principles in their designs.

Crystallography

Hexagonal structures are prevalent in crystallography. Many minerals and crystals, such as quartz and snowflakes, exhibit hexagonal symmetry in their atomic arrangement. The study of crystallography has been instrumental in understanding the nature of matter and has contributed significantly to fields like materials science and chemistry.

NASA’s Hexagon Experiment

In recent history, hexagons gained attention through NASA’s study of Saturn’s north polar storm system, known as the “hexagon.” The Cassini spacecraft, launched in 1997, captured images and data that revealed a persistent hexagonal cloud pattern at Saturn’s north pole. This discovery has fascinated scientists and sparked an interest in understanding atmospheric dynamics and the potential formation of hexagonal patterns in natural systems.

Ancient Architecture

The use of hexagons in human structures can be traced back to ancient architecture. The most famous ancient example is perhaps the Roman Pantheon, a former Roman temple with a hexagonal pattern embedded in the architecture of the massive dome. This pattern was likely chosen for both aesthetic and structural reasons, as the tessellation of hexagons could evenly distribute the weight of the dome.

Art and Design

In art and design, hexagonal patterns have been utilized across different cultures and historical periods. For example, the Islamic geometric pattern often includes hexagonal tessellations for their intricate design and symbolism. Additionally, the Chinese cultural significance of the number six, often associated with smoothness and success, makes hexagonal patterns a popular motif in various artifacts and traditional designs.

Scared Geometry 

Hexagons also play a significant role in sacred geometry, a form of symbolism and design found in spiritual and religious contexts. The Star of David, a hexagram, is one of the most recognizable symbols of Judaism. In Christianity, the “Seal of Solomon,” another hexagonal pattern, has historical significance. The hexagon represents harmony and balance in some interpretations of sacred geometry.

Scientific Significance

From a scientific perspective, the historical significance of hexagons is quite astounding. In the natural world, hexagons are evident in the honeycomb structures made by bees. This shape is used because it is the most resource-efficient: With the least amount of wax, it enables the bees to store the most honey possible. The Giant’s Causeway, a natural rock formation in Northern Ireland, also features predominantly hexagonal columns. The cooling and cracking of hot volcanic basalt form these.

On a larger scale, hexagons appear in atmospheric patterns on planets in our solar system. The most famous of these is the persistent hexagonal cloud pattern at Saturn’s North Pole, discovered by the Voyager missions and further investigated by the Cassini mission.

Hexagon’s Geometry

A hexagon, from a geometric perspective, is a six-sided polygon with six angles. The properties of a hexagon can differ considerably depending on whether it is a regular or an irregular hexagon.

Let’s start with a regular hexagon, which is a special type of hexagon where all sides and angles are congruent.

Each internal angle is 120 degrees. This is because the sum of the internal angles of any polygon is (n-2) × 180 degrees, where n is the number of sides. For a hexagon, this gives us (6-2) × 180 = 720 degrees. Dividing this by 6 (since a regular hexagon has 6 equal angles), each internal angle measures 120 degrees.

Each external angle of a regular hexagon is 60 degrees. This comes from the fact that the sum of the internal angle and the adjacent external angle on a straight line is 180 degrees. So, 180 – 120 (the internal angle) = 60 degrees.

The perimeter of a regular hexagon is simply six times the length of one side, given that all sides are of equal length.

The formula can be used to get the area (A) of a regular hexagon.  $A = \frac{3 \times \sqrt{3}}{2} \times s^2  $, where s is the length of a side. This equation is the result of the division of a regular hexagon into six equilateral triangles.

An irregular hexagon, on the other hand, has sides and angles that are not necessarily congruent. Because of the variability of an irregular hexagon’s dimensions, there are no simple formulas to calculate the area or perimeter. Typically, to find these values, you’d divide the hexagon into triangles or other shapes, find the areas of these, and then sum them.

Hexagon Types

Hexagons can be categorized into different types based on their properties and characteristics. Here are the main types of hexagons.

Regular Hexagon

A regular hexagon is a hexagon where all six sides and all six angles are equal. It has rotational symmetry of order six, meaning that it can be rotated by multiples of 60 degrees and still maintain the same shape. Regular hexagons are highly symmetrical and have consistent side lengths and interior angles. Below is the diagram for an irregular Hexagon. 

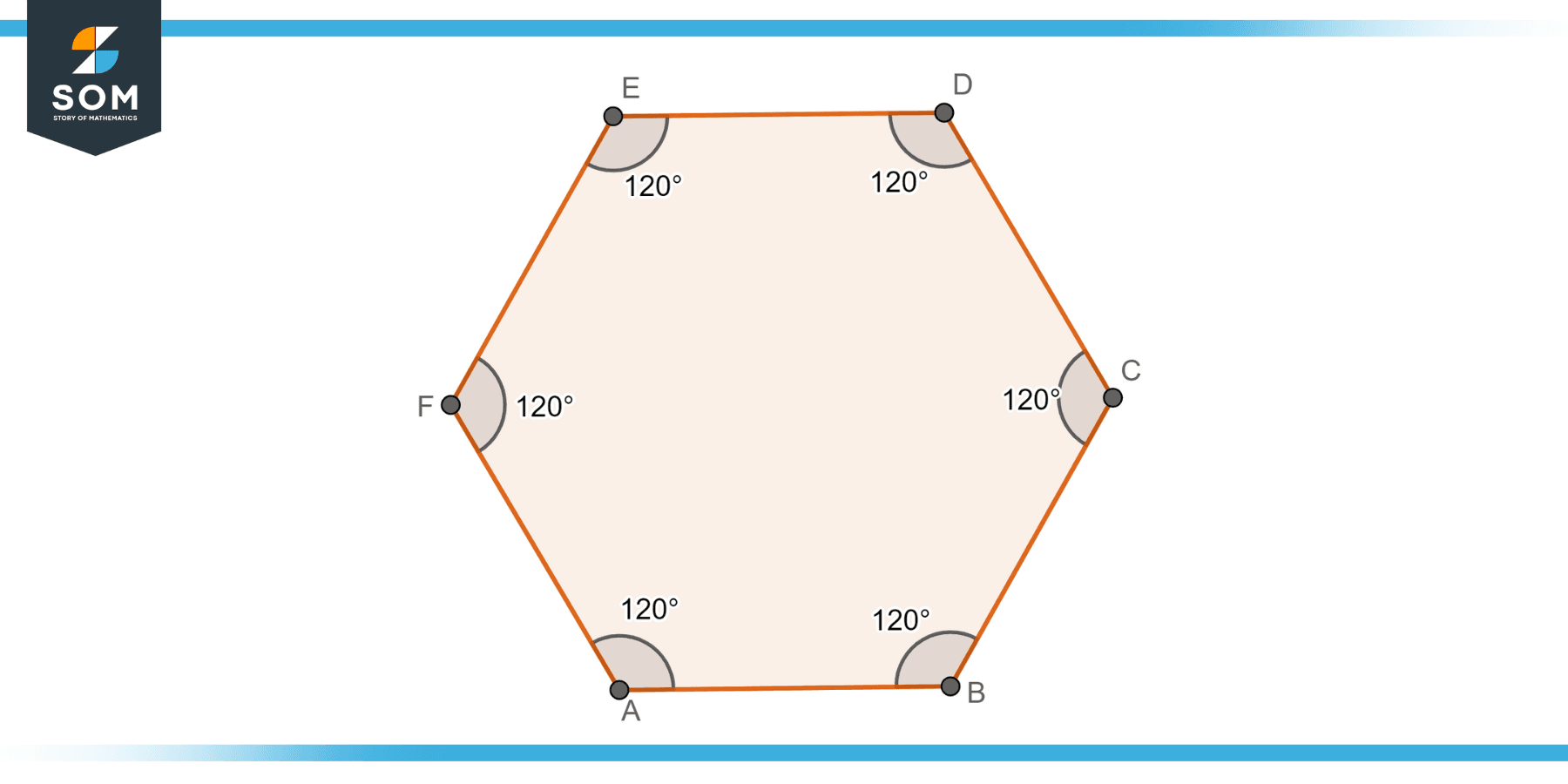
Figure-2: Irregular hexagon.

Irregular Hexagon

An irregular hexagon is a hexagon that does not have equal side lengths or equal interior angles. Its sides and angles can have different measures, and it lacks the rotational symmetry found in regular hexagons. Irregular hexagons can have a variety of shapes and sizes. Below we present the geometric shape of an irregular Hexagon. 

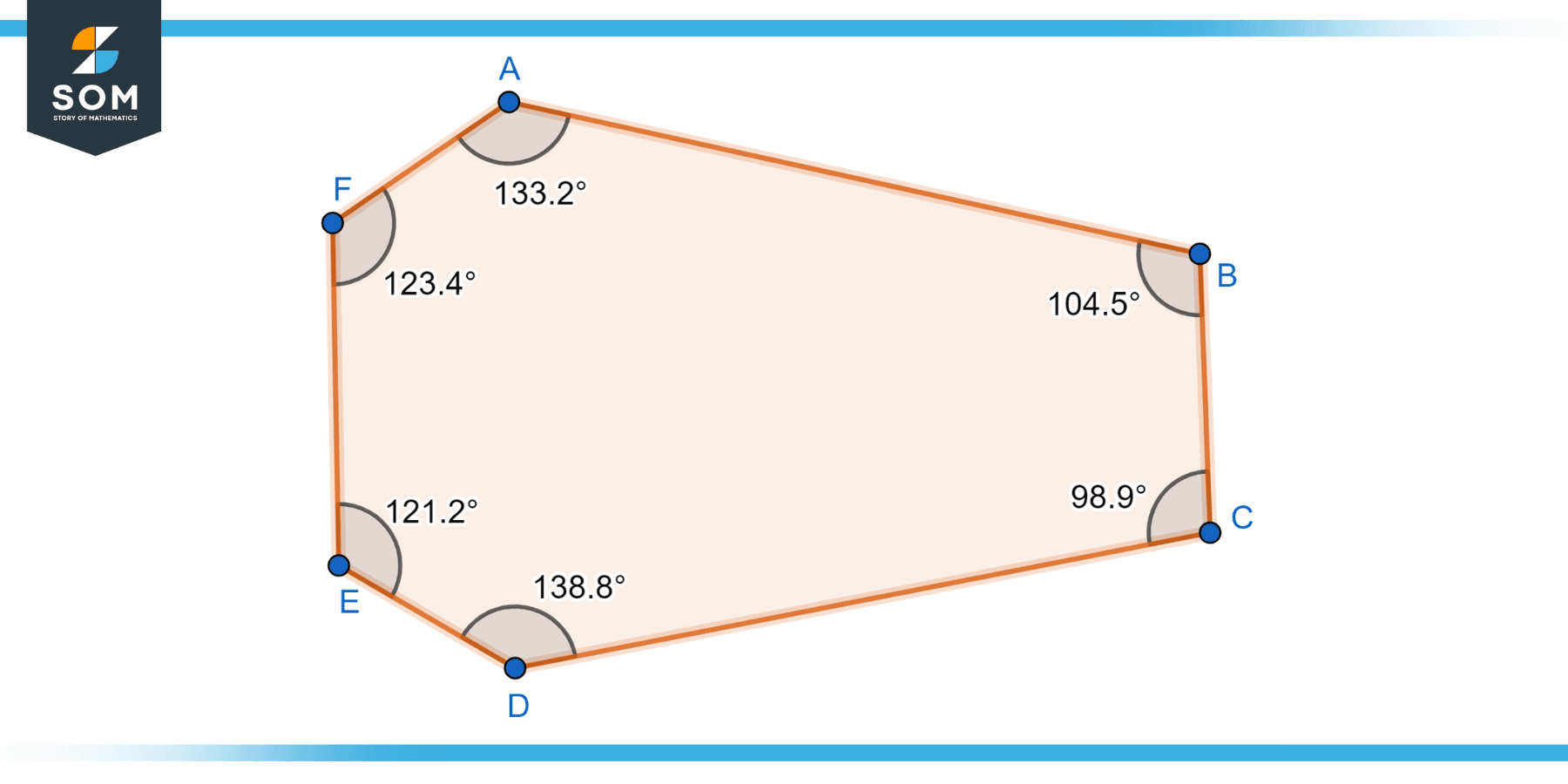
Figure-3: Irregular hexagon.

Convex Hexagon

A convex hexagon is a hexagon in which no interior angle is greater than 180 degrees. All the sides of a convex hexagon point outwards, giving it a “bowed out” appearance. Convex hexagons are often the focus of geometric studies due to their simplicity and well-defined properties. Below we present the geometric diagram of an irregular convex Hexagon.

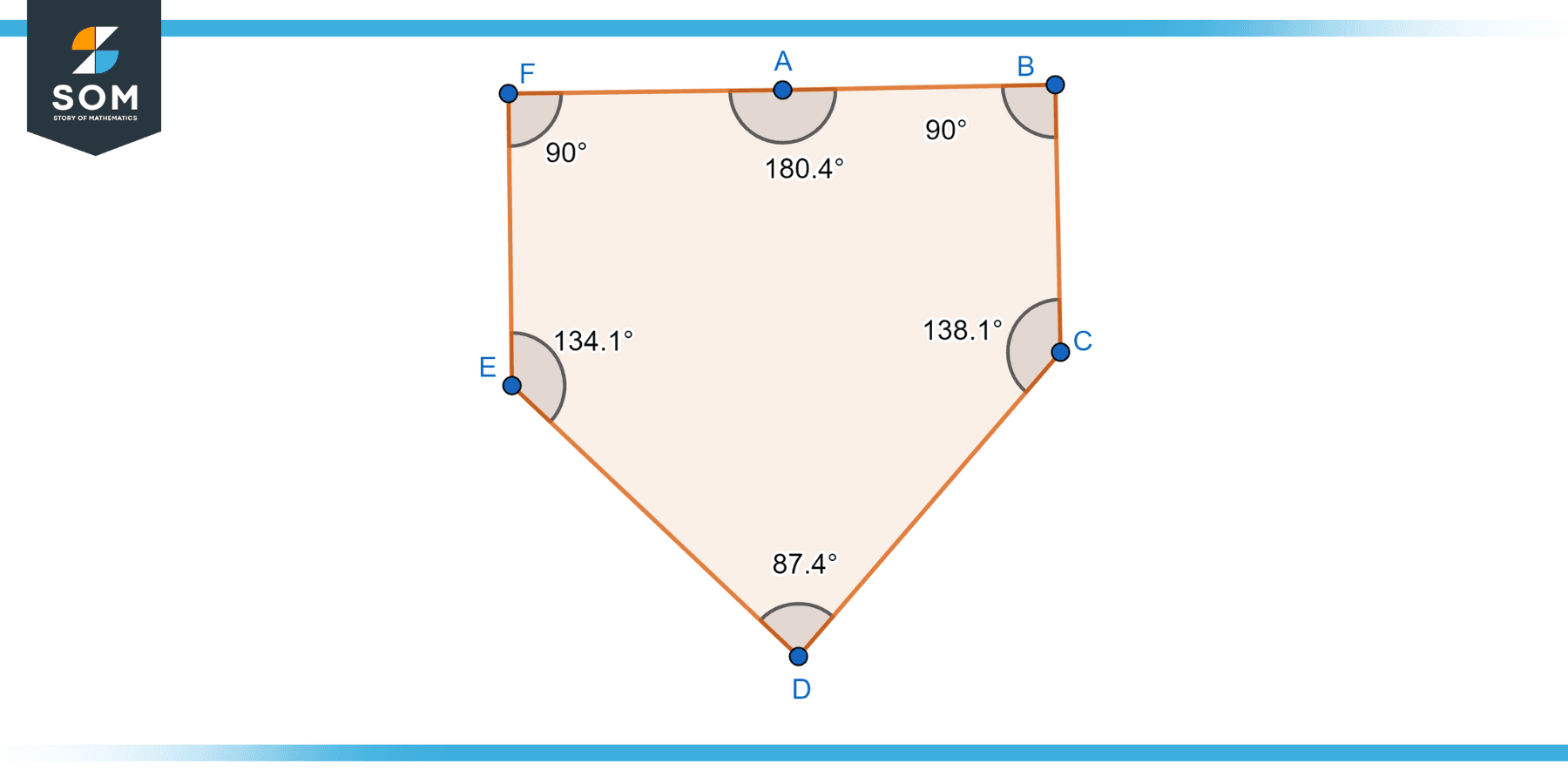
Figure-4: Irregular convex hexagon.

Concave Hexagon

A concave hexagon is a hexagon whose inner angles are larger than 180 degrees at least on one occasion. It has at least one “caved-in” or indented side. Concave hexagons can have irregular shapes and exhibit more complex geometrical properties compared to convex hexagons. Below is the diagram of an irregular concave Hexagon.

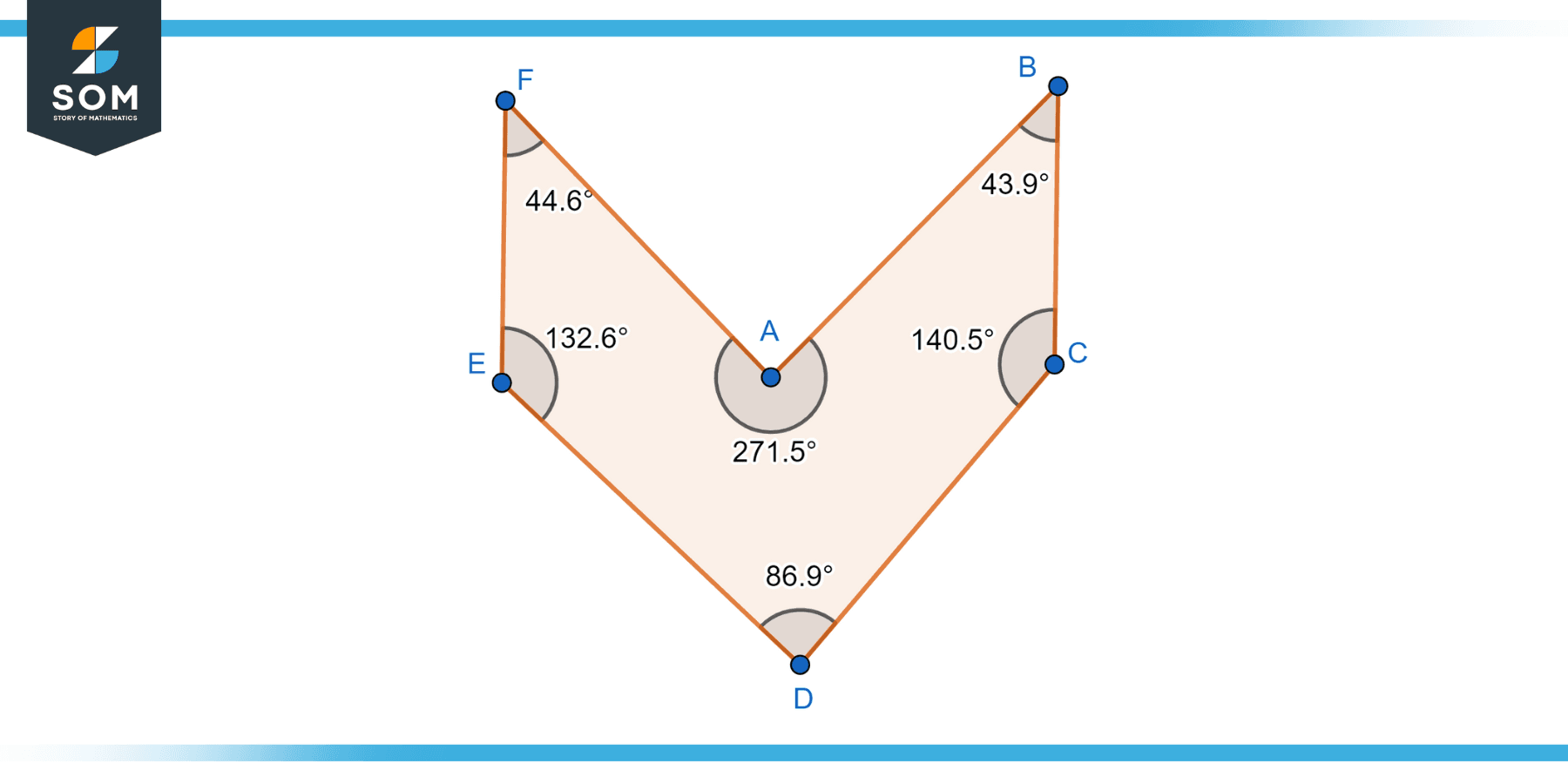
Figure-5: Irregular concave hexagon.

Relevant Formulae

Below are the relevant formulas related to a hexagon, specifically a regular hexagon, given that an irregular hexagon does not have simple, universal formulas due to its variable dimensions. For these formulas, we assume a regular hexagon with side lengths ‘s.’

Perimeter

The perimeter of a hexagon is simply the sum of the lengths of its sides. For a regular hexagon, all sides are of equal length. So, the perimeter (P) is:

P = 6 × s

Interior Angle

The total measure of the interior angles of any polygon is given by the formula (n-2) × 180, where ‘n’ is the number of sides. For a hexagon, this gives us (6-2) × 180 = 720 degrees.

Each individual interior angle of a regular hexagon (since a regular hexagon’s angles are all equal) is this total divided by the number of sides (6), which gives us 120 degrees.

Exterior Angle

For any regular polygon, the measure of each exterior angle is 360/n degrees. In the case of a regular hexagon, this is 360/6 = 60 degrees.

Area

The area of a regular hexagon can be found by dividing it into six equilateral triangles. The area formula is:

$$A = \frac{3 \times \sqrt{3}}{2} \times s^2 $$

This formula is derived from calculating the area of each equilateral triangle and then multiplying by 6.

Diagonals

A hexagon is a six-sided polygon. Every vertex (or corner) of the hexagon is connected to every other vertex by a line segment. Some of these are sides of the hexagon, and the rest are diagonals. A diagonal is a line segment that joins two polygonal vertices that are not contiguous to one another. For a hexagon, each vertex is connected to three other vertices by a diagonal.

To find the total number of diagonals, we use the formula:

n × (n-3)/2,

where n is the number of vertices (or corners) of the polygon.

Apothem and Radius

The apothem of a regular hexagon (a line that connects the hexagon’s centre to any of its side’s midpoints) and the radius (a line from the center to any vertex) are particularly useful in certain calculations.

For a regular hexagon with side length ‘s’ Apothem (a) is given by:

$$a = \frac{s \times \sqrt{3}}{2} $$

Radius (r) = s

Using the Apothem or Radius for Area

Alternatively, the area of a regular hexagon can be found using the apothem (a) or the radius (r) with these formulas:

Using the apothem: A = 1/2 × a × P,

where P is the perimeter of the hexagon.

Using the radius, the area could be calculated as:

$$\frac{3}{2} \times r^2 \times \sqrt{3}$$

Applications

Hexagon is a powerful geometric shape with six sides and six angles. It has various applications across different fields due to its unique properties and symmetry. Here, we’ll discuss some of the key applications of hexagons in various domains.

Mathematics and Geometry

Hexagons have long been of interest in mathematics and geometry due to their regularity and tessellating properties. Hexagonal tessellations are highly efficient in covering a plane without any gaps or overlaps. This property makes them useful in fields such as crystallography, where hexagonal lattices are used to represent atomic structures. Hexagons are also integral to the study of hexagonal geometry, which includes topics like hexagonal numbers, hexagonal tilings, and hexagonal grids.

Architecture and Construction

Hexagons are aesthetically pleasing shapes that find applications in architectural design. The regular hexagonal shape can be used in the layout of buildings, city planning, and urban design. Honeycomb structures, which consist of hexagonal cells, are known for their strength and efficiency. They are used in various construction applications, such as lightweight composite materials, aerospace components, and structural supports.

Manufacturing and Engineering

Hexagons play a crucial role in the manufacturing and engineering industries. Hexagonal wrenches and socket sets are widely used for tightening and loosening bolts and screws due to the multiple contact points provided by the six-sided shape. Hex bolts and nuts, known as hex cap screws, are extensively used in machinery, automotive, and construction sectors. The use of hexagons in these fasteners ensures a secure grip and minimizes the risk of stripping or rounding off the corners.

Computer Science and Data Representation

Hexadecimal, often referred to as “hex,” is a number system that uses a base of 16. It is frequently employed in digital systems and computer science. Hexadecimal representation allows concise and efficient representation of binary data, particularly in computer memory and programming. Hex codes are used to represent colors in web design, where each color is specified by a six-digit hexadecimal number. Hex grids are also used in computer graphics and game development for representing maps and game worlds.

Nature and Biology

Hexagons are found abundantly in nature and biology. For example, honeybees construct their hives using hexagonal cells, as it maximizes the use of space while minimizing the amount of wax needed. The efficiency of hexagonal packing can also be observed in the arrangement of cells in plant structures, such as the pattern found in the skin of a pineapple. Additionally, some compounds and molecules, such as benzene, have hexagonal structures.

Communication and Networking

Hexagons are employed in the field of wireless communication and networking. Hexagonal cell grids are commonly used in cellular network planning and optimization. The hexagonal layout provides better coverage and capacity compared to other geometric shapes, such as squares or circles. This design allows for a more efficient distribution of base stations and minimizes interference between neighboring cells.

In essence, hexagons have a wide range of applications across various fields thanks to their unique geometric properties. From natural formations to human-made structures and systems, their influence and utility are pervasive.

Exercise

Example 1

Find the sum of the interior angles of a hexagon.

Solution

The formula for the sum of the interior angles of a polygon is (n-2) × 180°, where n is the number of sides. In the case of a hexagon, n = 6.

Substituting the value into the formula: (6-2) × 180° = 720°

So, the sum of the interior angles of a hexagon is 720°.

Example 2

A hexagon is regular, which means all of its sides and angles are equal. If one angle measures 120 degrees, is it a regular hexagon?

Solution

In a regular hexagon, each interior angle can be calculated by the formula (n-2) × 180° / n, where n is the number of sides. For a hexagon, n = 6.

Substituting n = 6 in the formula gives us: (6-2) × 180° / 6 = 120°

So, yes, it is a regular hexagon.

Example 3

What is the measure of each interior angle of a regular hexagon?

Solution

Use the same formula as above: (n-2) × 180° / n. For a hexagon, n = 6.

Substitute n = 6 in the formula: (6-2) × 180° / 6 = 120°

So, each interior angle of regular hexagon measures 120°.

Example 4

What is the measure of each exterior angle of a regular hexagon?

Solution

The exterior angle of a regular polygon can be found using the formula 360° / n.

For a hexagon, n = 6. Substitute n = 6 into the formula: 360° / 6 = 60°

So, each exterior angle of the regular hexagon measures 60°.

Example 5

For a regular hexagon given in Figure-6, what is its perimeter?

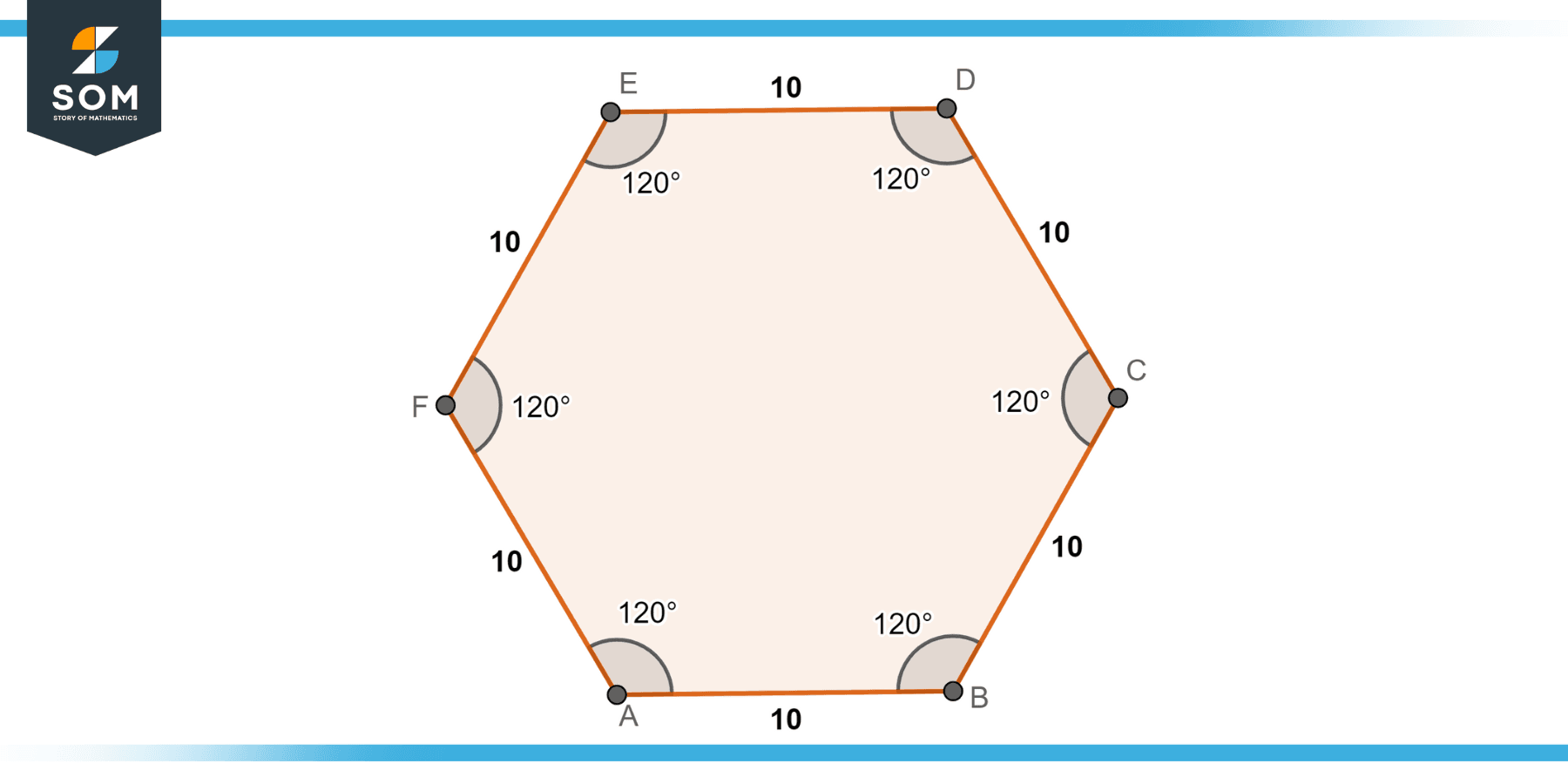
Figure-6.

Solution

The perimeter of a regular polygon is calculated by multiplying the length of one side by the number of sides.

 For a regular hexagon with a side length of 10 units, the perimeter is 6 × 10 = 60 units.

So, the perimeter of the hexagon is 60 units.

Example 6

The area of a regular hexagon is 259.8076 square units. What is the length of each side?

Solution

The area of a regular hexagon can be found using the formula $A = (\frac{3 \times \sqrt{3}}{2} \times s^2 ) $, where s is the length of a side.

Rearrange the formula to find s: we get

$$s = sqrt{( \frac{A}{\frac{3 \times \sqrt{3}}{2}} )}$$

Substitute A = 259.8076 into the formula:

$$s = sqrt{( \frac{259.8076}{\frac{3 \times \sqrt{3}}{2}} )}$$

s ≈ 10 units.

So, each side of the hexagon is approximately 10 units long.

Example 7

A regular hexagon has a side length of 8 units. What is its area?

Solution

Use the area formula for a regular hexagon, $A = \frac{3 \times \sqrt{3}}{2} \times s^2  $.

Substitute s = 8 into the formula we get

$$A = \frac{3 \times \sqrt{3}}{2} \times 8^2  $$

A ≈ 166.2766 square units.

So, the area of the hexagon is approximately 166.2766 square units.

Example 8

A hexagon has 6 vertices. How many diagonals does it have?

Solution

The number of diagonals in a Using the formula n × (n-3)/2, where n is the number of sides, polygons can be computed.

For a hexagon, n = 6. Substitute n = 6 into the formula: 6 × (6-3)/2 = 9.

So, a hexagon has 9 diagonals.

All images were created with GeoGebra.