
The interesting and varied realm of three-dimensional geometry is full of mind-boggling and imaginative shapes. Among these is the hyperboloid, a captivating surface that finds its place in mathematics and the real world. This geometric marvel belongs to the family of quadric surfaces, characterized by equations of the second degree in three variables. But the hyperboloid has a twist unlike its quadric cousins – the ellipsoids, paraboloids, and cones. Distinguished by its unique ‘saddle’ shape, it’s a figure that challenges our understanding of geometry and has practical applications in architecture, engineering, and physics.
This page explores the hyperboloid’s intricate mathematical features, formulas, and applications and its astonishing role in our environment.
Definition
A hyperboloid is a three-dimensional geometric shape that falls into quadric surfaces. Quadric surfaces are three-dimensional shapes that a second-degree equation can describe in three variables. Hyperboloids are typically defined by one of two standard equations, which result in two primary types of hyperboloids, hyperboloid of one sheet and hyperboloid of two sheets. Below we present a generic structure of a hyperboloid.
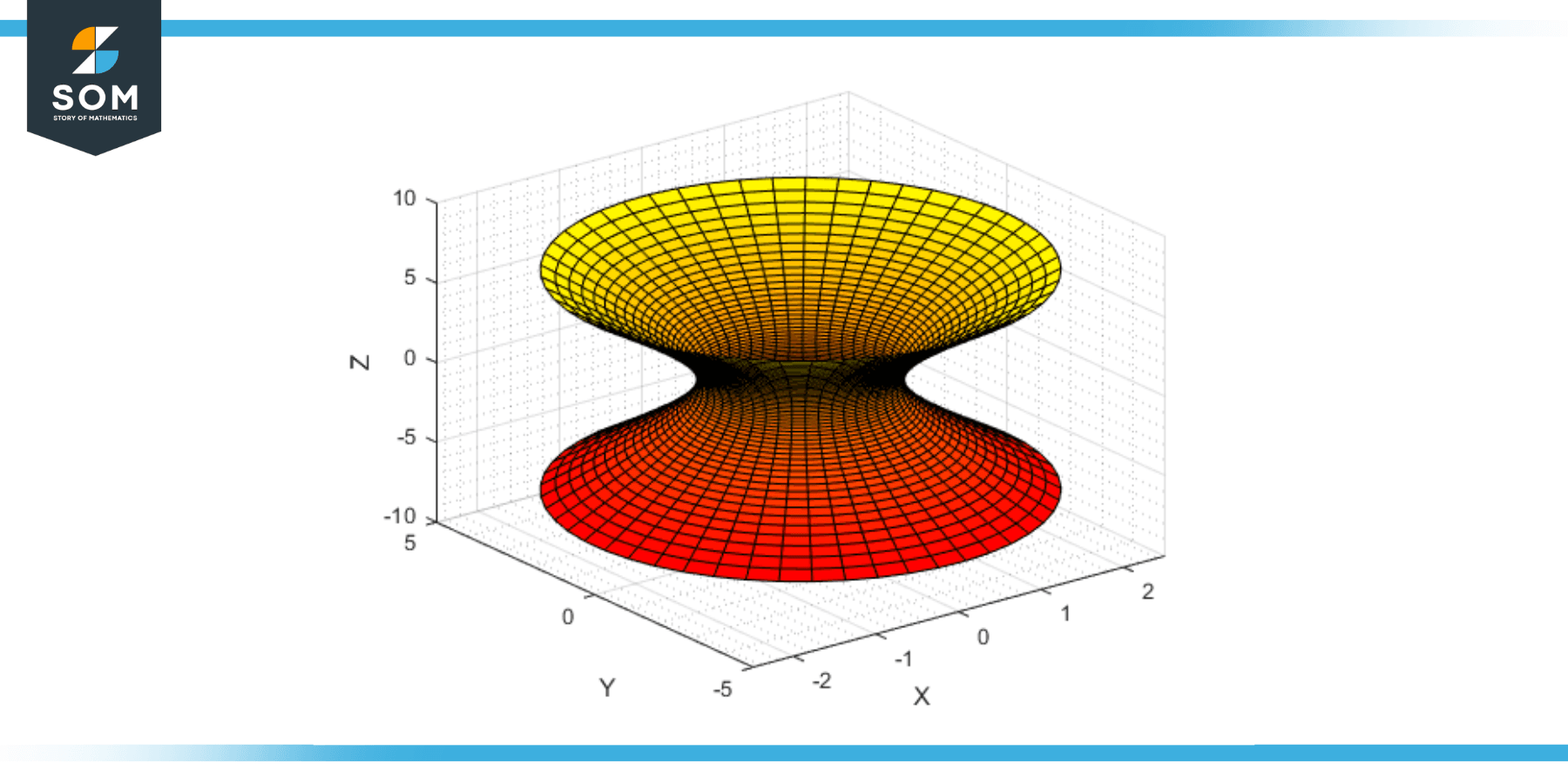
Figure-1: Generic hyperboloid.
The unique structure of hyperboloids results in some intriguing properties. For instance, they possess a characteristic known as negative Gaussian curvature. This feature means that, like a saddle, the surface curves upwards in one direction and downwards in the other around any point on the surface. Because of their unique geometric properties and structural robustness, hyperboloids find applications in various fields, including architecture, engineering, and physics.
Historical Significance
The historical background of the hyperboloid encompasses several centuries of mathematical exploration and geometric study. The development of this captivating shape can be traced back to significant contributions from mathematicians, engineers, and architects throughout history.
The Greek mathematician Euclid is credited with creating the field of hyperbolic geometry by laying the groundwork for studying geometrical features and shapes.
Mathematicians didn’t start focusing on the hyperboloid as a separate geometric shape until the 19th century.
Nikolai Lobachevsky, a mathematician from Russia, made important contributions to non-Euclidean geometry, especially hyperbolic geometry.
His work during the 19th century opened the door for a fuller comprehension of the characteristics of the hyperboloid and its connection to hyperbolic space.
The study of hyperboloids gained popularity in the late 19th and early 20th centuries, especially in architecture. Influential architects such as Vladimir Shukhov and Antoni Gaudí utilized hyperboloid structures in their designs, pushing the boundaries of architectural innovation.
The Shukhov Tower in Russia, created by Vladimir Shukhov in 1920, is one of the most recognizable examples of hyperboloid architecture. This lattice hyperboloid structure was aesthetically striking and demonstrated the strength and stability of hyperboloid designs.
The 20th century witnessed further exploration and refinement of hyperboloid geometry, with advancements in mathematical modeling, computer-aided design, and fabrication techniques. These developments allowed for the creation of more complex and intricate hyperboloid structures.
Geometry
The hyperboloid is a captivating geometric shape, distinguished by its unique ‘saddle’ shape. The two primary varieties of hyperboloids, the hyperboloid of one sheet and the hyperboloid of two sheets, each have a number of important geometric characteristics that we will now examine:
One-Sheet Hyperbolic Projection
This hyperboloid resembles a stretched-out hourglass or a power plant cooling tower. It is an unbounded surface extending infinitely in positive and negative z-directions. It has a point of symmetry at the origin, called the vertex. Its cross sections are hyperboles along the vertical axis (z-axis) and ellipses along the horizontal axes (x and y). These sections are symmetrical due to the rotational symmetry of the surface. The hyperboloid of one sheet has two separate branches of hyperbolas running in different directions along the z-axis, giving it a distinctive ‘double cone’ appearance.
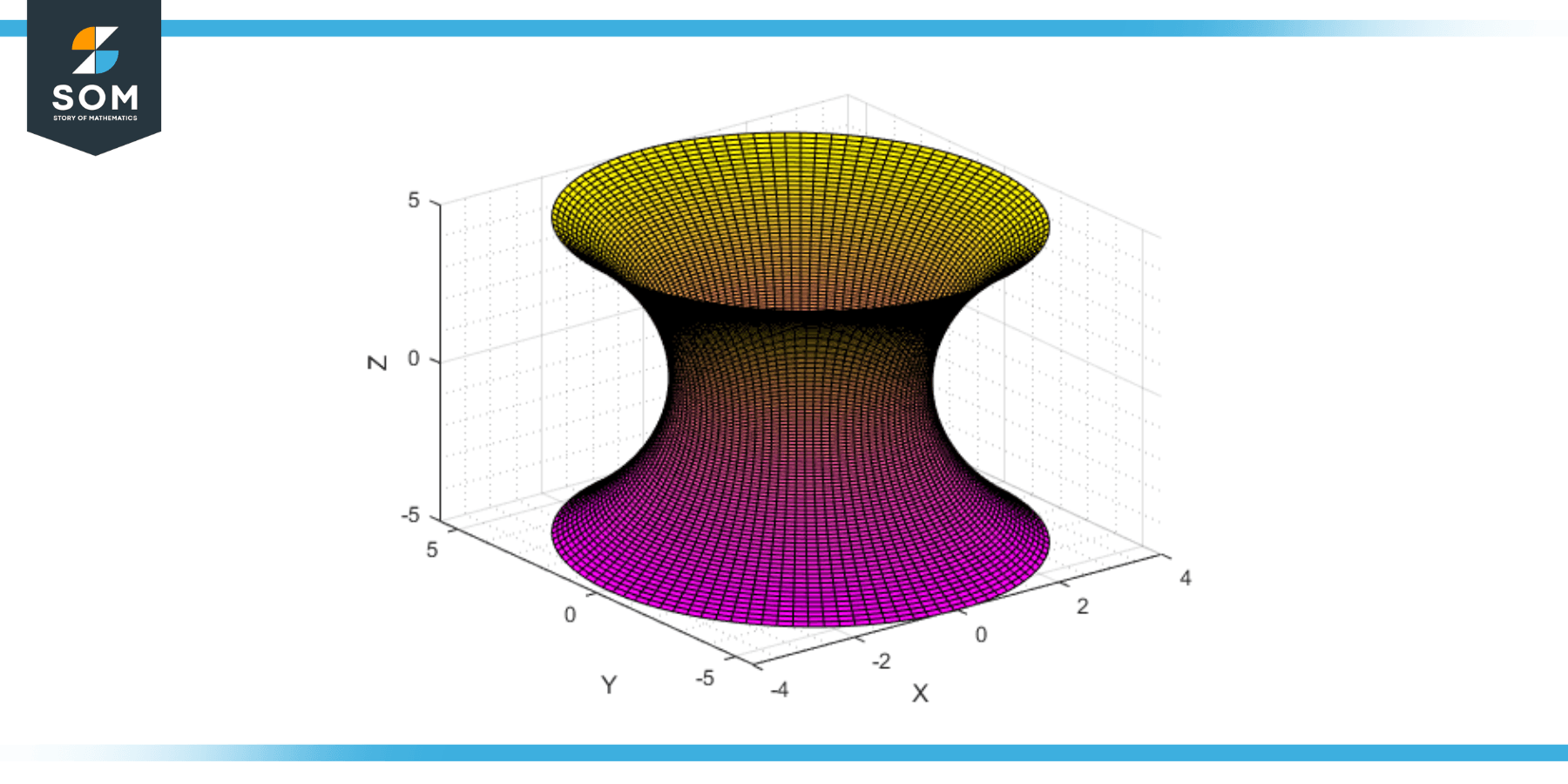
Figure-2: One-sheet hyperboloid.
Hyperboloid of Two Sheets
This type of hyperboloid appears as two separate, unconnected parts, which look like two paraboloids opening in opposite directions.
It is also an unbounded surface that extends infinitely in both the positive and negative z-directions but with a gap in between. This type of hyperboloid has no points of intersection. Instead, it is characterized by a gap or void region along the z-axis, separating the two hyperboloid sheets. Contrary to one sheet’s hyperboloid, the two sheets’ hyperboloid lacks rotational symmetry. Its cross sections are also hyperboles along the z-axis and ellipse along the x and y-axis. The hyperbolas of the cross sections are oriented in different directions on each sheet.
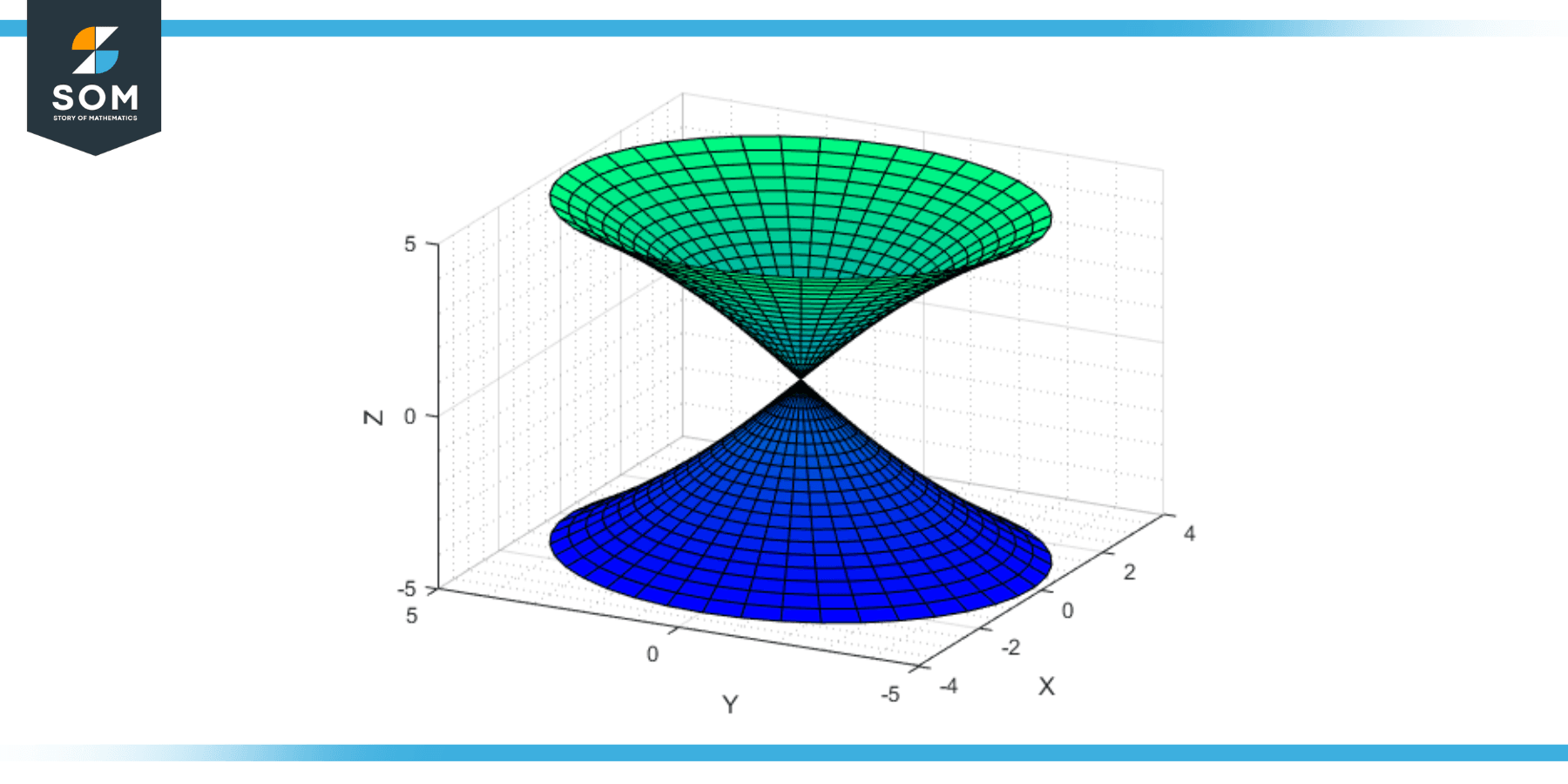
Figure-3: Two-sheet hyperboloid.
Ralevent Formulas
The hyperboloid is a fascinating geometric shape, and understanding its properties requires familiarity with the formulas that define it. There are two main types of hyperboloids, each described by its own formula:
Hyperboloid of One Sheet
The standard equation for a hyperboloid of one sheet is x²/a² + y²/b² – z²/c² = 1. This equation describes a single, continuous surface that opens up in two opposite directions, resembling a double cone or a cooling tower at a power plant. Here, a, b, and c are real positive constants that determine the shape and size of the hyperboloid.
Hyperboloid of Two Sheets
The standard equation for a hyperboloid of two sheets is x²/a² + y²/b² – z²/c² = -1. This equation describes two separate, unconnected surfaces that resemble two paraboloids opening away from each other. Like in the first equation, a, b, and c are real positive constants that determine the shape and size of the hyperboloid.
Depending on the values of a, b, and c, these formulas can describe hyperboloids in various shapes and sizes. For example, if a = b, the cross-section of the hyperboloid in the xy-plane will be a circle, resulting in a circular hyperboloid.
Additionally, hyperboloids exhibit a property known as negative Gaussian curvature, which is calculated by the formula K = -1/(a²b²c²). This property, signifying that the surface curves upwards in one direction and downwards in the other around any point on the surface is one of the most distinctive characteristics of hyperboloids.
Finally, it’s worth noting that the formulas for a hyperboloid’s volume or surface area are quite complex and involve advanced mathematical techniques, such as integral calculus. However, they are typically less frequently used than the basic defining equations for the hyperboloid of one sheet and the hyperboloid of two sheets.
Applications
With its distinctive shape and versatile properties, the hyperboloid finds applications across various fields. From architecture and engineering to physics and design, the hyperboloid offers unique opportunities for practical and aesthetic utilization. Let’s explore some of its key applications:
Architecture and Structural Engineering
The hyperboloid’s graceful form and inherent structural stability make it a favored choice in architectural design. It is commonly employed to construct iconic structures like towers, pavilions, and bridges. The hyperboloid’s curved surfaces distribute loads efficiently and offer high strength-to-weight ratios, creating visually striking and structurally sound buildings.
Cooling Towers
Hyperboloid structures are extensively used in cooling towers of power plants and industrial facilities. The shape facilitates efficient air circulation and heat dissipation. The upward draft created by the hyperboloid’s conical form allows for effectively cooling water or gases, making it an essential component in thermal power plants and industrial processes.
Antenna Systems
The hyperboloid shape is advantageous in designing antenna systems for telecommunications and radar applications. It provides a wide radiation pattern, allowing for improved signal coverage. Hyperboloid reflectors and arrays are used in radio astronomy, satellite communications, and wireless networks to transmit and receive signals effectively over long distances.
Optics and Acoustics
Hyperboloid surfaces are utilized in optics and acoustics to control light and sound propagation. The shape’s reflective properties make it valuable for designing parabolic mirrors, telescopes, and acoustic reflectors. In optical systems, hyperboloid lenses and mirrors are employed to focus or disperse light, while hyperboloid reflectors enhance sound projection and diffusion in concert halls and auditoriums.
Industrial Design and Sculpture
The captivating form of the hyperboloid has inspired its incorporation into industrial design and sculpture. Designers and artists leverage its dynamic curves to create aesthetically pleasing and visually engaging products, furniture, and art installations. The symmetrical and flowing nature of the hyperboloid lends itself to modern and contemporary design aesthetics.
Mathematical Modeling and Research
Hyperboloids serve as essential mathematical models in fields like differential geometry and physics. Mathematicians and researchers use hyperboloids to study curvature, develop geometric proofs, and analyze physical phenomena. Hyperboloid equations and parametric representations provide valuable tools for investigating mathematical concepts and solving complex problems.
Kinetic Architecture
The hyperboloid’s ability to create visually captivating and adaptable structures has led to its application in kinetic architecture. Hyperboloid-shaped elements can be dynamically transformed, allowing buildings and structures to adjust their form and adapt to changing environmental conditions or functional requirements.
Exercise
Example 1
Identifying a hyperboloid
Given the equation, x²/16 + y²/9 – z²/4 = 1, determine if the equation represents a hyperboloid, and if so, which type it is.
Solution
This equation matches the standard form for a hyperboloid of one sheet, x²/a² + y²/b² – z²/c² = 1, where a = 4, b = 3, and c = 2.
Example 2
Identifying a hyperboloid
Given the equation x²/4 + y²/9 – z²/16 = -1, determine if the equation represents a hyperboloid, and if so, which type it is.
Solution
This equation matches the standard form for a hyperboloid of two sheets, x²/a² + y²/b² – z²/c² = -1, where a = 2, b = 3, and c = 4.
All images were created with GeoGebra.
