JUMP TO TOPIC

In geometry, the annulus stands as a captivating and intriguing geometric shape. Defined as the region between two concentric circles, the annulus possesses a unique elegance that makes it visually appealing and mathematically significant. With its distinct properties and applications in various fields, the annulus unveils a world of geometric exploration and practical utility. From calculating areas and circumferences to understanding its relation to circles and sectors, the annulus captivates the minds of mathematicians and enthusiasts alike.
In this article, we embark on a journey of discovery, delving into the intricacies of annuli, exploring their properties, examining their formulas, and unveiling their presence in everyday life. So, let us embark on this geometric adventure and immerse ourselves in the enthralling annuli universe.
Definition
The annulus is a geometric shape that refers to the region between two concentric circles. It is described as the collection of all points in a plane inside and outside the outer circle. The annulus is characterized by its two radii: the outer radius (denoted as R) representing the distance from the center of the annulus to the outer circle, and the inner radius (denoted as r) representing the distance from the center to the inner circle. Below we present the generic diagram of an annulus.
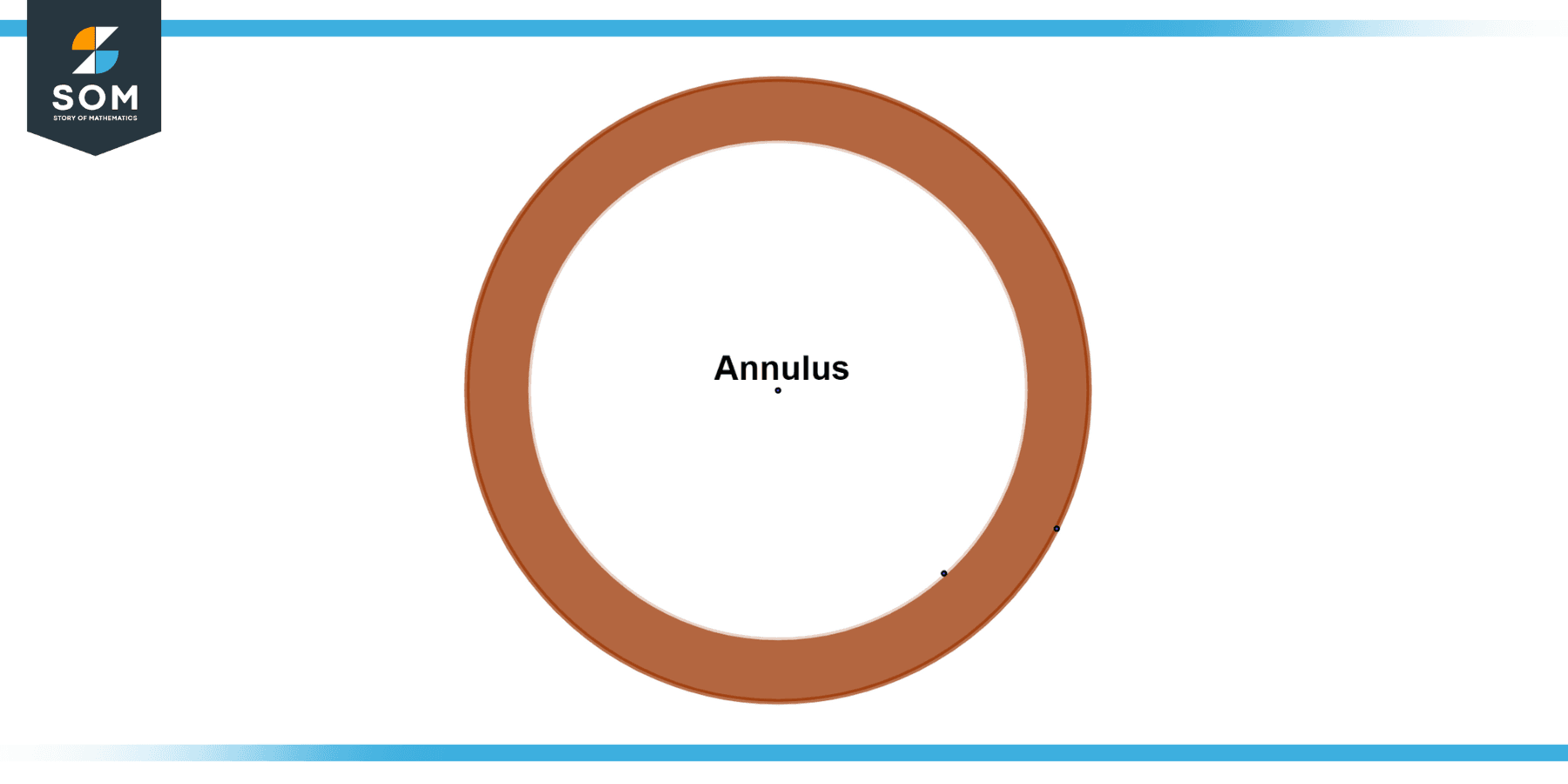
Figur-1: Generic annulus.
The annulus is a two-dimensional shape with a circular shape on the outside and a circular hole on the inside. It can be visualized as a ring or a disk with a removed center. The annulus is commonly encountered in various fields of mathematics, physics, engineering, and design due to its unique properties and applications.
Historical Significance
The historical background of the annulus, a geometric shape, can be traced back to ancient civilizations and the development of geometry as a mathematical discipline. The concept of circles and their properties, which form the basis of the annulus, has been studied and explored by ancient mathematicians such as Euclid, Archimedes, and Apollonius.
The understanding of circles and their properties led to recognizing the annulus as a distinct geometric shape. The term “annulus” itself is derived from the Latin word “annulus,” meaning “ring.” The annulus was recognized as a region between two concentric circles, with the outer circle representing a larger ring and the inner circle representing a smaller ring.
The study of the annulus and its properties has been an essential part of geometry throughout history. Mathematicians have investigated various aspects of the annulus, including its area, circumference, and relationship with other geometric shapes. The properties of the annulus have been applied in diverse fields, such as architecture, engineering, physics, and design.
Today, the annulus continues to be an important geometric shape in various disciplines. Its unique characteristics, such as the ability to create concentric patterns and its use in circular designs, make it valuable in fields like architecture and art. Additionally, the mathematical understanding of the annulus and its properties contributes to the development of more advanced concepts in geometry and other mathematical disciplines.
Overall, the historical background of the annulus showcases its significance in geometry and its ongoing relevance in modern applications. The exploration and study of the annulus by ancient mathematicians have paved the way for its understanding and utilization in various fields, making it an intriguing and valuable geometric shape.
Types
When it comes to annuli, there are a few main types based on their characteristics. Let’s explore them in detail:
Non-Trivial Annulus
A non-trivial annulus is the most common type of annulus. It has an inner and outer circle that is distinct and concentric. The width of a non-trivial annulus is greater than zero. Below we present the generic diagram of a non-trivial annulus.
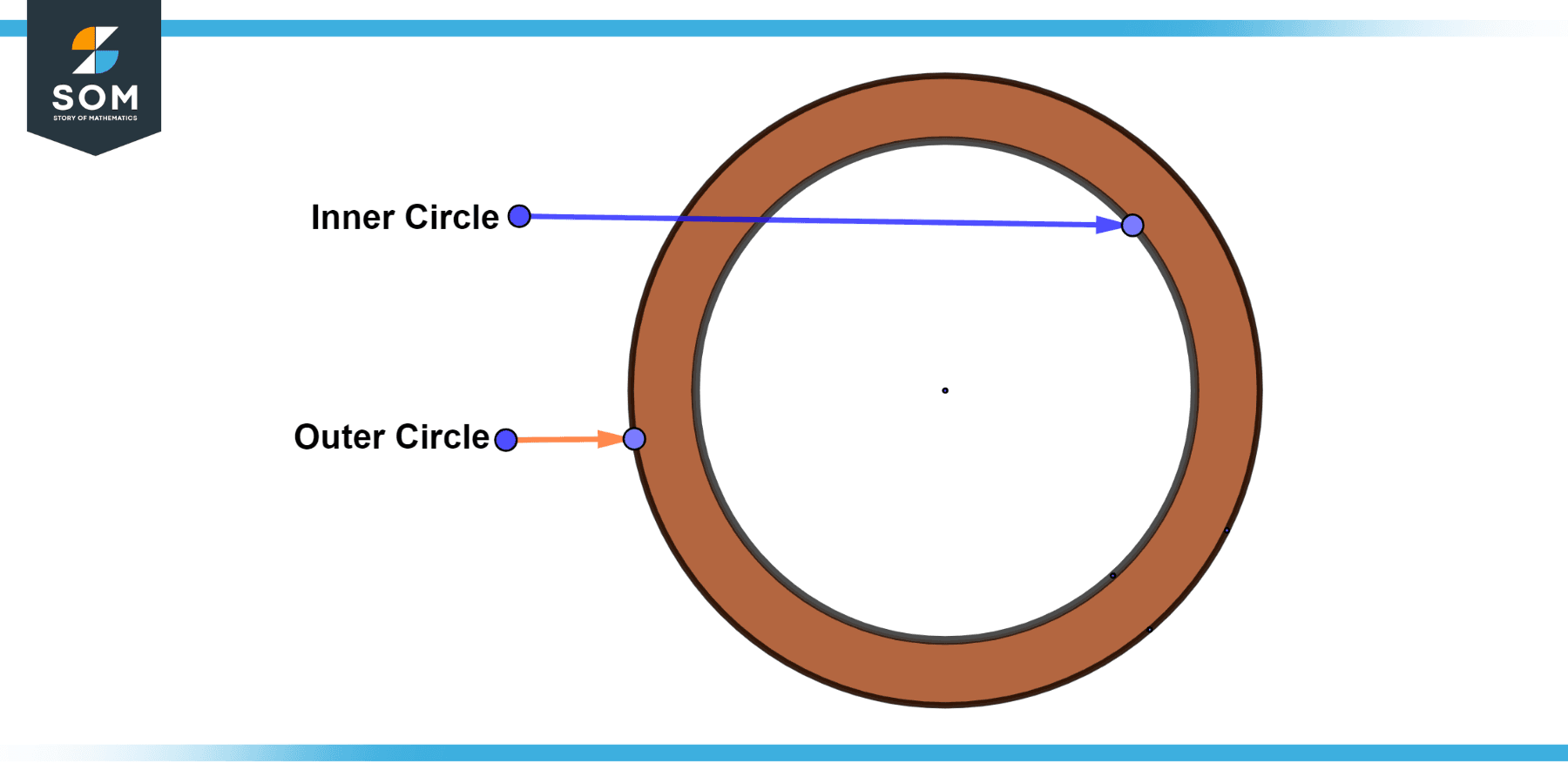
Figure-2: Non-trivial annulus.
Trivial Annulus
A trivial annulus is a special case where the inner circle and outer circle coincide, resulting in a single circle. In this case, the width of the annulus is zero, and the area and circumference of the annulus are both zero. Below we present the generic diagram of a trivial annulus.
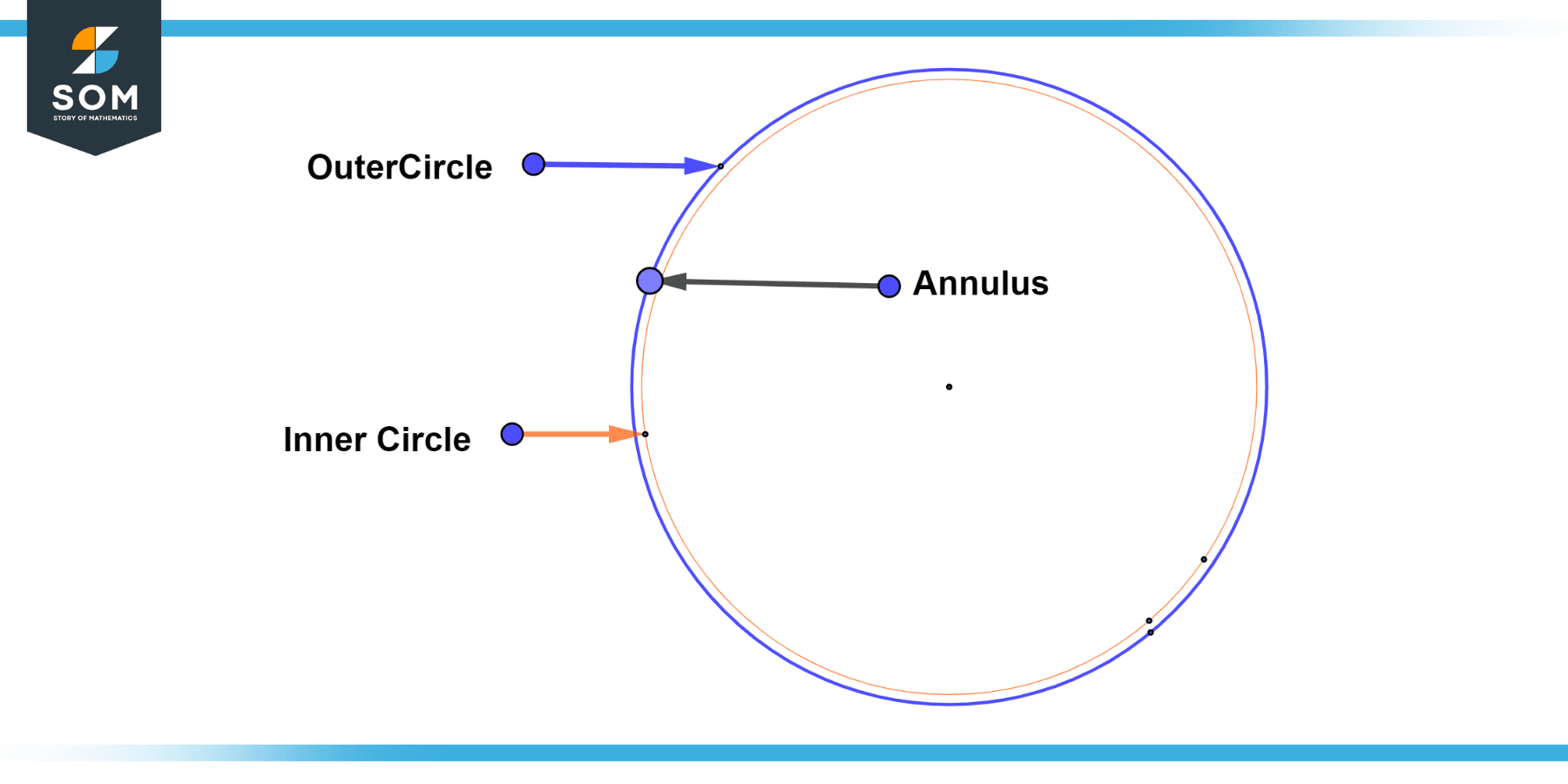
Figure-3: Trivial annulus.
Full Annulus
A full annulus, also known as a complete annulus, is an annulus where the inner circle has a radius of zero. This means that the inner circle is a single point at the center of the outer circle. The width of a full annulus is equal to the radius of the outer circle. Below we present the generic diagram of a full annulus.
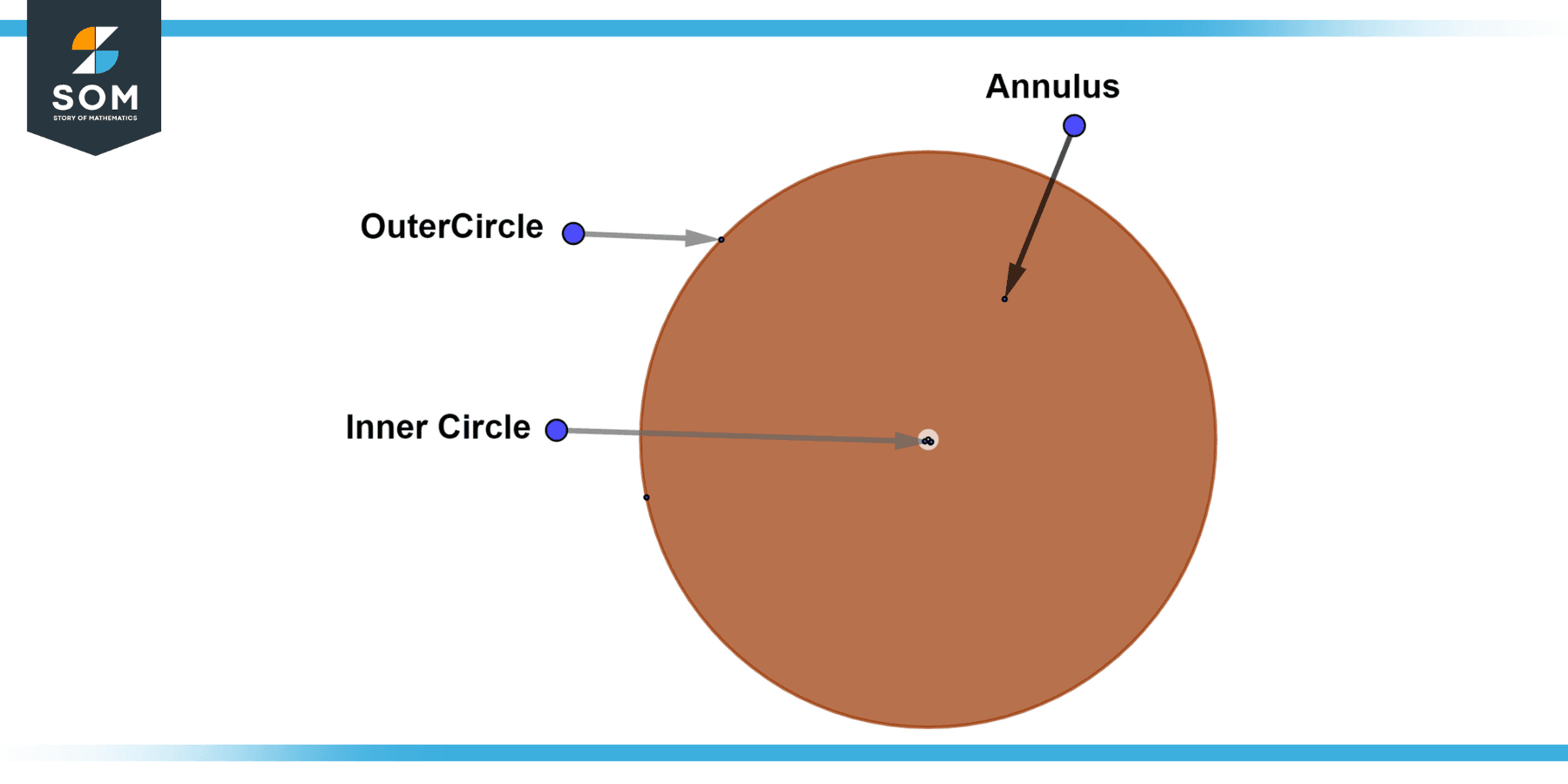
Figure-4: Full annulus.
Thin Annulus
A thin annulus is an annulus where the inner and outer circles’ radii are substantially different in size from the breadth. In other words, the difference between the radii is very small, resulting in a narrow band between the two circles. Below we present the generic diagram of a thin annulus.
Figure-5: Thin annulus.
Wide Annulus
A wide annulus is an annulus where the inner and outer circles’ radii are substantially different in size from the breadth. In this case, the difference between the radii is significant, resulting in a broader band between the two circles. Below we present the generic diagram of a wide annulus.
Figur-6: Wide annulus.
These types of annuli showcase different configurations and characteristics. Non-trivial annuli are the most common, while trivial annuli represent special cases. Full annuli have a zero radius for the inner circle, and the relative difference in widths distinguishes thin and wide annuli. Understanding these types helps analyze and work with annuli in various mathematical and practical applications.
Properties
Following are the properties of the annulus, a captivating geometric shape:
Concentric Circles
The annulus is characterized by two circles with the same center point. The larger circle is called the outer circle, while the smaller circle is called the inner circle.
Radius
The radius of the annulus is the distance from the center of the annulus to the center of the outer or inner circle. Let’s denote the radius of the outer circle as R and the radius of the inner circle as r.
Width
The distance between the radii of the outer and inner circles determines the annulus’ width. It is calculated as width = R – r.
Area
The annulus’ area is the difference between its inner and outer circles’ areas. The formula to calculate the area is A = πR² – πr² = π(R² – r²).
Circumference
The circumference of the annulus is the sum of the circumferences of the outer and inner circles. It is calculated as C = 2πR + 2πr = 2π(R + r).
Proportional Relationship
The area and circumference of the annulus are directly proportional to the difference in radii. As the width increases, the annulus’s area and circumference increase.
Symmetry
The annulus possesses radial symmetry, meaning that any line passing through its center divides it into two equal parts.
Relation to Sectors
The annulus can be seen as a collection of infinitely thin sectors, each with an infinitesimally small central angle. The sum of these sectors forms the annulus.
Understanding these properties is essential for working with annuli in various mathematical and real-world contexts. They allow for calculating areas, circumferences, and widths and exploring relationships between radii and concentric circles.
Ralevent Formulas
Following are the related formulas associated with the annulus:
Area Formula
An annulus’s area (A) can be calculated by subtracting the inner circle’s area from the outer circle’s area. The formula for the annulus area is given by A = πR² – πr² = π(R² – r²), where R is the radius of the outer circle and r is the radius of the inner circle.
Circumference Formula
An annulus’s circumference (C) can be found by adding the circumferences of the outer and inner circles. The formula for the circumference of the annulus is given by C = 2πR + 2πr = 2π(R + r), where R is the radius of the outer circle and r is the radius of the inner circle.
Width Formula
An annulus’s width (w) is the difference between the radii of the outer and inner circles. It can be calculated using the formula w = R – r, where R is the radius of the outer circle and r is the radius of the inner circle.
Outer Circle Radius Formula
If you know the width (w) and the radius of the inner circle (r), you can calculate the radius of the outer circle (R) using the formula R = r + w.
Inner Circle Radius Formula
If you know the width (w) and the radius of the outer circle (R), you can calculate the radius of the inner circle (r) using the formula r = R – w.
These formulas allow you to calculate various annuli-related quantities, such as the area, circumference, width, and radii. They provide the necessary tools to solve problems involving annuli in geometry and real-world scenarios. Understanding and utilizing these formulas can help you effectively analyze and work with annuli.
Applications
The annulus, a geometric shape consisting of the region between two concentric circles, finds applications in various fields due to its unique properties. Let’s explore some of the key applications of the annulus.
Architecture and Design
The annulus is often used in architectural designs to create aesthetically pleasing spaces. It can be seen in circular courtyards, gardens, and architectural elements. The annular shape adds visual interest and creates a sense of harmony and balance.
Engineering
In engineering, the annulus is frequently encountered in the design of mechanical components, such as bearings and seals. The annular space between rotating and stationary parts allows smooth rotation while maintaining separation and preventing leakage.
Physics and Optics
The annulus is relevant in studying optics and light diffraction. It is used to model phenomena like Fresnel diffraction patterns, where light waves passing through a circular aperture form concentric bright and dark rings. Understanding the properties of the annulus is crucial for analyzing and predicting these patterns.
Piping Systems
Annular shapes are employed in piping systems to create sealing and insulation. For example, in plumbing, annular gaskets ensure leak-proof connections between pipes, fittings, and valves.
Geophysics
In geophysics, annuli are utilized to model and study various geological phenomena. For instance, annular regions can represent geological layers or formations in subsurface modeling, aiding in the exploration and extraction of natural resources like oil and gas.
Mathematics
The annulus is a subject of study in mathematics, particularly in complex analysis. It plays a role in understanding the behavior of functions in complex plane regions and the concept of holomorphicity. The properties of the annulus are explored in relation to conformal mappings, contour integrals, and other mathematical techniques.
Data Analysis
In data analysis and statistics, the annulus can be utilized in clustering algorithms and pattern recognition tasks. Patterns and relationships between data points can be identified and analyzed by representing data points in a two-dimensional annular space.
Jewelry and Ornamentation
The annulus shape is popular in jewelry design, where it is used to create rings, bracelets, and other circular ornaments. The circular form of the annulus symbolizes eternity, unity, and the infinite, making it a meaningful choice for jewelry pieces.
Sports and Recreation
The annular shape is found in various sports equipment and recreational activities. For example, players aim to throw discs into annular targets with different radii in disc golf. The annulus is also seen in the design of archery targets and sports such as ring toss and horseshoe pitching.
Electronics
Annuli designs circular printed circuit boards (PCBs) in electronics. Circular PCBs with annular shapes allow for efficient component placement, improved signal integrity, and enhanced thermal management in electronic devices.
Medical Imaging
Medical imaging methods like computed tomography (CT) scans and magnetic resonance imaging (MRI) make use of angular forms. These imaging systems’ annular detectors or sensors help capture and analyze data, enabling detailed visualization of internal structures and assisting in medical diagnoses.
Wheels and Bearings
Annuli find application in the design of wheels and bearings. The annular shape of tires and wheel rims allows smooth rolling motion, while annular bearings provide rotational support and reduce friction in various mechanical systems.
These applications demonstrate the versatility and significance of the annulus across multiple fields. Its distinct geometry and properties make it a valuable practical, aesthetic, and theoretical shape.
Exercise
Example 1
Find the area of an annulus with an outer radius of 8 units and an inner radius of 4 units.
Solution
Using the annulus area formula, we have:
A = π(8² – 4²)
A = π(64 – 16)
A = 48π square units
Example 2
Find the circumference of an annulus with an outer radius of 10 units and an inner radius of 6 units.
Solution
We use the annulus circumference formula to have C = 2π(10 + 6) = 32π units.
Example 3
Find the width of an annulus with an outer radius of 12 units and an inner radius of 8 units.
Solution
Using the annulus width formula, we have w = 12 – 8 = 4 units.
Example 4
Find the outer radius of an annulus with a width of 6 units and an inner radius of 3 units.
Solution
Using the annulus outer radius formula, we have R = 3 + 6 = 9 units.
Example 5
Find the inner radius of an annulus with a width of 5 units and an outer radius of 11 units.
Solution
Using the annulus inner radius formula, we have r = 11 – 5 = 6 units.
Example 6
Find the area of an annulus with an outer radius of 9 units and an inner radius of 0 units (full annulus).
Solution
Since it is a full annulus, the area is equal to the area of the outer circle. Thus, the area is:
A = π(9²)
A = 81π square units.
Example 7
Find the circumference of an annulus with an outer radius of 7 units and an inner radius of 7 units (trivial annulus).
Solution
Since the inner and outer circles coincide, the circumference is equal to the circumference of either circle. Thus, the circumference is C = 2π(7) = 14π units.
Example 8
Find the area of an annulus with an outer radius of 5 units and an inner radius of 4 units.
Solution
Using the annulus area formula, we have:
A = π(5² – 4²)
A = π(25 – 16)
A = 9π square units
Example 9
Find the area of an annulus with an outer radius of 10 cm and an inner radius of 5 cm.
Solution
Using the formula for the area of an annulus, we have:
A = π(R² – r²)
A = π((10 cm)² – (5 cm)²)
A = π(100 cm² – 25 cm²)
A = π(75 cm²)
A ≈ 235.62 cm²
Example 10
Calculate the circumference of an annulus with an outer radius of 8 inches and an inner radius of 3 inches.
Solution
Using the formula for the circumference of an annulus, we have:
C = 2πR + 2πr
C = 2π(8 inches) + 2π(3 inches)
C = 16π inches + 6π inches
C = 22π inches
C ≈ 69.12 inches
All images were created with GeoGebra.
