A rhombus is a two-dimensional (or flat), closed shape with four equal-length straight sides such that the opposite angles are equal and the opposite sides are parallel to each other. In other words, it is a parallelogram with all four sides equal. A square is a type of rhombus where all the interior angles are right angles.
Figure 1 below shows a Rhombus.
Figure 1 – Representation of a rhombus.
Rhombus as Quadrilateral
A quadrilateral is a rhombus shape. It is a parallelogram with identical sides and diagonals connecting at 90 degrees. This is the rhombus’s most crucial characteristic. A rhombus resembles a diamond. As a consequence, it is sometimes referred to as a diamond.
A rhombus is a closed planar two-dimensional figure. Due to its distinguishing characteristics, it is classed as an unusual parallelogram and a quadrilateral. Because all of its sides have the same length, a rhombus also was known as just an equilateral quadrilateral.
The term ‘rhombus’ is derived from the ancient Greek term ‘rhombos,’ which refers to something that spins.
A quadrilateral is a closed polygon with four sides and four vertices enclosing four angles. The total of a quadrilateral’s internal angles equals 360 degrees. The quadrilateral is classified into six types:
Parallelogram
Rectangle
Kite
Trapezium
Rhombus
Square
Rhombus, Parallelogram, and Square
A rhombus is a particular parallelogram since it fulfills the definition of a rectangle as a trapezoid with a second pair of parallel sides. A rhombus, like a cube, has four equal sides. As a response, it’s often referred to as a diagonal square. Examine the picture below to see how the rhombus relates to the trapezoid & square.
Figure 2 below shows a difference in Rhombus, Parallelogram, and Square.
Figure 2 – Difference between a rhombus and other polygons.
Due to its four equal sides, a square is a specific example of a rhombus. All of the angles in a square were right angles. However, not all of the angles in a rhombus must be right angles. As a result, a rhombus containing right angles is a square.
As a result, we may conclude:
Parallelograms are all rhombi or rhombuses, although not all parallelograms are rhombuses.
Every rhombi or rhombus is not a square, but every square is a rhombus.
Three other names can also know a rhombus:
Lozenge
Diamond
Rhomb
Rhombus Angles
One thing to remember regarding a rhombus’ diagonal is that, despite bisecting one another at 90 degrees, the two diagonals crossed will be the same length.
For example, if a diagonal is 10 cm long and another diagonal bisects it, it is split into two 5 cm pieces. You can calculate the length of a diagonal if you know the side of a rhombus and the values of specific angles.
The following are some exciting rhombus angle facts:
The inner angles of a rhombus are four.
The total of a rhombus’ internal angles equals 360 degrees.
A rhombus’s opposing angles are congruent with each other.
The adjoining angles are extraneous.
Diagonals in a rhombus intersect at right angles.
The diagonals of both rhombi bisect these angles.
Figure 3 bellows shows the angles of a rhombus.
Figure 3 – Representation of rhombus and its angles.
A Rhombus’s Properties
A rhombus is referred to as a unique parallelogram since it possesses all of the features of a parallelogram. Two diagonals serve as symmetry lines in a rhombus.
A symmetrical axis is a distinct line that splits an item in half. It generates a reflecting surface image of the item’s two sides. A rhombus’ diagonals all have reflection symmetry.
Characteristics of a Rhombus
The characteristics of a rhombus are listed below:
The rhombus has equal sides on all sides.
A rhombus’s opposite sides are parallel.
A rhombus’s opposite angles are equal.
Diagonals in a rhombus intersect at right angles.
Diagonals bisect a rhombus’ angles.
The combination of two angles that are adjacent equals 180 degrees.
You will receive a rectangle when you link the midpoints of the sides.
When you combine the center point of half the diagonal, you obtain another rhombus.
There are also a few more advanced properties on its relationships with other geometrical shapes:
There cannot be a constraining circle around a rhombus.
There could be no engraved circle within a rhombus.
The midpoints of four sides will be linked to form a rectangle, and the length and breadth of a rectangle will be the value of a major diagonal, resulting in a rectangle with half the area of the rhombus.
Two congruent, evenly spaced triangles are generated when the longer diagonal equals one of the sides of a rhombus.
When the rhombus is rotated around any side as that of the axis of rotation, you will receive a cylindrical surface with a convex conical at one end and a concave cone at the other.
Whenever the rhombus is rotated about the line connecting the center point of the different sides as that of the axis of rotation, you will see a cylinder surface with concave cones on both ends.
When the rhombus revolves around the longer lateral axes of rotation, you will get solid with two cones joined to their bases. In this scenario, the greatest diameter of the block is equal to the rhombus’s shorter diagonal.
When the rhombus revolves around the longer diagonal as that of the axis of rotation, you will get a solid containing two cones linked to their bases. In this scenario, the greatest diameter of the block is equal to the rhombus’s longer diagonal.
The Rhombus Area
The rhombus’ area is the territory it covers in a 2-dimensional surface. The formula for area is the product of the rhombus’ diagonals divided by two. It can be written as:
\[ A = \dfrac{(d1 \times d2)}{2} \times \text{square units} \]
Example of a Rhombus
When they noticed a rhombus-shaped tile, Sam and Victor played hopscotch at the playground. Each side of a tile was ten units long. Can you assist Sam and Victor in determining the tile’s perimeter?
Solution
The tile’s length is ten units.
Because a rhombus has equal sides, all four sides were equivalent to 15 units.
In the fascinating realm of geometry, one of the key figures that garner attention is the Rhombus. This captivating quadrilateral, which may appear to be a slanted square at first glance, holds a unique position in the world of geometry. A rhombus is defined by several distinct properties that set it apart from other quadrilaterals. While it shares some characteristics with squares and rectangles, such as having four sides, the Rhombus has its own specific set of attributes that lend it both intrigue and utility in various fields, from architecture to mathematics and beyond.
This article aims to explore and understand this adaptable geometric design, its inherent properties, and the associated mathematical concepts.
Definition
A rhombus is a type of quadrilateral, a geometric shape with four sides, in which all four sides have the same length. This makes it a special type of parallelogram, one where not just the opposite sides but all sides are equal. Although the angles within a rhombus don’t have to be right angles, the opposite angles of a rhombus are always equal.
Additionally, the diagonals of a rhombus are not only perpendicular but also bisect each other, meaning each diagonal divides the other into two equal parts. This rich combination of properties makes the Rhombus a fascinating figure in the study of geometry. Below represent the geometric diagram of the rhombus.
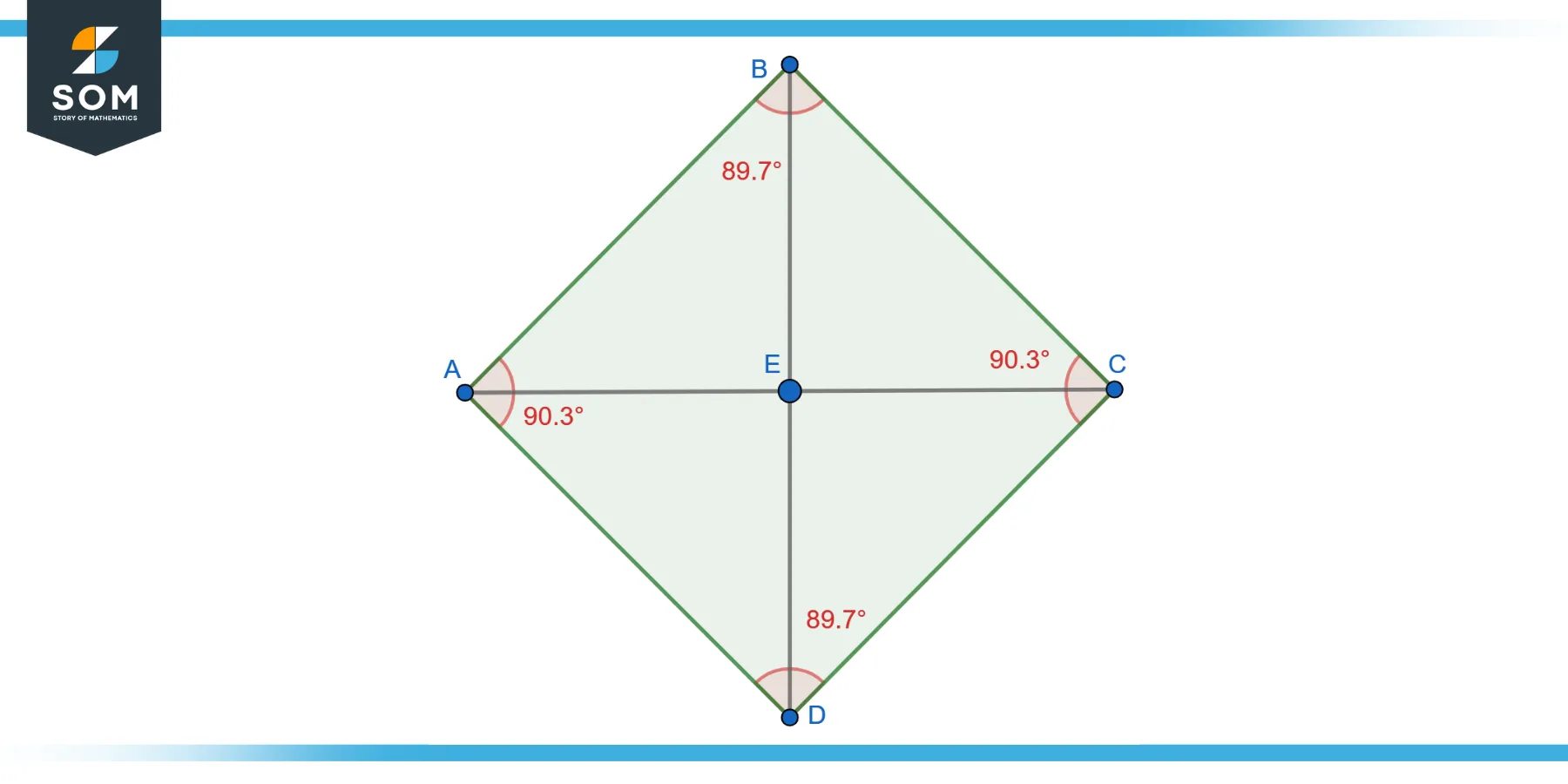
Figure-1: Generic rhombus.
Historical Significance
The Rhombus is a geometric shape with an intriguing historical background. Its history begins in ancient civilizations, when mathematicians and scholars first began to study the characteristics and significance of this unusual shape.
The concept of the Rhombus has been documented in various ancient cultures, including the Egyptians, Greeks, and Persians. In ancient Egypt, rhombuses were prominently featured in their architectural designs, hieroglyphs, and decorative arts. The Egyptians recognized the aesthetic appeal and symbolic value of the rhombus shape, incorporating it into their religious and cultural artifacts.
In ancient Greece, the Rhombus gained attention through the works of renowned mathematicians such as Pythagoras, Euclid, and Archimedes. Pythagoras, famous for his theorem on right triangles, recognized the Rhombus as a special case of a parallelogram with congruent sides. Euclid, in his influential book “Elements,” dedicated a section to the study of rhombuses, exploring their properties, diagonals, and relationship to other geometric shapes. Archimedes, known for his contributions to mathematics and physics, made advancements in the calculation of the Area and perimeter of rhombuses.
The Persians also demonstrated an appreciation for the rhombus shape in their art and architecture. Persian carpets, renowned for their intricate designs, often incorporate rhombus-shaped motifs as symbols of symmetry and balance. The rhombus motif can also be found in Persian tiles, mosaics, and calligraphy.
During the Renaissance period, the study of the Rhombus experienced a resurgence of interest. Artists, architects, and mathematicians drew inspiration from ancient Greek and Roman cultures, reintroducing rhombus-based designs into their works. In architecture, the Rhombus was utilized in the design of facades, ceilings, and decorative motifs, adding a sense of elegance and harmony to buildings.
In modern times, the Rhombus continues to be a significant shape in various fields, including mathematics, design, and engineering. Its symmetrical properties and balanced structure make it a useful tool for creating patterns, tessellations, and artistic compositions. In mathematics, the Rhombus serves as a foundation for exploring concepts like symmetry, congruence, and transformations. In engineering and construction, the rhombus shape finds practical applications in structural designs, building facades, and grid systems.
Understanding the historical background of the Rhombus allows us to appreciate its enduring influence in different cultures and its continued relevance in contemporary disciplines. The rhombus shape embodies both aesthetic beauty and mathematical precision, making it a captivating element in our world.
Types
A rhombus is a specific type of quadrilateral, and it doesn’t have subtypes like a quadrilateral does. All rhombuses share the same defining properties: they have four equal sides, their opposite sides are parallel, their opposite angles are equal, their diagonals bisect each other at right angles, and they are cyclic quadrilaterals (all vertices can lie on a single circle).
However, in more general or colloquial usage, people sometimes classify or refer to specific instances of rhombuses with additional characteristics using different terms. Here are the most common:
Square
A square is a specific type of Rhombus with additional properties. It is characterized by having all four sides of equal length and all four angles being right angles (90 degrees). The square’s diagonals are perpendicular to one another because of these right angles, dividing one another into equal pieces. A square is considered a special case of both a rhombus and a rectangle, as it possesses both characteristics. The equal side lengths and right angles make squares highly symmetrical and suitable for applications where equal lengths and right angles are essential, such as in tile patterns or building foundations. Below represent the geometric diagram of a square rhombus.
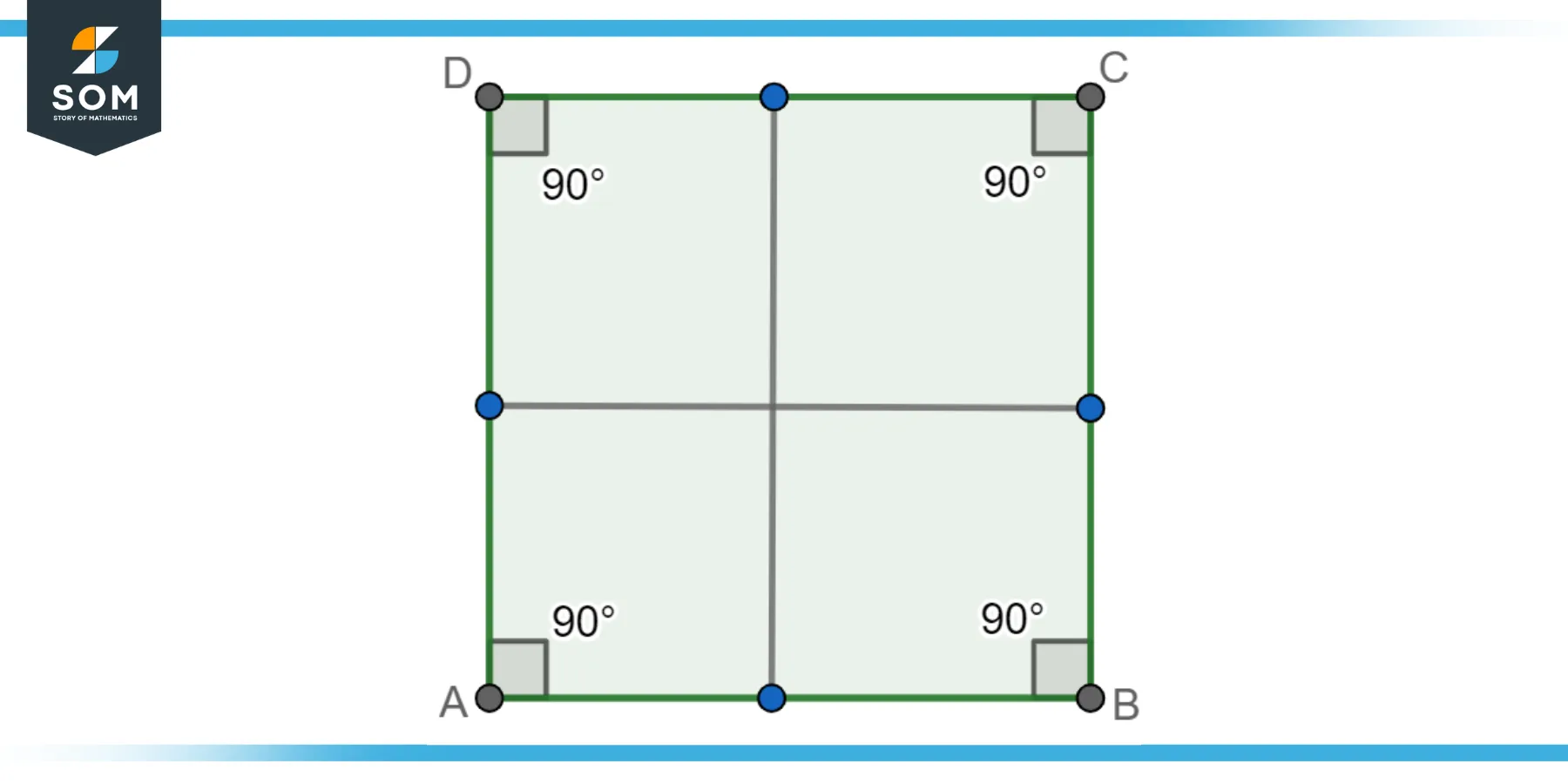
Figure-2: Square rhombus.
Diamond
In colloquial usage, a diamond is often used interchangeably with the term “rhombus”. However, in some contexts, a diamond refers to a tilted or rotated rhombus such that one pair of opposite angles is acute (less than 90 degrees) and the other pair is obtuse (greater than 90 degrees). This distinction arises when considering the orientation or presentation of the Rhombus. It is important to note that a diamond is typically synonymous with a rhombus in formal geometric terminology without implying any specific angle measurements or rotations. Below represent the geometric diagram of a diamond rhombus.
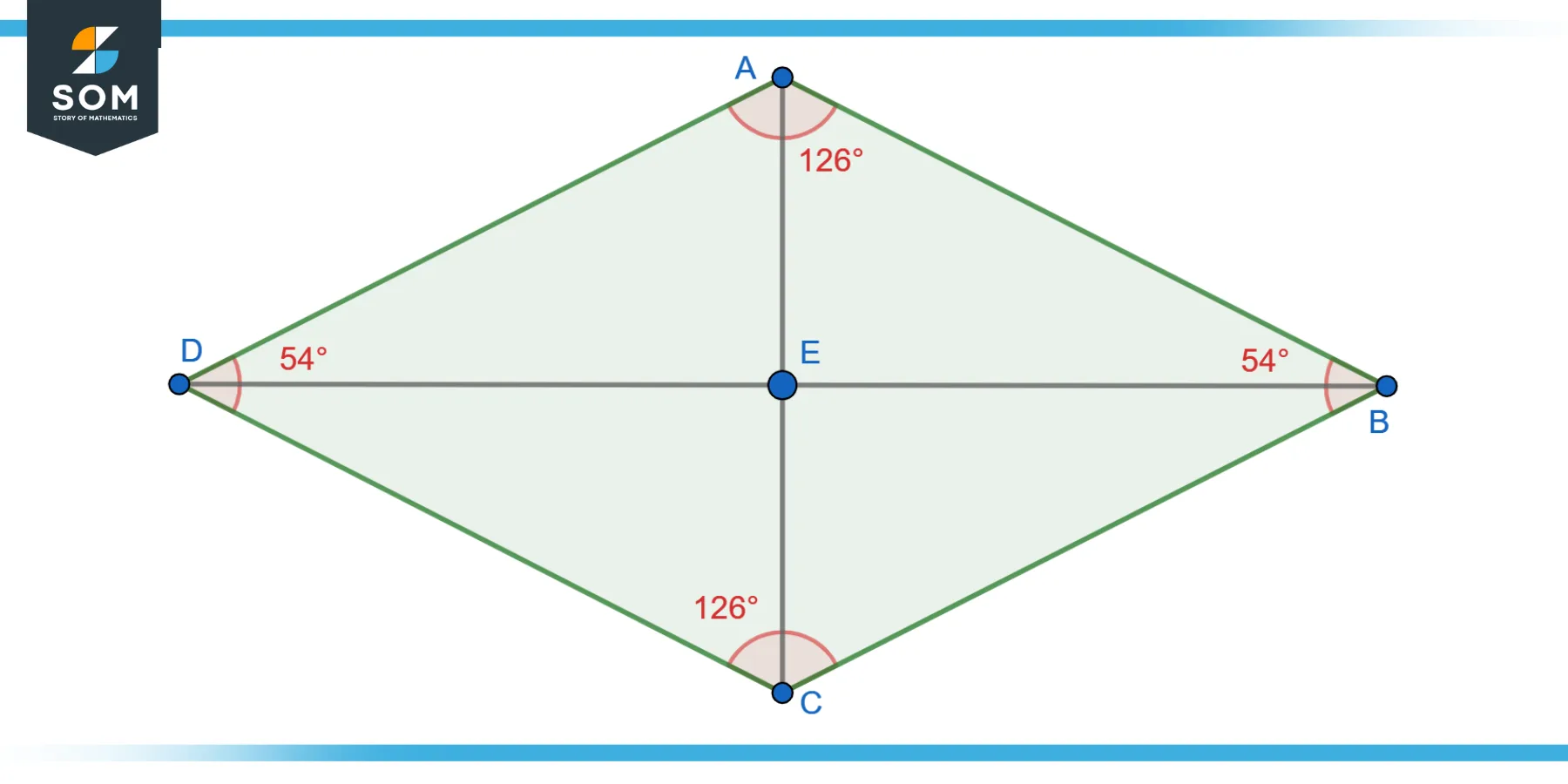
Figure-3: Diamnod rhombus.
Lozenge
The term lozenge is used in various contexts to refer to a rhombus with a specific orientation. In this case, a lozenge is a rhombus where one diagonal is horizontal. This implies that the other diagonal is vertical, perpendicular to the horizontal one. Like other rhombuses, a lozenge has four sides of equal length, and its opposite angles are congruent. The term “lozenge” is often used in fields such as heraldry, art, or jewelry design, where the shape is commonly employed and may have a specific aesthetic or symbolic connotation. Below represent the geometric diagram of the lozenge rhombus.
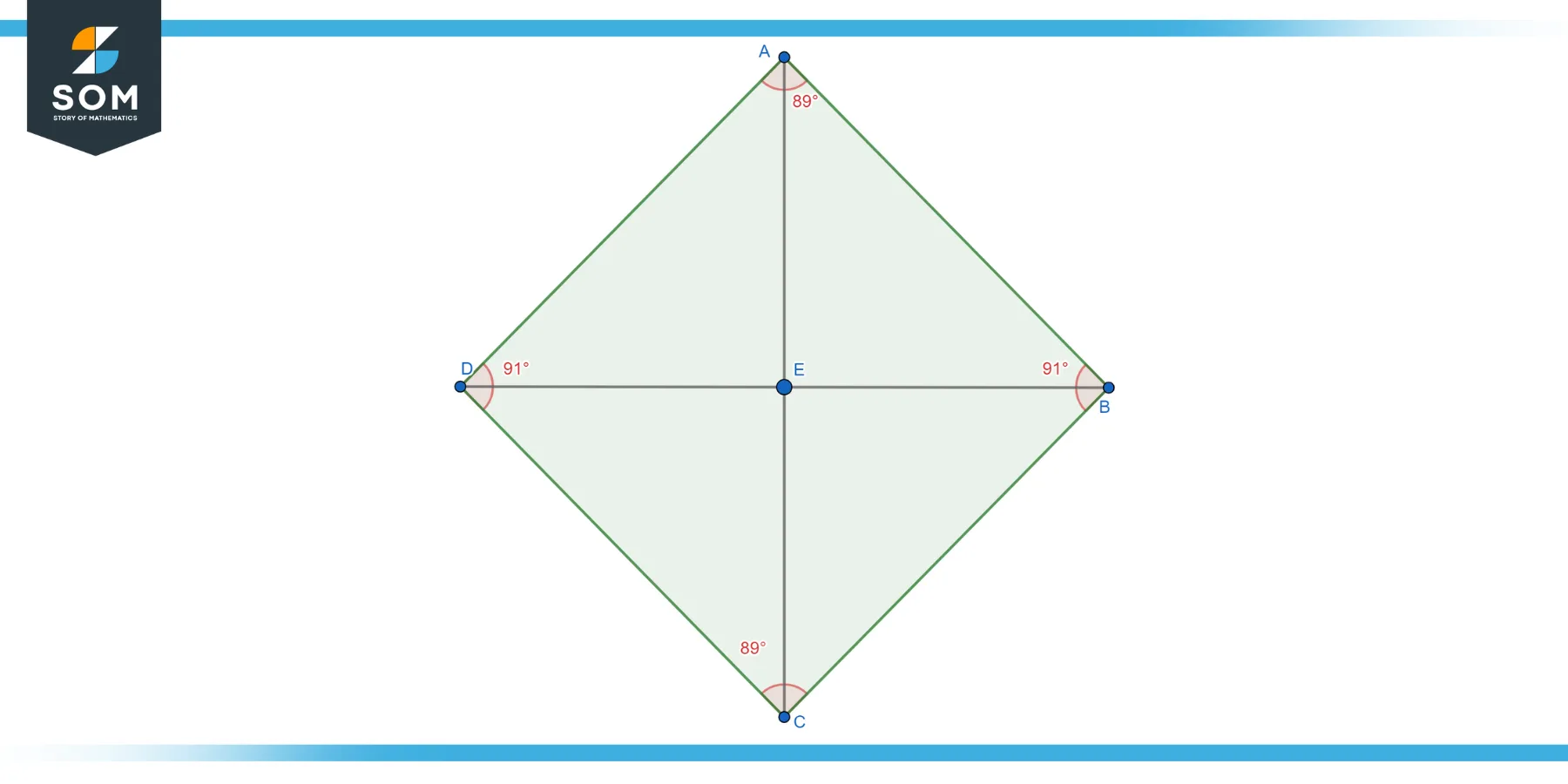
Figure-4: Lozenge rhombus.
It’s worth noting that while “square,” “diamond,” and “lozenge” are sometimes used to refer to specific instances of rhombuses with additional characteristics or orientations, in strict mathematical terminology, a rhombus is defined solely by having four sides of equal length. The other terms are more commonly used in informal or specialized contexts to describe variations or specific presentations of the rhombus shape.
While the Rhombus doesn’t have subtypes, it falls into these broader categories, each with its own distinct properties. A rhombus meets all the criteria for these types of quadrilaterals, underscoring its significant role in geometry.
Properties
Absolutely, let’s delve into the key properties of a rhombus:
All Sides Are Equal
This is the defining property of a rhombus. All four sides of a rhombus have the same length. This makes it a type of equilateral quadrilateral.
Opposite Sides Are Parallel
Just like any parallelogram, the opposite sides of a rhombus are parallel.
Opposite Angles Are Equal
The angles on opposite sides of a rhombus are always equal. This means if one angle measures 60 degrees, the angle directly across from it also measures 60 degrees.
Diagonals Perpendicular
The diagonals of a rhombus are perpendicular to each other, meaning they intersect at right angles.
Diagonals Bisect Each Other
The diagonals of a rhombus bisect each other, meaning they each divide the other into two equal parts.
Diagonals Bisect Angles
The diagonals of a rhombus bisect the angles of the Rhombus, creating two equal halves of each angle.
Sum of Angles
The sum of the interior angles of a rhombus is 360 degrees, like all quadrilaterals.
Cyclic Quadrilateral
A rhombus is a cyclic quadrilateral. This means all of its vertices can lie on a single circle.
These properties collectively give the Rhombus its unique geometric identity, differentiating it from other quadrilaterals and making it a topic of considerable interest in the field of geometry.
Ralevent Formulas
Certainly! Here are some key formulas related to the Rhombus:
Perimeter
The perimeter (P) of a rhombus is calculated as four times the length of one side (a). The formula is:
P = 4a
Area
The Area (A) of a rhombus can be calculated using the lengths of the diagonals (d1 and d2). The formula is:
A = 1/2 × d1 × d2
Length of Diagonals
If you know the side length (a) of the Rhombus and one of the angles (θ), you can find the lengths of the diagonals (d1 and d2) with these formulas:
d1 = a × √(2+2cosθ)d2 = a × √(2-2cosθ)
Angle
The measure of each angle (θ) can be found using the lengths of the diagonals (d1 and d2). The cosine of each acute angle is half the ratio of the difference in the squares of the diagonals to their sum:
cos(θ) = (d1² – d2²) / (d1² + d2²)
Radius of Inscribed Circle (Inradius)
The radius (r) of the circle that can be inscribed in a rhombus (also called the inradius) can be found using the Area (A) and the semi-perimeter (s = 2a). The formula is:
r = A / s
The Radius of Circumscribed Circle (circumradius)
The radius (R) of the circle that can be circumscribed around a rhombus (also called the circumradius) can be found using the diagonals (d1 and d2). The formula is:
R = 1/2 × √(d1² + d2²)
These formulas cover the majority of calculations you might need to perform related to a rhombus. They highlight the interconnections between the sides, diagonals, angles, and radii of the inscribed and circumscribed circles, underlining the rich geometric properties of this shape.
Applications
The Rhombus, as a geometric shape, finds diverse applications across various fields. It’s unique properties and symmetrical nature makes it a versatile tool in numerous disciplines. Let’s examine some of the main Rhombus uses in many disciplines.
Mathematics
In mathematics, the Rhombus serves as a fundamental shape for exploring various concepts. It is used to study properties such as angles, diagonals, and symmetry. Rhombuses are also employed in geometric proofs, tessellations, and transformations. The Rhombus provides a valuable example of a special type of quadrilateral with congruent sides.
Art and Design
The Rhombus plays a significant role in art and design. Its balanced structure and symmetry make it an appealing shape for creating patterns, mosaics, and tessellations. Rhombus-based motifs are utilized in various art forms, including painting, sculpture, textiles, and architecture. The Rhombus adds visual interest, rhythm, and harmony to artistic compositions.
Engineering and Architecture
In engineering and architecture, the Rhombus finds practical applications. Its inherent stability and strength make it suitable for structural designs, particularly in bridges and trusses. The rhombus shape is also utilized in facades, decorative elements, and grid systems, enhancing the aesthetics and functionality of buildings.
Navigation and Cartography
The Rhombus has historical significance in navigation and cartography. In early mapmaking, rhumb lines, also known as loxodromes, were used for navigation purposes. These lines form a series of interconnected rhombuses on navigational charts, helping sailors maintain a constant compass bearing during voyages. While modern navigation methods have evolved, the Rhombus remains a symbol of maritime exploration.
Crystallography and Material Science
In crystallography, the Rhombus is an important shape for understanding the arrangement of atoms in crystals. Rhombus-shaped unit cells are used to represent the repeating patterns found in crystal structures. The study of rhombus-based crystal lattices provides insights into the properties and behavior of materials in fields such as chemistry, physics, and material science.
Game Design and Puzzles
The rhombus shape indeed plays a significant role in game design and puzzles. It is often used as a building block for creating board games, tile-based puzzles, and recreational mathematics challenges. Rhombus-shaped game boards and puzzle pieces offer interesting gameplay mechanics and aesthetic appeal. They add a unique twist to the gameplay experience and provide opportunities for strategic thinking and problem-solving.
Biological Sciences
In biology, the rhombus shape can indeed be observed in various natural structures. For example, fish scales often exhibit a rhombus-like shape, providing both protection and flexibility. Rhombus-shaped cells or patterns can also be found in biological tissues and organisms, contributing to their overall form and function.
These are just a few examples of the wide-ranging applications of the Rhombus in different fields. Its geometric properties and symmetrical nature make it a versatile and practical shape, influencing disciplines ranging from mathematics and engineering to art and biology. The Rhombus’s significance extends across various domains, highlighting its importance and impact in the natural and man-made world.
Exercise
Example 1
Finding Perimeter
What is the perimeter of the rhombus given in Figure-5?
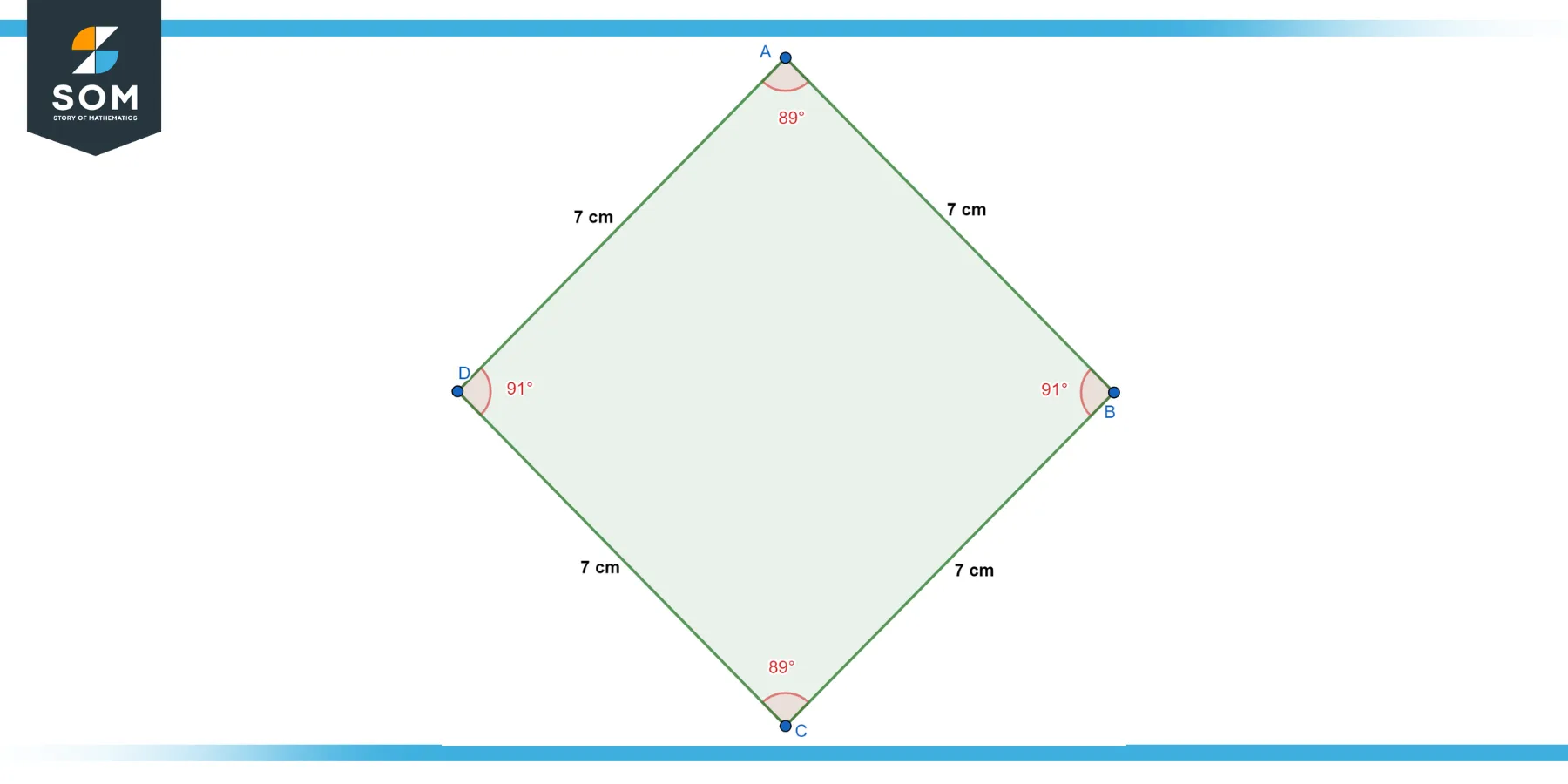
Figure-5.
Solution
The length of one side of a rhombus can be multiplied by 4 to determine its perimeter. Thus, the perimeter = 4 × 7 = 28 cm.
Example 2
Finding Area
Given a rhombus with diagonals measuring 12 cm and 16 cm, what is the Area?
Solution
The formula Area = 0.5 × d1 × d2, can be used to determine the area of a rhombus, where d1 and d2 are the diagonal lengths. Substituting the given values, we get Area = 0.5 × 12 × 16 = 96 cm².
Example 3
Finding Length of Diagonals
Suppose a rhombus has a side length of 9 cm and one angle measuring 60 degrees. Find the lengths of its diagonals.
Solution
The lengths of the diagonals can be calculated using the formulas:
d1 = a × √(2+2cosθ)
d1 = 9 × √(2 + 2cos60)
d1 ≈ 15.588 cm
d2 = a × √(2-2cosθ)
d2 = 9 × √(2 – 2cos60)
d2 ≈ 6.412 cm.
Example 4
Finding Angles
Given a rhombus with diagonals measuring 10 cm and 12 cm, find the measures of its angles.
Solution
The angles of a rhombus can be calculated using the formulas:
cosθ = (d1² + d2² – 2a²) / (2d1d2)
cosθ = (10² + 12² – 27²) / (210×12) ≈ 0.3, so θ
cosθ = arccos(0.3)
cosθ≈ 72.55 degrees.
Therefore, each angle of the Rhombus is approximately 72.55 degrees.
Example 5
Finding Inradius
Given a rhombus with an area of 48 cm² and a side length of 10 cm, what is the inradius (radius of the inscribed circle)?
Solution
The inradius of a rhombus can be calculated using the formula r = A / s, where A is the Area, and s is the semi-perimeter (half of the perimeter). The semi-perimeter of a rhombus is equal to half the perimeter, which is equal to half the sum of all four sides. In this case, the semiperimeter is s = 4 × (10/2) = 20 cm. Therefore, the inradius r = 48 / 20 = 2.4 cm.
Example 6
Diagonal Lengths Given Area and One Diagonal
If the Area of a rhombus is 60 cm² and one of its diagonals is 8 cm, what is the length of the other diagonal?
Solution
We can rearrange the formula for the Area of a rhombus to find the other diagonal length. Using the formula Area = 0.5 × d1 × d2, where d1 and d2 are the lengths of the diagonals, we can solve for d2:
d2 = 2 × (Area / d1)
d2 = 2 × (60 / 8)
d2 = 15 cm
Therefore, the length of the other diagonal is 15 cm.
Example 7
Finding Side Length Given One Diagonal and Angle
Suppose a rhombus has one diagonal measuring 14 cm and an angle of 45 degrees. Find the length of its sides.
Solution
We can find the side length using the formula a = d1 / √(2+2cosθ), where d1 is the diagonal and θ is the angle. Substituting the given values, we get a = 14 / √(2 + 2cos45) ≈ 7.57 cm. Hence, the length of each side of the Rhombus is approximately 7.57 cm.
Example 8
Finding Side Length Given One Diagonal and Angle
Given a rhombus with a side length of 12 cm and an angle of 60 degrees, what is its Area?
Solution
The formula can be used to determine the area of a rhombus: Area = a² sinθ, where a is the side length, and θ is the angle. Substituting the given values, we get Area = 12² × sin60 ≈ 62.35 cm². Therefore, the Area of the Rhombus is approximately 62.35 square cm.
