JUMP TO TOPIC

The quadrilateral square, a classic geometric figure, is a subject of fascination and in-depth study. As a special type of quadrilateral, a square carries unique properties that distinguish it from its geometric siblings. Renowned for its equal sides and right angles, a square is a figure of simplicity and a symbol of balance and uniformity. Every side of a square is of the same length, and every angle is a right angle or 90 degrees. This elegant simplicity belies a wealth of complexity and variety within mathematics and geometry, making the square an essential building block in these fields.
This article delves deeper into the properties, characteristics, and fascinating applications of the humble yet powerful square.
Definition
A quadrilateral square, or simply a square, is a four-sided polygon or quadrilateral where all four sides are of the same length and every angle is a right angle, which means each angle measures 90 degrees. Moreover, it’s also a rectangle because it has all the properties of a rectangle – namely, the sides on opposite sides are equal, and all angles are right angles. However, what makes a square special is that all its sides are equal, too. A square also possesses equal-length diagonals, and they bisect each other at right angles. In other words, a square is a kind of regular polygon – one in which all sides and angles are equal – but within the specific category of quadrilaterals. This perfect symmetry of attributes gives the square a central place in the world of geometry and beyond. Below is the geometric diagram of a quadrilateral square.
Figure-1: Quadrilateral square.
Historical Significance
The Quadrilateral Square is a geometric shape with a rich historical background. Ancient civilizations can be found to be its ancestors, where early mathematicians and architects explored the properties and significance of this unique shape.
The concept of the square has been documented in various ancient cultures, including the Mesopotamians, Egyptians, and Greeks. In Mesopotamia, for example, clay tablets dating back to around 2000 BCE show evidence of geometric knowledge, including calculations related to squares and their properties.
The Egyptians were known for their advanced understanding of geometry, particularly in relation to architecture and construction. The construction of perfect square angles was a fundamental aspect of their architectural practices. They used simple tools, such as Egyptian rope stretchers, to create right angles and ensure the accuracy of their structures. Squares played a vital role in their temple designs and city planning.
In ancient Greece, the square gained prominence through the works of mathematicians like Pythagoras, Euclid, and Plato. Pythagoras, famous for the Pythagorean theorem, recognized the square as a fundamental element in geometry. In his book “Elements,” Euclid explored the properties of squares, including their angles, diagonals, and relationship to other shapes. Plato considered the square one of the five Platonic solids, which were believed to have mystical significance.
During the Renaissance, the study of squares and other geometric shapes experienced a revival. Artists and architects like Filippo Brunelleschi and Leonardo da Vinci, drew inspiration from the ancient Greeks and Romans, incorporating square-based designs into their works. The use of squares in architectural elements, such as building facades and floor plans, became prevalent during this era, reflecting a revival of classical principles.
In modern times, the square remains a fundamental shape in mathematics, engineering, and various fields of study. Its symmetrical nature and well-defined properties make it a versatile and practical shape for diverse applications. Squares play a crucial role in many disciplines, from urban planning and architecture to computer graphics and scientific modeling.
Understanding the historical background of the Quadrilateral Square allows us to appreciate the enduring significance of this geometric shape. Its journey through ancient civilizations, classical antiquity, and modern-day applications showcases the timeless appeal and practicality of the square in our ever-evolving world.
Properties
Four Sides of Equal Length
A square is a quadrilateral with all four sides of the same length. This is often referred to as being ‘equilateral.’
Four Right Angles
Each interior angle of a square is a right angle, which means it measures 90 degrees. This makes the square a type of rectangle.
Diagonals are Equal
The diagonals of a square are of equal length. This is a distinctive property that sets it apart from many other quadrilaterals.
Diagonals Bisect Each Other
The diagonals of a square bisect each other, which means they cut each other in half at a 90-degree angle. This creates four smaller, congruent triangles within the square.
Diagonals Perpendicular to Each Other
Another important property of a square is that its diagonals are perpendicular to each other. This means they meet or intersect each other at right angles.
Perimeter and Area
The perimeter of a square (the total distance around the shape) is calculated as 4 times the length of a side, and the area (the total space within the square) is calculated as the side length squared.
Square as a Regular Polygon
As a regular polygon, a square has all sides and angles equal, providing it with a high level of symmetry.
Cyclic Quadrilateral
A square is a cyclic quadrilateral. This means all of its vertices can lie on a single circle.
Each of these properties plays an important role in the mathematical and geometric applications of squares, giving the square its unique characteristics and versatility in various fields.
Ralevent Formulas
Following are the key formulas related to a quadrilateral square.
Perimeter
The perimeter (P) is the total distance around the square. A square’s four sides are all the same length. Therefore, the perimeter is calculated by multiplying the length of one side by four. Formula: P = 4 × a (where ‘a’ represents the length of a side).
Area
Area (A) is the total space within the square. A square’s four sides are all the same length. Therefore, the area is calculated by squaring the length of one side. Formula: A = a².
Diagonal
The diagonal (d) is the line segment connecting any two non-adjacent vertices of the square. In a square, both diagonals are of equal length and can be calculated using the Pythagorean theorem. The diagonal of a square is the side length times the square root of 2. Formula: d = a × √2.
Relationship Between Area and Diagonal
The diagonal’s length can also be used to determine a square’s area. Given that the diagonal equals the side length times the square root of 2, the area can be found by squaring the diagonal length and dividing by 2. Formula: A = d² / 2 (where ‘d’ represents the diagonal length).
Inscribed Circle Radius
The radius (r) of an inscribed circle (a circle that fits perfectly inside the square) is half of the side length. Formula: r = a / 2.
Circumscribed Circle Radius
The radius of a circumscribed circle (a circle that passes through all vertices of the square) is half the length of the diagonal. Formula: R = d / 2.
These formulas allow us to calculate important properties of the square and also enable us to solve complex mathematical and geometric problems related to this special quadrilateral.
Types
The term “quadrilateral square” typically refers to a specific type of quadrilateral, the square. As such, there aren’t types of squares, per se. However, a square is a specific type of several broader categories of shapes. Each of these categories has specific properties that a square meets.
Quadrilateral
A square is a type of quadrilateral, which is a polygon with four sides. Other types of quadrilaterals include rectangles, parallelograms, rhombuses, trapezoids, and kites. Below is the geometric diagram of a quadrilateral square.
Figure-2: Quadrilateral square.
Parallelogram
A square is a specific type of parallelogram where all opposite sides are parallel. In a square, not only are the opposite sides parallel, but all sides are also of equal length, and all angles are right angles. Below is the geometric diagram of a parallelogram square.
Figure-3: Parallelogram square.
Rectangle
A square is a type of rectangle, which is a quadrilateral with four right angles. What makes a square distinct from other rectangles is that all of its sides are of equal length. Below is the geometric diagram of a rectangle square.

Figure-4: Rectangle square.
Rhombus
A square is a type of rhombus, which is a parallelogram with all sides of equal length. What makes a square special among rhombuses is that all its angles are right angles. Below is the geometric diagram of a rhombus square.
Figure-5: Rhombus square.
Regular Polygon
A square is a regular polygon. This is a polygon in which all sides and all angles are equal. In the case of a square, there are four sides, and each angle is 90 degrees. Below is the geometric diagram of a regular polygon square.
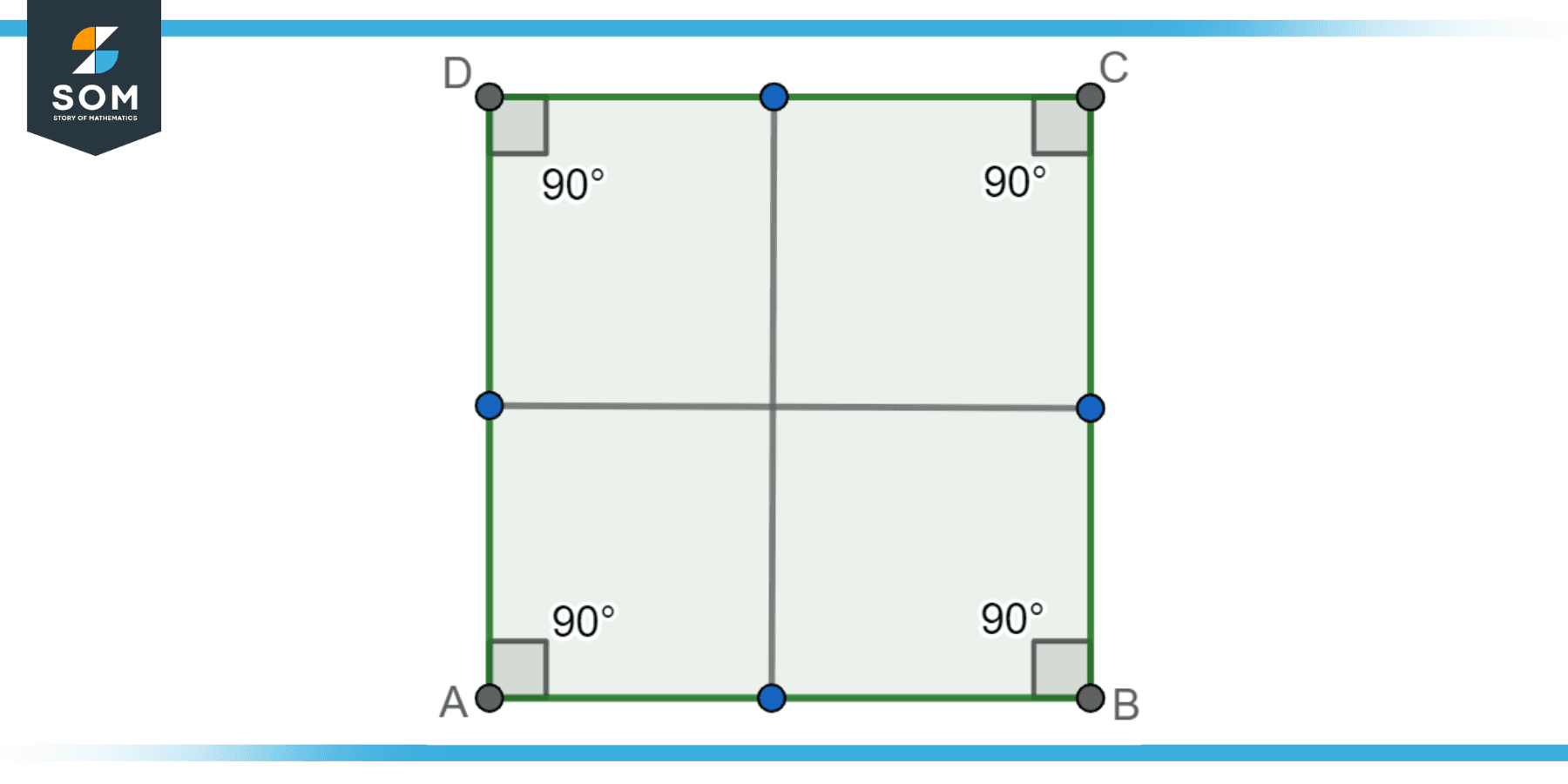
Figure-6: Regular polygon square.
Applications
The Quadrilateral Square, as a geometric shape, finds diverse applications across various fields. It’s unique properties and symmetrical nature makes it a versatile tool in numerous disciplines. Let’s explore some of the principal uses of the square in many disciplines:
Mathematics
In mathematics, the square serves as a fundamental building block for various concepts and calculations. It plays a central role in geometry, algebra, and trigonometry. The area and perimeter of a square are crucial measurements used in mathematical equations. Squares also feature prominently in geometric proofs and the study of symmetrical patterns.
Architecture and Construction
The square’s symmetrical and balanced structure makes it a favored shape in architecture and construction. It forms the basis for designing structures, floor plans, and layouts. Squares are often used to create proportional facades, courtyards, and rooms, providing stability and aesthetic appeal. They also serve as reference points for establishing right angles and aligning building elements accurately.
Engineering
Engineers frequently rely on squares for precise measurements and geometric calculations. In civil engineering, squares aid in surveying, layout planning, and the creation of infrastructure. Mechanical engineers utilize squares for machine designs, component alignments, and ensuring geometric accuracy. Electrical engineers use squares for circuit board designs and precise placement of components.
Computer Graphics and Design
The square plays a crucial role in computer graphics and design applications. It serves as a foundation for creating pixel-based images, providing a grid-like structure for rendering and manipulating visual elements. Squares are used in graphic design software to align objects, create patterns, and ensure visual harmony. They are also employed in the design of icons, logos, and user interfaces.
Physics and Scientific Modeling
Squares find applications in various scientific disciplines, particularly in the field of physics. Square-shaped objects or grids are used in experiments involving optics, diffraction, and interference patterns. In scientific modeling and simulations, squares are utilized to discretize space and analyze systems with a grid-like structure. They are also employed in the modeling of crystals and other regular patterns.
Urban Planning and Land Management
Squares play a significant role in urban planning and land management. Public squares, such as town squares or city plazas, serve as gathering places and focal points within communities. They provide open spaces for events, social interaction, and recreational activities. The layout of cities often incorporates square-shaped blocks for efficient land use and ease of navigation.
Puzzle Design and Recreational Mathematics
Squares feature prominently in puzzle design and recreational mathematics. Popular puzzles like Sudoku, magic squares, and sliding puzzles are based on square grids. The properties of squares, such as equal sides and right angles, make them ideal for creating engaging brain teasers and mathematical challenges.
These are just a few examples of the wide-ranging applications of the Quadrilateral Square in different fields. It’s geometric properties and symmetrical nature make it a fundamental shape with enduring practicality and relevance.
Exercise
Example 1
Finding the Perimeter
If the side length of a square (a) is 5 cm, what is its perimeter (P)?
Solution
The perimeter of a square is the sum of all its sides. As a square has four equal sides, The perimeter can be calculated by dividing the length of one side by four. Using the formula: P = 4 × a, we find that P = 4 × 5 = 20 cm. So, the perimeter of the square is 20 cm.
Example 2
Finding the Area
If the side length of a square (a) is 8 cm, what is its area (A)?
Solution
The area of a square is the amount of space inside it, which can be found by squaring the length of one side. Using the formula A = a², we find that A = 8² = 64 cm². So, the area of the square is 64 square cm.
Example 3
Finding the Diagonal
What is its diagonal (d) length for the square given in Figure-7?
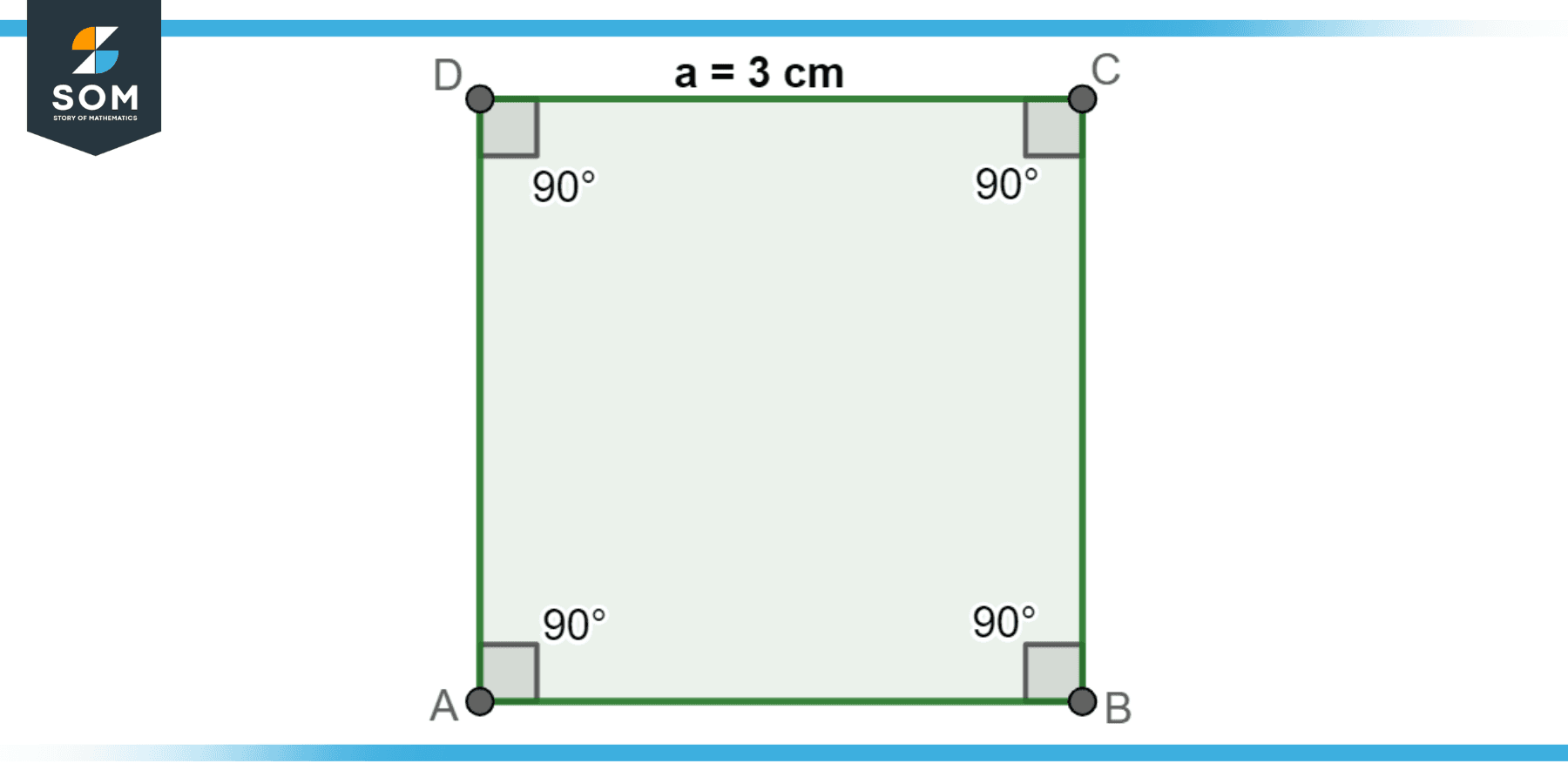
Figure-7.
Solution
The diagonal of a square is the line segment connecting any two non-adjacent vertices. It can be calculated using the Pythagorean theorem or, more simply, by multiplying the length of a side by the square root of 2. Using the formula d = a × √2, we find that d = 3 × √2 ≈ 4.24 cm. So, the length of the diagonal of the square is approximately 4.24 cm.
Example 4
Finding the Area From the Diagonal
If the diagonal length of a square (d) is 10 cm, what is its area (A)?
Solution
The area of a square can also be found by using the length of the diagonal. By squaring the length of the diagonal and then dividing by 2, we find the area. Using the formula A = d² / 2, we find that A = 10² / 2 = 50 cm². So, the area of the square is 50 square cm.
Example 5
Finding the Side Length From the Diagonal
If the diagonal length of a square (d) is 14 cm, what is its side length (a)?
Solution
The side length of a square can be found by dividing the length of the diagonal by the square root of 2. Using the formula a = d / √2, we find that a = 14 / √2 ≈ 9.90 cm. So, the length of the side of the square is approximately 9.90 cm.
Example 6
Finding the Side Length From the Area
If the area of a square (A) is 81 cm², what is its side length (a)?
Solution
The side length of a square can be found by taking the square root of the area. Using the formula a = √A, we find that a = √81 = 9 cm. So, the length of the side of the square is 9 cm.
Example 7
Finding the Inscribed Circle Radius
If the side length of a square (a) is 12 cm, what is the radius (r) of the inscribed circle?
Solution
The radius of an inscribed circle in a square (a circle that fits perfectly inside the square) is half of the side length. Using the formula r = a / 2, we find that r = 12 / 2 = 6 cm. So, the radius of the inscribed circle is 6 cm.
Example 8
Finding the Circumscribed Circle Radius
If the side length of a square (a) is 15 cm, what is the radius (R) of the circumscribed circle?
Solution
The radius of a circumscribed circle is half the length of the diagonal. First, we need to find the diagonal using the formula d = a × √2. So, d = 15 × √2 ≈ 21.21 cm. Then we use the formula R = d / 2 to find the radius of the circumscribed circle. Therefore, R = 21.21 / 2 ≈ 10.61 cm. So, the radius of the circumscribed circle is approximately 10.61 cm.
All images were created with GeoGebra.
