
In the enthralling realm of three-dimensional geometry, one shape stands out for its unique blend of beauty, symmetry, and mathematical intricacy: the Elliptic Paraboloid. This particular surface, characterized by its elliptical cross sections and parabolic form, is a fascinating study for mathematicians, engineers, architects, and artists alike. The elliptic paraboloid is not just a theoretical abstraction—it finds real-world applications in areas as diverse as antenna design, architectural structures, and optics.
This article explores the elliptic paraboloid, diving deep into its mathematical definition, geometric properties, related formulas, and examples that bring these concepts to life. Join us on this journey as we unravel the intriguing world of the elliptic paraboloid, a geometric marvel that encapsulates the elegance of mathematics in the tangible world.
Definition
The elliptic paraboloid is a smooth surface, and it is unbounded, meaning it extends indefinitely in one or two directions. It has a single point known as the vertex at the origin, which is the maximum or minimum point of the surface, depending on the orientation of the paraboloid.
The axis of symmetry of the elliptic paraboloid is the z-axis, and it possesses rotational symmetry around this axis. The surface is considered convex, as any line drawn between two points on the surface lies entirely on or within the surface.
This geometric shape, simple yet rich in its mathematical properties, is an important surface in many fields of study, ranging from mathematics to physics and engineering. Below we present generic diagrams for the elliptic hyperboloid.
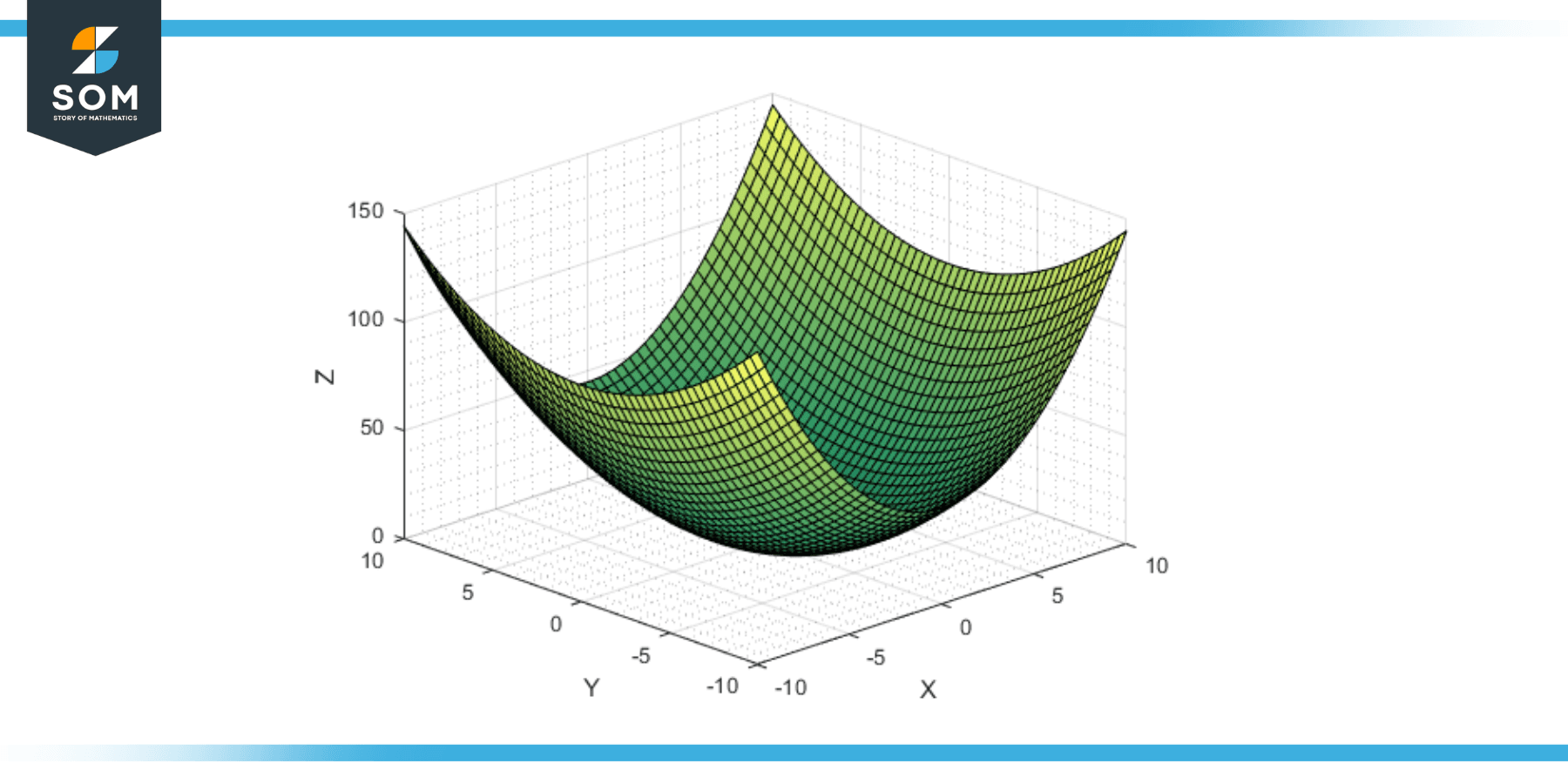
Figure-1: Generic elliptic hyperboloids.
Properties
The elliptic paraboloid is an intriguing geometric shape recognized by several distinct properties.
Parabolic Cross Sections
As the name suggests, an elliptic paraboloid has parabolic cross sections when cut parallel to either the xz-plane or the yz-plane. This feature gives it the “paraboloid” part of its name.
Elliptical Cross Sections
The resulting ellipse is formed when the elliptic paraboloid is cut parallel to the xy-plane (or the plane z = constant). This quality is what lends the “elliptic” part to its name.
Vertex
The elliptic paraboloid has a single point, the vertex, at the origin (0,0,0). This point is either the maximum or minimum of the surface, depending on the paraboloid’s orientation.
Axis of Symmetry
The z-axis serves as the axis of symmetry for an elliptic paraboloid. This means that the shape remains unchanged if rotated about the z-axis.
The direction of the Opening
Depending on the sign of the coefficients in its equation, an elliptic paraboloid can open upwards (when a and b are positive) or downwards (when a and b are negative).
Unbounded Surface
An elliptic paraboloid is an unbounded surface. This means that it extends indefinitely in its direction(s) of opening, giving it an infinite surface area.
Convex Shape
An elliptic paraboloid is a convex surface. Any line segment drawn between two points on the surface will lie entirely on or within the surface.
Smooth Surface
The elliptic paraboloid is a smooth surface, which means it has a well-defined tangent plane at each point and no sharp edges or vertices apart from the vertex of the paraboloid.
Single Sheet
An elliptic paraboloid is a single-sheeted surface, meaning it’s composed of one piece. It doesn’t intersect itself, and there are no discontinuities on the surface.
No Self-Intersections
Unlike some other quadric surfaces, the elliptic paraboloid has no self-intersections. It’s a simple, continuous surface that never crosses over itself.
Types
Upward Opening Elliptic Paraboloid
If the coefficients a and b in the standard equation of the elliptic paraboloid (z = ax² + by²) are positive, then the paraboloid opens upwards. It has its vertex at the origin (0,0,0), and the surface extends infinitely in the positive z direction. The cross sections parallel to the xz-plane and the yz-plane are upward-opening parabolas, and the cross sections parallel to the xy-plane are ellipses.
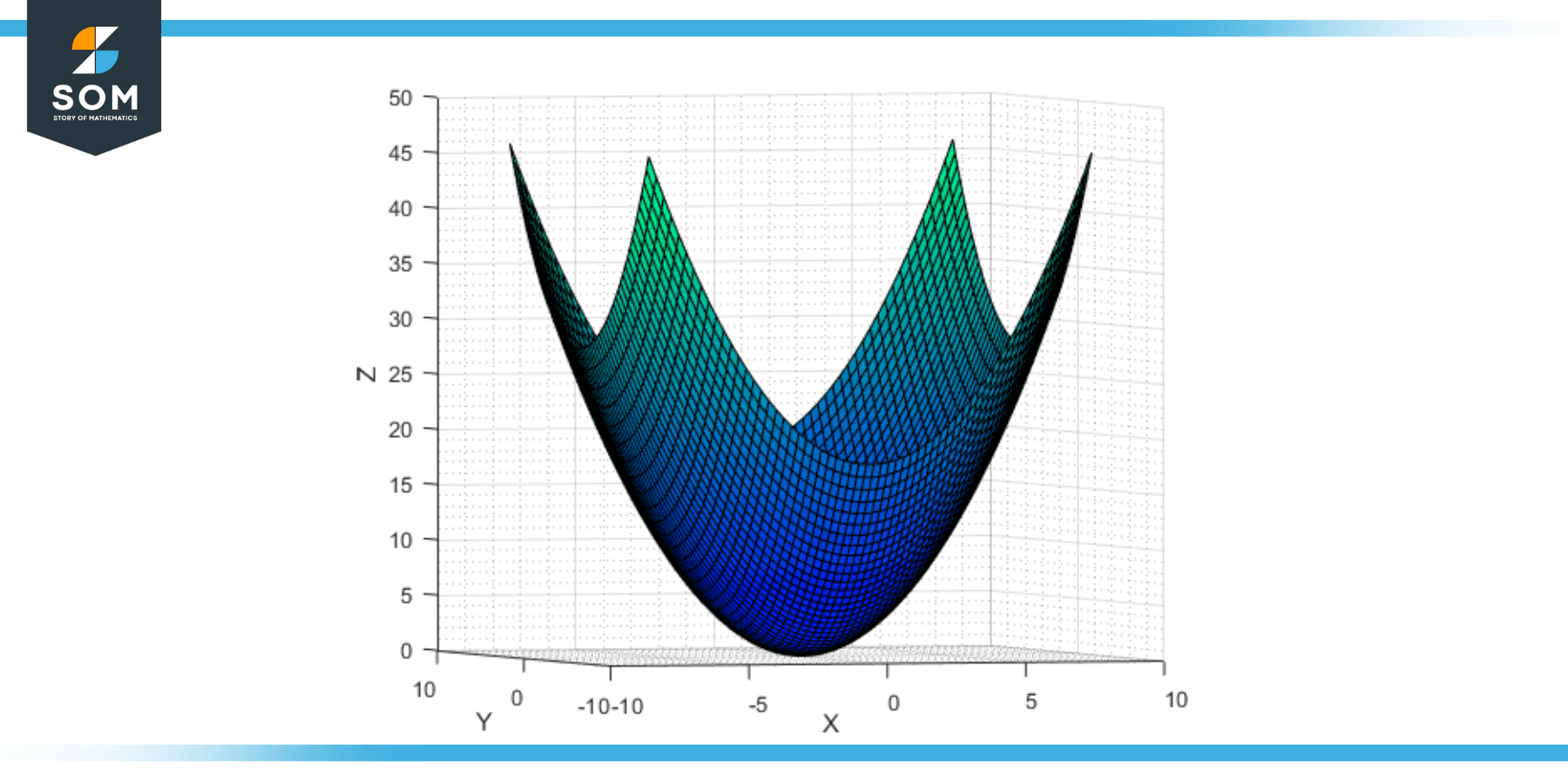
Figure-2: Elliptic hyperboloid upward opening.
Downward Opening Elliptic Paraboloid
If the coefficients a and b in the standard equation of the elliptic paraboloid (z = -ax² – by²) are positive, then the paraboloid opens downwards. It also has its vertex at the origin (0,0,0), but the surface extends infinitely in the negative z direction. The cross sections parallel to the xz-plane and the yz-plane are downward-opening parabolas, and the cross sections parallel to the xy-plane are ellipses.
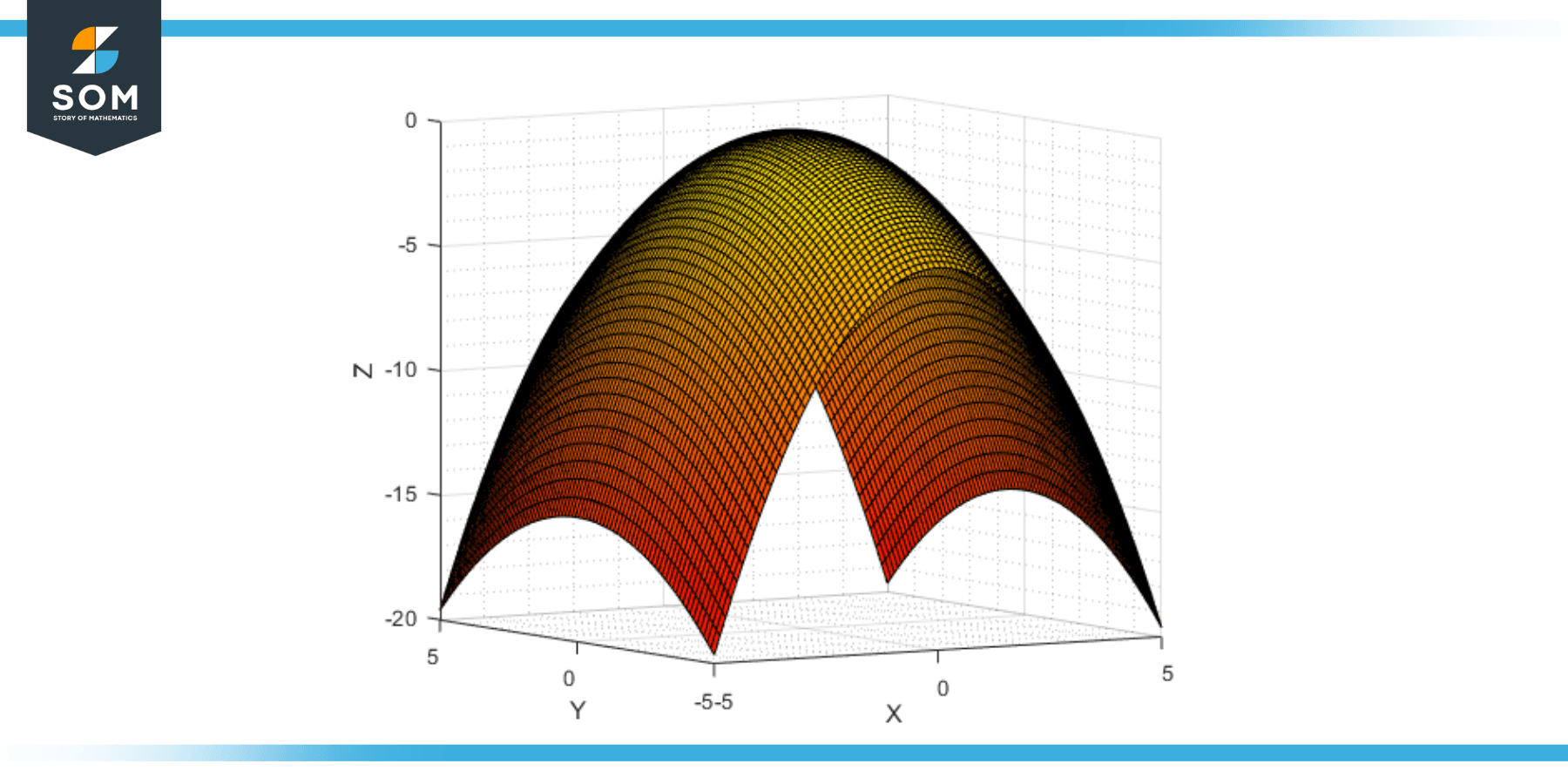
Figure-3: Elliptic hyperboloid downward opening.
Ralevent Formulas
The elliptic paraboloid is defined mathematically by its standard equation. It is a type of quadric surface, which means it is defined by a second-degree equation in three variables x, y, and z. Here are the key mathematical formulas related to the elliptic paraboloid:
Standard Equation
The standard form of the equation of an elliptic paraboloid is given by:
z = ax² + by²
or alternatively,
x²/a² + y²/b² = z
where a and b are positive constants, and x, y, and z are the variables representing coordinates in three-dimensional space. The values of a and b determine the “width” of the paraboloid in the x and y directions, respectively.
Vertex
The vertex of the elliptic paraboloid, given by the above equations, is always at the origin (0, 0, 0).
The direction of the Opening
The elliptic paraboloid opens upward if a and b are both positive in the standard equation and if a and b both are negative.
Foci
The elliptic paraboloid doesn’t have foci, unlike its related cousin, the ellipse. This is due to its unbounded nature in the z-direction.
Cross Sections
As discussed, the cross sections of an elliptic paraboloid parallel to the xz-plane or yz-plane are parabolas, and the cross sections parallel to the xy-plane are ellipses. These cross sections can be derived by setting either x, y, or z to a constant value in the standard equation and simplifying. For instance, if we set y = 0 in the standard equation, we get z = ax², which is the equation of a parabola. Similarly, if we set z = c (a constant), we get x²/a² + y²/b² = c, which is the equation of an ellipse.
Surface Area and Volume
Due to its unbounded nature, an entire elliptic paraboloid’s surface area and volume are infinite. However, for a given region of the paraboloid or a solid bounded by the paraboloid and a plane, one can compute the surface area and volume using multivariable calculus techniques, such as double or triple integration.
Applications
The Elliptic paraboloid finds diverse applications across various fields. Let’s explore some of its key applications:
Architecture and Design
The Elliptic paraboloid’s elegant and curved form makes it a popular choice in architectural design. It is frequently employed in constructing roofs, domes, arches, and other structural elements. The shape’s inherent stability, load-bearing capacity, and visually appealing profile contribute to its widespread use in historic and contemporary architecture.
Acoustics and Sound Reflection
The Elliptic paraboloid’s curved surface is well-suited for acoustic applications. Its shape aids in concentrating and directing sound waves, which is important for developing areas with desired sound diffusion and reflection qualities. Elliptic paraboloid surfaces are used in concert halls, theatres, and other performance spaces to improve acoustics.
Industrial Design and Product Development
The Elliptic paraboloid’s slender and flowing appearance has encouraged its incorporation into industrial design. It produces aesthetically beautiful and useful things like consumer goods, lighting fixtures, and furniture. The gentle curves of the shape add an organic and beautiful touch to product design.
Optics and Lighting
The Elliptic paraboloid’s shape has applications in optics and lighting design. It can create reflective surfaces that focus light or electromagnetic waves, such as reflector dishes and parabolic mirrors. Elliptic paraboloids are utilized in telescopes, satellite dishes, and other optical devices requiring precise light or signal concentration control.
Mathematics and Geometry Education
The Elliptic paraboloid serves as an educational tool in the field of mathematics and geometry. Its curved surface and parametric equations provide opportunities for studying concepts such as curvature, parametrization, and surface area.
Exercise
Example 1
Identifying an Elliptic Paraboloid
Given the equation: z = 4x² + y². Recognize that this equation is in the standard form of an elliptic paraboloid, z = ax² + by².
Solution
Here, a is 4, and b is 1. Since a and b are both positive, this elliptic paraboloid opens upwards. The vertex of the paraboloid is at the origin (0,0,0). The cross sections parallel to the xz-plane and yz-plane are parabolas, and the cross sections parallel to the xy-plane are ellipses.
Example 2
Cross Section of an Elliptic Paraboloid
Let’s consider the elliptic paraboloid given by the equation: z = 3x² + 2y². Find the equation of the cross-section of this paraboloid at z = 4.
Solution
To find the cross-section at z = 4, we substitute z = 4 into the equation of the paraboloid:
4 = 3x² + 2y²
We can rewrite this as:
x²/4/3 + y²/4/2 = 1
or
x²/4/3 + y²/2 = 1
This is the equation of an ellipse, which confirms that the cross-section of the paraboloid at z = 4 is an ellipse.
Example 3
The direction of Opening of an Elliptic Paraboloid
Consider the elliptic paraboloid defined by the equation: z = -2x² – 3y². Determine the direction in which the paraboloid opens.
Solution
The standard form of the equation of an elliptic paraboloid is z = ax² + by². In this equation, a is -2, and b is -3. Since both a and b are negative, the paraboloid opens downwards.
All images were created with GeoGebra.
