In the captivating world of geometry, the square pyramid stands as a symbol of structural balance and architectural beauty. Characterized by its distinctive four triangular faces converging to a single point, this geometric shape is a marvel of symmetry and dimensional harmony. With its square base providing a firm foundation, the square pyramid serves as a prime example of how simple geometric elements combine to create complex and aesthetically pleasing forms.

This article delves into the fascinating details of the square pyramid, exploring its properties, formulas, and applications in various fields. By the end of this exploration, you’ll have gained a comprehensive understanding of this captivating geometric figure.

Definition

A three-dimensional geometric shape belonging to the family of pyramids is called a square pyramid. This geometry has a square base and four triangle faces that come together at the vertex, also known as the apex. The lines connecting the apex to the vertices of the square base are known as the edges of the pyramid, and the point where an edge meets a face is termed a vertex.

In a square pyramid, the base and the apex are perpendicular to each other if you draw a line, also known as the height or altitude, from the apex to the center of the base. Noteworthy examples of square pyramids include the Great Pyramids of Egypt, showcasing this shape’s historical significance and enduring appeal. Below is the geometric diagram of a generic square pyramid.

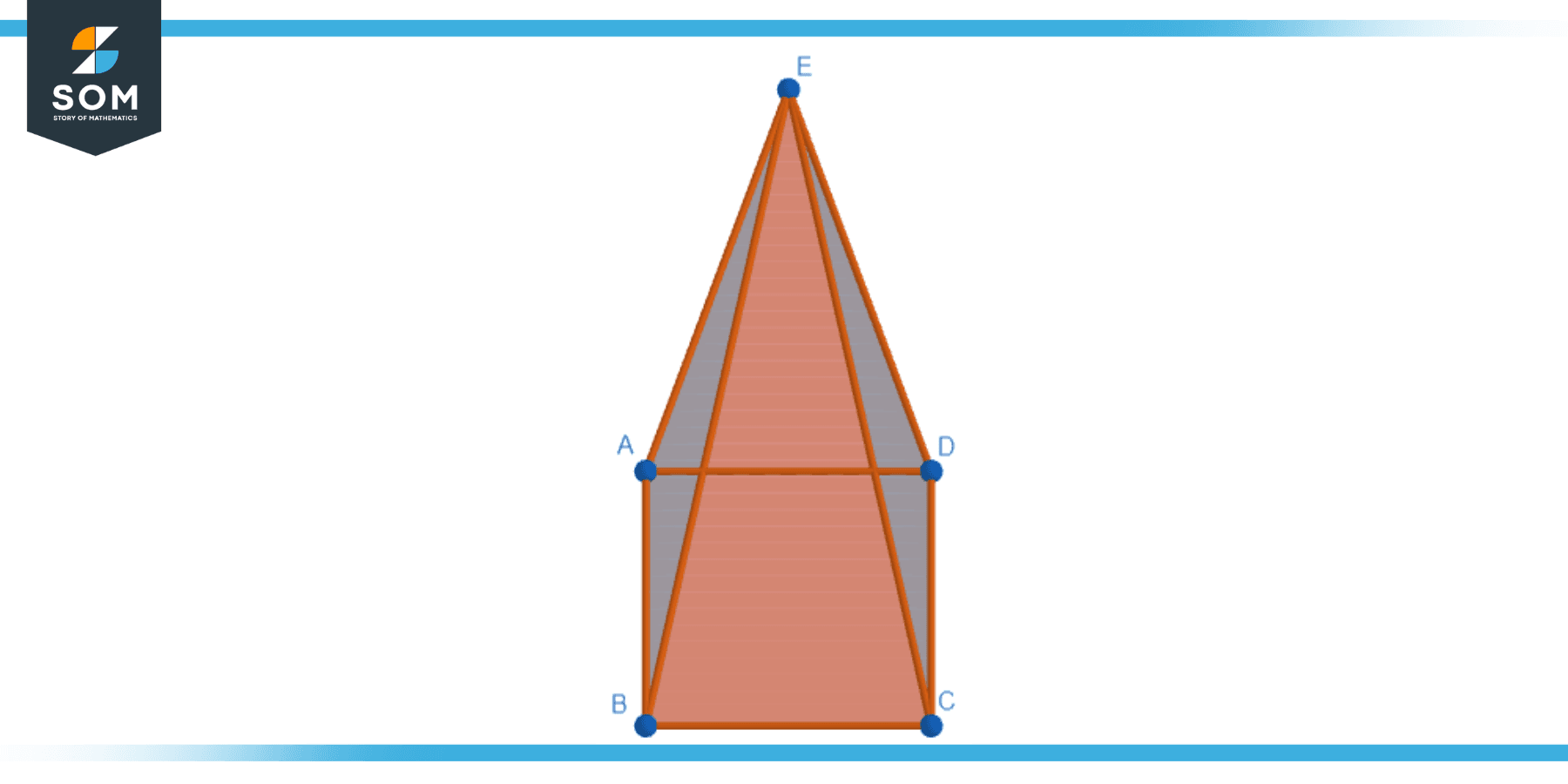
Figure-1: Generic square pyramid.

Historical Significance

The square pyramid, a captivating geometric shape, has a significant historical background that spans ancient civilizations. Exploring its origins provides insights into the evolution of geometry and its practical applications.

The study of geometry traces back to ancient civilizations, with notable contributions from the Egyptians, Babylonians, and Greeks. However, the concept of the square pyramid gained prominence during the time of the ancient Egyptians, who used it extensively in their architecture, particularly in the construction of pyramids.

The Egyptians, renowned for their monumental pyramids as tombs for their pharaohs, utilized the square pyramid as the fundamental shape for these awe-inspiring structures. The Great Pyramid of Giza, which was constructed approximately 2560 BCE, is a notable illustration of the use of the square pyramid. Its base forms a perfect square, and the four triangular faces converge to a single point at the apex, creating a majestic and symmetrical structure.

The Egyptians’ fascination with the square pyramid stemmed from their religious beliefs and the concept of the afterlife. They considered the pyramid to be a symbol of the sun god Ra’s rays and the pharaoh’s ascent to the heavens after death. The precise construction of square pyramids showcased the Egyptians’ advanced mathematical and engineering skills.

Beyond Egypt, the study of geometry expanded in ancient Greece. Greek mathematicians, including Euclid, extensively explored the properties of various geometric shapes, including pyramids. Euclid’s influential work, “Elements,” documented the principles of geometry around 300 BCE, covering the properties and characteristics of square pyramids.

During the Renaissance, the study of geometry and its practical applications experienced a resurgence. Architects and artists drew inspiration from ancient works and incorporated geometric shapes, including the square pyramid, into their designs. The symmetrical and aesthetically pleasing nature of the square pyramid made it an attractive element in architectural compositions, sculptures, and decorative art forms.

In modern times, the square pyramid continues to be a subject of mathematical study and finds applications in various fields. Mathematicians explore its properties, such as volume, surface area, and spatial relationships, while architects and engineers incorporate it into structural design, creating iconic buildings and monuments.

The historical background of the square pyramid is a testament to its enduring significance. From its origins in ancient Egypt to its influence on architecture and mathematics, the square pyramid represents a convergence of art, science, and culture. Its timeless appeal continues to captivate minds and serve as a reminder of humanity’s fascination with geometry and the pursuit of architectural excellence.

Types

In the study of geometry, the square pyramid, defined by its square base and four triangular faces, primarily appears in two forms:

Right Square Pyramid

A square pyramid is classified as a right pyramid when the line drawn from its apex is perpendicular to its base at the centroid. In other words, the apex lies directly above the center of the square base in a right square pyramid. This pyramid’s apex is aligned with the vertical axis of symmetry, meaning the pyramid appears the same from any direction when viewed from above. Below is the geometric diagram of a generic right square pyramid.

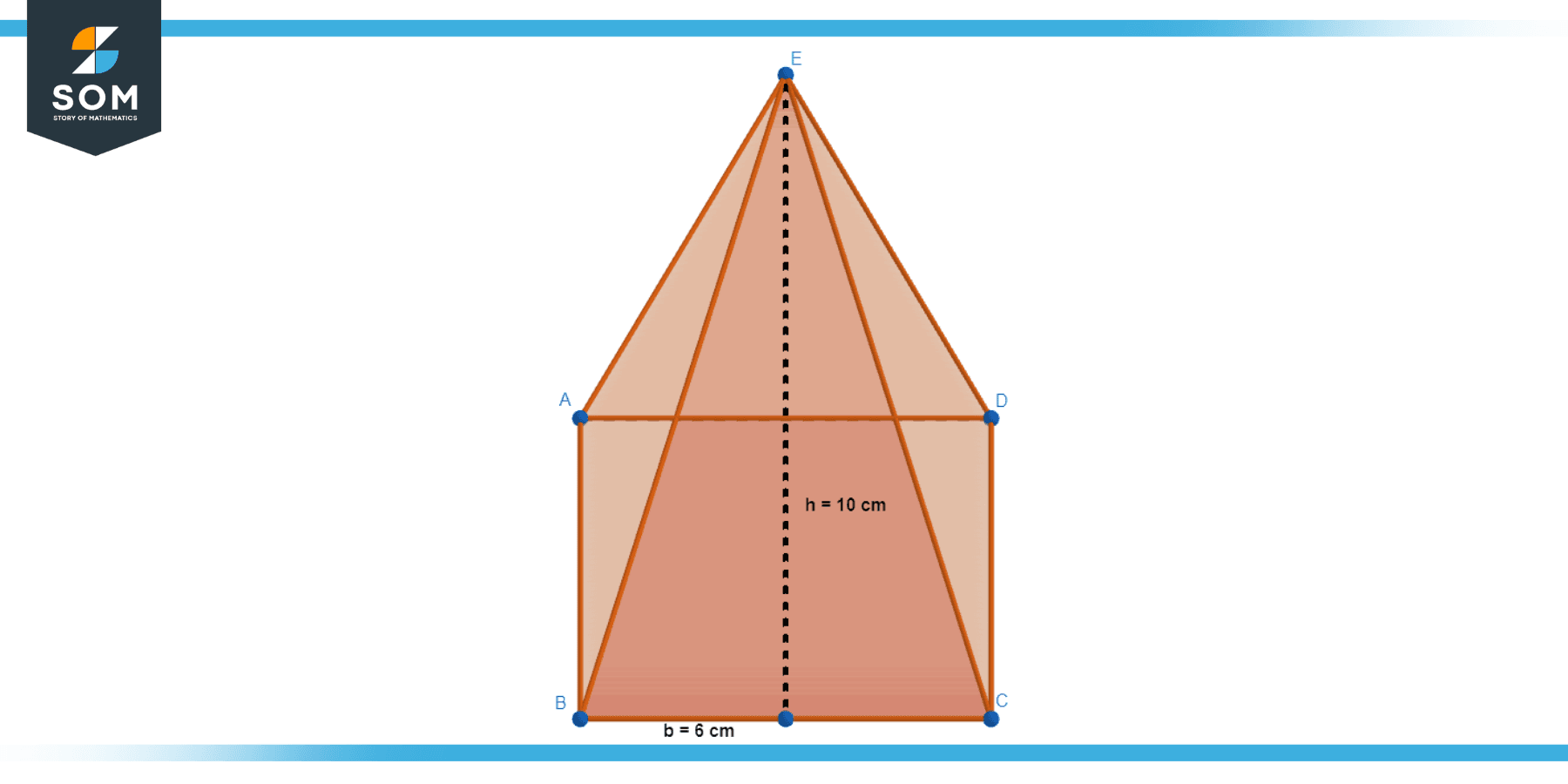
Figure-2: Right square pyramid.

Oblique Square Pyramid

When the apex does not lie directly above the center of the base, the pyramid is referred to as an oblique square pyramid. This pyramid’s apex is not aligned with the vertical axis of symmetry, resulting in an asymmetric appearance when viewed from above. Below is the geometric diagram of a generic oblique square pyramid.

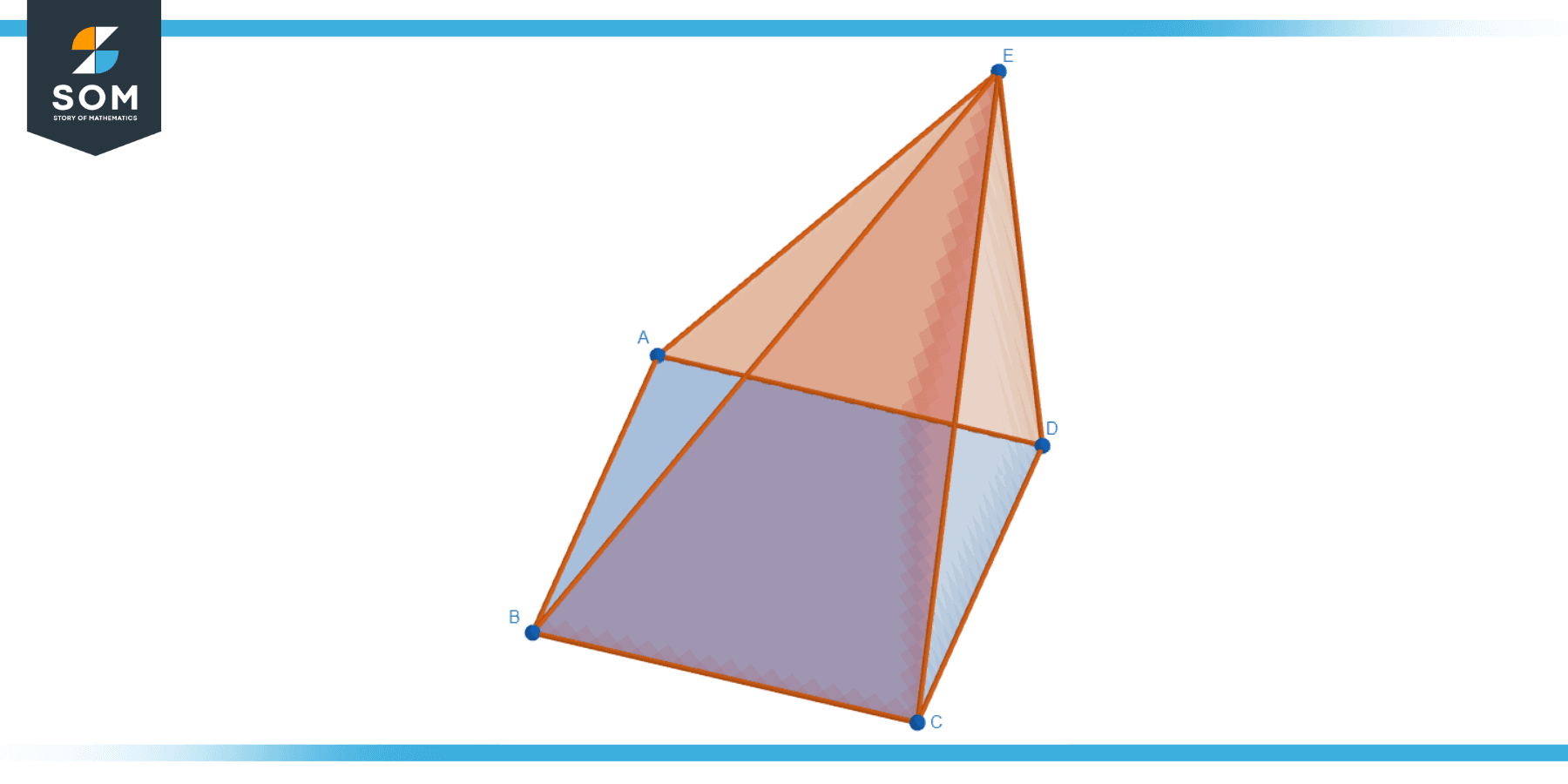
Figure-3: Oblique square pyramid.

While the base of the square pyramid remains constant (a square), the location of the apex changes, giving us these two main types of square pyramids. Regardless of the type, square pyramids continue to intrigue mathematicians and architects due to their combination of simplicity and symmetry.

Properties

The square pyramid, an interesting geometric shape, possesses several distinctive properties. Let’s dive into these geometric features:

Faces

 A square pyramid has five faces. The base is a square, and the other four faces are equilateral triangles in the case of a right square pyramid. These triangular faces meet at a single point, called the apex or vertex.

Edges and Vertices

The square pyramid has eight edges – four around the base and four connecting the base to the apex. It also has five vertices – four at the corners of the base and one at the apex.

Right and Oblique Pyramids

As noted earlier, there are two types of square pyramids. In a right square pyramid, the height, or line connecting the apex and base, is parallel to the base. The peak of an oblique square pyramid is not positioned over the middle of the base.

Symmetry

A right square pyramid has a high degree of rotational symmetry. When viewed from above, it looks the same from any direction. It also has reflection symmetry through a plane that includes the apex and two diagonally opposite corners of the base.

Base Diagonals

The diagonals of the square base are equal in length and bisect each other at 90 degrees. They are also equal to the height of the triangular faces.

Slant Height

The slant height is the height of each triangular face. It is the distance along the edge from the apex to the midpoint of a side of the base. In a right square pyramid, the slant height can be found using Pythagoras’ theorem if the edge length of the base and the height of the pyramid are known.

Understanding these properties of the square pyramid can prove useful in a variety of mathematical, architectural, and practical contexts.

Ralevent Formulas 

The square pyramid, a geometric shape, is associated with several mathematical formulas that allow us to calculate its important properties. Here are the key formulas related to the square pyramid.

Volume

The volume V of a square pyramid can be calculated using the formula V = 1/3 × B × h, where B represents the area of the base and h denotes the height of the pyramid.

Surface Area

The total surface area A of a square pyramid is calculated using the formula A = B + 1/2 × P × l, where B is the area of the base, P is the perimeter of the base, and l is the slant height.

Base Area

The area of the base B of a square pyramid is found by the formula B = a², where a is the length of a side of the base.

Base Perimeter

The perimeter P of the base is calculated by the formula P = 4 × a, where a is the length of a side of the base.

Lateral Area

The lateral area of a square pyramid, which includes the areas of the triangular faces only, is found by the formula L = 1/2 × P × l, where P is the perimeter of the base and l is the slant height.

Slant Height

In a right square pyramid, the slant height l can be found using the Pythagorean theorem: l = √(h² + (a/2)²), where h is the pyramid’s height, and a is the length of a side of the base.

These formulas help in comprehending the geometric properties of a square pyramid, as they provide a mathematical perspective to the shape’s structure, volume, and surface area. They are applicable in a range of scenarios, from solving complex mathematical problems to designing architectural structures.

Applications 

The square pyramid, with its unique geometric properties, finds applications in various fields, showcasing its versatility and practicality. Let’s explore some key applications:

1Architecture and Construction

The square pyramid’s distinct shape and symmetrical properties make it an appealing design element in architecture. It can be incorporated into building facades, interior spaces, and decorative elements to create visually striking structures.

Mathematics and Geometry Education

The square pyramid serves as an educational tool to teach and understand geometric concepts. It helps students grasp the principles of polyhedra, surface area, volume, symmetry, and spatial relationships

Sculpture and Art

Artists and sculptors often draw inspiration from the square pyramid’s form and use it as a creative element in sculptures, installations, and artistic compositions. Its symmetrical and geometric nature adds aesthetic appeal to art forms.

Industrial Design and Product Development

The square pyramid’s design principles find applications in industrial design. It can be used as a foundation for creating product prototypes, packaging, and decorative objects.

Archaeology and History

The square pyramid holds significance in archaeology and history, particularly in the context of ancient civilizations like the Egyptians. It provides insights into their architectural achievements, burial practices, and religious beliefs.

Computer Graphics and 3D Modeling

In computer graphics and 3D modeling, the square pyramid serves as a fundamental geometric shape. It is used to create complex 3D models, virtual environments, and simulations.

Industrial Engineering and Manufacturing

The square pyramid’s structural stability and symmetrical design make it useful in engineering applications. It can be utilized as a stable base or support structure in various industrial and manufacturing processes.

Mathematics and Mathematical Research

The square pyramid is of interest in mathematical research and exploration. Mathematicians study its properties, relationships with other geometric shapes, and its role in broader mathematical concepts.

Packaging and Design

The square pyramid shape is used in packaging design, such as tetra packs used for beverages. This shape provides a unique aesthetic while ensuring the efficient use of materials.

Physics and Chemistry

The square pyramid shape is also relevant in the fields of physics and chemistry, particularly in the study of crystal structures and molecular geometry. Some molecules, like the PCl5 (Phosphorus Pentachloride), adopt a square pyramidal structure.

Astronomy

The layout of certain constellations and star patterns can resemble a square pyramid. For example, the constellation Delphinus is sometimes described as a celestial square pyramid.

Data Visualization

Square pyramids can be used in graphs and charts to represent hierarchical data or processes that have multiple steps or levels. For example, in a pyramid chart, each level of the pyramid might represent a different category of data.

Environmental Design

In designing landscapes or garden elements, a square pyramid shape (as seen in topiaries and hedges) can be used to create visual interest and structural diversity.

These are just a few examples of the diverse applications of the square pyramid across different fields. Its unique geometry, symmetrical properties, and stability make it a valuable shape in architecture, design, education, and beyond. The square pyramid continues to inspire innovation and creativity in various disciplines, showcasing the enduring relevance of geometric shapes in practical applications.

Exercise 

Example 1

Volume Calculation

Calculate the volume of a square pyramid given in Figure-4.

Solution

The volume V of a square pyramid is given by:

V = 1/3 × B × h

Here, B = a² = 6² = 36 cm², and h = 10 cm,

so

V = 1/3 × 36 × 10

V = 120 cm³

Example 2

Surface Area Calculation

Calculate the surface area of a square pyramid with a base side length of 4 cm and a slant height of 5 cm.

Solution

First, calculate the base area B = a² = 4² = 16 cm². The surface area A of a square pyramid is given by:

A = B + 1/2 × P × l

Here, P = 4a = 4 * 4 = 16 cm, and l = 5 cm,

so

A = 16 + 1/2 ×  16 × 5

A = 56 cm²

Example 3

Slant Height Calculation

Calculate the slant height of a right square pyramid with a base side length of 3 cm and a height of 4 cm.

Solution

The slant height l of a right square pyramid is given by:

l = √(h² + (a/2)²)

Here, a = 3 cm and h = 4 cm,

so

l =√(4² + (3/2)²)

I = 4.6 cm

Example 4

Base Side Length Calculation

Find the base side length of a square pyramid given that its volume is 80 cm³ and its height is 8 cm.

Solution

The volume V of a square pyramid is given by:

V = 1/3 × B× h

so

B = V / (1/3 × h).

Here, V = 80 cm³ and h = 8 cm

so

B = 80 / (1/3 × 8)

B = 30 cm²

The side length a of the base is the square root of the base area, so a = √(30) = 5.5 cm.

Example 5

Height Calculation

Find the height of a square pyramid with a base side length of 4 cm and a volume of 32 cm³.

Solution

The volume V of a square pyramid is given by:

V = 1/3 × B × h,

so,

h = V / (1/3 × B)

Here, V = 32 cm³ and B = a² = 4² = 16 cm²

so

h = 32 / (1/3 × 16)

h = 6 cm

Example 6

Lateral Area Calculation

Calculate the lateral area of a square pyramid with a base side length of 5 cm and a slant height of 7 cm.

Solution

The lateral area L of a square pyramid is given by:

L = 1/2 × P × l

Here, P = 4a = 4 × 5 = 20 cm, and l = 7 cm,

so

L = 1/2 × 20 × 7

L = 70 cm²

Example 7

Base Diagonal Calculation

Calculate the length of the base diagonal of a right square pyramid with a base side length of 6 cm.

Solution

The base diagonal d of a square is given by:

d = a × √(2)

Here, a = 6 cm,

so,

d = 6 × √(2)

d = 8.5 cm

Example 8

Surface Area Calculation with Base Diagonal

Calculate the surface area of a right square pyramid with a base diagonal of 10 cm and a slant height of 8 cm.

Solution

First, calculate the base side length:

a = d / √(2)

a = 10 / √(2)

a = 7.1 cm

Then, calculate the base area:

B = a² = 7.1² = 50.4 cm²

The surface area A of a square pyramid is given by:

A = B + 1/2 × P × l

Here, P = 4a = 4 × 7.1 = 28.4 cm, and l = 8 cm,

so,

A = 50.4 + 1/2 × 28.4 × 8

A = 177 cm²

All images were created with GeoGebra.