JUMP TO TOPIC

In the intricate dance of geometric forms, the Octagon has assumed a position of quiet prominence. A figure with eight sides, it is neither as simple as a triangle nor as conventional as a square. Yet, it seamlessly blends simplicity with complexity, creating an equilibrium that has fascinated mathematicians, architects, and artists alike. Throughout history, the Octagon has symbolized harmony and balance, manifested in buildings from the 8th-century Umayyad architectural marvels to modern mixed martial arts cages.
This article embarks on a journey into the captivating world of octagons, their mathematical principles, their historical significance, and their role in our everyday lives. With each sentence, we will unravel another side of this enigmatic figure, delving deep into the multifaceted aspects of this eight-sided wonder. Buckle in and prepare to view your world from an eight-angled perspective.
Definition
A polygon having eight sides and eight angles is referred to as an octagon in geometry. The term originates from the Greek word “oktágōnon,” with “oktá” meaning eight and “gōnia” meaning angle.
There are various types of octagons, but the most common one is the regular Octagon, where all the sides and angles are equal. In a regular octagon, each interior angle measures 135 degrees, and the sum of all interior angles is 1080 degrees.
Octagons are widely used in architecture, design, and symbols due to their aesthetic appeal and geometric properties. An everyday example is the stop sign, which is shaped like a regular octagon. Below is the generic diagram of an octagon having eight sides.
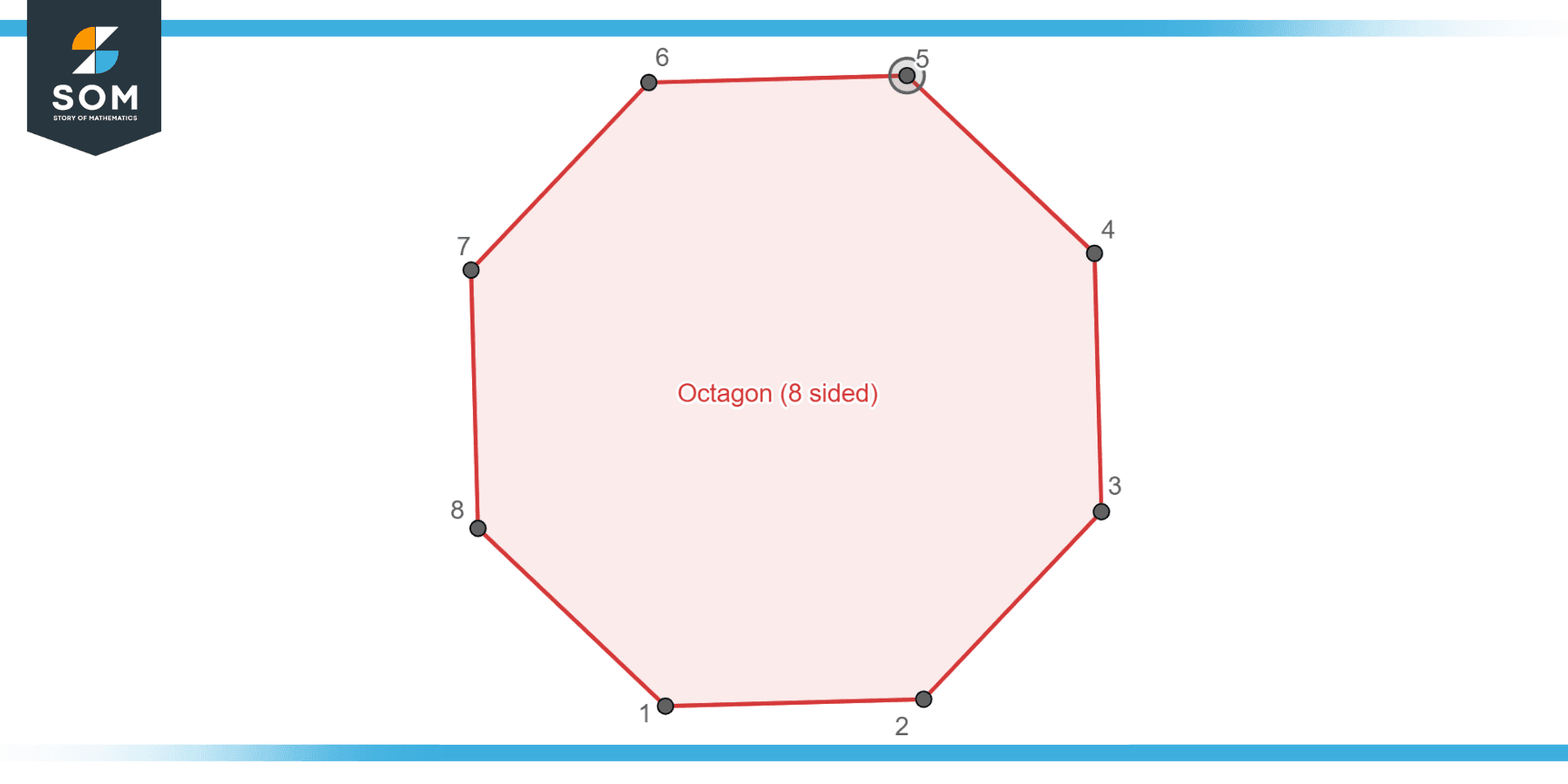
Figure-1: Generic octagon.
Historical Significance
The Octagon carries a significant historical and cultural weight in various societies around the world, dating as far back as ancient times. Let’s delve into some key instances that demonstrate the historical significance of the Octagon.
Ancient Architecture
Many ancient civilizations incorporated the Octagon into their architectural designs due to its unique geometric properties, blending the circular with the rectilinear. The octagonal Tower of the Winds in Athens was built in the second century BC. This structure considered the world’s first meteorological station, was adorned with sundials, a water clock, and a wind vane.
Baptistries in Christian Architecture
In Christian symbolism, the number eight often signifies rebirth and Resurrection, deriving from the tradition of celebrating the Resurrection on the eighth day (Sunday). Consequently, many early Christian and Byzantine baptisteries were built with an octagonal shape. Notably, the Lateran Baptistery in Rome, one of the oldest in the Christian world, follows this tradition.
Islamic Architecture
The Octagon plays a crucial role in Islamic architecture due to its geometric and symbolic significance. The Octagon often serves as a transitional shape between a square base and a circular dome in many mosques and Islamic buildings. A prominent example is the Dome of the Rock in Jerusalem, an octagonal building dating back to the 7th century AD, demonstrating the architectural transition from a square base to a circular dome.
Chinese Culture
In Chinese culture, the Octagon has significant importance in Feng Shui and I Ching. The Ba Gua, an octagonal diagram, is used in Feng Shui as a tool to understand how different aspects of life can be affected by a building or a room’s layout. Each of the eight sides corresponds to a different life aspect, such as wealth, family, or career.
Victorian Architecture
Due to the advocacy of phrenologist Orson Squire Fowler, who felt octagonal homes gave more sunlight and were simpler to heat and cool, octagons briefly gained favour in the United States in the middle of the 19th century. Though the octagon fad didn’t last long, it did result in some unique examples of Octagon houses that can still be seen today.
Octagon’s Geometry
An octagon, in its most general sense, is a polygon with eight edges (or sides) and eight vertices (or corners). While this term can refer to any eight-sided polygon without any qualifications, an “octagon” typically refers to a regular octagon – one with sides of equal length and internal angles of equal measure.
In a regular octagon, each side is of equal length, and every interior angle is equal to 135 degrees. To visualize this, consider a square and draw another square of the same size rotated by 45 degrees around the center point. The overlapping shape you create is a regular octagon. This shape is equilateral (all sides are equal in length) and equiangular (all internal angles are equal).
Any octagon’s inner angles add up to 1080 degrees, always, which is calculated by the formula (n-2) x 180, where n is the number of sides, which is 8 for an octagon. This formula holds true for any polygon, not just octagons.
A regular octagon can be split into eight congruent isosceles triangles. These triangles have a vertex angle of 135 degrees and two base angles, each of 22.5 degrees. Also, the regular Octagon can be divided into one square and eight right triangles, offering various possibilities for geometric problem-solving.
The Octagon also plays a significant role in the field of tessellation, which is defined as a group of closely spaced-out forms, particularly polygons in a repetitive pattern without gaps or overlapping. The regular Octagon is not tessellated on its own, but it can form a tessellation when combined with squares or other shapes.
Octagon Types
An octagon, by definition, is a polygon that has eight sides. However, octagons can vary widely in their shapes and properties based on the lengths of their sides and the magnitudes of their angles. Here are some common types of octagons.
Regular Octagon
This is the most symmetrical type of Octagon, where all sides and all angles are equal. Each interior angle in a regular octagon measures 135 degrees, and every side is the same length. Below is the generic diagram of a regular octagon having eight sides.
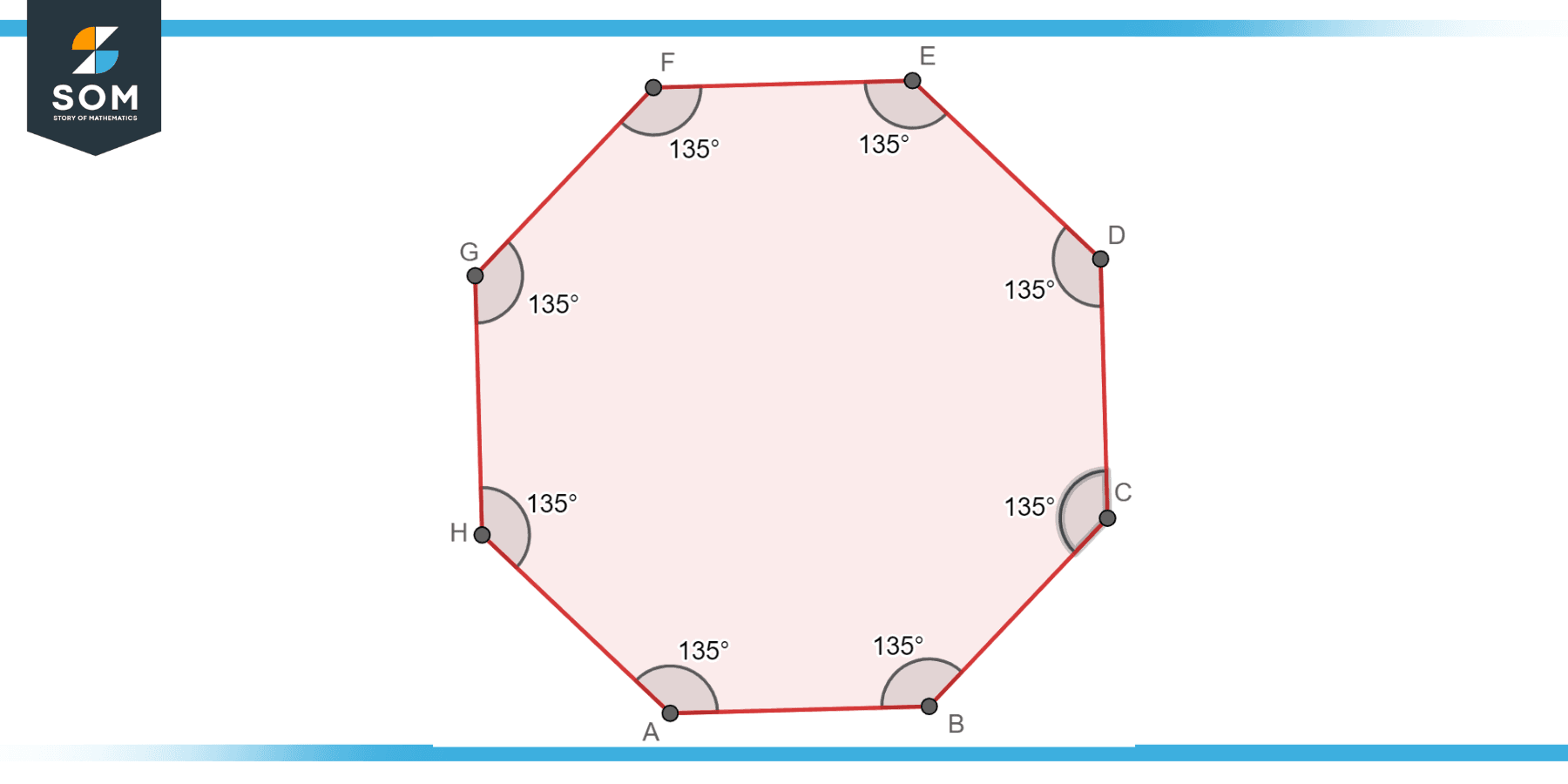
Figure-2: Regular octagon.
Irregular Octagon
This is an octagon where not all sides and angles are equal. An irregular octagon can still be concave or convex, but it doesn’t have the same level of symmetry as a regular octagon. Below is the generic diagram of an irregular octagon having eight sides.
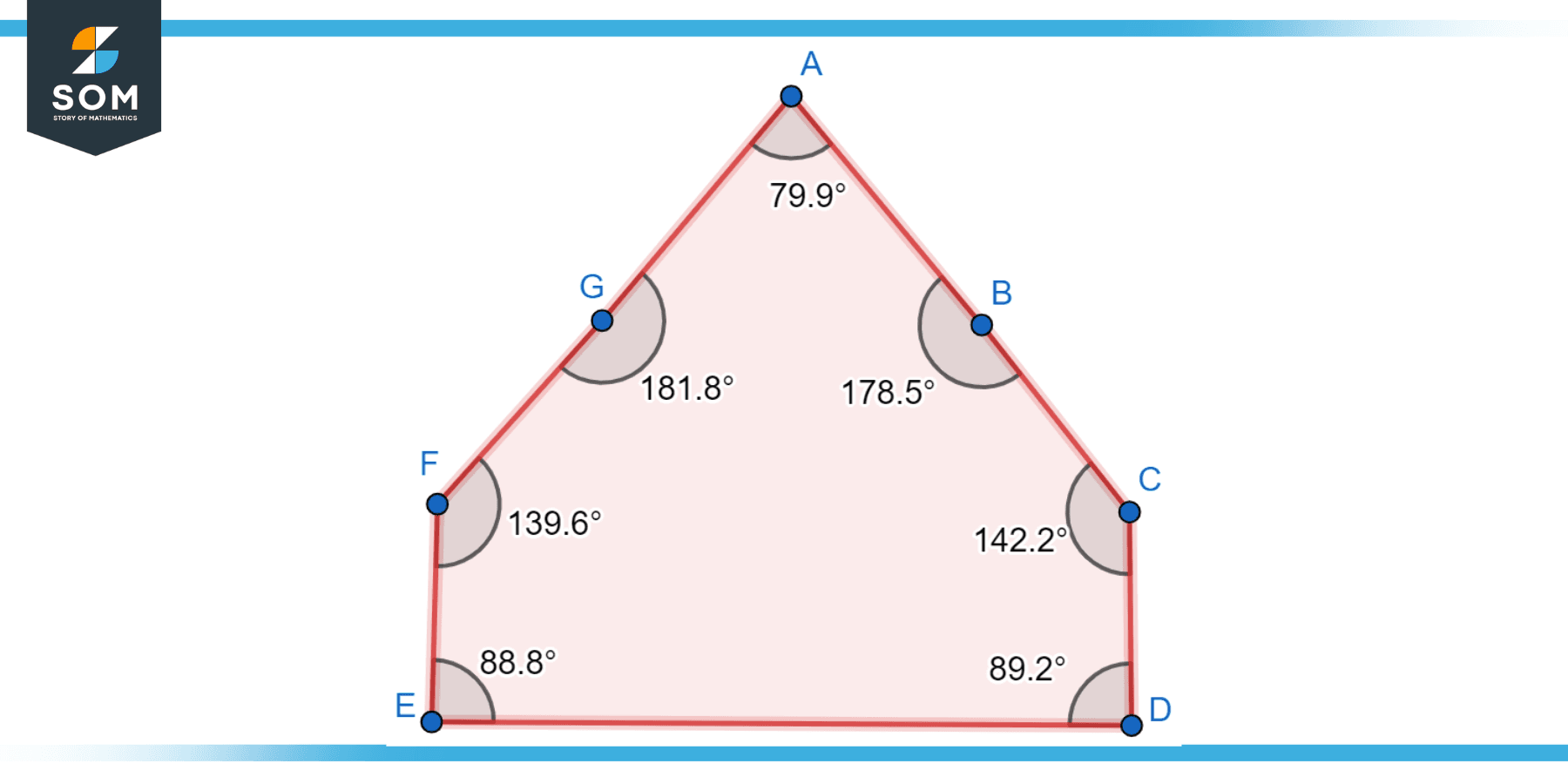
Figure-3: Irregular octagon.
Concave Octagon
A concave octagon has at least one angle that is more than 180 degrees, giving the shape a “caved-in” appearance. This is in contrast to a convex octagon, where all angles are less than 180 degrees. Below is the generic diagram of a concave octagon having eight sides.
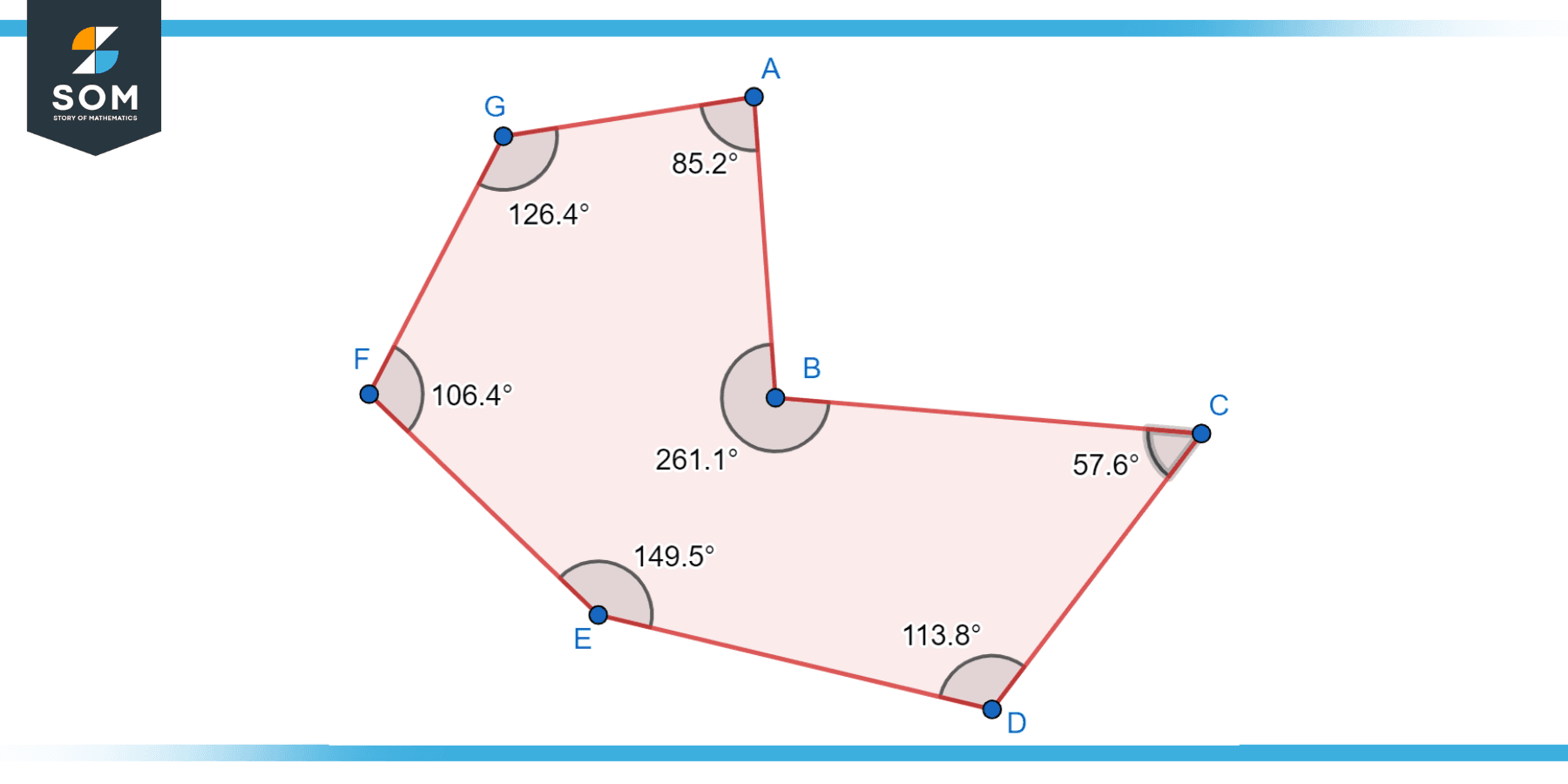
Figure-4: Concave octagon.
Convex Octagon
A convex octagon has all its interior angles less than 180 degrees. Accordingly, no line segment connecting any two points along the boundary ever leaves the polygon. Both regular and irregular octagons can be convex. Below is the generic diagram of a convex octagon having eight sides.
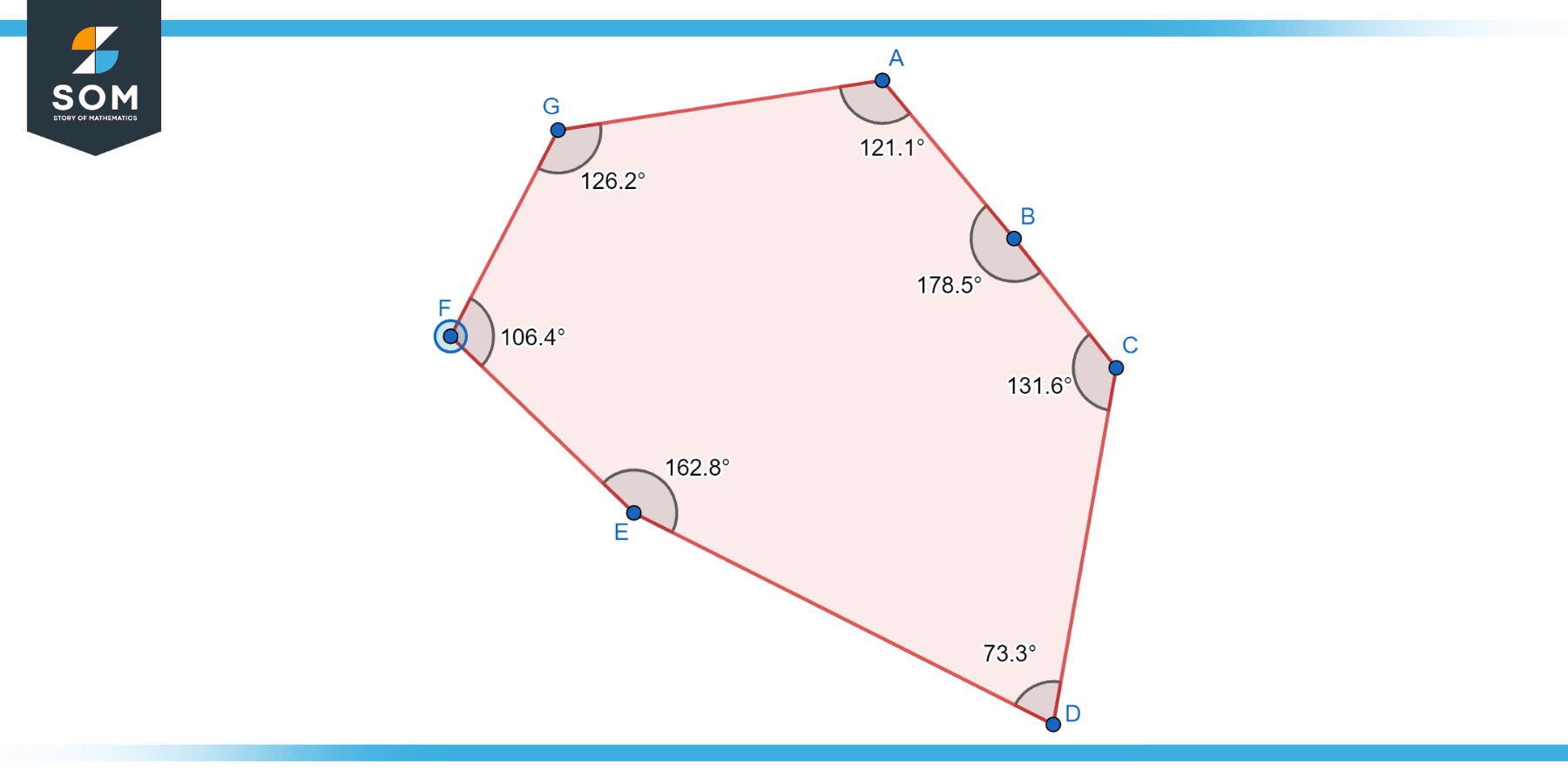
Figure-5: Convex octagon.
Related Parameters
In geometric mathematics, there are several formulas associated with octagons, especially regular octagons. The following is a list of some of the more noteworthy ones.
A Regular Octagon’s Perimeter
The following formula can be used to get a regular octagon’s perimeter (P) with equal-length sides.
P = 8 × s
where s is the length of one side.
Area of a Regular Octagon
The area (A) of a regular octagon can be calculated using the formula;
$$A = 2 \times s^2 (1+\sqrt{2})$$
where s is the length of one side.
Internal Angles of an Octagon
The formula for the sum of any polygon’s internal angles is;
Sum = (n-2) × 180°
Where n is the number of sides, for an octagon, n is 8, so the sum of the interior angles is 1080°. For a regular octagon, each individual angle is 135°.
Exterior Angles of a Regular Octagon
Any polygon’s outer angles add up to 360°. For a regular octagon, each individual exterior angle would be 360°/8 = 45°.
Diagonals of an Octagon
The number of diagonals (D) in an octagon can be calculated using the formula;
D = n × (n-3)/2
where n is the number of sides. For an octagon, n is 8, so the number of diagonals is 20.
Apothem of a Regular Octagon
The apothem (a) of a regular octagon (which is the distance from the center to any side, perpendicular to that side) can be calculated from the side length (s) using the formula;
a = s/(2 × tan(π/8))
Octagon Applications
Certainly, octagons are found in a variety of real-world applications, many of which may not even be apparent at first glance. The Octagon is particularly notable in traffic regulations, sports, architecture, and design due to its easily recognizable shape and its properties of balance and symmetry. Here’s a more detailed look.
Traffic Regulations
Perhaps the most common use of an octagon in everyday life is the stop sign. In many countries, traffic stop signs are made in the shape of a regular octagon. The purpose of this eight-sided figure in traffic regulation is primarily psychological and practical. The unique shape is easily recognizable and stands out among other road signs, allowing drivers to identify it quickly, even at a distance or in low visibility conditions. This prompt recognition is crucial in ensuring the safety and smooth flow of traffic.
Sports
In the sport of Mixed Martial Arts (MMA), contests are often held in an eight-sided cage known as “The Octagon.” This design choice isn’t merely aesthetic; it serves a practical purpose. The Octagon provides more space than a traditional boxing ring, allowing athletes to maneuver more freely. Its shape also means there are no corners where a competitor could be trapped. Moreover, the octagonal design provides better sightlines for spectators and officials, ensuring fair and enjoyable viewing.
Architecture
The Octagon is frequently found in architecture, both in the structural design of buildings and in decorative elements. The shape is often used because it combines the strength and stability of squares or rectangles with the aesthetic appeal of circles. For example, the octagonal floor plan has been used in high-profile buildings like the Palazzo Reale in Naples or the Leaning Tower of Pisa. Additionally, the Octagon is commonly used in the design of less grand structures like gazebos, where it provides a pleasing, symmetrical shape and broad views of the surrounding area.
Interior Design
Octagonal shapes are often used in tiles, carpets, and other interior design elements. Using octagonal tiles can create interesting and intricate patterns that square or rectangular tiles can’t. Octagonal mirrors or wall decorations can also provide a distinctive alternative to the usual rectangular or circular options.
Urban Planning
In city planning, octagonal buildings and structures can create efficient, aesthetically pleasing layouts. For example, the Octagon on Roosevelt Island in New York was originally designed as a hospital. Its unique shape allowed for maximum light and air circulation. Today, it has been converted into a residential building, but its octagonal design is still a defining feature.
Symbolism and Spiritual Practices
In various cultures and spiritual practices, the Octagon holds significant symbolic meaning. In Christianity, the Octagon is often associated with regeneration, rebirth, and transition from earthly to heavenly. Many baptismal fonts in early Christian churches were octagonal for this reason. In Chinese culture, the Ba Gua, an octagonal diagram, is used in Feng Shui to evaluate energy flow and balance in a space.
Coding and Computers
In computer graphics, octagonal shapes are sometimes used as approximations of circles, as the eight-sided shape can be simpler to generate and manipulate programmatically. In the context of digital images, the Octagon can be used as the basis for certain algorithms for blurring or for detecting edges and shapes within an image.
Table Games
Octagons are also found in various board games and table games. For example, in the Settlers of Catan game, hexagonal tiles are surrounded by octagonal “ports.” Octagonal gaming tables are also popular for poker and other card games, providing equitable seating positions for numerous players.
Exercise
Example 1
If the side length of a regular octagon is 5 cm, what is the perimeter?
Solution
The perimeter (P) of a regular octagon is given by the formula P = 8×s, where s is the length of a side.
P = 8 × 5 = 40 cm.
So, the perimeter of the Octagon is 40 cm.
Example 2
What is the area of the octagon given in Figure-6?
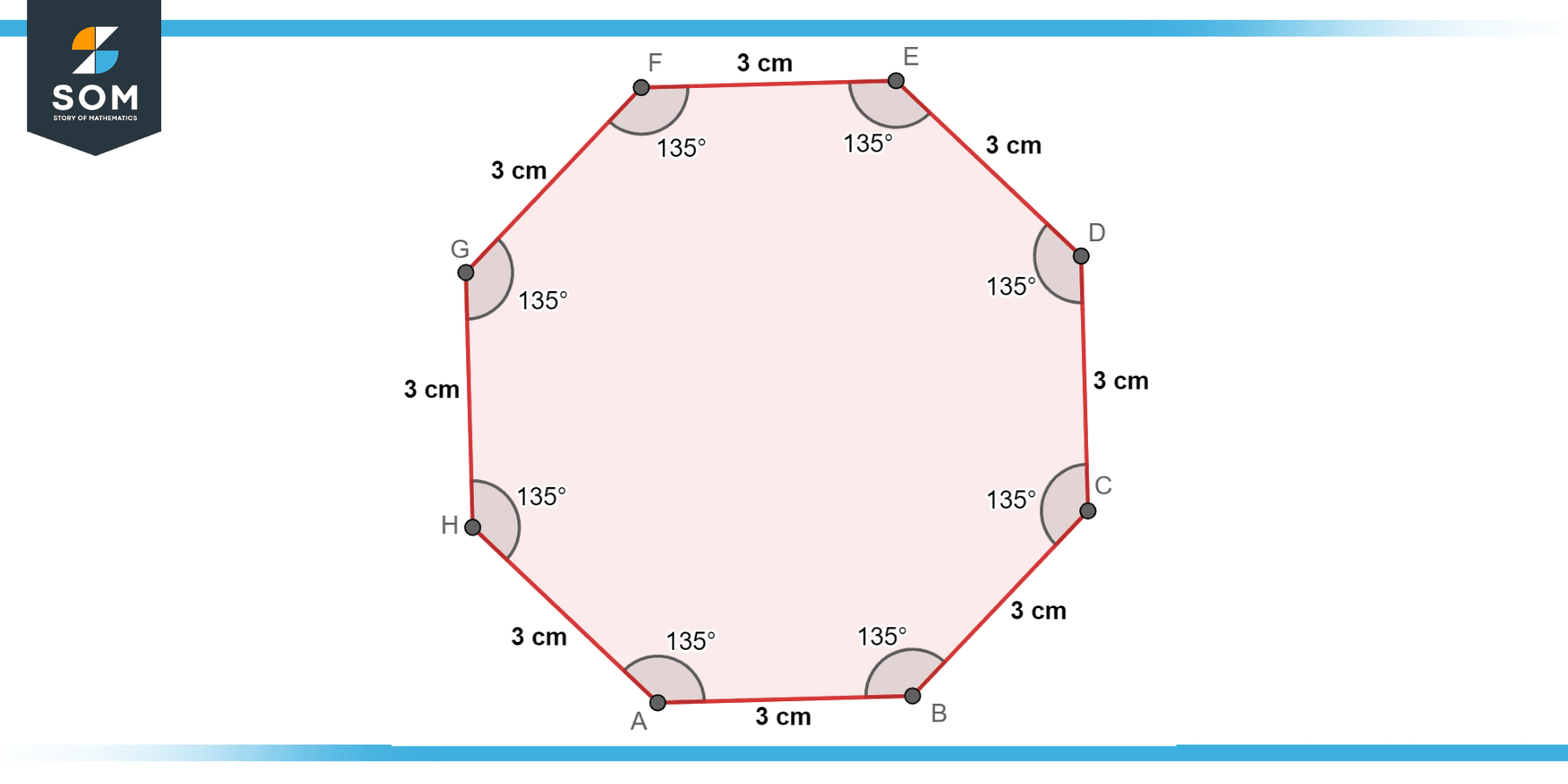
Figure-6.
Solution
The formula for the area (A) of a regular octagon is $A = 2 \times s^2 (1+\sqrt{2})$, where s is the length of a side.
$$A = 2 \times 3^2 (1+\sqrt{2})$$
$$A = 2 \times 9 (1+\sqrt{2})$$
$$A = 18(1+\sqrt{2})$$
$$A = 18+18\sqrt{2}$$
So, the area of the Octagon is $A = 18(1+\sqrt{2})$ cm².
Example 3
How many interior angles are there in a standard octagon, and what are their measurements?
Solution
An octagon’s internal angles add up to 1080 degrees. Since a regular octagon has equal angles, each angle measures 1080° / 8 = 135°.
So, each interior angle of a regular octagon is 135°.
Example 4
How many outside (exterior) angles are there in a normal octagon, and what are their measurements?
Solution
Solution: The sum of the exterior angles for any polygon is 360°. For a regular octagon, each individual exterior angle would be 360° / 8 = 45°.
So, each exterior angle of a regular octagon is 45°.
Example 5
How many diagonals does an octagon have?
Solution
The number of diagonals (D) in a polygon is given by the formula D = n(n-3)/2, where n is the number of sides. For an octagon, n is 8.
D = 8 × (8 – 3)/2
D = 8 × 5/2
D = 20
So, an octagon has 20 diagonals.
Example 6
Apothem of a Regular Octagon: If the side length of a regular octagon is 4 cm, what is the length of the apothem?
Solution
The formula for the apothem (a) of a regular octagon is;
a = s/(2 × tan(π/8)),
where s is the side length. By putting the value of s, we get
a = 4/(2 × tan(π/8))
a = 4/(2 × 0.414)
a = 4.83 cm (approximately)
So, the apothem of the Octagon is approximately 4.83 cm.
Example 7
If the area of a regular octagon is 48 cm², what is the length of one side?
Solution
Using the formula for the area of an octagon $A = 2 \times s^2 (1+\sqrt{2})$, we solve for s.
$$48 = 2 \times s^2 (1+\sqrt{2})$$
Dividing both sides by 2(1 + √2) gives us
$$s^2 = \frac{48}{2 \times (1+\sqrt{2})}$$
Taking the square root of both sides gives us
$$s = \sqrt{\frac{48}{2 \times (1+\sqrt{2})}}$$
s = 2.41 cm (approximately)
So, the side length of the Octagon is approximately 2.41 cm.
Example 8
If the side length of a regular octagon is 2 cm, What is the circumradius (the circumscribed circle’s radius)?
Solution
The formula for the circumradius R is R = s/(2×sin(π/n)), where n is the number of sides and s is the side length.
R = 2 / (2 × sin(π/8))
R = 2 / (2 × 0.383)
R = 2.61 cm (approximately)
So, the circumradius of the Octagon is approximately 2.61 cm.
All images were created with GeoGebra.
