JUMP TO TOPIC

Trapezoids are captivating geometric shapes with a unique blend of symmetry and versatility. Defined as a quadrilateral with one pair of parallel sides, trapezoids play a significant role in the world of geometry, offering a wealth of mathematical properties and applications. From architectural structures to artistic designs, trapezoids are omnipresent, showcasing their intriguing attributes and contributing to various fields.
In this article, we will embark on a journey to unravel the mysteries of trapezoids, exploring their defining characteristics, diverse types, and captivating mathematical concepts. Join us as we delve into the enchanting realm of trapezoids, discovering their hidden wonders and appreciating their significance in geometric shapes.
Definition
A trapezoid is a quadrilateral with one pair of parallel sides. This unique geometric shape showcases a combination of straight lines and distinct angles, making it a fascinating subject of study in the field of geometry. In a trapezoid, the non-parallel sides are called legs, while the parallel sides are called bases. Unlike other quadrilaterals, trapezoids do not possess equal angles or sides, allowing for a wide range of possible configurations. The symmetry and distinct properties of trapezoids contribute to their prominence in mathematics, engineering, and architectural design. Through their versatility and intriguing geometric properties, trapezoids continue to captivate the minds of scholars and enthusiasts alike. Below we present the generic diagram of the trapezoid.
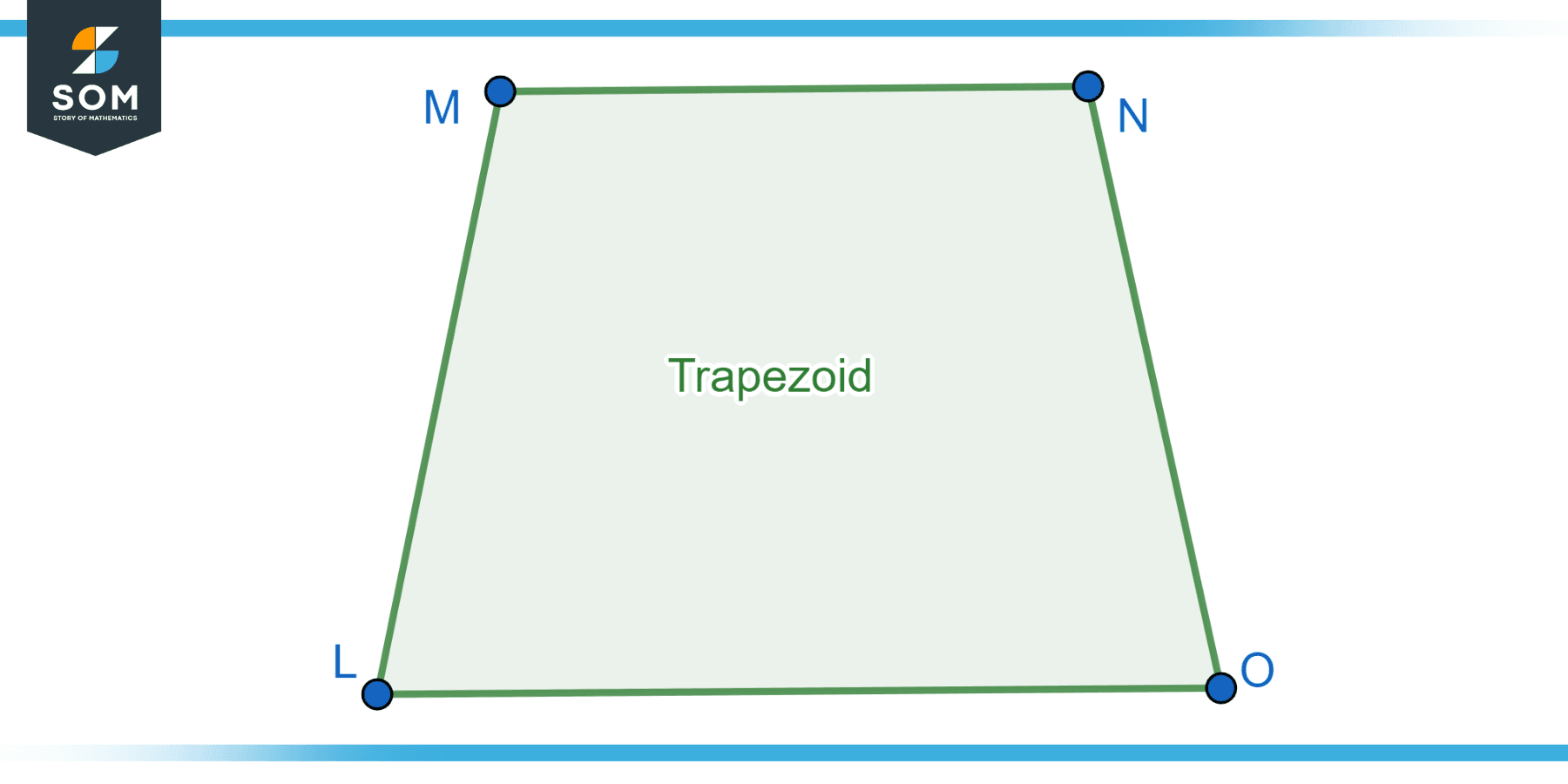
Figure-1: Generic trapezoid.
Historical Significance
The trapezoid has a rich historical background that dates back to ancient civilizations and the development of mathematical knowledge. The study of geometry and geometric shapes played a fundamental role in the intellectual pursuits of ancient Greek mathematicians, notably Euclid, who laid the foundations of geometric principles in his work “Elements.”
The concept of the trapezoid was integral to the ancient Greeks’ exploration of quadrilaterals and their properties. Euclid defined the trapezoid as a quadrilateral with one pair of parallel sides. His seminal work provided a systematic approach to understanding and classifying geometric shapes, including the trapezoid, within a broader geometric framework.
Over the centuries, the study of trapezoids continued to evolve, with scholars and mathematicians exploring their properties and relationships with other shapes. In the Islamic Golden Age, scholars like Al-Khwarizmi further expanded geometric knowledge, contributing to the development of algebraic methods to solve problems involving trapezoids and other polygons.
During the Renaissance, the works of renowned mathematicians such as Descartes and Pascal brought new insights into the realm of geometry. Their advancements in coordinate systems and projective geometry led to a deeper understanding of trapezoids and their properties.
Today, the study of trapezoids and their applications extends beyond mathematics, finding relevance in diverse fields such as architecture, engineering, physics, and computer graphics. The historical journey of the trapezoid stands as a testament to humanity’s continuous exploration and fascination with geometric shapes, leaving a lasting impact on mathematical education and practical applications.
Types
Specific characteristics and properties define several main types of trapezoids. Let’s explore them:
Isosceles Trapezoid
An isosceles trapezoid is a trapezoid in which the legs (non-parallel sides) have the same length. This means that both base angles are congruent. The bases of an isosceles trapezoid are still parallel, but the legs are of equal length. Below we present the generic diagram of the isosceles trapezoid.
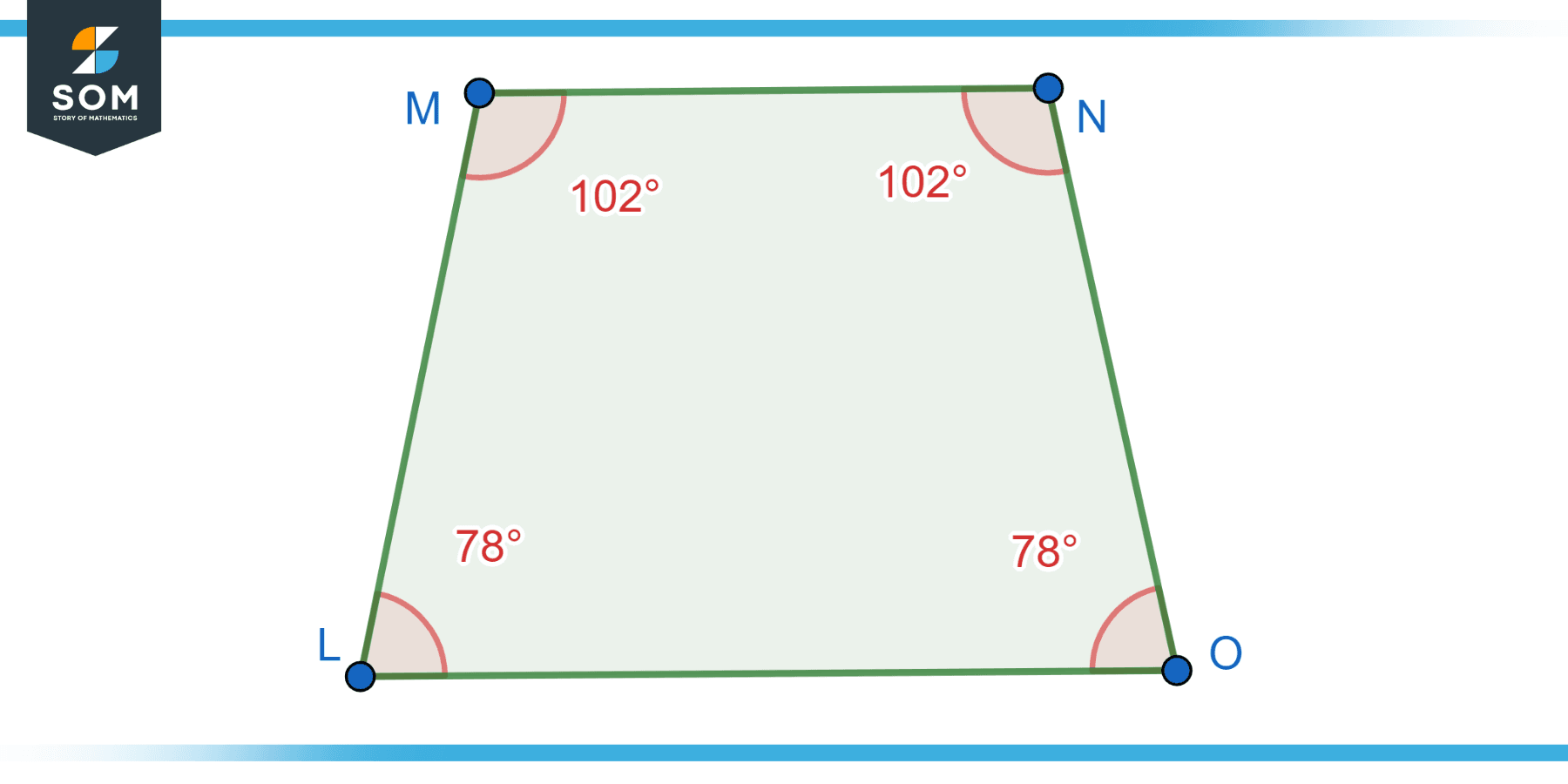
Figure-2: Isosceles trapezoid.
Right Trapezoid
A right trapezoid is a trapezoid that has one right angle. This means that one of the base angles measures 90 degrees, while the opposite base angle is its supplementary angle (measuring 90 degrees as well). Below we present the generic diagram of the right trapezoid.
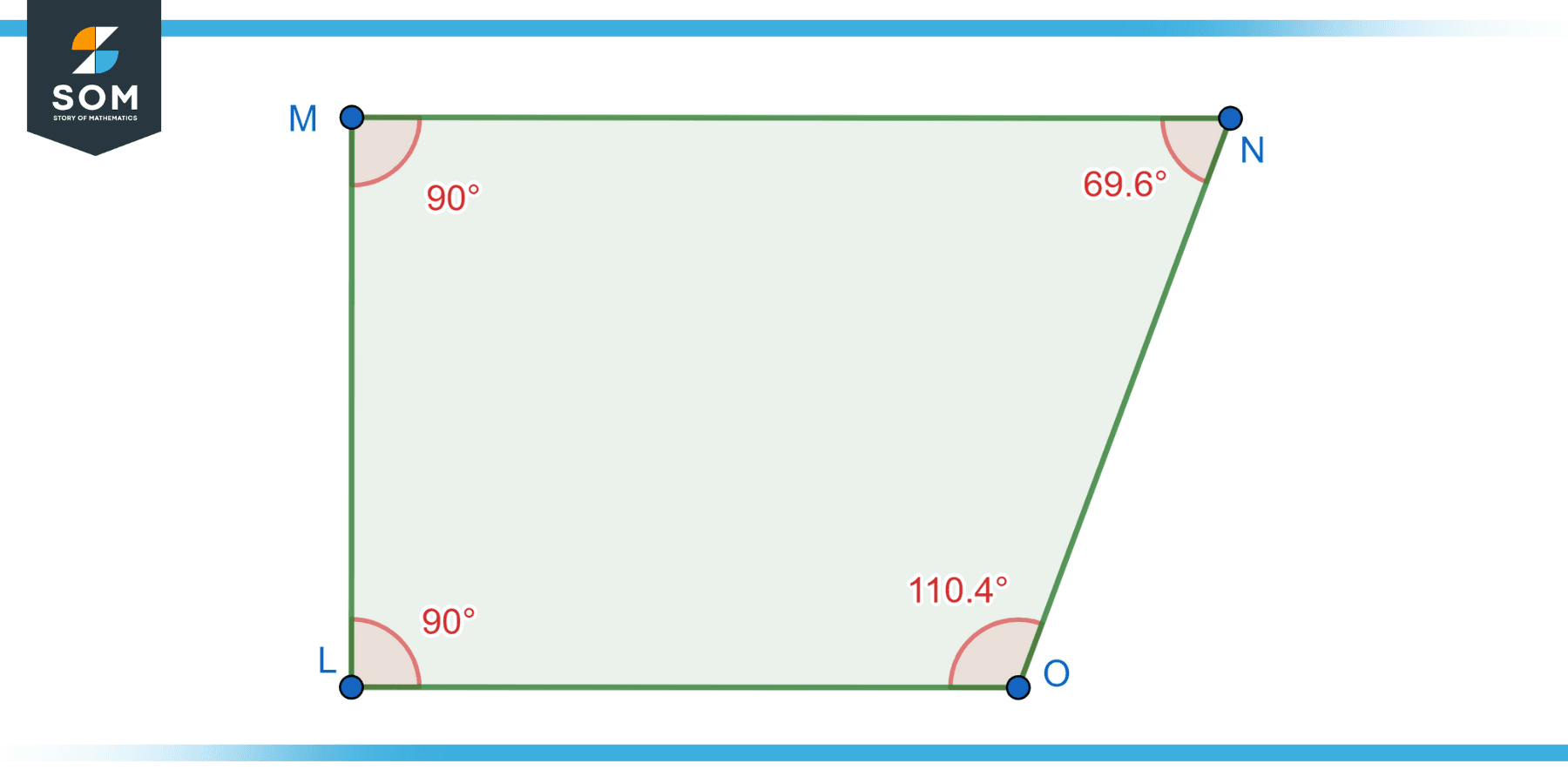
Figure-3: Right trapezoid.
Scalene Trapezoid
A scalene trapezoid is a trapezoid in which none of the sides or angles are equal. It has no congruent sides or angles, making it the most general type of trapezoid. Below we present the generic diagram of the scalene trapezoid.
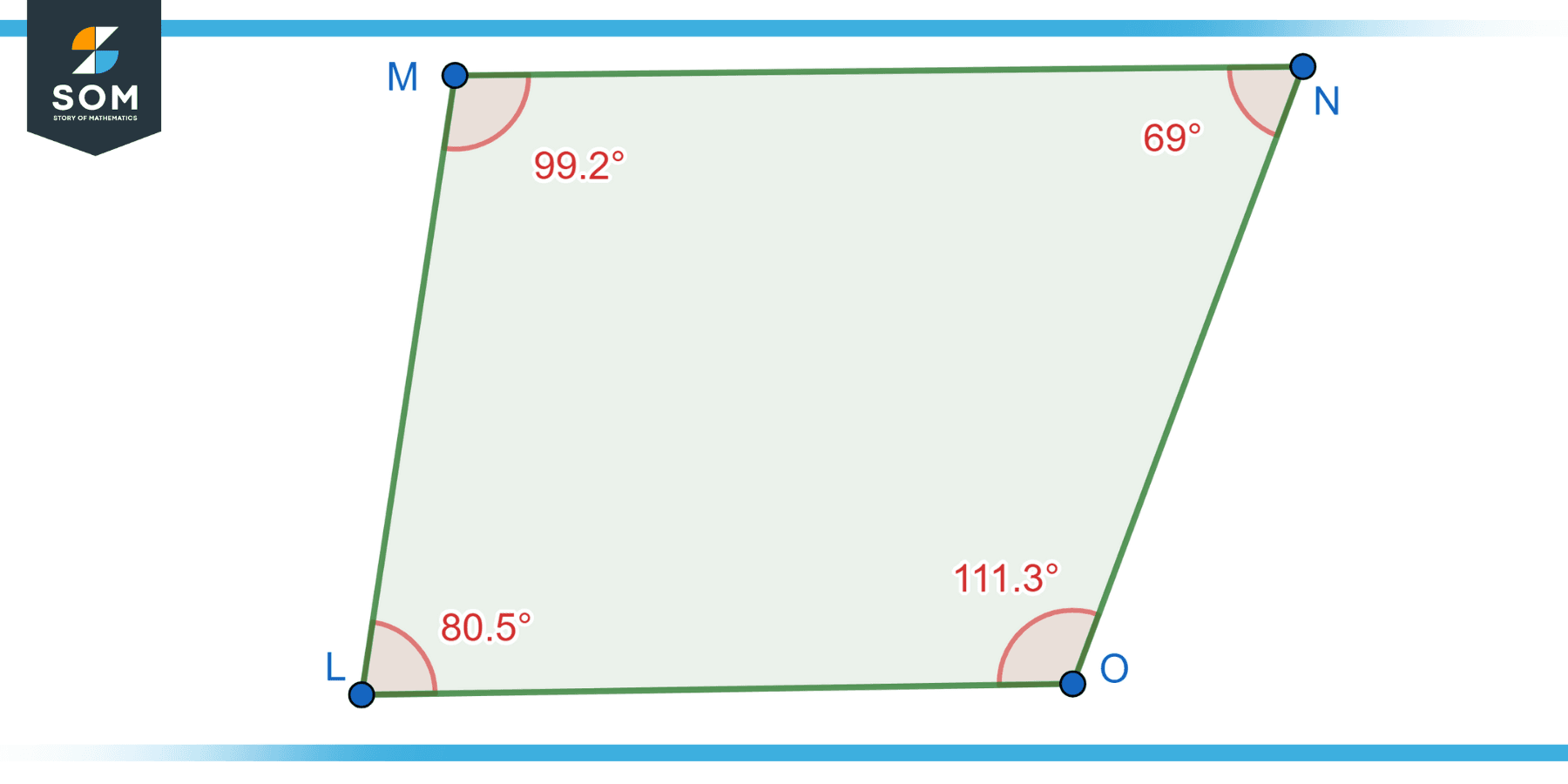
Figure-4: Scalene trapezoid.
Rectangle
Although a rectangle is not typically referred to as a trapezoid in general geometry, it can be seen as a special case of a trapezoid. A rectangle can be considered a trapezoid with two pairs of parallel sides and congruent base angles. Below we present the generic diagram of the rectangle trapezoid.

Figure-5: Rectangle trapezoid.
These types of trapezoids exhibit varying properties and relationships between their sides, angles, and bases. Understanding these distinctions can aid in solving geometric problems and analyzing the characteristics of specific trapezoids.
Properties
A trapezoid is a geometric shape with several distinct properties:
Four Sides
A trapezoid is a quadrilateral with four sides. It is characterized by having two sides that are parallel to each other and two sides that are not parallel.
Parallel Bases
The bases of a trapezium are its parallel sides. These bases are parallel to each other and are the longest sides of the trapezoid.
Legs
The legs of a trapezium are its remaining two sides. They connect the non-parallel sides and are typically shorter in length than the bases.
Base Angles
The angles formed between the bases and the legs are known as the base angles. Each base angle is adjacent to one of the bases.
Opposite Angles
The angles formed between the legs of the trapezoid are called the opposite angles. Each opposite angle is across from another opposite angle.
The sum of Base Angles
The sum of the base angles in a trapezoid is always equal to 180 degrees. This property holds true for all trapezoids.
Diagonals
The trapezoid has two diagonals, which are line segments connecting the non-adjacent vertices. These diagonals are not necessarily equal in length.
Midsegment
A line segment connecting the midpoints of the two non-parallel sides is known as the midsegment of a trapezium. It is parallel to the bases and is equal in length to the average of the bases.
Area
The following formula can be used to determine a trapezoid’s area: A = ((base1 + base2) × height) / 2, where A represents the area and height refers to the perpendicular distance between the bases.
Symmetry
Trapezoids are generally not symmetric, as their sides and angles can have different lengths and measures. However, certain special trapezoids, such as isosceles trapezoids, possess symmetry properties.
Understanding these properties helps in identifying and analyzing trapezoids in various mathematical problems and real-world situations.
Ralevent Formulas
Certainly! Here are the related formulas associated with a trapezoid:
Area (A)
The following formula can be used to determine a trapezoid’s area: A = ((base1 + base2) × height) / 2, where base1 and base2 represent the lengths of the two parallel bases, and height refers to the perpendicular distance between the bases. The bases are the longer sides of the trapezoid.
Perimeter (P)
The perimeter of a trapezoid is calculated by adding the lengths of all four sides. Since the trapezoid has two parallel sides (bases) and two non-parallel sides (legs), the perimeter can be expressed as: P = base1 + base2 + leg1 + leg2.
Midsegment Length (m)
A line segment that joins the midpoints of the two non-parallel sides is known as the midsegment of a trapezium. It is parallel to the bases and equal in length to the average of the two bases. The formula to find the midsegment length is: m = (base1 + base2) / 2.
Diagonal Length (d)
A trapezoid has two diagonals, which are line segments connecting non-adjacent vertices. The formula to find the length of a diagonal depends on the given information. If the diagonals and the angle between them are known, the formula is derived from the Law of Cosines: d = √(side₁² + side₂² – 2 × side₁ × side₂ × cos(θ)). If the lengths of the bases and the height are known, the formula for the diagonal length can be derived using the Pythagorean theorem.
These formulas provide a comprehensive understanding of the properties and measurements associated with a trapezoid. They enable the calculation of important quantities such as area, perimeter, midsegment length, and diagonal length, aiding in various mathematical and practical applications involving trapezoids.
Applications
The trapezoid, with its unique properties and distinctive shape, finds practical applications across various fields, showcasing its versatility and significance. Let’s delve into some notable applications of trapezoids in different domains.
Architecture and Construction
Trapezoids are frequently employed in architectural designs, particularly in the construction of roofs. The shape of a trapezoid allows for efficient water drainage and provides stability, making it ideal for creating sloping or gabled roofs.
Engineering and Structural Design
Trapezoids play a vital role in engineering and structural design, especially in the construction of bridges and trusses. The stability and load-bearing capacity of trapezoidal structures make them suitable for supporting heavy loads and distributing forces effectively.
Finance and Economics
Trapezoidal rule is utilized in financial calculations, such as estimating the area under a curve for numerical integration. It helps approximate the values of definite integrals, enabling the evaluation of financial quantities, such as option pricing or portfolio risk measures.
Mathematics and Geometry Education
Trapezoids serve as important subjects of study in mathematics and geometry education. They help students understand fundamental geometric concepts such as parallel lines, angles, and quadrilaterals. Trapezoids also provide a practical context for learning about properties like bases, legs, and diagonals.
Graphics and Computer Modeling
Trapezoids are utilized in computer graphics and modeling, particularly for rendering two-dimensional shapes and creating visual effects. They form the basis for various algorithms and techniques used in computer-aided design (CAD), animation, and video game development.
Physics and Mechanics
Trapezoidal configurations are often encountered in mechanical systems, such as pulley arrangements, where trapezoidal belts or chains are employed for power transmission. The geometry of the trapezoid ensures smooth and efficient transfer of rotational motion.
Surveying and Land Measurement
Trapezoids find applications in land surveying and measurement, especially in irregular-shaped plots or fields. By dividing the area into trapezoids, surveyors can calculate the total land area accurately using geometric formulas.
Art and Design
Trapezoids inspire artistic expression and are incorporated into various design elements. In graphic design, trapezoidal shapes can create dynamic and visually appealing compositions, adding a sense of movement and balance to artworks.
Industrial Manufacturing
Trapezoidal profiles are commonly used in industrial manufacturing processes, such as conveyor belts and timing belts. The shape ensures a secure grip and efficient transfer of motion in machinery and production lines.
Pattern Making and Sewing
Trapezoidal patterns are commonly used in garment and fabric design. They serve as the basis for creating various clothing components, such as sleeves, skirts, and pants. Trapezoidal panels allow for shaping and fitting garments to different body contours.
These are just a few examples highlighting the diverse applications of trapezoids across different fields. Their geometry and unique characteristics make them valuable in practical contexts, demonstrating the enduring relevance of this geometric shape. Understanding the applications of trapezoids in these diverse fields highlights their significance and utility. From architecture and mathematics education to computer graphics and manufacturing, the properties of trapezoids find practical implementation across a range of disciplines, contributing to innovation and problem-solving.
Exercise
Example 1
In a trapezoid, the lengths of the bases are 10 centimeters and 6 centimeters, and the height is 8 centimeters. What is the area of the trapezoid?
Solution
Given: Base1 = 10 centimeters, Base2 = 6 centimeters, Height = 8 centimeters.
The area of a trapezoid is calculated using the formula
A = ((base1 + base2) × height) / 2.
Substituting the given values, we have:
A = ((10 centimeters + 6 centimeters) × 8 centimeters) / 2
A = 56 square centimeters.
Therefore, the area of the trapezoid is 56 square centimeters.
Example 2
In a trapezoid, the lengths of the bases are 12 meters and 8 meters, and the length of one leg is 5 meters. Find the length of the other leg.
Solution
Given: Base1 = 12 meters, Base2 = 8 meters, Leg1 = 5 meters.
To find the length of the other leg, we can use the formula for the midsegment of a trapezoid, which is:
m = (base1 + base2) / 2
Substituting the given values, we have:
m = (12 meters + 8 meters) / 2
m = 10 meters
Therefore, the length of the other leg is 10 meters.
Example 3
In a trapezoid, the lengths of the bases are 16 inches and 10 inches, and the length of one leg is 6 inches. Find the length of the other leg.
Solution
Given: Base1 = 16 inches, Base2 = 10 inches, Leg1 = 6 inches.
To find the length of the other leg, we can use the formula for the midsegment of a trapezoid, which is:
m = (base1 + base2) / 2.
Substituting the given values, we have:
m = (16 inches + 10 inches) / 2
m = 13 inches
Therefore, the length of the other leg is 13 inches.
Example 4
In a trapezoid given in Figure-6, find the length of the other diagonal.
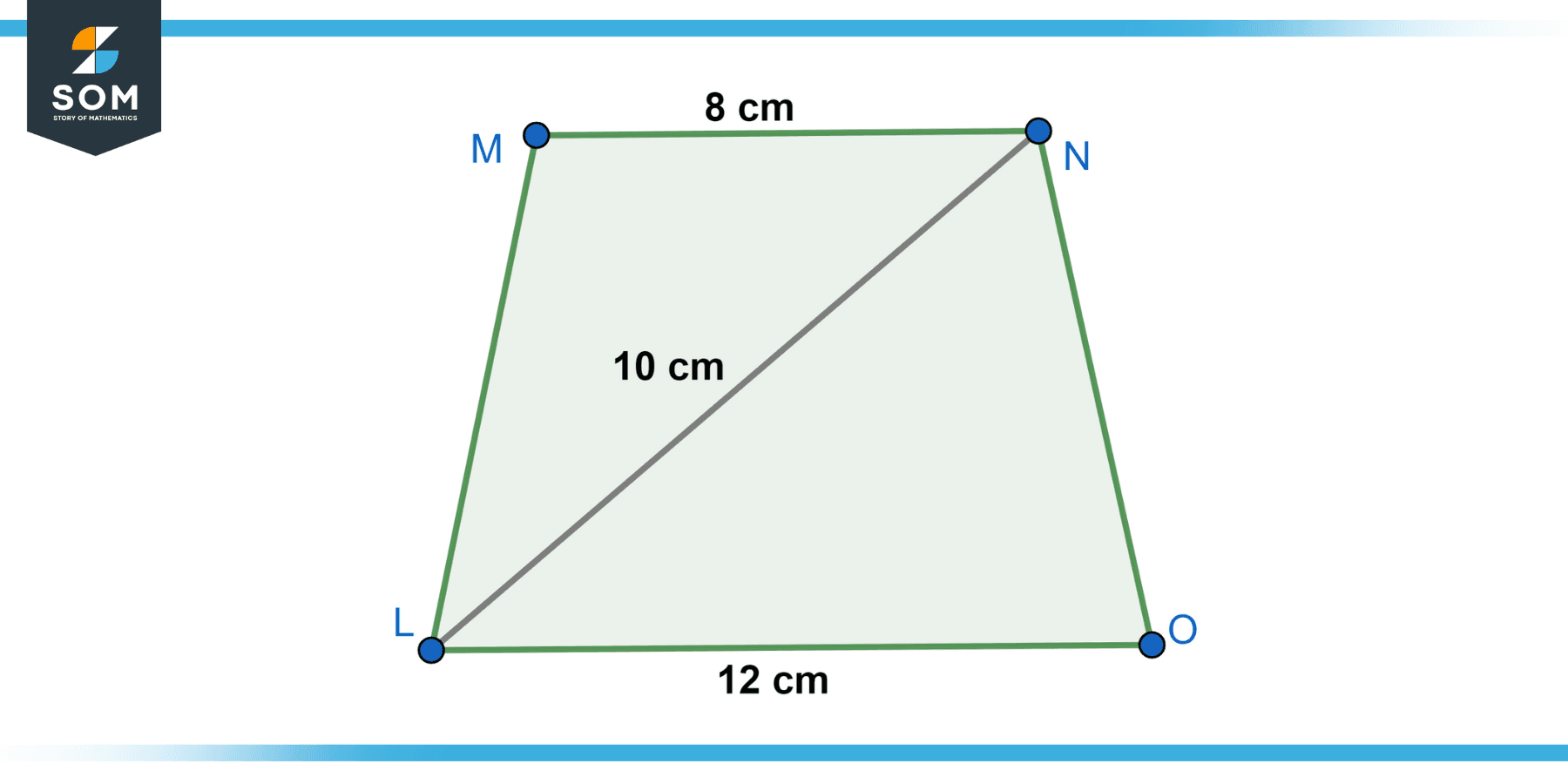
Figure-6.
Solution
Given: Base1 = 8 centimeters, Base2 = 12 centimeters, Diagonal1 = 10 centimeters.
To find the length of the other diagonal, we can use the formula derived from the Law of Cosines:
d = √(side₁² + side₂² – 2 × side₁ × side₂ × cos(θ))
In this case, the lengths of the bases are known, so the formula becomes:
d = √((8²) + (12²) – 2 × 8 × 12 × cos(θ))
To find the length of the other diagonal, the angle value is required.
Example 5
In a trapezoid, the lengths of the bases are 15 inches and 9 inches, and the length of one diagonal is 12 inches. Find the length of the other diagonal.
Solution
Given: Base1 = 15 inches, Base2 = 9 inches, Diagonal1 = 12 inches.
To find the length of the other diagonal, we can use the formula derived from the Law of Cosines:
d = √(side₁² + side₂² – 2 × side₁ × side₂ × cos(θ))
In this case, the lengths of the bases are known, so the formula becomes:
d = √((15 inches)² + (9 inches)² – 2 × 15 inches × 9 inches × cos(θ))
To find the length of the other diagonal, the angle value is required.
Example 6
In a trapezoid, the lengths of the bases are 14 centimeters and 10 centimeters, and the length of one diagonal is 8 centimeters. Find the measure of the included angle.
Solution
Given: Base1 = 14 centimeters, Base2 = 10 centimeters, Diagonal1 = 8 centimeters.
To find the measure of the included angle, we can use the formula derived from the Law of Cosines:
angle = acos((diagonal₁² + diagonal₂² – side₁² – side₂²) / (2 × diagonal₁ × diagonal₂))
In this case, we only have the length of one diagonal, so we need additional information or the value of the second diagonal to find the measure of the included angle.
Example 7
In a trapezoid, the lengths of the bases are 18 meters and 12 meters, and the measure of one base angle is 60 degrees. Find the measure of the other base angle.
Solution
Given: Base1 = 18 meters, Base2 = 12 meters, Angle1 = 60 degrees.
Since a trapezoid has two pairs of opposite angles, the other base angle can be measured by subtracting the given angle from 180 degrees. Therefore, the measure of the other base angle is 180 degrees – 60 degrees = 120 degrees.
Example 8
In a trapezoid, the lengths of the bases are 7 inches and 9 inches, and the measure of one base angle is 45 degrees. Find the measure of the other base angle.
Solution
Given: Base1 = 7 inches, Base2 = 9 inches, Angle1 = 45 degrees.
Since a trapezoid has two pairs of opposite angles, the measure of the other base angle is also 45 degrees. Therefore, the measure of the other base angle is 45 degrees.
All images were created with GeoGebra.
