How To Find 16 Square Root: Detailed Explanation

The square root of $16$ is $4$.

The square root of $16$ can be written as $\sqrt{16}$, as we know the square root symbol is $\sqrt{}$ and the answer of $\sqrt{16}$ is $4$. Solving the square root of any number is quite easy, and all you need to do is have a basic concept of the term factor.

In mathematics, it is important to divide the big number in to smaller ones before solving for square root, and this is also the case with the number $16$. The number $16$ can be written as $4 \times 4 = 4^{2}$. So, $\sqrt{16} = (16)^{\frac{1}{2}} = (4^{2})^{\frac{1}{2}} = 4$.

This guide will cover how to calculate the square root of 16 in detail, along with lots of related examples.

What Is 16 Square Root?

The square root of a given number is a number multiplied by itself to generate the answer. Consider two real numbers, x and y if:

$x^{2} = y$

$x = \sqrt{y}$

In the above equation, “$x$” is the square root or the second root of “$y$.” So this means that if we multiply “$x$” by itself, it gives us the square of “$y$.”

The square root of $16$ is $4$, so by definition, if we multiply $4$ by itself, we should get $16$, and we know $4\times 4$ is = $16$. All the values generated by multiplying with themselves are known as a perfect square; hence the number 16 is also a perfect square.

The square root of the number $16$ is equal to $4$.

The exponential representation of square root of $16$ can be written as $(16)^{\frac{1}{2}}$ or $(16)^{0.5}$

How To Calculate Square Root of 16

We can determine the square root of 16 using two different methods, and the names of these methods are mentioned below.

1. Prime Factorization Method

2. Long Division Method

Prime Factorization Method

Let us study the steps involved in the prime factorization method to solve the square root of 16.

Step 1: In the first step, we will write down the factors of 16, and we can write factors of 16 as

$16 = 2 \times 2 \times 2 \times 2$

Step 2: In the second step, we combine two pairs and will write the equation as

$16 = 4 \times 4 or (2\ times 2)^{2}$

Step 3: In the third step, we write the factors in the final exponential form

$16 = 4\times 4 = 4 ^{2}$

Step 4: In the final step we take square root of the both sides

$\sqrt{16} = \sqrt{4^{2}}$

$\sqrt{16} = 4$

Long Division Method

Let us now study the second method, which is used to calculate the square root of $16$, called the long division method. The steps involved in the long division method to solve the square root of $16$ are given below:

Step 1: In the first step, we write the number $16$ under the bar as we do for all numbers for which we want to apply the division method.

Step 2: In the second step, we will find out the largest number, which, when multiplied by itself, will generate 16, and in this example, that number is $4$.

Step 3: In the third step, we perform the division by choosing $4$ as the divisor and $4$ as the quotient.

Step 4: The quotient we obtained in step $3$ will be the square root of the number $16$.

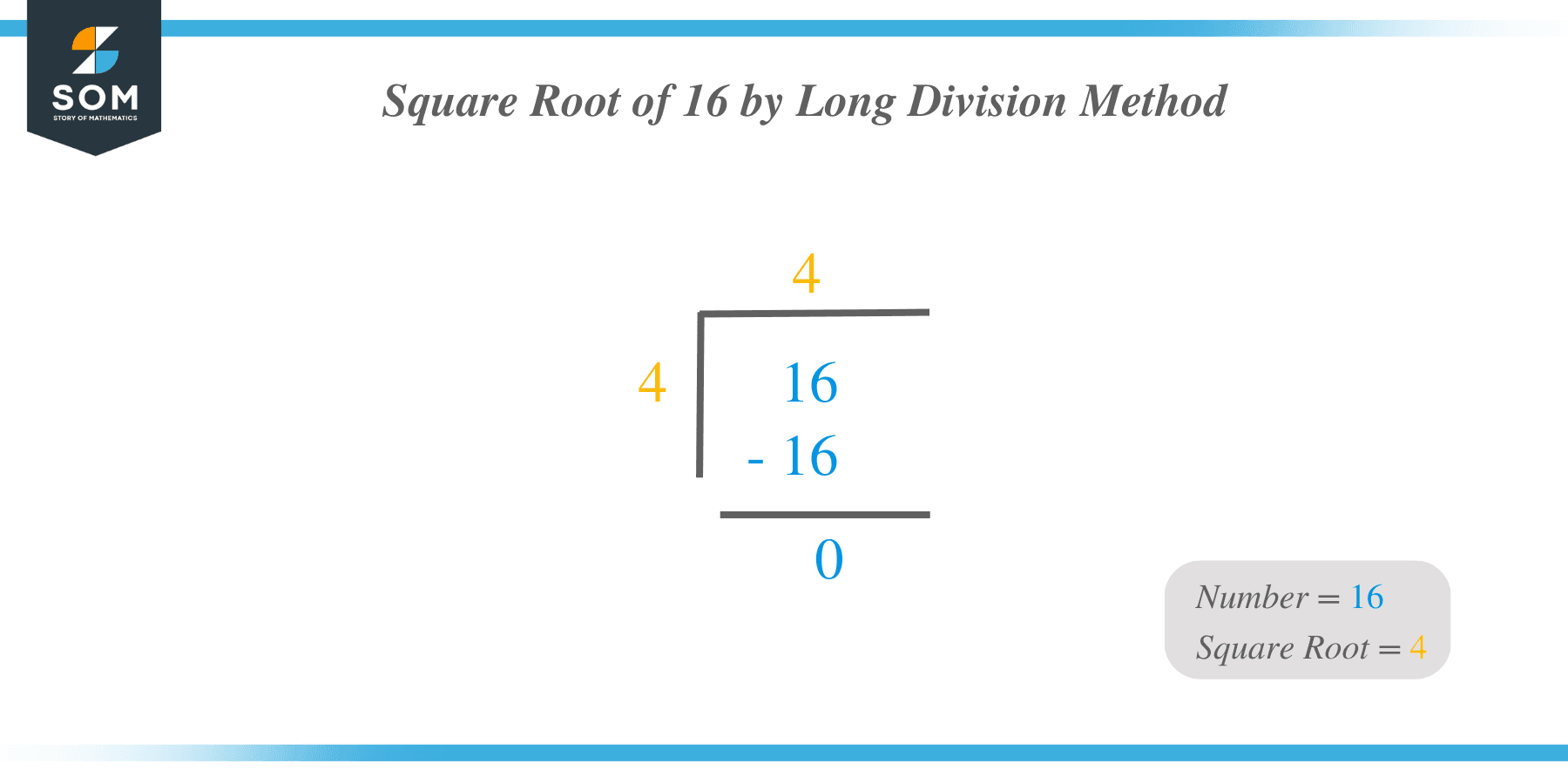
Example 1

Find the area of the square

Solution:

The area of the square = $a \times a$

$= \sqrt{4}.\sqrt{4} = 2 \times 2 = 4$

Area of the square$= \sqrt{4} = 2$

Example 2

Find the area of the square

Solution:

The area of the square = $a \times a$

$= \sqrt{4\times 4}$

$= \sqrt{16} = 4$

Example 3

Allan has different color cube boxes in his toy box. If five of the cube boxes are red and six of the cube boxes are blue, and he uses all of them to form a big square, what will be the number of bricks on each side of the square box?

Solution:

First, we will calculate the total amount of cubes used by Allan.

The total amount of cubes $= 9 + 7 = 16$

Now we calculate the cubes on each side of the surface

Cubes on each side of surface $= \sqrt{16} = 4$.

So, the bricks required on each side of the square box will equal $4$.

Example 4

If the area of an equilateral triangle is given as $4\sqrt{3}$, what will be the length of all sides of the triangle?

Solution:

We know that all sides of one equilateral triangle are equal in length, and if we find out the length of one side of the triangle, that will be equal to the rest of the two sides.

If one side of the triangle is “x,” then we can write the formula for the area of the triangle as

Area $= \dfrac{\sqrt{3}}{4}  .x^{2}$

We are given the value of the area of the triangle, plugging in the value in above equation

$4\sqrt{3} = \dfrac{\sqrt{3}}{4}  .x^{2}$

$x^{2} = 16$

$x = \sqrt{16} = \pm 4$

and as we know the length of triangle cannot be negative, hence the length of all sides of triangle is $4$ units each.

Tips for Solving the Square Root of a Number

Let us discuss some tips you can use while trying to solve problems related to the square root of the fractions.

Practice

It is very important to practice different problems related to the square root of a number. Solving different questions will increase your mathematical skills and make you feel more comfortable solving problems related to square roots.

Seek Help If Necessary

When you find it challenging to solve different problems related to square roots, feel free to seek help. You can seek help through an online square root calculator or ask your teacher or friends. You can also visit our article for the calculation of square root in detail.

Re-Check Your Work

When solving any mathematics problem, you must cross-check what you have just solved. Maths provide you with back substituting methods, factorization, and other methods to verify your answer. The same goes for solving problems related to square roots; you can easily verify the solution by using the calculator. If your answer does not match the calculator’s answer, you should go back, find the mistake and correct it.

The second way to re-check your answer is to perform the same calculation again, and if you have extra time on your hands, you can do the same calculation three times to ensure you have solved the question correctly. This is a good practice, and it will help in solving all types of mathematical problems, and you will develop a good habit of re-checking your work.

Examples

1. Is 16 a Perfect Square Root?

Answer: Yes, it is, as the answer of the square root of $16$ is an integer. Numbers like $4$, $16$, $254, $49$, $64$ etc are all perfect squares number. Any number that is multiplied by itself will give a perfect-square number.

For prime numbers like $5,7 where we cannot generate 11$ by multiplying by the two same numbers, these types of numbers are called non-perfect squares.

2. What Is the Square Root of -16?

Answer: The square root of $-16$ is an imaginary number and is equal to $4i$. We know that $i = \sqrt{-1}$. Hence, $\sqrt{16}$ can be written as $\sqrt{16}\times \sqrt{-1}$, which in turn is equal to $4i$. Remember 4i is not a real number. The square roots of negative number are always imaginary numbers.

3. Why the Square Root of 16 Is Only +4, and Not +4 and -4?

Answer: This is a tricky question and people often get confused while solving it and simple answer to the question is, yes the square root of $16$ is only $+4$ and not $+4$ and $-4$ simultaneously.

You will often see answers saying that $-4 \times -4$ is also $16$ while $+4 \times +4$ is also 16 so the square root of $16$ is $+4$ and $-4$.

Basically, students confuse $\sqrt{16}$ with $x^{2} =16$.

The answer for $\sqrt{16} = 4$ while the answer for $x^{2} = 16$ is $+4$ and $-4$ as it is a quadratic equation and will have two solutions. In mathematics, when you are asked to find the range of the function $f(x) = \sqrt{x}$, the answer would be all the real numbers greater than zero, and as you can see no negative numbers are mentioned. So it proves that answer of $\sqrt{16}$ is only $+4$.

4. What Is the Square Root of 25?

Answer: The square root of the number 25 is 5.

5. What is the Square Root of 36?

Answer: The square root of the number 36 is 6.

6. What Is the Square Root of 100?

Answer: The square root of the number 100 is 10.

7. What is the Square Root of 225?

Answer: The square root of the number 225 is 15.

8. What Is the Square Root of 8?

Answer: The square root of the number 8 is 2\sqrt{2}.

9. What Is the Square Root of 11?

Answer: The square root of the number 11 is 3.3126.

Conclusion

Let us write down the concluding remarks about what we have learned so far.

• The square root of 16 is 4.

• To find the square root of a number, we can use two methods a) Prime Factorization and b) Long Division method.

• In Prime Factorization, we write down the factors of 16 and then combine them to form the exponential form and take the square root of both sides.

• In the Long Division Method, we multiply the divisor and the quotient (which are equal to each other) to get the square root of the number.

Understanding the concept of finding the square of $16$ will be much easier after having gone through this guide.