JUMP TO TOPIC

To graph polynomials, I always begin by identifying the polynomial function and its degree. The degree gives me valuable insight into the overall shape of the graph.
For instance, if I have a second-degree polynomial like $(f(x) = ax^2 + bx + c)$, I know the graph is a parabola. When graphing higher-degree polynomials, such as $(f(x) = ax^n + … + k)$, where (n) is a positive integer, I look for turning points, which are one less than the degree of the polynomial.
My next step involves finding the roots of the polynomial, which are the values of (x) that make (f(x) = 0). These correspond to the x-intercepts of the graph on a Cartesian plane.
Factoring the polynomial helps to find these roots easily. If the polynomial cannot be factored, I use numerical methods or graphing tools to estimate them.
By sketching a rough outline based on the degree and roots, I consider the leading coefficient to determine the end behavior of the graph. This tells me where the arms of the polynomial go at extreme values of (x); that is, as (x) approaches positive or negative infinity.
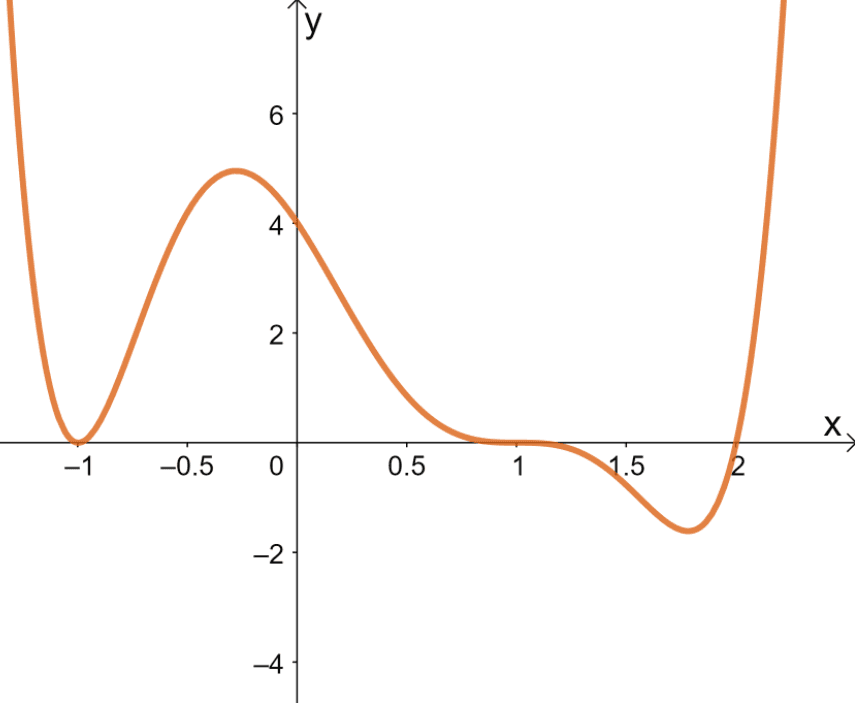
Steps Involved in Graphing Polynomials
Graphing polynomials is a straightforward process when you follow these steps.
I’ll detail how to sketch the graph of a polynomial function by hand.
Determine the Degree and Leading Coefficient
- Find the degree of the polynomial. It’s the highest power of the variable in the equation.
- Identify the leading coefficient (the coefficient of the term with the highest power).
Analyze End Behavior
- Use the degree and the leading coefficient to predict the end behavior of the function. If the degree is odd and the leading coefficient is positive, the graph starts low and ends high.
Find the X- and Y-intercepts
- Solve the equation (f(x)=0) to find the x-intercepts or zeros.
- Substitute (x=0) to find the y-intercept.
| Step | What to look for |
|---|---|
| Degree & Leading Coefficient | The degree indicates how many turns; the leading coefficient suggests initial end behavior. |
| Zeros & Multiplicity | Zeros give x-intercepts; multiplicity hints if the graph touches or crosses the x-axis. |
| X-intercepts | Solve (f(x)=0) for all values of (x). |
| Y-intercept | Calculate (f(0)) for the y-intercept. |
Plot the Intercepts
- Place the intercepts on the graph. Remember, for zeros of even multiplicity, the graph touches the x-axis, and for zeros of odd multiplicity, it crosses the x-axis.
Draw and Refine the Graph
- Knowing that a polynomial function is continuous, draw a smooth curve through the intercepts, respecting the end behavior.
- Check for symmetry if applicable; an even degree may indicate the graph is symmetrical about the y-axis.
Remember, while graphing, keep the curve smooth since polynomial functions do not have breaks or sharp turns.
Advanced Concepts
In graphing polynomials, one of my key considerations is identifying turning points.
These are points where the graph changes direction, and they’re essential for understanding the local behavior of the function. I use calculus to find turning points by setting the first derivative to zero and solving for the x-values.
Symmetry plays a role, too. If a function is even, its graph is symmetric about the y-axis, and if it’s odd, it’s symmetric about the origin. To check for symmetry, I substitute $-x$ for $x$ and see if I get the original function or its negative.
When I utilize technology like graphing calculators or computer software, I can quickly visualize the function and its properties. This is incredibly useful when dealing with complex polynomials that are not easily graphed by hand.
Here’s a quick table summarizing the checks for symmetry in polynomials:
| Test for Symmetry | Result |
|---|---|
| $f(-x) = f(x)$ | Symmetric about y-axis (Even function) |
| $f(-x) = -f(x)$ | Symmetric about origin (Odd function) |
When modeling real-world scenarios with polynomials, I ensure that my polynomial function accurately represents the data. For example, if I’m given a table of values, I can derive a polynomial that passes through those points using methods like polynomial interpolation.
In summary, graphing polynomials involves pinpointing turning points, assessing symmetry, utilizing technology for visualization, and ensuring the model suits the given data. By understanding these advanced concepts, I can unlock a deeper comprehension of polynomial behavior.
Real-World Applications
When I explore real-world applications of polynomials, their versatility truly shines. For instance, imagine a cable company determining its expected revenue for the upcoming years. Polynomials allow this company to create a model that predicts financial outcomes.
The shape of the graph of a revenue polynomial provides insights that are crucial for business planning.
For example, consider a polynomial representing revenue in millions of dollars against time in years. The x-values can represent the year, and the output gives the projected revenue.
Let’s say a revenue function is modeled as ( R(t) = -0.037t^4 + 1.414t^3 – 19.777t^2 + 118.696t – 205.332 ), where ( R ) represents the revenue in millions of dollars and ( t ) is the year with ( t = 6 ) corresponding to 2006.
By graphing this polynomial, I can identify the years of high and low revenue and plan accordingly.
| Year (t) | Revenue ( R(t) ) (in millions) |
|---|---|
| 6 | ( R(6) ) |
| 7 | ( R(7) ) |
| 8 | ( R(8) ) |
Further, the visual representation aids in understanding at which points revenue increases or decreases, which can signal when to invest in marketing or expansion.
Understanding these patterns is valuable to both business strategists and economists who regularly employ polynomials to analyze and predict economic growth trends.
Conclusion
In graphing polynomial functions, my approach has been systematic, emphasizing the importance of understanding the core concepts such as zeros, multiplicities, end behavior, and intercepts.
Remember that zeros of odd multiplicity mean the graph will intersect and pass through the x-axis at those points, whereas even multiplicity indicates a touch and turn at the axis without crossing.
Identifying the degree of the polynomial is crucial because it influences the end behavior of the graph. A fundamental concept to remember is that the degree of the polynomial indicates the maximum number of turns the graph can take.
As a brief recap, for a polynomial function $ f(x) $, the end behavior is determined by the leading coefficient and the degree of the function. If the degree is odd and the leading coefficient is positive, as $ x \rightarrow \infty $, $ f(x) \rightarrow \infty $ and as $ x \rightarrow -\infty $, $ f(x) \rightarrow -\infty $.
Make use of the Intermediate Value Theorem to understand how polynomial functions behave between given points. This is especially useful to verify the existence of roots or zeros within certain intervals.
As you continue to practice and apply these principles in graphing polynomials, I trust you’ll find a growing confidence in interpreting and sketching these functions on your own.
The coherence between the algebraic form and graphical representation of polynomials is a powerful tool in the study and application of mathematics.
