JUMP TO TOPIC
Math Transformations — Explanation and Examples
 Math transformations relate one geometric object or function to another through a series of translations, rotations, reflections, and dilations.
Math transformations relate one geometric object or function to another through a series of translations, rotations, reflections, and dilations.
Depending on the context, math transformations are sometimes called geometric transformations or algebraic transformations.
Although it is possible to do some transformations in pure geometry, most math transformations occur in coordinate geometry. Make sure to review both before proceeding.
This section covers:
- What are the Four Types of Transformations?
- How to Do Transformations in Geometry
What are the Four Types of Transformations?
Transformations are broken down into four different types: translations, rotations, reflections, and dilations. If it is possible to map one object onto another using any combination of transformations, the objects are said to be similar.
Translations
A translation slides an object up, down, left, or right.
Translations can be represented through words, such as “an object is translated two units downward,” or through mapping notation. Mapping notation is a shorthand way of showing how a function or point changes with a transformation.
For example, $(x, y) → (x+1, y-4)$ means that the x-coordinate of every point in an object will increase by one, and the y-coordinate of every point in an object will decrease by four. Effectively, the object will move one unit to the right and four units downward.
Mapping notation for a function is $f(x)$ → $f(x-a)+b$. This means that the function moves $a$ units to the right and $b$ units upward. If $a$ is negative, the function moves left, and, if $b$ is negative, the function moves downward.
As before, the x-values of functions operate in a “mirror world” of sorts where transformations done directly to $x$ are the opposite of what is expected. That is, positive numbers indicate a shift to the right, while negative numbers indicate a shift to the left.
Rotations
Rotational transformations move a geometric object about a fixed point in the plane.
To visualize how a rotation works, picture an invisible string connecting each point in the given object to the point of rotation. Then, imagine moving this string a certain angle measure clockwise or counterclockwise, keeping the point of rotation fixed and only moving the end that is part of the geometric object. The new positions of the points in the original object represent a rotational transformation.
Rotations can be given in degrees or radians, and they can be done clockwise or counterclockwise.
For example, A’B’C’ is the rotation of ABC 90 degrees about the origin.
Reflections
When you look in the mirror, you see your reflection. That is, you see a backward image of yourself. The version of yourself appears closer to the glass when you are closer to the glass and farther away when you are farther away.
A mathematical reflection is similar. We select a line in the plane and treat it like a mirror. Everything on one side of the line is the mirror image of everything on the other side.
The most common lines of reflection are the x-axis, the y-axis, and the line $y=x$.
Dilation
A dilation expands or contracts a geometric object to create a new, scale object with the same proportions. Note that the term dilation refers only to an expansion in some contexts, while the term compression refers to a shrinkage. Here, however, we will use it to mean both.
A dilation needs a scale and a fixed point. A scale greater than one indicates that the object will increase in size, while a scale less than one indicates that an object will decrease. The dilation factor must always be greater than zero.
The fixed point in a dilation orients the object. It indicates the one point that stays the same. Often, it is the vertex or center of an object.
For example, you can think of a circle with a radius of 1 and another circle with a radius of 2. Suppose both are centered at the origin. The second circle is a dilation of the first by a factor of 2 with a fixed center point. Likewise, the first is a dilation of the second by a factor of $\frac{1}{2}$ with a fixed center point.
How to Do Transformations in Geometry
Geometric transformations often combine more than one type of transformation.
The easiest way to do transformations in geometry is to find the new key points’ location and use those to find other points.
For example, when transforming a triangle, first map the vertices to their new location. Then, draw the lines connecting the vertices.
Alternatively, when transforming a function, find the key points such as the x- and y-intercepts and the vertex. This will show the function’s general shape, and all that’s left to do is connect the dots.
Examples
This section covers common examples of problems involving math transformations and their step-by-step solutions.
Example 1
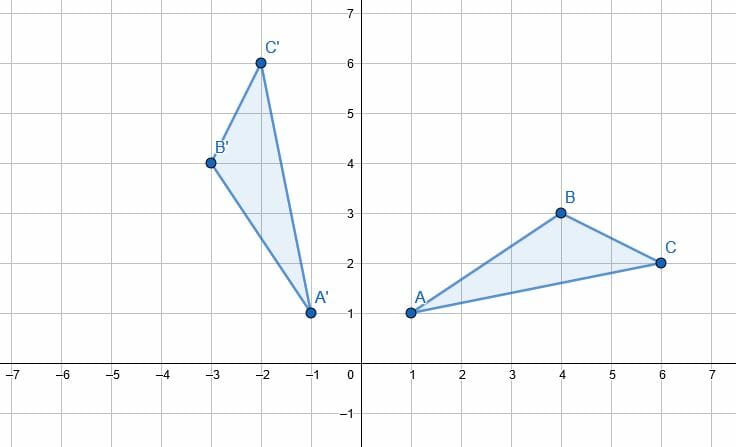
What transformations are required to map triangle ABC to DEF?
Example 1 Solution
The wording of this problem actually gives an important clue to the solution. The triangle ABC maps to DEF. Therefore, point A maps to D, B maps to E, and C maps to F. Thus, the problem boils down to “how do we map the vertices of ABC to the corresponding vertices in DEF?”
First, note that the triangle DEF has a different orientation from ABC. This means that either a rotation or a reflection is involved. However, since DEF is the mirror image of ABC and not just a rotation, we know a reflection is involved. Since the mirror image is horizontal, the most likely line of reflection is the y-axis.
Reflecting ABC over the y-axis makes the x-value of all of the vertices negative. That is, the reflection A’B’C’ has the coordinates (-2, 1), (-3, 4), and (-7, 3), respectively.
Then, A’B’C’ and DEF are related by a translation. In this case, moving the triangle down two units maps the first to the second.
Therefore, the series of transformations reflect the y-axis followed by a translation two units downward.
Note, however, that this is not unique. If instead, the ABC shifts down two units and then reflects over the y-axis, it still maps to DEF. Likewise, reflecting ABC over any vertical line x=k, where k<2, including a horizontal translation, works.
Example 2
What transformations are required to map $f(x)$ to $g(x)$?
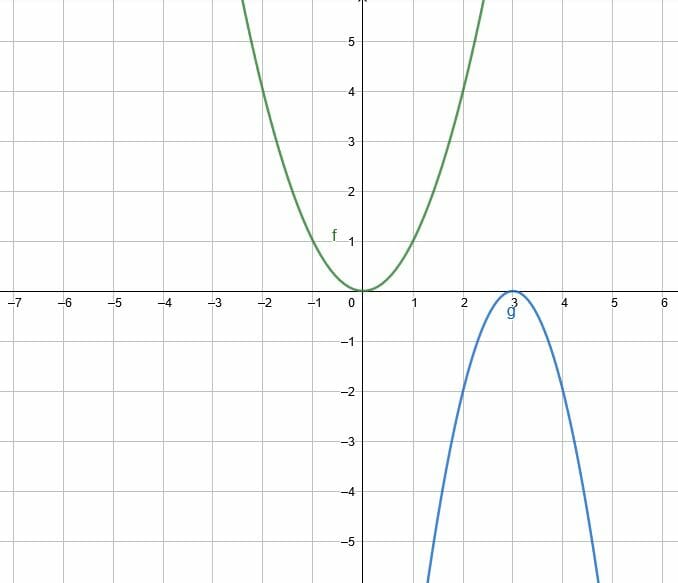
Example 2 Solution
In this example, $f$ and $g$ are both quadratic functions. The difference is that $g$, relative to $f$, is upside down, further right, and thinner.
These three facts indicate the transformations. The fact that $g$ is upside down relative to $f$ means that it has been reflected over the x-axis.
Since $g$ is further right, there is a translation of three units to the right.
Finally, since $g$ is stretched vertically, there is a dilation by a factor greater than 1. In this case, the factor is 2.
Example 3
What is the relationship between a rotation and a reflection? Are there any situations where they might be the same?
Example 3 Solution
Objects with internal lines of symmetry may map to the same figure through rotation and reflection.
For example, consider an isosceles triangle with vertices ABC at (2, 0), (0, 4) and (-2, 0). This triangle is symmetric about the y-axis.
A reflection over the x-axis followed by a reflection over the y-axis gives the triangle DEF with vertices at (-2, 0), (-4, 0), (2, 0).
Likewise, a rotation of ABC about the origin 180 degrees also yields the same triangle DEF.
Note that the reflection over the y-axis is necessary because, otherwise, the triangle ABC corresponds to FED instead. That is the point A maps to F, and point C maps to D.
Example 4
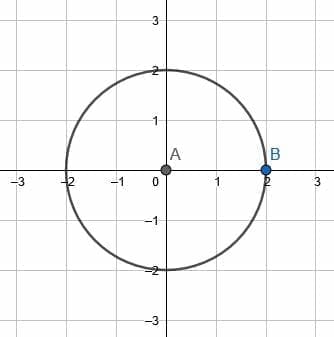
Compare a rotation of the circle about the center to a rotation about point B.
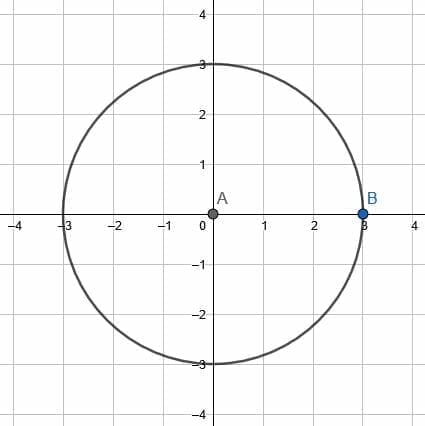
Example 4 Solution
It should be pretty clear that rotating a circle about its center results in the circle’s points being mapped to other points on the circle. That is, the new figure will have the same shape and coordinates.
If, for example, the circle rotated about the center counterclockwise by 90 degrees, point B would end up at (0, 3) instead of (3, 0). If no points on the circumference are given, however, the figures will be indistinguishable.
On the other hand, however, a rotation about point B causes the circle to move to different places on the plane. The center of the circle will carve out its own circle with center B and radius 3.
Example 5
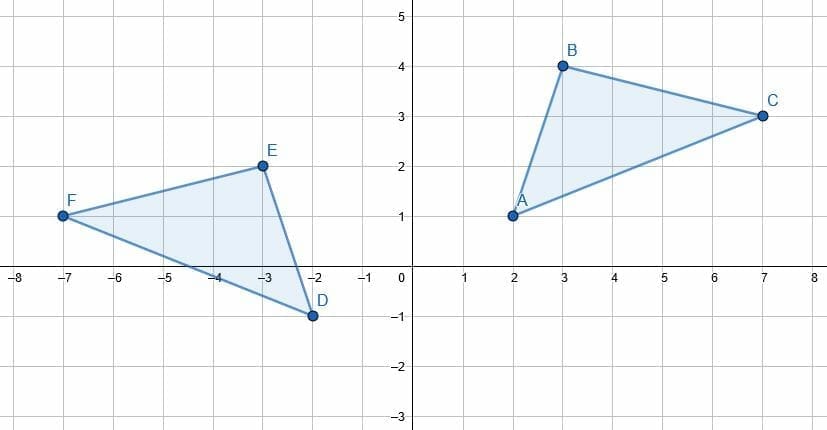
Does the transformation from ABC to FDE represent a translation? How do you know?
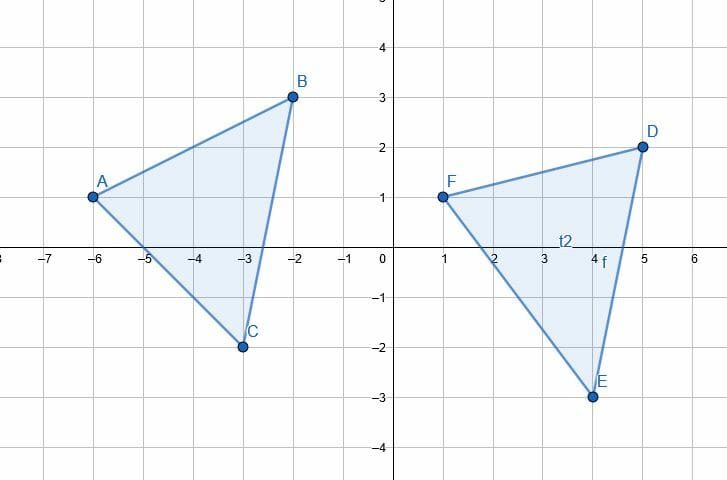
Example 5 Solution
This does not represent a translation because a translation keeps the shape of the original figure. In fact, that is why translations (along with rotations and reflections) are called “rigid transformations.”
In the new figure, FD has a slope of $\frac{1}{4}$. However, the slope of AB in the original figure is $\frac{1}{2}$.
Practice Questions
![]()
Open Problems
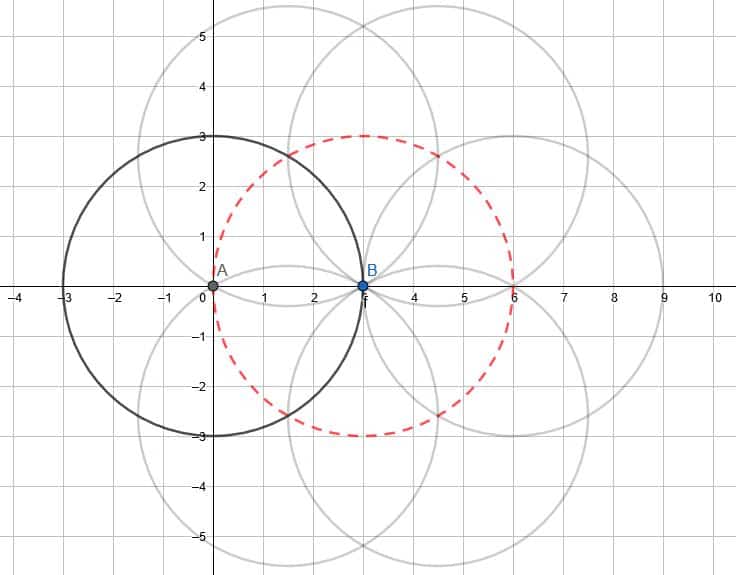
- Compare a dilation of the circle by a factor of $2$ with the center of rotation at $A$ and a dilation by a factor of $2$ with the center of dilation $B$.

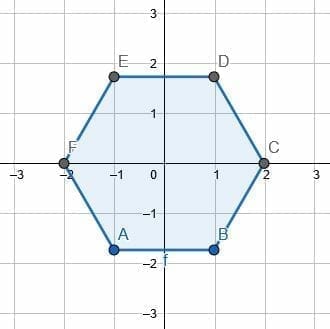
- Consider the hexagon ABCDEF. Which transformations map the points on the hexagon onto other points on the original hexagon?

Open Problem Solutions
1.
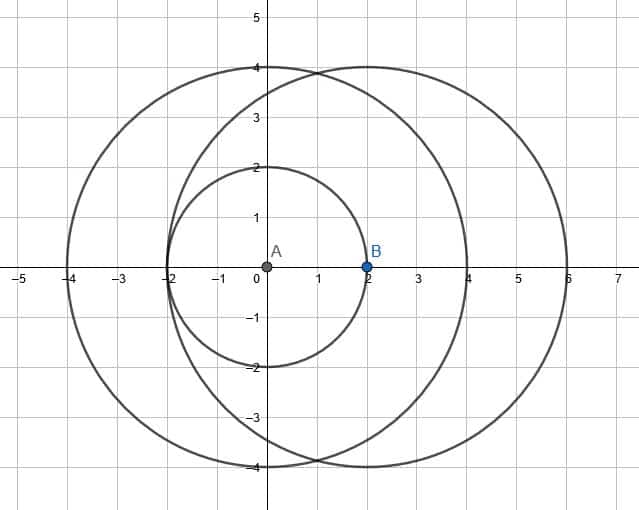
2.
Rotations about the center by 180/6=30 degrees and reflections about any line connecting two opposite vertices or the centers of opposite edges will map the points on the hexagon to other points on the hexagon.
Images/mathematical drawings are created with GeoGebra.