JUMP TO TOPIC

The Hyperbolic paraboloid is a captivating geometric shape that exhibits a unique and visually intriguing structure. Defined by its distinct curving, saddle-like surface, the hyperbolic paraboloid is a fascinating object of study in mathematics, architecture, and engineering. This geometric form is characterized by two families of intersecting lines, resulting in a surface that possesses both concave and convex curvatures. The hyperbolic paraboloid’s dynamic and visually striking appearance has made it a popular choice in architectural designs, offering not only aesthetic appeal but also structural advantages.
In this article, we will delve into the fundamental properties, architectural applications, and mathematical concepts behind the hyperbolic paraboloid, shedding light on the captivating nature of this geometric marvel.
Definition
A hyperbolic paraboloid is a type of quadratic surface in three-dimensional space that belongs to the category of conic sections. This surface is represented by the equation z = ax² – by², where a and b are constants, and x, y, and z are the variables representing the three dimensions of space.
A hyperbolic paraboloid’s distinctive ability to curve upwards along one axis and downwards along the other is what gives it its distinctive “saddle” shape. This sets it apart from other varieties of paraboloids, including the elliptical paraboloid, which has identical signs in front of the equation’s x² and y² terms. Below we present a generic structure of a parabolic hyperboloid.
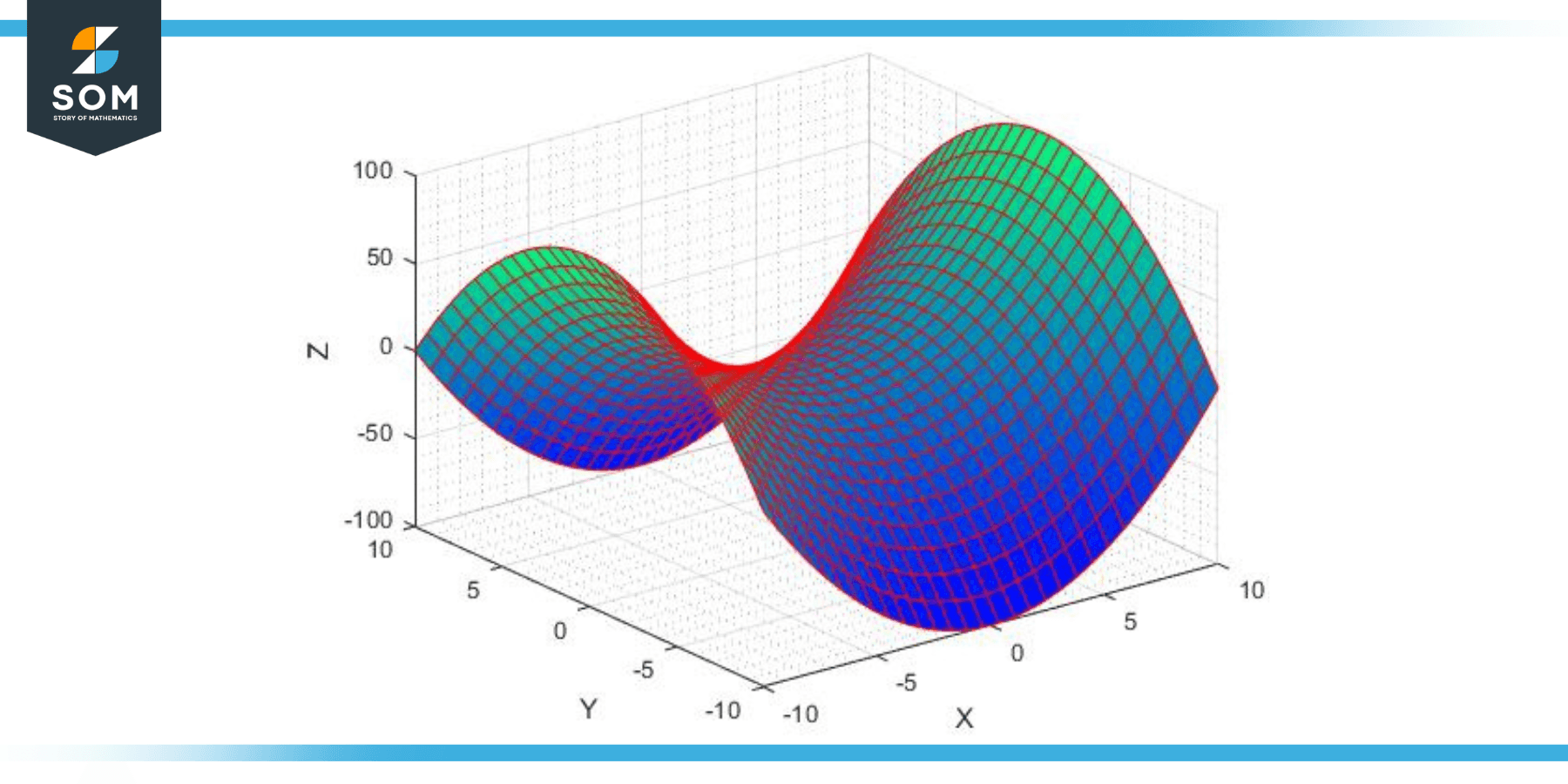
Figure-1. A generic hyperbolic paraboloid structure.
One of the most significant properties of a hyperbolic paraboloid is that it is a doubly ruled surface, meaning there are two distinct sets of straight lines, or rulings, that lie entirely within the surface. This property has practical applications in fields such as architecture and engineering, where it is used to construct structures that are both lightweight and robust.
Historical Significance
The Hyperbolic paraboloid has a notable historical background that spans various fields of study and application. Its development can be dated to the late 19th and early 20th centuries, when it became popular in engineering, mathematics, and architecture.
Mathematically, the hyperbolic paraboloid was explored within the realm of differential geometry. During the 19th century, pioneering mathematicians like Jean-Baptiste Listing and Carl Friedrich Gauss significantly influenced the study of curved surfaces and the growth of differential geometry.
The importance of the hyperbolic paraboloid in terms of architecture first became apparent at the height of the Modernist movement in the early 20th century. Architects and designers sought to break away from traditional architectural forms and explore new possibilities for structure and aesthetics. This led to the exploration and utilization of unique geometries, including the hyperbolic paraboloid.
One prominent figure associated with the introduction of the hyperbolic paraboloid in architecture is the Hungarian architect Félix Candela. In the mid-20th century, Candela became known for his innovative use of reinforced concrete to create lightweight and thin-shell structures. He extensively employed the hyperbolic paraboloid as a fundamental element in his architectural designs, showcasing its structural efficiency and aesthetic appeal.
The hyperbolic paraboloid’s architectural applications extended beyond Candela’s work. Its adoption by architects such as Antoni Gaudí, Frei Otto, and Buckminster Fuller further popularized its use in various architectural styles, including Modernism, Expressionism, and Organic Architecture.
Over time, advancements in computer-aided design and engineering have allowed for even greater exploration and implementation of the hyperbolic paraboloid in diverse fields. Its versatile nature and visually striking appearance continue to inspire architects, engineers, and designers, shaping modern architectural and structural landscapes.
The historical journey of the hyperbolic paraboloid, from its mathematical origins to its integration into architectural and engineering practices, showcases its enduring influence and relevance as a captivating geometric form.
Types
In terms of their geometric description, hyperbolic paraboloids are not classified into specific types. The term “hyperbolic paraboloid” refers to a particular type of quadratic surface that has a consistent set of properties.
However, there are variations in the orientation of the hyperbolic paraboloid depending on the coefficients in its defining equation, z = ax² – by². These coefficients can lead to the “opening” of the paraboloid in different directions.
Positive Coefficient Hyperbolic Paraboloid
If both a and b are positive, then the paraboloid opens upwards along the x-axis and downwards along the y-axis.
Negative Coefficient Hyperbolic Paraboloid
If both a and b are negative, the paraboloid opens downwards along the x-axis and upwards along the y-axis.
In both these cases, the surface still has the same saddle shape and retains all the key properties of a hyperbolic paraboloid, including being a doubly ruled surface and having negative Gaussian curvature.
In terms of applications, hyperbolic paraboloids can be categorized based on their usage:
Architectural Hyperbolic Paraboloids
In architecture, hyperbolic paraboloids are used as roofs and other architectural features due to their strength and aesthetic properties. Examples include the roof of the Saddledome in Calgary, Canada, and the roof of St. Mary’s Cathedral in Tokyo, Japan.
Mathematical Hyperbolic Paraboloids
In mathematics, hyperbolic paraboloids are studied for their interesting geometric and topological properties. They are often used as examples in multivariable calculus and differential geometry courses.
Graphical Hyperbolic Paraboloids
In computer graphics, hyperbolic paraboloids can be used as surface patches in 3D modeling and rendering. These surfaces can be defined and manipulated with a relatively simple set of parameters, making them useful for creating complex shapes.
It’s important to note that all of these “types” are still hyperbolic paraboloids and share the same basic properties. The categorization is more about the context in which the hyperbolic paraboloid is used rather than any intrinsic difference in the shape itself.
Properties
Absolutely! The hyperbolic paraboloid is a captivating geometric shape with several unique properties that make it a focus of interest in both theoretical mathematics and practical applications.
Quadratic Surface
A hyperbolic paraboloid is a type of quadratic surface, which means it’s surface in three-dimensional space that can be described by a second-degree equation. In the case of a hyperbolic paraboloid, this equation is z = ax² – by², where a and b are constants.
Saddle Shape
One of the most recognizable features of a hyperbolic paraboloid is its distinctive ‘saddle’ shape. The surface curves upwards in one direction and downwards in the other, giving it a concave and convex form. This form is determined by the opposite signs in front of the x² and y² terms in its defining equation.
Doubly Ruled Surface
Hyperbolic paraboloids are doubly ruled surfaces. A ruled surface is a surface that can be generated by moving a line (called the generator) along a path. For a hyperbolic paraboloid, there are two distinct families of lines that lie entirely on the surface. You can move a line along two different paths and cover the entire surface, which is not possible with most other surfaces. Each line in one family intersects each line in the other family exactly once.
Asymptotic Directions
Another geometric property related to the hyperbolic paraboloid is the presence of asymptotic directions at each point on the surface. These are the directions along which the surface bends least. For the hyperbolic paraboloid, the asymptotic directions are along the lines of the ruling families.
Parabolic and Linear Cross-Sections
The cross sections of a hyperbolic paraboloid reveal more of its geometric properties. Any cross-section parallel to the z-axis is a parabola, while cross-sections parallel to either the x-axis or y-axis are straight lines. This property combines linear and parabolic features in a single shape, further enhancing its geometric complexity and beauty.
These properties give the hyperbolic paraboloid a blend of complexity and simplicity that make it a fascinating object of study in geometry. These characteristics also make it incredibly useful in practical applications such as architectural design, where its structural properties can be leveraged to create robust, aesthetically pleasing structures.
Ralevent Formulas
A hyperbolic paraboloid is defined by its characteristic equation and has properties that can be derived from it. Here are some of the key mathematical aspects associated with this geometric shape:
Defining Equation
The general equation for a hyperbolic paraboloid is z = ax² – by² + cz + d = 0, where a, b, c, and d are constants. The a and b terms are opposite in sign, which gives the hyperbolic paraboloid its distinctive saddle shape.
Ruled Surface Lines
The hyperbolic paraboloid is a doubly ruled surface, meaning it contains two distinct sets of straight lines. The parametric equations for these lines can be derived from the general equation of the surface. For the hyperbolic paraboloid z = x² – y², the two families of lines are given by the parametric equations (x, y, z) = (t, t² – s², 2 × s × t) and (x, y, z) = (t, s² – t², 2 × s × t). These families of lines intersect each other to form the hyperbolic paraboloid.
Partial Derivatives
The partial derivatives of a hyperbolic paraboloid can be used to examine its slope and curvature. The partial derivatives with respect to x and y for the equation z = ax² – by² are ∂z/∂x = 2ax and ∂z/∂y = -2by, respectively. These represent the rate of change of z with respect to x and y.
Principal Curvatures
The principal curvatures of a hyperbolic paraboloid, denoted as k1 and k2, are a measure of the amount of bending of the surface in different directions. For the hyperbolic paraboloid z = x² – y², the principal curvatures are $k_1 = \frac{-1}{(2 \times (1+y^2))^{\frac{3}{2}}}$ and $k_2 = \frac{1}{(2 \times (1+x^2))^{\frac{3}{2}}}$.
Gaussian Curvature
The Gaussian curvature, K, is a measure of the intrinsic curvature of a surface. For the hyperbolic paraboloid z = x² – y², the Gaussian curvature is K = -4/(4 + 4x² + 4y²)². Notably, the Gaussian curvature of a hyperbolic paraboloid is negative, which is a characteristic of all saddle-like surfaces.
Mean Curvature
The mean curvature, H, is another measure of a surface’s curvature. For the hyperbolic paraboloid z = x² – y², the mean curvature is H = 0. This means that the hyperbolic paraboloid is a minimal surface, which is a surface that locally minimizes its area.
These mathematical formulas help us delve into the properties and characteristics of the hyperbolic paraboloid, providing a deeper understanding of its geometry. This geometry finds its applications in various domains, such as architecture, physics, and computer graphics, proving the mathematical intricacy and utility of the hyperbolic paraboloid.
Applications
The Hyperbolic paraboloid finds versatile applications in various fields, ranging from architecture to engineering and beyond. Its unique geometry and structural properties make it a valuable element in diverse applications. Let’s explore some of the key fields where the hyperbolic paraboloid finds application:
Architecture and Design
The hyperbolic paraboloid’s visually striking form and structural efficiency make it a popular choice in architectural design. It is commonly used in the construction of roofs, shells, canopies, and pavilions. Its double-curvature surface allows for even distribution of loads, resulting in stable and aesthetically pleasing structures. Architects often utilize the hyperbolic paraboloid to create innovative, eye-catching designs that challenge traditional architectural norms.
Structural Engineering
The hyperbolic paraboloid’s inherent strength and stability make it ideal for structural engineering applications. Its double-curvature nature provides excellent load-bearing capabilities and resistance to external forces. The shape’s self-supporting properties eliminate the need for additional structural elements, reducing material and construction costs. Hyperbolic paraboloid structures are employed in bridges, roofs, shells, and other architectural elements where efficient load distribution is crucial.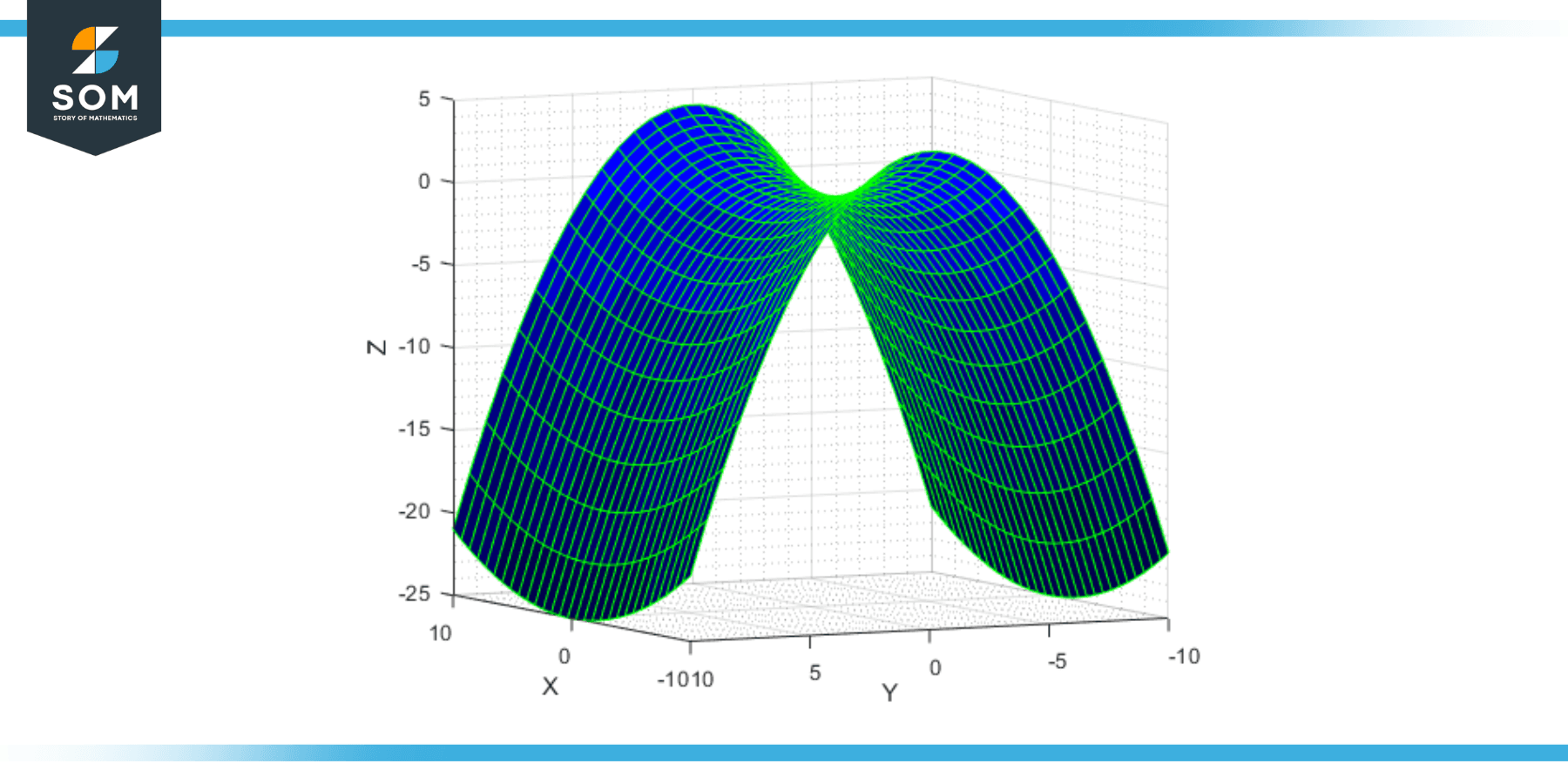
Figure-2. Hyperbolic paraboloid.
Acoustics and Sound Reflection
The unique geometry of the hyperbolic paraboloid lends itself to applications in acoustics. The shape’s curving surfaces help direct sound waves, making it useful for designing spaces with optimal sound reflection and diffusion. Hyperbolic paraboloid surfaces are commonly employed in concert halls, recording studios, amphitheaters, and other spaces where sound quality and diffusion are essential.
Mathematics and Geometry Education
Sculpture and Art Installations
The hyperbolic paraboloid’s captivating form and aesthetic appeal have attracted artists and sculptors. Its flowing lines and dynamic shape offer opportunities for creating visually engaging sculptures and art installations. Artists experiment with various materials to bring hyperbolic paraboloids to life, adding a sense of movement and intrigue to public spaces, galleries, and exhibitions.
Industrial Design and Product Development
The hyperbolic paraboloid’s elegant curves and structural properties have inspired its integration into industrial design. The shape’s versatility and strength make it suitable for creating furniture, lighting fixtures, consumer products, and other design elements. Industrial designers leverage the unique aesthetics of the hyperbolic paraboloid to create visually appealing and functional objects.
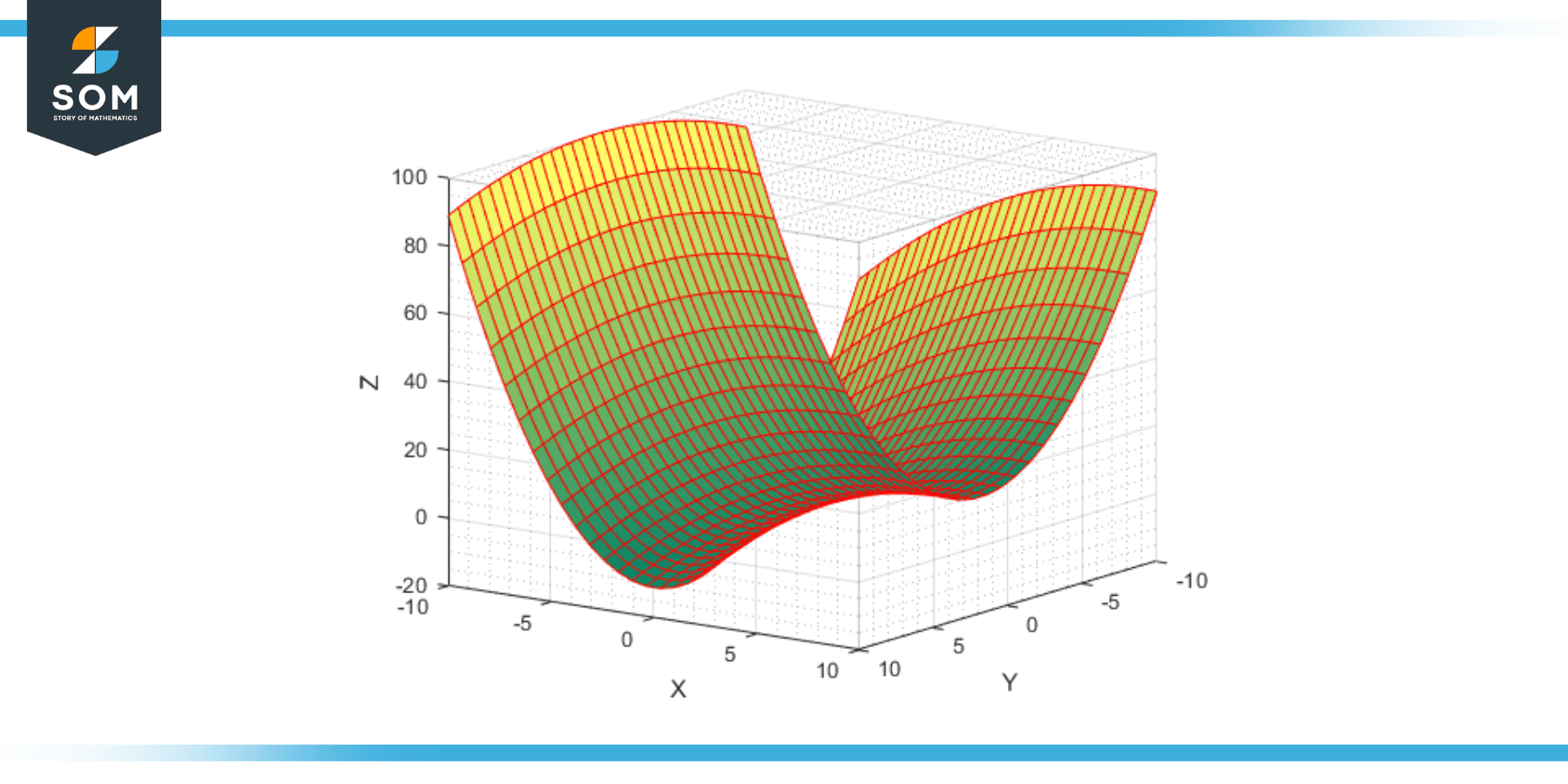
Figure-3. Hyperbolic paraboloid.
The applications of the hyperbolic paraboloid extend beyond the aforementioned fields, showcasing its wide-ranging utility and adaptability. As an architectural and geometric marvel, the hyperbolic paraboloid continues to inspire innovation and creativity in various domains, shaping the visual and functional landscapes of our built environment.
Exercise
Example 1
Identifying a Hyperbolic Paraboloid
Given the equation z = 3x² – 4y², determine if the surface is a hyperbolic paraboloid.
Solution
Since the equation has opposite signs for the x² and y² terms, it represents a hyperbolic paraboloid.
Example 2
The direction of the Opening
Given the equation z = -2x² + y², determine the direction of the opening of the hyperbolic paraboloid.
Solution
Since the coefficient of x² is negative, the paraboloid opens downwards along the x-axis and upwards along the y-axis.
Example 3
Ruled Lines
For the hyperbolic paraboloid given by z = x² – y², find the equations of the ruled lines.
Solution
The two families of lines for this hyperbolic paraboloid are given by:
(x, y, z) = (t, t² – s², 2 × s × t)
and
(x, y, z) = (t, s² – t², 2 × s × t)
Example 4
Partial Derivatives
Find the partial derivatives of the hyperbolic paraboloid defined by z = 3x² – 2y².
Solution
The partial derivatives with respect to x and y are ∂z/∂x = 6x and ∂z/∂y = -4y, respectively.
Example 5
Principal Curvatures
Compute the principal curvatures of the hyperbolic paraboloid defined by z = x² – y².
Solution
The principal curvatures are
$$k_1 = \frac{-1}{(2 \times (1+y^2))^{\frac{3}{2}}}$$
and
$$k_2 = \frac{1}{(2 \times (1+x^2))^{\frac{3}{2}}}$$
Example 6
Gaussian Curvature
Compute the Gaussian curvature of the hyperbolic paraboloid defined by z = x² – y²
Solution
The Gaussian curvature is K = -4/(4 + 4x² + 4y²)².
Example 7
Mean Curvature
Compute the mean curvature of the hyperbolic paraboloid defined by z = x² – y².
Solution
The mean curvature is H = 0.
Example 8
Surface Area
Compute an exact solution for the surface area of a hyperbolic paraboloid.
Solution
While finding an exact solution for the surface area of a hyperbolic paraboloid can be complicated due to the infinite extent of the surface, for a finite region, one can find the surface area using a double integral.
For instance, to find the area of the region of the hyperbolic paraboloid z = x² – y² bounded by the lines x = ±1 and y = ±1, one can set up and evaluate the double integral ∫∫√(1 + (2x)² + (-2y)²) dx dy over the region.
Note that this is a non-trivial calculation often reserved for advanced calculus courses.
All images were created with GeoGebra.
