JUMP TO TOPIC

The concept of how to find the radius of convergence is the heart of power series in calculus, which one cannot overlook. Acting as the boundary between convergence and divergence, the radius of convergence breathes life into power series by defining the set of x-values for which the series converges.
Whether you’re a student grappling with the foundations of calculus or an expert seeking to brush up on your knowledge, understanding how to find the radius of convergence is critical.
In the following article, we will demystify the process of finding this elusive yet essential mathematical parameter. From its theoretical underpinnings to the nitty-gritty of calculations, we’ll explore a variety of approaches to efficiently and accurately find the radius of convergence for a given power series.
How to Find the Radius of Convergence
To find the radius of convergence, apply the Ratio Test: Determine the limit of the absolute value of the ratio of consecutive coefficients as the term number approaches infinity. If the limit exists, that value is the radius of convergence.
The radius of convergence of a power series ∑aₙ(x – c)ⁿ (from n = 0 to infinity) is the value r such that the series converges for all x for which |x – c| < r, and diverges for all x for which |x – c| > r.
In simple terms, it’s the distance from the center ‘c‘ of the power series to the endpoints of the interval of convergence. Below in figure-1, we present a generic power series and its radius of convergence.
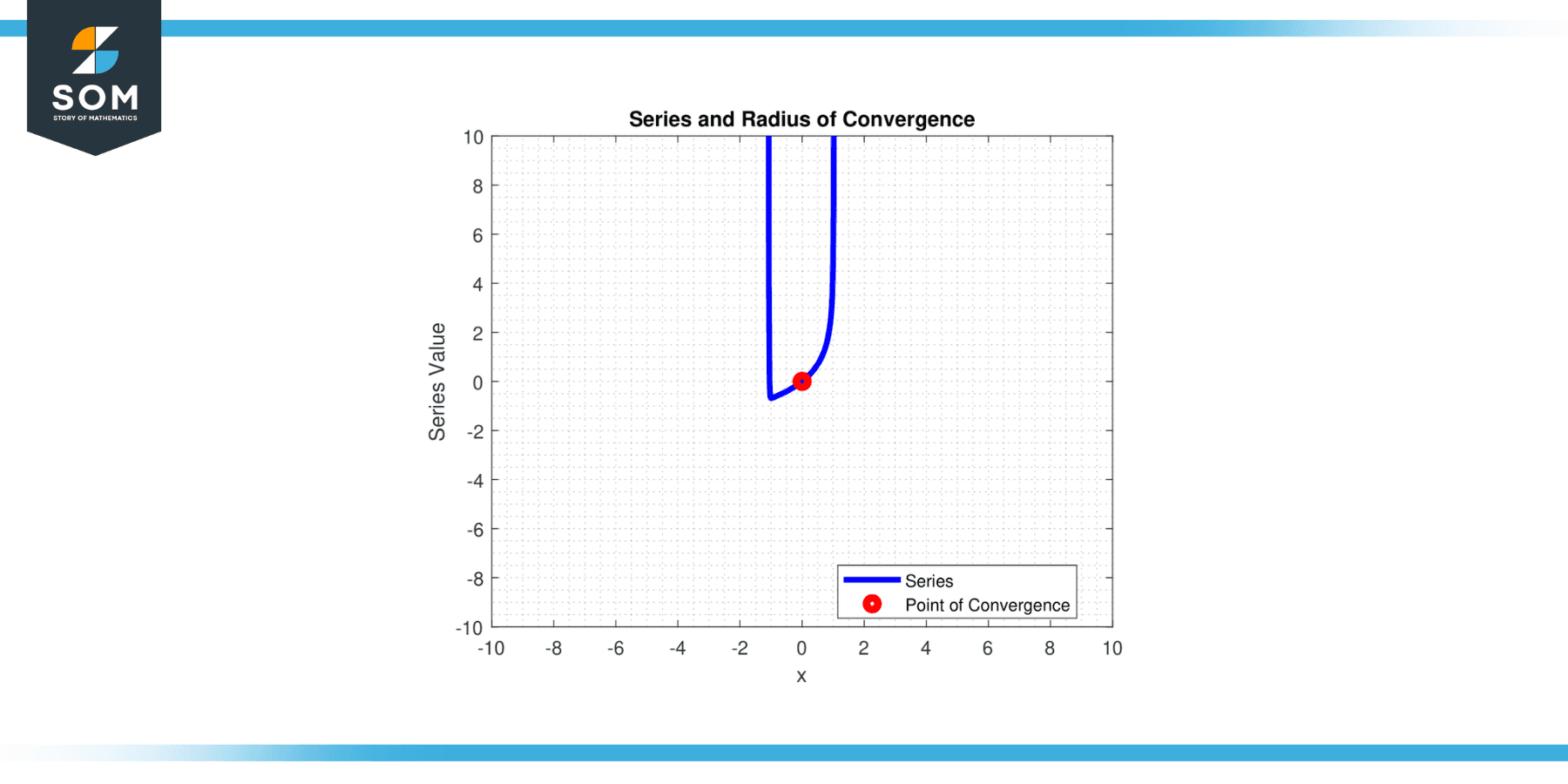
Figure-1.
Techniques of How to Find the Radius of Convergence
Ratio Test Method
This is the most commonly used method to find the radius of convergence.
For the given power series, take the ratio of the (n+1)th term to the nth term in absolute values, take the limit as n approaches infinity, and set this limit to be less than 1. This gives you the interval of convergence.
The ratio test states that for a series ∑aₙ, if we have L = lim (n→∞) |aₙ₊₁/aₙ|, the series converges absolutely if L < 1.
For the power series, this will yield an inequality of the form |x – c| < r, where r is the radius of convergence.
Root Test Method
Another method to find the radius of convergence uses the root test, which is particularly useful when the terms of the series have nth roots or powers of n.
For the given power series, take the nth root of the absolute value of the nth term, take the limit as n approaches infinity, and set this limit to be less than 1.
The root test states that for a series ∑aₙ, if we have L = lim (n→∞) |aₙ|⁽¹/ⁿ⁾, the series converges absolutely if L < 1.
For the power series, this will also yield an inequality of the form |x – c| < r, where r is the radius of convergence.
Remember, these methods only give the radius of convergence. To fully determine the interval of convergence, you must also check whether the series converges at the endpoints x = c ± r by substituting these values into the series and applying one of the convergence tests.
Historical Significance
The concept of the radius of convergence is part of a larger mathematical field called complex analysis, which is an extension of calculus. The origins of this concept are tied to the development of complex analysis and the use of power series in the 18th and 19th centuries.
The use of power series dates back to the time of Newton and Leibniz in the late 17th century, with Newton using power series as a primary tool in his development of calculus. In these early days, however, the concept of a “radius of convergence” had not yet been established.
Instead, mathematicians were mainly concerned with whether a given power series converged or diverged for specific variable values.
It wasn’t until the 18th century that mathematicians established a complete theory of power series. Swiss mathematician Leonhard Euler was particularly influential, extensively using power series in his work. Although Euler did not explicitly define the radius of convergence, he implicitly used the concept in his manipulations of power series.
The term “radius of convergence” and the rigorous theory surrounding it came about in the 19th century as mathematicians began to formulate the field of complex analysis. French mathematician Augustin-Louis Cauchy, one of the key figures in the development of complex analysis, provided much of the groundwork.
Cauchy was the first to prove that a power series converges absolutely within its circle (or “disk”) of convergence, which directly relates to the concept of the radius of convergence.
Karl Weierstrass, a German mathematician, later provided a more general and rigorous formulation of the limit processes involved, including the formulation of the root test, which can be used to find the radius of convergence of a power series.
Today, the concept of the radius of convergence is a standard part of any course in complex analysis or advanced calculus, and it plays a crucial role in many areas of mathematics, physics, and engineering.
Properties
The radius of convergence is closely tied to the properties of power series, a fundamental type of series in calculus and analysis. Here are some key properties that pertain to finding the radius of convergence:
Uniqueness
For a given power series, there is exactly one radius of convergence. The series will converge for all x within this radius about the center c and will diverge for all x outside it.
Dependence on Terms of Series
The radius of convergence is determined by the coefficients of the series, i.e., the terms aₙ. It does not depend on the center c of the series.
Determining Convergence
The radius of convergence determines an interval around the center of the series (c – r, c + r) where the series converges. However, it does not give information about the c – r and c + r endpoints. The series may converge or diverge, or one endpoint may behave differently than the other at these points. Each endpoint needs to be checked separately.
Role in Analytic Functions
The radius of convergence of a power series defines the domain over which the function represented by the series is analytic. Within this interval, the function has a power series representation that converges to the function.
Relation to Ratio or Root Test
The radius of convergence can be found using the ratio test or the root test. In general, if L = lim (n→∞) |aₙ₊₁/aₙ| or L = lim (n→∞) |aₙ|⁽¹/ⁿ⁾, the radius of convergence r is given by 1/L. If L = 0, the radius of convergence is ∞ (the series converges for all x); if L = ∞, the radius of convergence is 0 (the series only converges at the center point x = c).
Handling of Zero Radius
If the radius of convergence is zero, the series only converges at the center x = c.
Handling of Infinite Radius
If the radius of convergence is infinite, the series converges for all real numbers.
Algebraic Operations
If two power series both have a positive radius of convergence, you can add them together, subtract one from the other, multiply them, or divide one by the other to form a new power series. The new series will also have a positive radius of convergence, although determining the exact value requires additional work.
Applications
The concept of the radius of convergence is integral to many areas of mathematics and its applications in diverse fields such as physics, engineering, computer science, and economics. Some notable applications include:
Complex Analysis
In complex analysis, the radius of convergence is fundamental in defining and working with power series representations of complex functions. For instance, when defining a function as a power series in complex variables, the radius of convergence helps specify the region of the complex plane in which the power series is valid.
Differential Equations
The radius of convergence is crucial when using power series solutions for differential equations. The interval determined by the radius of convergence is the domain on which the solution is valid.
Physics
In physics, the radius of convergence is used in quantum mechanics and electrodynamics when calculating approximations for various quantities using perturbation theory. It’s also used in statistical mechanics when dealing with partition functions and thermodynamic potentials.
Engineering
In signal processing and control systems engineering, the radius of convergence is used when applying the Z-transform in discrete-time systems and the Laplace transform in continuous-time systems.
Computer Science
In algorithms and numerical analysis, the radius of convergence can influence the choice of methods for numerical approximation, as it can indicate how well a power series will approximate a function over a particular interval.
Economics
In economics, the concept of convergence is often used in the context of infinite series to model various economic phenomena, and understanding the radius of convergence is critical to ensure the validity of these models.
Probability Theory
In probability theory, generating functions are often used to solve complex problems. These are power series, and understanding their radius of convergence is crucial to determining the domain over which these functions are useful.
Exercise
Example 1
Consider the power series ∑nⁿ * xⁿ for n from 0 to infinity. Determine for which values of ‘x’ this series will converge. In other words, find the radius of convergence of this power series.
Solution
Apply the Ratio Test:
L = lim (n→∞) |(n+1)⁽ⁿ⁺¹⁾ x⁽ⁿ⁺¹⁾ / nⁿ xⁿ|
L = lim (n→∞) |(n+1) x|
L = |x| lim (n→∞) (n+1)
L = ∞ for all x ≠ 0
So, the series only converges for x = 0, and the radius of convergence r = 0.
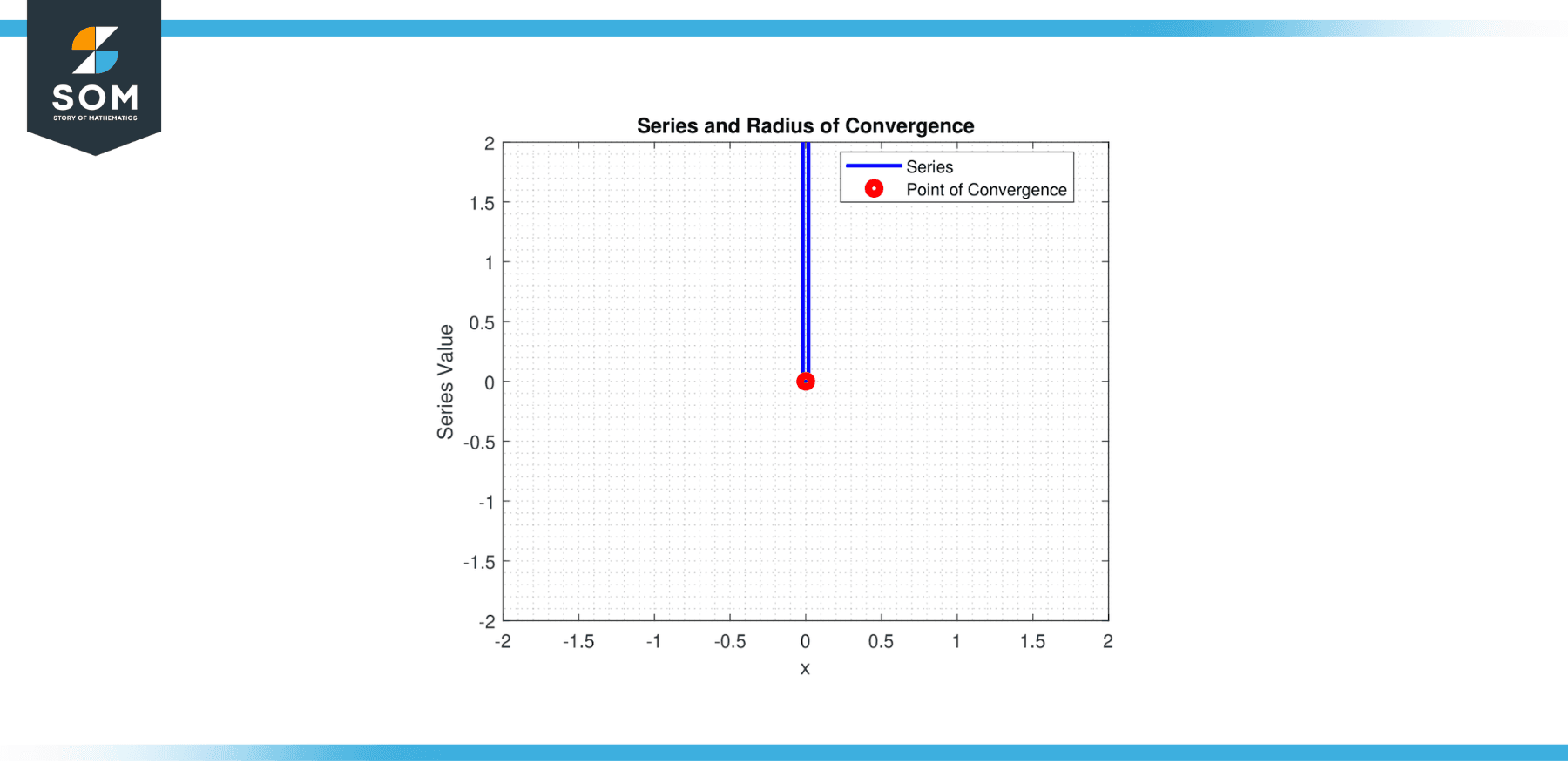
Figure-2.
Example 2
Consider the power series ∑xⁿ/n! for n from 0 to infinity frequently appears in mathematical analyses. We want to know for which real numbers ‘x’ this series converges. Can you determine the radius of convergence of this series?
Apply the Ratio Test:
L = lim (n→∞) |x⁽ⁿ⁺¹⁾/(n+1)! xⁿ/n!|
L = lim (n→∞) |x/(n+1)|
L = 0 for all x.
So, the series converges for all x, and the radius of convergence r = ∞.
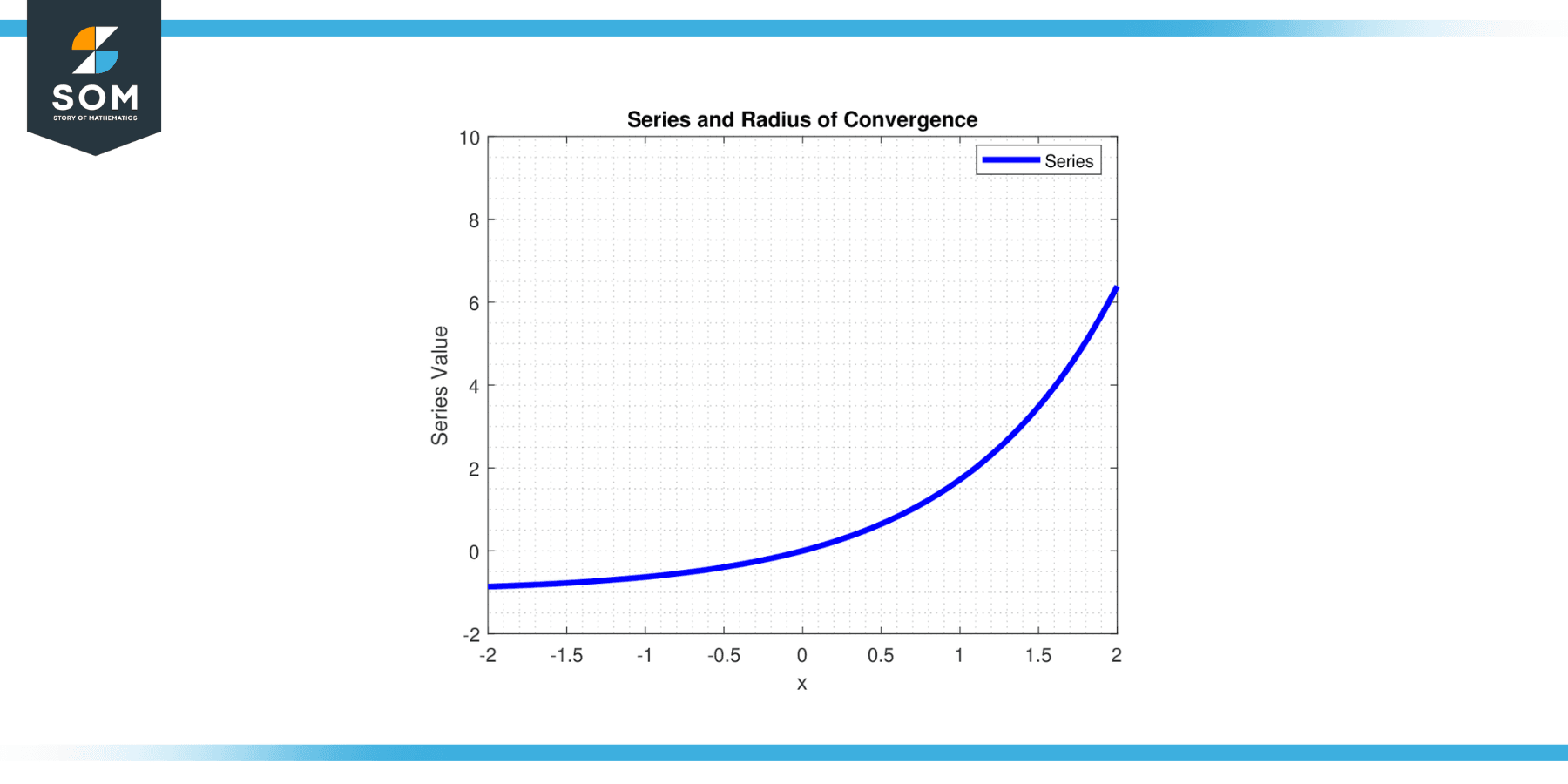
Figure-3.
Solution
Example 3
We have a power series ∑(n!*xⁿ) for n from 0 to infinity. This series has a specific range of ‘x’ values for which it converges. Task is to find the radius of convergence, i.e., the range of ‘x’ values where this series converges.
Solution
Apply the Ratio Test:
L = lim (n→∞) |(n+1)! x⁽ⁿ⁺¹⁾ / n! xⁿ|
L = lim (n→∞) |(n+1) x|
L = ∞ for all x ≠ 0
So, the series only converges for x = 0, and the radius of convergence r = 0.
Example 4
Given a power series ∑(xⁿ) / n² for n from 1 to infinity, we want to discover the ‘x’ values for which this series converges. Determine the radius of convergence for this series.
Solution
Apply the Ratio Test:
L = lim (n→∞) |x⁽ⁿ⁺¹⁾/(n+1)² xⁿ/n²| =
L |x| lim (n→∞) (n^2/(n+1)^2)
L = |x|
The series converges for |x| < 1, so the radius of convergence r = 1.
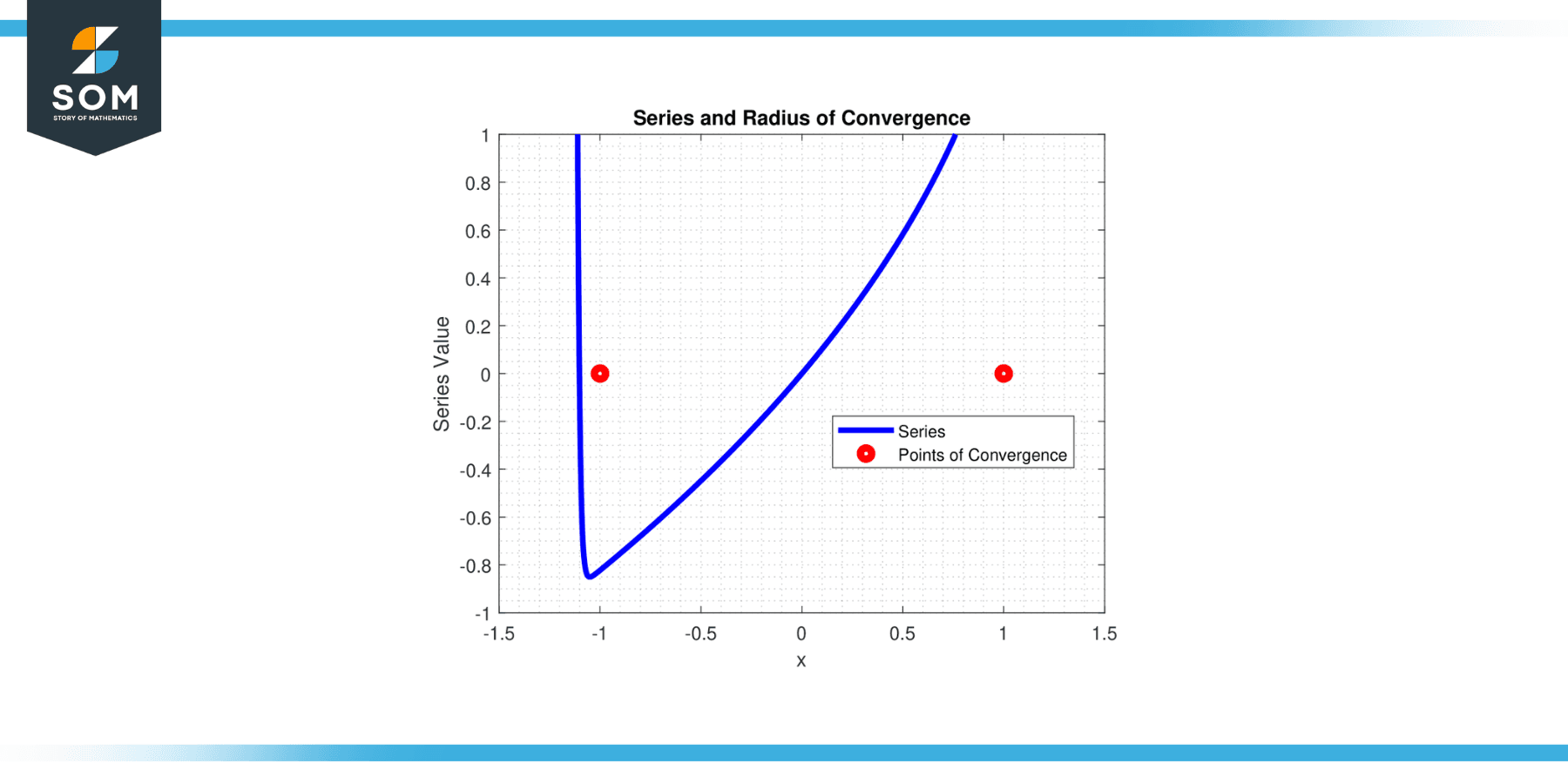
Figure-4.
Example 5
Look at the power series ∑((2ⁿ) * xⁿ) / n for n from 1 to infinity. We want to identify the values of ‘x’ for which this series converges. Calculate the radius of convergence of this series?
Solution
Apply the Ratio Test:
L = lim (n→∞) |((2⁽ⁿ⁺¹⁾x⁽ⁿ⁺¹⁾)/(n+1)) * (n/(2ⁿ xⁿ))|
L = 2|x| lim (n→∞) (n/(n+1))
L = 2|x|
The series converges for |x| < 1/2, so the radius of convergence r = 1/2.
Example 6
Examine the power series ∑xⁿ / 2ⁿ for n from 0 to infinity. We aim to find the ‘x’ values for which this series converges. Figure out the radius of convergence for this series?
Solution
Apply the Ratio Test:
L = lim (n→∞) |x⁽ⁿ⁺¹⁾/(2⁽ⁿ⁺¹⁾) xⁿ/2ⁿ|
L = |x/2|
The series converges for |x/2| < 1, so the radius of convergence r = 2.
Example 7
Consider the power series ∑(n²) * xⁿ for n from 0 to infinity. We are interested in the values of ‘x’ for which this series converges. Find the radius of convergence of this power series.
Solution
Apply the Ratio Test:
L = lim (n→∞) |((n+1)² x⁽ⁿ⁺¹⁾) / n² xⁿ|
L = |x| lim (n→∞) ((n+1)² / n²)
L = |x|
The series converges for |x| < 1, so the radius of convergence r = 1.
Example 8
Given the power series ∑(((-1)ⁿ) * xⁿ) / √n for n from 1 to infinity, we want to find out the ‘x’ values for which this series converges. Determine the radius of convergence of this series?
Solution
Apply the Ratio Test:
L = lim (n→∞) |((-1)⁽ⁿ⁺¹⁾ x⁽ⁿ⁺¹⁾) / √(n+1) * √n / ((-1)ⁿ xⁿ)|
L = |x| lim (n→∞) (√n / √(n+1))
L = |x|
The series converges for |x| < 1, so the radius of convergence r = 1.
All images were created with MATLAB.
