JUMP TO TOPIC
 Yes, the number $-6$ is a rational number because we can write it in $\dfrac{p}{q}$ form.
Yes, the number $-6$ is a rational number because we can write it in $\dfrac{p}{q}$ form.
To answer the question “Is -6 a rational number?” we should first learn what is meant by $\dfrac{p}{q}$ form. How can we write “$-6$” in $\dfrac{p}{q}$ form, and what p and q in this fraction mean? In this complete guide, we will study in detail why $-6$ is deemed as a rational number and how we can determine that $-6$ satisfies the criteria to be a rational number.
After covering this topic, you will know in detail why $-6$ is a rational number; furthermore, you will have the tools to identify whether any number is rational or not.
Is -6 a Rational Number?
Yes, the number $-6$ is rational because we can write it in $\dfrac{p}{q}$ form. But what does $\dfrac{p}{q}$ fraction mean? What is the acceptable value of “$p$” and “$q$” or what types of numbers are “$p$” and “$q$”? To answer this question correctly, we must be familiar with what a number is, its type and the types of rational numbers.
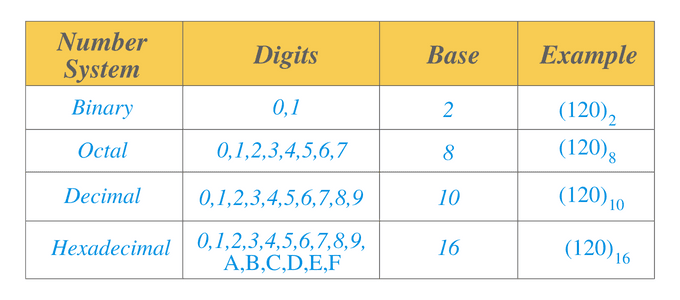
Number Systems
A number is a value used to determine the count of any object, or we can use it as a measurement tool or gauge for different things. The number can be a single digit or a combination of digits. For example, the number $6$ is also the digit $6$, but the number $66$ is a combination of two digits, i.e., $6$ and $6$. We can represent a number in many different ways. Let’s have a look at some famous number representations.
Let us list different types of the number system below:
- Binary number system
- Octal number system
- Decimal number system
- Hexadecimal number system
Binary Number System: A binary number system is a number system which has a base of 2. We can represent the numerical values in the binary number system in the form of 1s and 0s. For example, $0101$ is a binary number.
Octal Number System: An octal number system is a number system which has a base of 8. This system includes digits from $0$ to $7$. This number system, along with the binary number systems, is mainly used in electronics and computer applications. For example, $14_{8}$ is an octal number, and we can write it as $001100_{2}$ in a binary number system.
Decimal Number System: A decimal number system is a number system which has a base of $10$. This system includes digits from $0$ to $9$. If we go from the far right position and continue to the left, then the decimal position shows or represents a unit, tens, hundred, thousand, ten thousand, lacs and so on. This number system is used in mathematics. For example, for the number $110_{10}$, $0$ is the unit digit, the next digit “$1$” is the tenth digit, and the next “$1$” is the hundred digit.
Hexadecimal Number System: A hexadecimal number system is a number system which has a base of $16$. Just like the decimal number system, the first 10 digits are from 0 to 9. The next six numbers are written from “A” to “F”. $” A” $ will be represented by the decimal number “$10$” while F by the decimal number $16$.
Types of Numbers
Now that we have seen some possible representations of a number, let’s discuss some basic types of numbers used in mathematics.
Natural Numbers: Natural numbers are the standard numbers we use in counting, i.e., $1$,$2$,$3$ and $4$.
Whole Numbers: We can write the whole numbers in the form $0$,$1$,$2$,$3$,$4$,$5$ etc. So they are like natural numbers, but they also include the number “$0$,” which is not included in natural numbers.
Integers: The set of integers contains all the natural numbers, $0$, as well as negative counterparts of all the natural numbers. The set of integers is usually denoted by $Z$, i.e., $Z = \{\cdots,-3,-2,-1,0,1,2,3,\cdots \}$.
Rational Numbers: Rational numbers are those numbers that can be written as $\frac{p}{q}$, where both $p$ and $q$ are integers, and $q$ is not equal to zero. Examples of rational numbers are $\frac{22}{7}$, $3.14 = \frac{314}{100}$, etc. Note that all integers are rational numbers because we can write $-4$, $-2$ etc., as $\frac{-4}{1}$, $\frac{-2}{1}$. Now, $-6$ is also an integer; we can write it as $\frac{-6}{1}$ and hence it is a rational number.
Irrational Numbers: The numbers that we cannot write in $\frac{p}{q}$ are irrational numbers. Some important examples include the square root of 2, $\pi$ etc.
Real Numbers: Real numbers can be said to be the superset of numbers as they include integers, natural numbers, whole numbers, and irrational and rational numbers. The only number which is not included in the real numbers is the complex numbers.
We can write real numbers in any form other than an imaginary number, so we can say that all mathematics operations which does not involve complex numbers will use real numbers. For example, $\dfrac{1}{4}$, $0.33134$, $\pi$ all are real numbers.

Complex Numbers: The numbers which can be written in $x+iy$ form are known as complex numbers. Here, “$i$” is known as iota, and iota is equal to $\sqrt{-1}$ while “$x$” and “$y$” are real numbers. Any number which includes “iota” will be termed a complex number. For example, the number $4+6i$ is a complex number. Here, $4$ is the real part, and $6$ is the imaginary part.
Now that you have learned about different types of numbers and their properties, it will be much easier to understand the types of rational numbers. Let us now discuss which numbers are subsets of rational numbers.
Types of Rational Numbers
We can classify the rational numbers into different types, and some of them are given below.
- Whole Numbers
- Integers
- Terminating Decimal numbers
- Repeating decimal numbers
Whole Numbers: All the whole numbers can be represented as $\dfrac{p}{q}$ form. So we can say that all whole numbers are rational numbers. For example, the number $0$ can be written in $\dfrac{p}{q}$ from $\dfrac{0}{1}$. Similarly, we can write the number “$1$” as $\dfrac{1}{1}$.
Integers: Integers are a subset of rational numbers, so all the integers can be represented in $\dfrac{p}{q}$ form. For example, the number $1$,$-2$,$-3$ can be written as $\dfrac{1}{1}$, $\dfrac{-2}{1}$,$\dfrac{-3}{1}$ etc.
Terminating Decimal Numbers: The decimal numbers with limited numbers after the decimal point are known as terminating decimal numbers. For example, $0.86$, $0.987$, and $0.8776456$ are all terminating decimal numbers, and all such numbers are rational numbers as they can be written in $\dfrac{p}{q}$ form.
Repeating Decimal Numbers: The decimal numbers in which the number(s) after the decimal point repeat itself are known as repeating decimal numbers. For example, $0.33333$, $0.666666$ and $0.656656656$ are all repeating decimal numbers. All the repeating decimals are rational numbers.
Identification of Rational Numbers
A number will be called a rational number if:
- It can be written in the $\dfrac{p}{q}$ form, whereas p and q are integers and q is not zero.
- A number is given in the decimal form and its fraction part (the part after the decimal point) contains either a finite number of digits or a repeating pattern of digits, then it is a rational number.
Let us study similar examples to the number -6 and see which numbers are rational numbers.
Example 1: Is negative 8 a rational number?
Answer
Yes, as it can be written in \dfrac{p}{q} form.
Example 2: Is 0 a rational number?
Answer
Yes, as it can be written in \dfrac{p}{q} form.
Example 3: Is pi a rational number?
No, it is irrational and cannot be represented in \dfrac{p}{q} form.
Example 4: Is 2 a rational number?
Answer
Yes.
Example 5: Is negative 3 a rational number?
Answer
Yes.
Example 6: Is 4 a rational number?
Answer
Yes.
Frequently Asked Question
Is 3.14 a Rational Number?
Yes, 3.14 is a rational number. This is a tricky question since some students confuse $3.14$ with the value of $\pi$, which is $3.14159265359\cdots$. Note that $\pi$ is a non-repeating and non-terminating decimal number and hence is irrational. $3.14$, on the other hand, is a terminating decimal number; hence it is a rational number.
Remember that $3.14$ is sometimes used as an approximation to $\pi$ but it is not equal to $\pi$.
Conclusion
Let us conclude what we have learned so far in the bullets given below.
- The number negative 6 can be written in p/q form, hence it is a rational number.
- Any number that can be written in p/q, provided that q is not equal to zero, will be a rational number.
- Not only negative 6, but all negative and positive integers can be written in p/q and hence are rational numbers.
