JUMP TO TOPIC
 Yes, the number $-1$ is a rational number because we can write the number negative $1$ in $\dfrac{p}{q}$ form.
Yes, the number $-1$ is a rational number because we can write the number negative $1$ in $\dfrac{p}{q}$ form.
So, the question arises, “what is meant by $\dfrac{p}{q}$ form?” “What is meant by “p” and what is meant by “$q$”?” In this article, we will study in detail what makes “$-1$” a rational number and, more importantly, how we determine which number is a rational number.
At the end of this topic, you will have a firm grip on the concept of rational numbers, and you will easily differentiate between a rational and an irrational number.
Is -1 a Rational Number?
Yes, the number “$-1$” is a rational number because it is an integer, and all integers are rational numbers. Hence, the number “$-1$” can be written as $-\dfrac{1}{1}$, so we can say that “$-1$” is a rational number.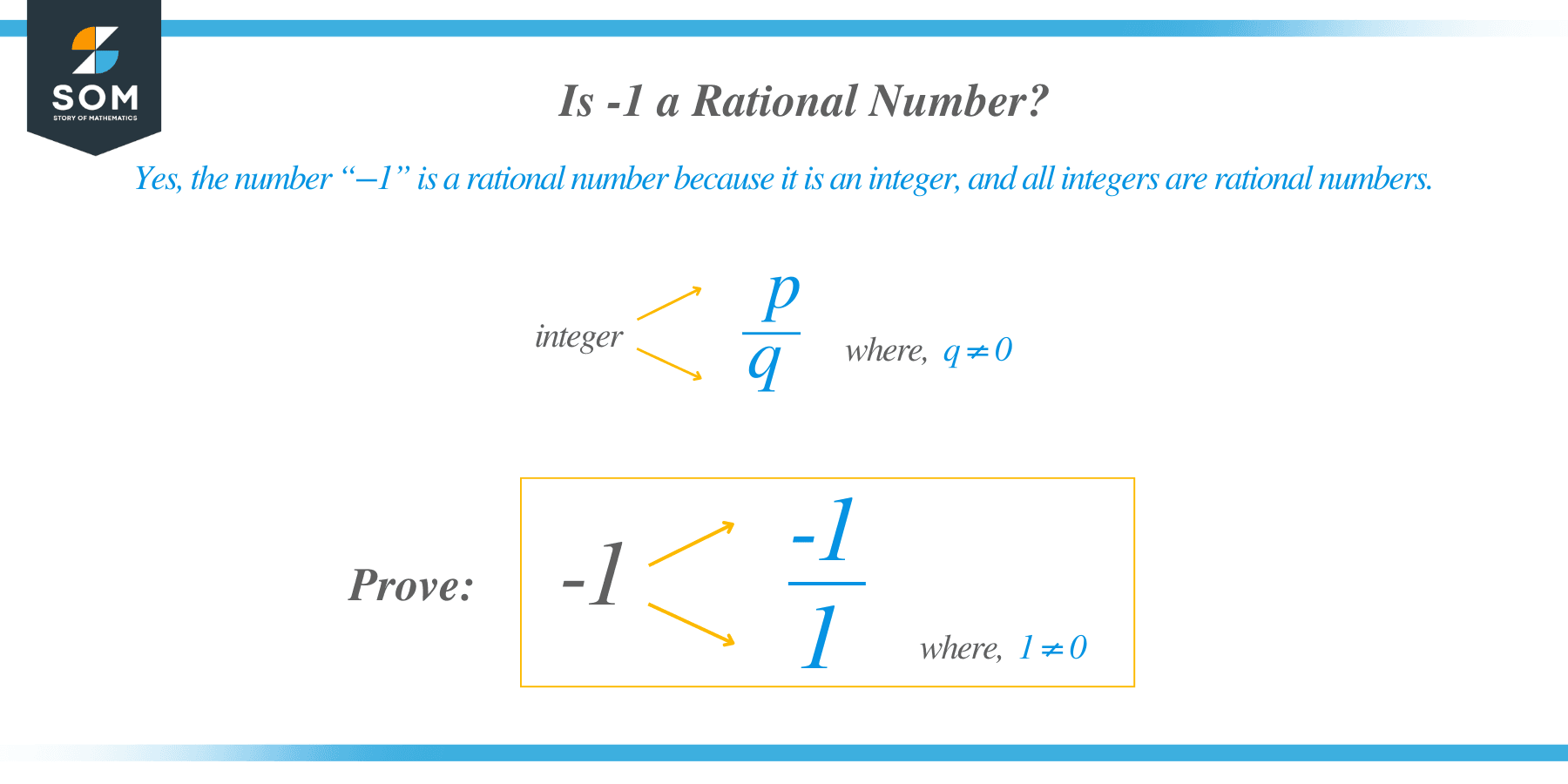
Let us cover some examples, so that concept of rational numbers becomes crystal clear for you.
Example 1: Is the number $-1.1111$ rational number?
Solution:
Yes, the number $-1.1111$ is rational number as it can be written in $\dfrac{p}{q}$ form as $-\dfrac{11111}{10000}$.
Example 2: Is the number $1$ $\dfrac{1}{1}$ a rational number?
Solution:
Yes, the number $1$ $\dfrac{1}{1}$ is a rational number as it can be written as $\dfrac{2}{1}$ which is a fraction; hence it is a rational number.
Example 2: Is negative 2 a rational number?
Solution:
Yes, it is a rational number.
Example 2: Is negative 12 a rational number?
Solution:
Yes, it is a rational number.
Example 2: Is negative 3 a rational number?
Solution:
Yes, it is a rational number.
Rational Numbers
The word rational is derived from the Latin word “ratio,” which in Latin means reasonable, calculate-able or having a ratio. The ratio is a comparison between 2 or more numbers given in fraction form, so we can extract that rational numbers will always be given in fraction form.
In short, the numbers which can be expressed in $\dfrac{p}{q}$ or fraction form are called rational numbers. The rational number can be a negative, positive or zero number. The only thing that should be kept in mind is that for the expression $\dfrac{p}{q}$, the value of “$q$” should be $\neq$ 0 otherwise, it will give us an indefinite answer which is not acceptable in maths.
For example, the number $\dfrac{5}{3}$ is considered to be a rational number where the integer $5$ is divided by an integer $3$ and as the value of “$q$” is not zero, hence it is a rational number.
What Is a Number?
Numbers are used as a measurement tool in mathematics, and they are the symbols to represent the count of a thing or subject. We know numbers can be a single digit or two or more digits. To learn how to identify a rational number, it is essential that we first cover the basics related to a number itself and its types and know the difference between a number and a digit.
Numbers vs Digits
A digit is a numerical representation of the following symbols $0,1,2,3,4,5,6,7,8$, and $9$. So all these numerical symbols are known as digits, and when we combine two or more digits together, it will give us a number. So a digit is a single numeral representation of a count or number, while a number is a numeral representation having one or more than one digits. For example, if Anna has $25$ books in her library, then $25$ is a number while “$2$” and “$5$” are digits.
Now that we know the difference between a number and a digit, let us discuss different types of numbers and their properties. There are different types of numbers, and some of them are given below.
- Binary numbers
- Natural numbers
- Whole numbers
- Integers
- Rational numbers
- Irrational numbers
- Real Numbers
- Complex numbers
Binary Numbers: In mathematics, if the numbers are only represented by 1’s and 0’s, then we call them binary numbers. This means every numerical number will be represented in the form of 1’s and 0’s. For example, “0” is represented as “$0$” in binary and similar the number “$1$” is represented as “$1$” while the number $2$ will be represented as 10 while the number $3$ is represented as $011$ and so on.
Natural Numbers: In mathematics, all the positive integers are known as natural numbers. Natural numbers start from the number $1$ up to infinity, but these are all positive numbers.
Whole Numbers: The whole numbers are basically a set of natural numbers but they also include the number “$0$” in addition to all natural numbers. So the whole numbers start from the number zero up to infinity. We can write whole numbers as $0,1,2,4$,…..
Integers: Integers consists of all the whole numbers as well as there negative counterparts, i.e., $\cdots, -4,-3,-2,-1,0,1,2,3,4,\cdots$.
Rational Numbers: The numbers which can be written as $\dfrac{p}{q}$, where both $p$ and $q$ are integers and $q\neq 0$ are called rational numbers. All natural numbers, whole numbers, and integers themselves are rational numbers. For example, we can write $-4$ as $\dfrac{-4}{1}$ and hence it is a rational number. Also, $\dfrac{5}{7}$, $\dfrac{2}{3}$ and $\dfrac{1}{8}$, etc., are examples of rational numbers.
Irrational Numbers: The number which cannot be expressed in $\dfrac{p}{q}$ form or the number which cannot be expressed in fraction/ratio form is known as an irrational number. Mathematicians initially perceived that all the numbers were rational and could be written in $\dfrac{p}{q}$ form, but later on, Greeks discovered that some roots of equations cannot be written in a fraction form, so they termed them as irrational numbers. Common irrational numbers are $\sqrt{2}$, $\pi$ etc.
Real Numbers: Real numbers consist of both rational and irrational numbers. For example, $\dfrac{1}{2}$, $0.3333$, and $\pi$ all are real numbers.
Complex Numbers: The numbers which are expressed or written in a+ix form are termed complex numbers. Here, “$a$” and “$b$” both are real numbers, while the “i” is called iota and is an imaginary number and is equal to $\sqrt{-1}$. So any real number which is written along iota will be termed an imaginary number. For example, if we are given a number “$3+4i$,” then “$3$” is called the real number while $4$ is called the imaginary number, and as a whole “$3+4i$” is called a complex number.
Types of different numbers and their definition were necessary because some of them are also types of rational numbers. Now let’s have a look at the various types of rational numbers.
Types of Rational Numbers
Rational numbers can be classified into different types, and some of them are given below.
- Whole Numbers
- Natural Numbers
- Decimal Numbers
- Fractions
Whole Numbers: The whole numbers can be written in $\dfrac{p}{q}$ form; hence all the whole numbers are rational numbers, including the number “$0$”. For example we can write $0$ as $\dfrac{0}{1}$,$\dfrac{0}{2}$,$\dfrac{0}{3}$,$\dfrac{0}{4}$ and so on
Natural Numbers: Like whole numbers, all the natural numbers are also rational numbers as they can also be expressed in $\dfrac{p}{q}$ form. For example, $\dfrac{2}{1}$, $\dfrac{3}{1}$,$\dfrac{4}{1}$ etc
Decimal Numbers: The numbers divided into two parts which are separated by a point “.” are known as decimal numbers. The number(s) on the left side of the point are whole numbers, while the numbers on the right-hand side of the point are known as fractions. For example, the number $18.36$ is known as a decimal number where 18 is the whole number while $36$ is the decimal part or fraction part of the number.
Some of the decimal numbers are also rational numbers. There are different types of decimal numbers, for example, terminating decimal numbers, repeating decimal numbers, and non-terminating decimal numbers.
All the terminating decimals are rational numbers as they can be written in $\dfrac{p}{q}$ form; for example, $0.64$, $0.75$, and $0.67124$ all these numbers are rational numbers
All the repeating decimals are also rational numbers. Repeating decimals are the numbers where the decimal part of the number repeats itself. For example, numbers 2.1111111 and $3.121212$ are rational numbers.
Finally, the non-terminating and non-repeating decimals are not rational numbers. For example, the decimal notation of $\pi$ is $3.14159\cdots$. Note that it is a non-terminating decimal number that does not repeat itself.
Integer Numbers: All integers are rational numbers as well.
How to Identify Rational Numbers
There are certain tricks to easily identify a rational number, and they are:
1. If the number is written in $\dfrac{p}{q}$ form such that $p$ and $q$ are integers and $q$ $\neq$ $0$, then the number is a rational number.
2. If the number is not given in fraction form but we are given a number in decimals instead, then we will check whether the fraction part is terminating or repeating. In both cases, it will be a rational number.
3. All real numbers are rational numbers, excluding those which cannot be expressed as $\dfrac{p}{q}$ form.
After learning all about numbers and how to identify rational numbers, we can develop a Venn diagram for rational and irrational numbers, which is given below.

The diagram for irrational numbers does not include any subset, and it can be drawn as:

Practice Questions:
- Is number $-\dfrac{1}{0}$ a rational number?
- Is 0 a rational number?
- Is number $\sqrt{1}$ a rational number?
- Is number $\sqrt{-1}$ a rational number?
- Is 1/2 a rational number?
- -3 is a rational number, true or false.
Answer Key:
1)
No, the number $-\dfrac{1}{0}$ is not a rational number because the value of “q” in this case is zero; hence the number is not defined, and it is not a rational number.
2)
Yes, 0 is a rational number.
3)
Yes, $\sqrt{1}$ is rational a rational number as $\sqrt{1} = 1$. Since “$1$” is a rational number, so $\sqrt{1}$ is also a rational number.
4)
No, $\sqrt{-1}$ is not a rational number. As all the rational numbers are real numbers while $\sqrt{-1}$ is an imaginary number, hence it is not a rational number.
5)
Yes, $\dfrac{1}{2}$ is a rational number.
6)
Yes, $-3$ is a rational number.
