Use the Distributive Property To Remove the Parentheses

We can use the distributive property to remove the parenthesis in a mathematical expression by properly distributing the multiplication operation inside the parenthesis. 

The process of eliminating the parentheses using the distributive property is essential in solving many mathematical problems. This guide will help you understand the concept of the distributive property and how we can use it to remove the parentheses.

What Is Distributive Property?

The distributive property is the property used to distribute or divide a whole quantity, numbers, or something calculable. According to this property, if we multiply the sum of two or more numbers by a specific number, then it will be equal to the summation of the two numbers, provided they are individually multiplied by the same specific number. We can represent the distributive property as:

$a (b\hspace{1mm} +\hspace{1mm} c) = ac \hspace{1mm}+ \hspace{1mm}bc$

So we can see if we multiply the summation of b&c with “a,” then it will be equal to the summation of “$ac$” and “$bc$.”

Let us discuss some real-life examples to understand the application of distributive property. Consider a cinema screen. The cinema room has two types of seats: a) Premium and b) Regular. The premium seats are in the blue section, while the regular seats are in the yellow section.

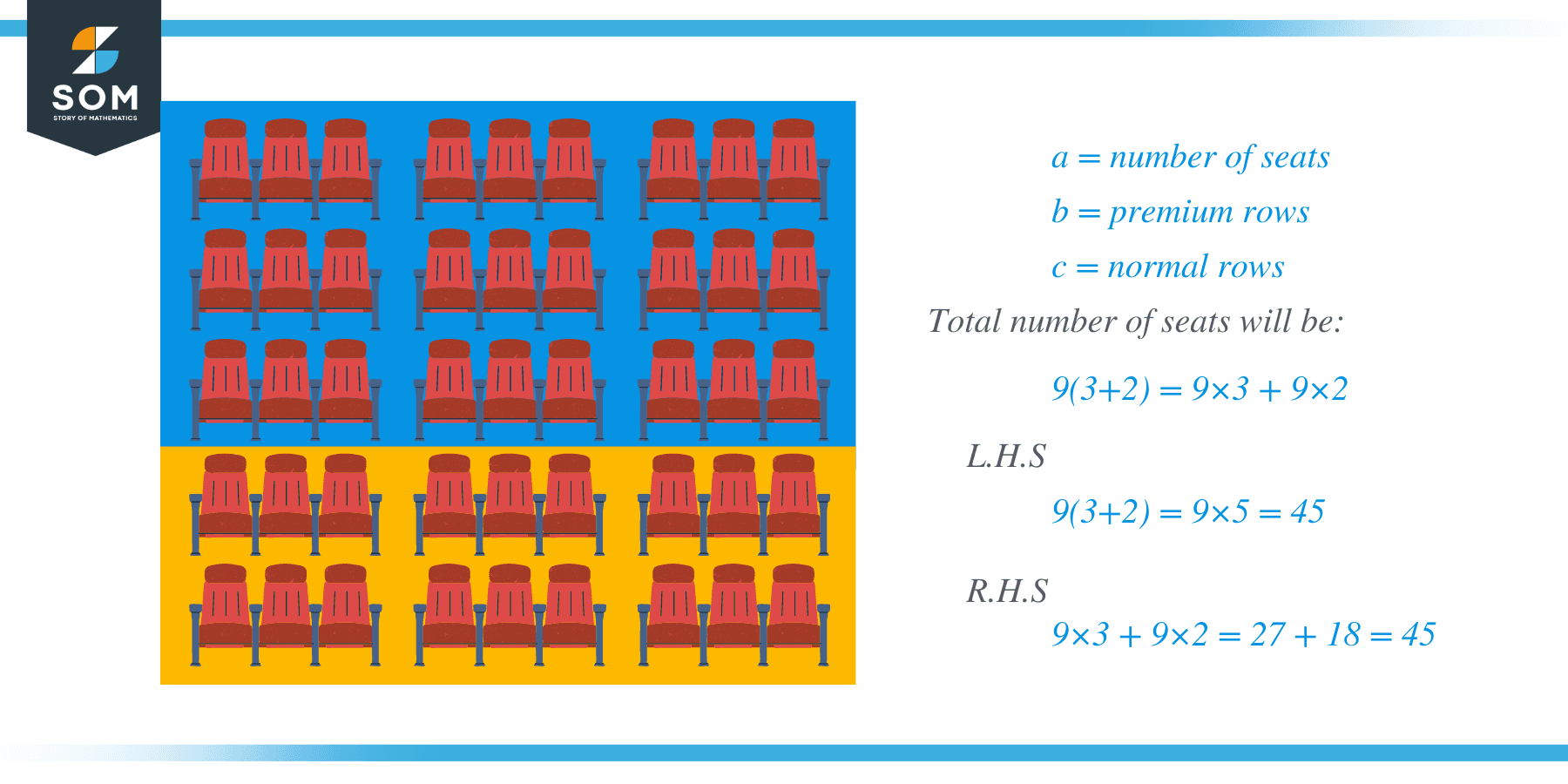
There are three rows for the premium seats, while the number of rows for the regular seats is only two. If each row contains nine seats, we can calculate the total number of seats using two methods.

We can multiply the number of rows with the total number of seats in a row separately for both enclosures, or we can just all the number of rows of the yellow enclosure with the rows in the blue enclosure and multiply them by the number of seats in a single row.

If

a = number of seats

b = premium rows

c = normal rows

Then total number of seats will be:

$9 (3\hspace{1mm} +\hspace{1mm} 2) = 9\times3 \hspace{1mm}+ \hspace{1mm}9\times 2$

We have removed the parentheses and multiplied the numbers of seats in a row separately with premium and normal rows.

L.H.S $= 9 (3 \hspace{1mm}+ \hspace{1mm}2) = 9 \times 5 = 45$

R.H.S $= 9\times3 \hspace{1mm}+ \hspace{1mm}9\times 2 = 27\hspace{1mm} +\hspace{1mm} 18 = 45$

Let us take another example and see how the results are the same when we solve the problem without using the distributive property and when the same problem is solved by removing the parentheses by using the distributive property.

There are two columns for blue squares and one number of columns for red squares. The number of rows for both blue and red squares equals four.

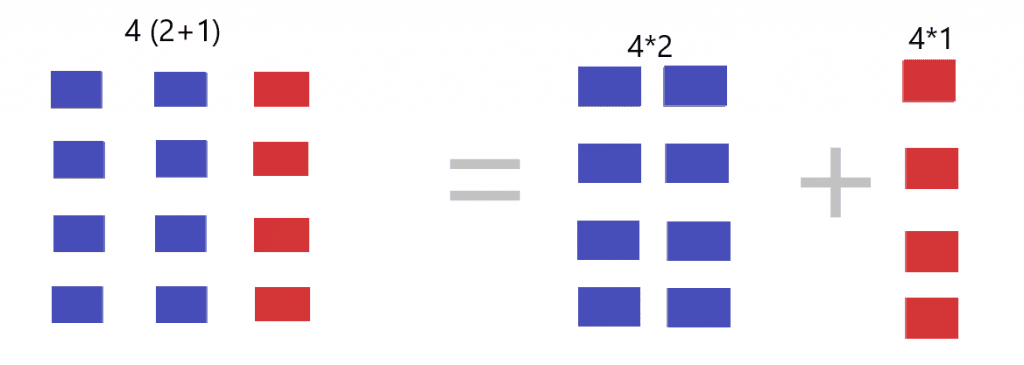
$4 (2 \hspace{1mm}+ \hspace{1mm}1) = 4\times2\hspace{1mm} +\hspace{1mm} 4\times 1$

L.H.S $= 4 (2 \hspace{1mm}+ \hspace{1mm}1) = 4 \times 3 = 12$

R.H.S $= 4\times2 \hspace{1mm}+ \hspace{1mm}4\times 1 = 8 \hspace{1mm}+ \hspace{1mm}4 = 12$

How To Use Distributive Property To Remove Parentheses

The distributive property helps us break down the given problem so we can solve it easily. The examples we studied in the previous sections are the distribution property of multiplication. We were given a problem, re-wrote or divided it into parts, and solved it.

We have seen that the expression $a (b \hspace{1mm} + \hspace{1mm}c)$ is equal to $ac + bc$. So we have divided the term $a (b + c)$ into a summation of “$ac$” and “$bc$”. We can also do that for more than one variable, for example, we can re-write the term $a (b \hspace{1mm} +\hspace{1mm} c \hspace{1mm}+ \hspace{1mm}d)$ as “$ab\hspace{1mm} + \hspace{1mm}ac \hspace{1mm}+\hspace{1mm} ad$”. This process of dividing the complete term into parts is called the expansion of the expression and whenever we expand the expression we have to remove the given parentheses.

We can use the distribution property of multiplication over addition or the distributive property of multiplication over subtraction to solve complex problems by dividing them into smaller parts. For example, you are given $4 \times 23$ and asked to solve using the distributive property. Now you can calculate this expression by writing $23$ as $(20 \hspace{1mm}+ \hspace{1mm}3)$ or $(26 \hspace{1mm} – \hspace{1mm}3)$.

If we solve the example as $4 (20 \hspace{1mm} + \hspace{1mm}3)$ = $4\times 20 \hspace{1mm}+ \hspace{1mm}4 \times 3 = 80 \hspace{1mm}+ \hspace{1mm}12 = 92$, this is called solving the expression by using distributive property of multiplication over addition.

If we solve the example as $4 (26 – 3) = 4\times 26 \hspace{1mm} – \hspace{1mm}4 \times 3 = 104 \hspace{1mm} – \hspace{1mm} 12 = 92$, this is called solving the expression by using the distributive property of multiplication over subtraction.

Example 1: Simplify $4 (a \hspace{1mm}+ \hspace{1mm}6)$ by using the distributive property.

Solution

We can simplify the above expression by using the distributive property of multiplication over addition.

$4 ( a \hspace{1mm}+\hspace{1mm} 6) = 4\times a \hspace{1mm}+ \hspace{1mm}4\times 6 = 4a + 24$

Example 2: Use the distributive property to simplify the expression $8 (a \hspace{1mm} – \hspace{1mm}2)$.

Solution

We can simplify the above expression by using the distributive property of multiplication over subtraction.

$8 ( a \hspace{1mm} – \hspace{1mm} 2) = 8\times a \hspace{1mm} – \hspace{1mm} 8\times 2 = 8a \hspace{1mm} – \hspace{1mm}16$

Example 3: Use the distributive property to remove parentheses of the expression $4 (3a + 5)$.

Solution

We can simplify the above expression by using the distributive property of multiplication over addition.

$4 (3a \hspace{1mm} +\hspace{1mm} 5) = 4\times 3a \hspace{1mm} + \hspace{1mm}4\times 5 = 12a\hspace{1mm} + \hspace{1mm} 20$

Example 4: Allan works as a waiter at three restaurants for a week. He is paid on a shift basis in each restaurant. The first restaurant pays him “$a$” dollars for a week of service. The second restaurant pays him “$b$” dollars, and the third restaurant pays him “$c$” dollars for doing a single shift. If Allan does two shifts at a third restaurant, simplify the expression by showing his total pay in $5$ weeks.

Solution

The expression for the total pay Allan gets can be written as $5 (a \hspace{1mm} + \hspace{1mm}b +\hspace{1mm} 2c)$. We can remove parentheses from expression to simplify the expression if we use the distributive property to rewrite each expression. So we can write the given expression as $5.a + 5.b + 5.c = 5a\hspace{1mm}+ \hspace{1mm}5b \hspace{1mm}+ \hspace{1mm}5c$ dollars.

Distributive Property and Fractions

We can also use the distributive law or property to expand an expression having fractions, or we can say that we can expand any division expression because we can convert any division expression into multiplication form, e.g., we can write $8 \div 4$ as $8 \times \dfrac{1}{4}$.

Suppose you are given an expression $(x + y)$ and if u divide it by “$c$” then you can write the expression as $\dfrac{x+y}{c}$. Dividing the expression by “$c$” is the same as multiplying the expression by “ $\dfrac{1}{c}$”. So by using the distributive property of multiplication over addition, we can write:

$\dfrac{1}{c}(x \hspace{1mm} + \hspace{1mm} y)$ as $\dfrac{1}{c}x + \dfrac{1}{c}y.$

Example 5: Simplify the expression $\dfrac{40 \hspace{1mm} +\hspace{1mm} 6x}{2}$ by using the distributive property.

Solution

$\dfrac{40 \hspace{1mm} + \hspace{1mm} 6x}{2} = \dfrac{40}{2} \hspace{1mm} + \hspace{1mm} \dfrac{6x}{2} = 20 \hspace{1mm} + \hspace{1mm}3x$

Frequently Asked Question

How Do I Use the Distributive Property?

To use the distributive property to solve a given expression, you need to multiply the number or the term given outside the parentheses with each number present inside the parentheses. For example, if the number 6 is outside the parentheses and the expression $(2 \hspace{1mm}+ \hspace{1mm}4)$ is inside the parentheses, then we will multiply $6$ with “$2$” and “$4$” separately.

The answer you get by solving the expression inside the parenthesis first and then multiplying by the value outside is the same as if you remove the parenthesis using the distributive property and solving the expression. Sometimes, removing the parenthesis can simplify the expression; hence, you should choose to remove the parenthesis if it helps you simplify the question.

Conclusion

Let us conclude our discussion with the important points listed below.

• We can use the distributive property to expand and solve complex expressions. It tells us how to remove parentheses in an equation.
• We can use the distributive property of multiplication over addition and subtraction to remove the parentheses depending on the type of expression given to us.
• We can also use the distributive property to expand the fraction expressions.

Understanding how to use the distributive property to remove the parentheses will be simple for you now that you have read our guide.