JUMP TO TOPIC
The vertex formula is used to solve for the vertex $(h,k)$ of a parabola. The vertex is the point in the parabola that describes the maximum or minimum value of the function. The vertex formula gives the exact vertex of a given quadratic equation without plotting the graph of the parabola.
Similarly, we can derive the equation of the parabola if we know the vertex of the graph and $a$. In this guide, we will discuss how to find the vertex of a parabola using the vertex formula, writing the vertex form of the equation of the parabola through examples with detailed solutions.
What Is the Vertex Formula?
The vertex formula helps solve the coordinates of the vertex $(h,k)$ of the parabola by giving an indicated formula for $h$ and $k$. The standard equation form of the parabola is given by
$$y=ax^2+bx+c.$$
Using the values of the coefficients of the quadratic equation, the vertex formula gives us the values of $h$ and $k$ as
$$h= \dfrac{b}{2a}$$
and
$$k=-\dfrac{b^2-4ac}{4a}.$$
Examples
Look at the following example of using the vertex formula in solving for the vertex of a parabola.
Example 1
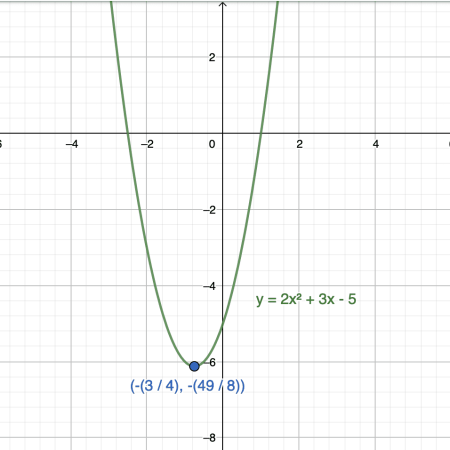
- Find the vertex of the parabola given by the equation $y=2x^2+3x-5$.
We take the coefficients $a=2$, $b=3$, and $c=-5$. We substitute these values in the vertex formula to find the vertex.
$$h=-\dfrac{3}{2(2)} =-\dfrac{3}{4}$$
and
$$k= -\dfrac{(3)^2-4(2)(-5)}{4(2)} =-\dfrac{9+40}{8}=-\dfrac{49}{8}.$$
Thus, the vertex of the parabola is at the point $\left(-\dfrac{3}{4},-\dfrac{49}{8}\right)$.
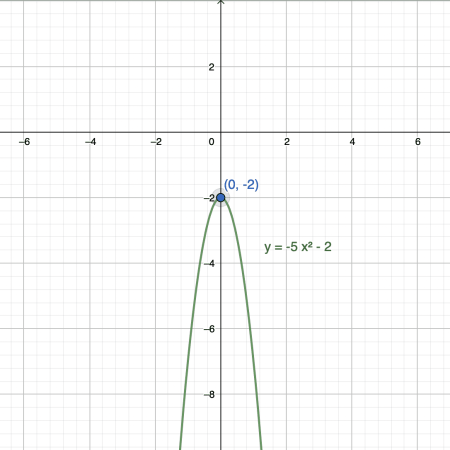
- Solve for the vertex of the parabola described by the equation $y=-5x^2-2$.
Note that since the equation has no middle term, $b=0$, and we have $a=-5$ and $c=-2$. Plugging in these values in the vertex formula gives us:
$$h=-\dfrac{0}{2(-5)} =0$$
and
$$k=-\dfrac{(0)^2-4(-5)(-2)}{4(-5)} =-\dfrac{-40}{-20}=-2.$$
Hence, the vertex of the parabola is the point $(0,-2)$.
The Vertex Form of a Parabola
The standard form of the equation of a parabola is given by:
$y=ax^2+bx+c.$
When $a$ is positive, the parabola opens upward, making the vertex the minimum of the function. When $a$ is negative, the parabola opens downward, and the vertex is the maximum point in the graph. The vertex is significant in graphing the curve of the parabola because it indicates the turning point of the parabola.
After finding the vertex $(h,k)$ using the vertex formula, we can rewrite the standard equation into a form where we can easily identify the vertex of the parabola. The vertex form of the parabola is given by:
$y=a(x-h)^2+k.$
Let’s transform the standard form of the parabola into the vertex form in the following example.
Example 2
- Find the vertex of the parabola $y=3x^2-4x+9$ and write the vertex form of the parabola.
The given parabola has coefficients $a=3$, $b=-4$, and $c=9$. Using the vertex formula, we solve for the coordinates of the vertex.
$$h=-\dfrac{-4}{2(3)} =-\dfrac{-4}{6}=\dfrac{2}{3}$$
and
$$k= -\dfrac{(-4)^2-4(3)(9)}{4(3)} =-\dfrac{16-108}{12}=\dfrac{92}{12}=\dfrac{23}{3}.$$
The vertex of the parabola is at the point $\left(\dfrac{2}{3},\dfrac{23}{3}\right)$. Using the coordinates of the vertex we obtained, we write the vertex form of the parabola as:
$$y=3\left(x-\dfrac{2}{3}\right)^2+\dfrac{23}{3}.$$
Let’s try to verify if the vertex form is correct. If we simplify the vertex form, we should still arrive at the standard form of the equation of the parabola.
\begin{align*}
y&=3\left(x-\dfrac{2}{3}\right)^2+\dfrac{23}{3}\\
&=3\left(x^2-\dfrac{4}{3}x+\dfrac{4}{9}\right)+\dfrac{23}{3}\\
&=\left(3x^2-4x+\dfrac{4}{3}\right)+\dfrac{23}{3}\\
&=3x^2-4x+\dfrac{27}{3}\\
&=3x^2-4x+9
\end{align*}
Hence, the parabola has a vertex at $\left(\dfrac{2}{3},\dfrac{23}{3}\right)$ and vertex form $y=3\left(x-\dfrac{2}{3}\right)^2+\dfrac{23}{3}$.
- Use the vertex formula to solve for the coordinates of the vertex of the parabola $y=5x^2+10x-2$. Then express the equation of the parabola in vertex form.
The parabola has coefficients $a=5$, $b=10$, and $c=-2$. The vertex of the parabola has coordinates
$$h=-\dfrac{10}{2(5)}=-\dfrac{10}{10}=-1$$
and
$$k=-\dfrac{(10)^2-4(5)(-2)}{4(5)} =-\dfrac{100+40}{20}=-\dfrac{140}{20}=-7.$$
The vertex of the parabola is the point $(-1,-7)$. The vertex form of the parabola is given by
\begin{align*}
y&=5(x-(-1))^2-7\\
y&=5 (x+1)^2-7.
\end{align*}
How Is the Vertex Formula Derived?
The vertex formula is derived from the standard form of the equation of the parabola that is transformed into the vertex form. We start from the equation of the parabola
$$y=ax^2+bx+c.$$
We subtract both sides by $c$,
$$y-c=ax^2+bx.$$
Then we factor out the coefficient of the first term,
$$y-c=a\left(x^2+\dfrac{b}{a}x\right).$$
Take the expression $x^2+\dfrac{b}{a}x$ and make it a perfect square trinomial. Recall the form and factors of a perfect square trinomial,
$$x^2+2mx+m^2=(x+m)^2.$$
Thus, the coefficient of the middle term is in the form of $2m$ and the last term is $m^2$. Applying this to the $x^2+\dfrac{b}{a}x$, we have
\begin{align*}
2m&=\dfrac{b}{a}\\
\Rightarrow m&=\dfrac{b}{2a}\\
\Rightarrow m^2&=\left(\dfrac{b}{2a}\right)^2=\dfrac{b^2}{4a^2}.
\end{align*}
So, we add $\dfrac{b^2}{4a^2}$ to the expression $x^2+\dfrac{b}{a}x$ to make it a perfect square. Then, we have
$$x^2+\dfrac{b}{a} x+\dfrac{b^2}{4a^2}=\left(x+\dfrac{b}{2a}\right)^2.$$
Note that
$$a\left(x^2+\dfrac{b}{a}x+\dfrac{b^2}{4a^2}\right)=ax^2+bx+\dfrac{b^2}{4a}.$$
This means that to preserve the equality, when we add $\dfrac{b^2}{4a^2}$ inside the expression $x^2+\dfrac{b}{a}x$, we have to also add $-\dfrac{b^2}{4a}$.
\begin{align*}
y-c&=a\left(x^2+\dfrac{b}{a}x+\dfrac{b^2}{4a^2}\right)-\dfrac{b^2}{4a}\\
y-c&=a\left(x+\dfrac{b}{2a}\right)^2-\dfrac{b^2}{4a}.
\end{align*}
We now write it as an equation for $y$,
\begin{align*}
y&=a\left(x+\dfrac{b}{2a}\right)^2-\dfrac{b^2}{4a}+c\\
y&=a\left(x-\left(-\dfrac{b}{2a}\right)\right)^2-\dfrac{b^2-4ac}{4a}\\
\Rightarrow y&=a\left(x-\left(-\dfrac{b}{2a}\right)\right)^2+\left(-\dfrac{b^2-4ac}{4a}\right).
\end{align*}
Comparing it to the vertex form $y=a(x^2-h)^2+k$, we have the formula for $h$ and $k$.
$$h=-\dfrac{b}{2a}$$
and
$$k=-\dfrac{b^2-4ac}{4a}.$$
Notice also that the numerator of $k$ is the discriminant of the quadratic formula.
Example 3
Use the parabola $y=5x^2+10x-2$ in Example 2 and transform it into the vertex form to determine the vertex $(h,k)$ without using the vertex formula.
We write the standard equation and add $2$ on both sides:
\begin{align*}
y&=5x^2+10x-2\\
y+2&=5x^2+10x\\
y+2&=5(x^2+2x).
\end{align*}
We take the expression $x^2+2x$ and complete it to make it a perfect square trinomial.
Let $p^2$ be the last term so that $x^2+2x+p^2$ is a perfect square. Thus, the coefficient of the middle term is $2p$. That is,
\begin{align*}
2p&=2\\
\Rightarrow p&=1.
\end{align*}
So, we have
$$x^2+2x+1=(x+1)^2.$$
Since we will add $1$ inside the expression, then we need to add $-5$.
\begin{align*}
y+2&=5(x^2+10x+1)-5\\
y+2&=5(x+1)^2-5\\
y&=5(x+1)^2-5-2\\
y&=5 (x+1)^2-7\\
\Rightarrow y&=5(x-(-1))^2+(-7)
\end{align*}
The equation of the parabola is now transformed in the vertex form, so we can now identify the vertex of the parabola which is the point $(-1,-7)$.
We verify that we get the same vertex and vertex form of the equation for this parabola without using the vertex formula.
How To Find the Vertex of a Function?
There are two ways to find the vertex of a function – (1) using the vertex formula, and (2) transforming the standard equation into the vertex form. We get the same coordinates of the vertex $(h,k)$ of the parabola using any of these methods.
The quadratic function $f(x)=ax^2+bx+c$ has a graph of a parabola with vertex at $(h,k)$ where the values of the coordinates are derived by:
- Using the vertex formula
\begin{align*}
h&= -\dfrac{b}{2a}\\
k&=-\dfrac{b^2-4ac}{4a}.
\end{align*} - Converting the equation into the vertex form
$$f(x)=a(x-h)^2+k.$$
Study the following example to find the vertex of a function using each method.
Example 4
- Find the vertex of the parabola described by the quadratic function $f(x)=-6x^2+24-27$.
Some Observations
- You can use any method that you think is easier to use. Here are some tips.
- Use the vertex formula if the coefficients of the quadratic function are relatively small, meaning $b^2$ is not too large. Sometimes, parabola with smaller coefficients gives fraction values to the coordinates of the vertex (like in Example 1). Usually, these types of quadratic functions are harder to transform into vertex forms because they involve fractions.
- Converting into the vertex form is easier for quadratic equations with larger coefficients. You just need to familiarize yourself with completing the expression to turn them into a perfect square trinomial.
- If the parabola has no middle term, that is, it is in the form $y=ax^2+c$, then the vertex is located at a point on the y-axis.
If a parabola has no middle term, then $b=0$. Thus,
$$h=-\dfrac{b}{2a}=-\dfrac{0}{2a}=0.$$
Then, the vertex is at $(0,k)$ which is the y-intercept of the parabola.
Conclusion
The vertex formula is a useful tool in determining the vertex of a parabola. While it gives us the exact values of the coordinates of the vertex, it is also deemed a handful in working with quadratic functions with large coefficients. We also discussed transforming the standard form of the equation of a parabola into its vertex form as an alternative for using the vertex formula in identifying the vertex.
- The vertex formula gives the values of the coordinates of the vertex $(h,k)$ where $h=-\dfrac{b}{2a}$ and $k=-\dfrac{b^2-4ac}{4a}$.
- The vertex form of the parabola is the equation $y=a(x-h)^2+k$, where $(h,k)$ is the vertex.
- The vertex formula is derived by transforming the standard equation into the vertex form.
- There two methods for finding the vertex of the function: (1) using the vertex formula and (2) expressing the equation of the parabola into its vertex form.
- The vertex of the parabola is located in the y-axis if the parabola has no middle term.
Locating the vertex of a parabola is important in describing the parabola and giving some indications of the behavior of the parabola, and once you know how to determine the vertex, you can solve for the other significant points in the graph of the parabola.
Images/mathematical drawings are created with GeoGebra.