
This article will delve into the LIATE rule, offering a comprehensive understanding of its significance, application, and how it contributes to easing the complex integration process.
Defining LIATE
LIATE is an acronym that stands for Logarithmic, Inverse trigonometric, Algebraic, Trigonometric, and Exponential functions. It is a rule of thumb to help you choose the “u” function when using the integration by parts formula.
The integration by parts formula is an integral analog to the product rule for differentiation. It is given as follows:
∫u dv = u v – ∫v du
When applying the integration by parts formula, we typically have to choose the functions ‘u’ and ‘dv’ from a given integrand that is a product of two functions. The choice of ‘u’ can greatly simplify the integration process. That’s where the LIATE rule comes in.
According to the LIATE rule, one should choose ‘u’ from the given integrand in the following priority order:
- L: Logarithmic functions, such as ln(x)
- I: Inverse trigonometric functions, such as arcsin(x), arccos(x), arctan(x)
- A: Algebraic functions, like polynomials or root functions
- T: Trigonometric functions, such as sin(x), cos(x), tan(x), cot(x)
- E: Exponential functions, such as eˣ, aˣ
Like all rules of thumb, LIATE is not a hard-and-fast rule. There are exceptions where the choice of ‘u’ may deviate from this order to simplify the integral. But in most cases, it proves to be a helpful guide.
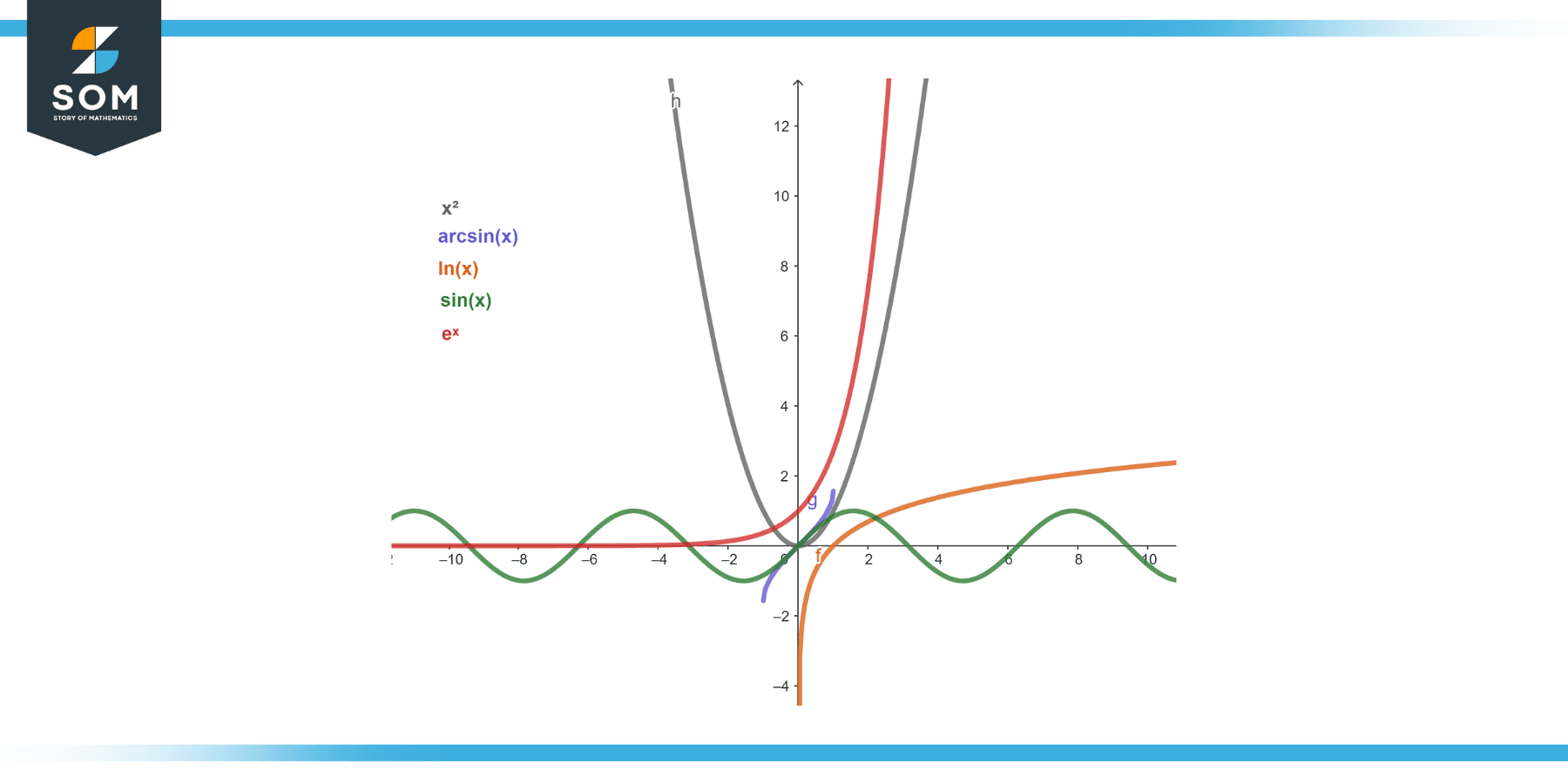
Figure-1.
Properties of LIATE Rule
The LIATE rule, as a mnemonic device, helps mathematicians remember the priority order for selecting the ‘u‘ function when using the method of integration by parts. LIATE stands for Logarithmic, Inverse trigonometric, Algebraic, Trigonometric, and Exponential functions. The properties or aspects related to each part of LIATE are as follows:
L (Logarithmic Functions)
These functions are based on logarithms. The natural logarithm function ln(x) is the most commonly used, but others, such as log base 10 or any other base, can also be involved. In the context of the LIATE rule, if a logarithmic function is a factor of the integrand in an integration problem, it’s typically a good candidate to select as ‘u‘ in the integration by parts formula.
I (Inverse Trigonometric Functions)
Inverse trigonometric functions, such as arcsin(x), arccos(x), arctan(x), arccsc(x), arccot(x), and arcsec(x), return the angle for a given ratio in a right triangle. In the LIATE rule, if there is an inverse trigonometric function in the integrand, it takes the second priority after logarithmic functions to be chosen as ‘u‘ in the integration by parts formula.
A (Algebraic Functions)
Algebraic functions are any function that polynomial expressions can define. They include polynomials, root functions, and rational functions. In the context of the LIATE rule, an algebraic function should be chosen as ‘u‘ only if there are no logarithmic or inverse trigonometric functions in the integrand.
T (Trigonometric Functions)
Trigonometric functions are based on the ratios of the sides of a right triangle to its angles. They include sin(x), cos(x), tan(x), cot(x), sec(x), and csc(x). In the LIATE rule, a trigonometric function should be chosen as ‘u‘ only if there are no logarithmic, inverse trigonometric, or algebraic functions in the integrand.
E (Exponential Functions)
Exponential functions have a variable in the exponent, like eˣ or aˣ, where ‘a’ is a constant. According to the LIATE rule, these functions are usually the last to be selected as ‘u‘ in the integration by parts formula.
Ralevent Formulas
The LIATE rule is a heuristic used to determine the order of functions in the integration by parts formula. Here’s a reminder of the LIATE rule:
- L: Logarithmic functions, such as ln(x)
- I: Inverse trigonometric functions, such as arctan(x) or arcsin(x)
- A: Algebraic functions, like polynomials x² or radicals √x
- T: Trigonometric functions, like sin(x), cos(x), etc.
- E: Exponential functions, such as eˣ, aˣ
The basic formula for integration by parts is:
∫u dv = u v – ∫v du
When we have a product of functions to integrate, we choose which function to be “u” and which to be “dv” based on the LIATE rule. The function that comes first in the LIATE rule is chosen as “u” while the remaining function is “dv.” Then we find “du” by differentiating “u” and “v” by integrating “dv.”
In the context of the LIATE rule, there isn’t a specific formula. However, it’s a method to apply the formula for integration by parts. The LIATE rule helps determine the choice of “u” and “dv” when applying integration by parts.
For example, if we want to integrate x * eˣ dx, following the LIATE rule, we’d choose u = x (Algebraic) and dv = eˣ dx (Exponential). Then du = dx, v = eˣ, and the integration by parts formula give:
∫x eˣ dx = x eˣ – ∫eˣ dx
∫x eˣ dx = x eˣ – eˣ + C
The rule doesn’t always work perfectly, and sometimes you might need to apply integration by parts more than once or use a different method. But it’s a helpful guideline when first setting up the integral.
Exercise
Example 1
Problem: ∫x ln(x) dx
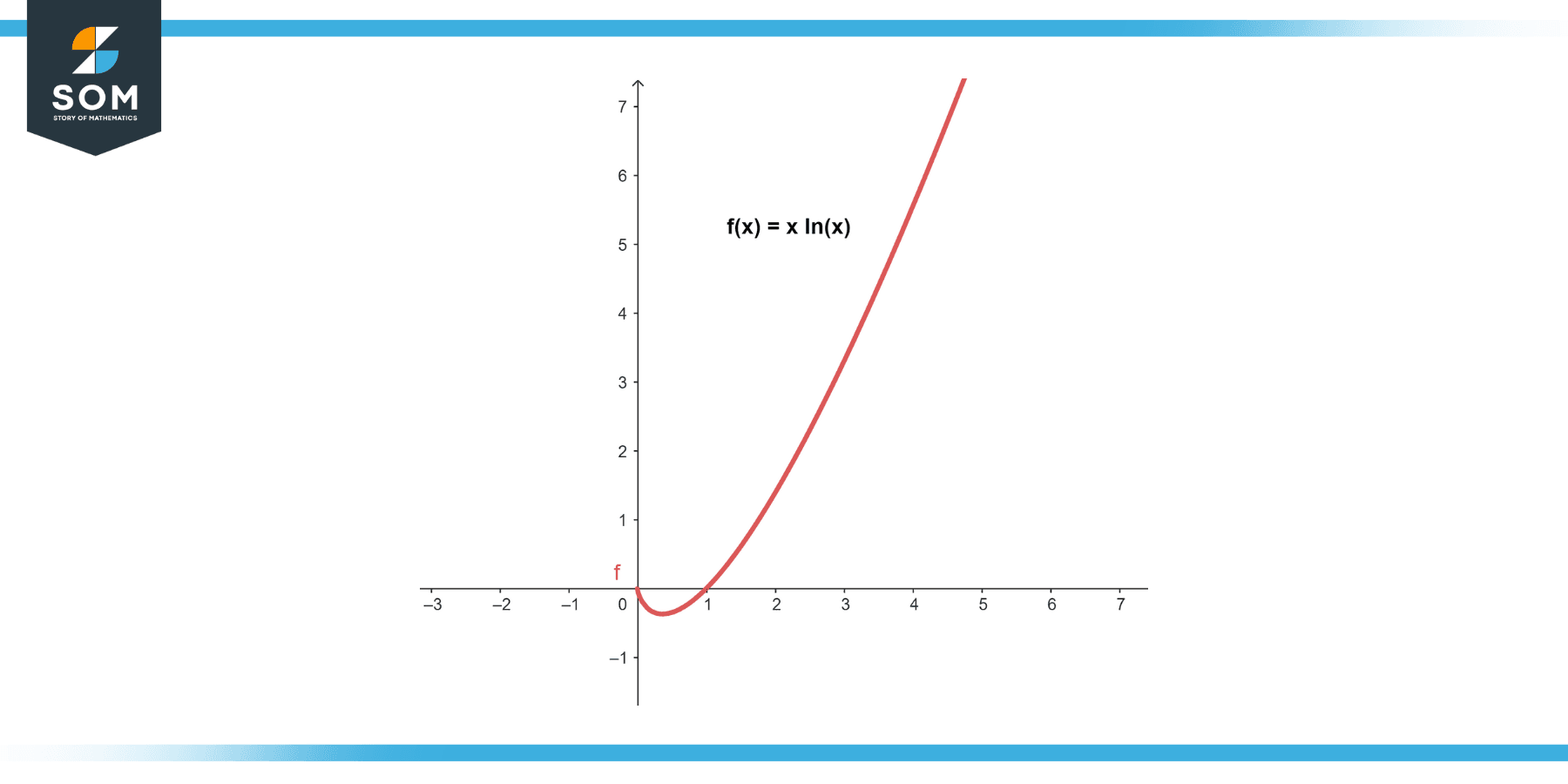
Figure-2.
Solution
Here, let u = ln(x) (L in LIATE) and dv = x dx (A in LIATE). Then, du = dx/x and v = 0.5 * x². Using the formula for integration by parts, ∫u dv = u v – ∫v du, we get:
∫x ln(x) dx = 0.5x² ln(x) – ∫0.5x dx
∫x ln(x) dx = 0.5x² ln(x) – 0.25x² + C
Example 2
Problem: ∫x eˣ dx
Solution
Here, let u = x (A in LIATE) and dv = eˣ dx (E in LIATE). Then, du = dx and v = eˣ. Applying the integration by parts formula, we get:
∫x eˣ dx = x eˣ – ∫eˣ dx
∫x eˣ dx = x eˣ – eˣ + C
Example 3
Problem: ∫x sin(x) dx
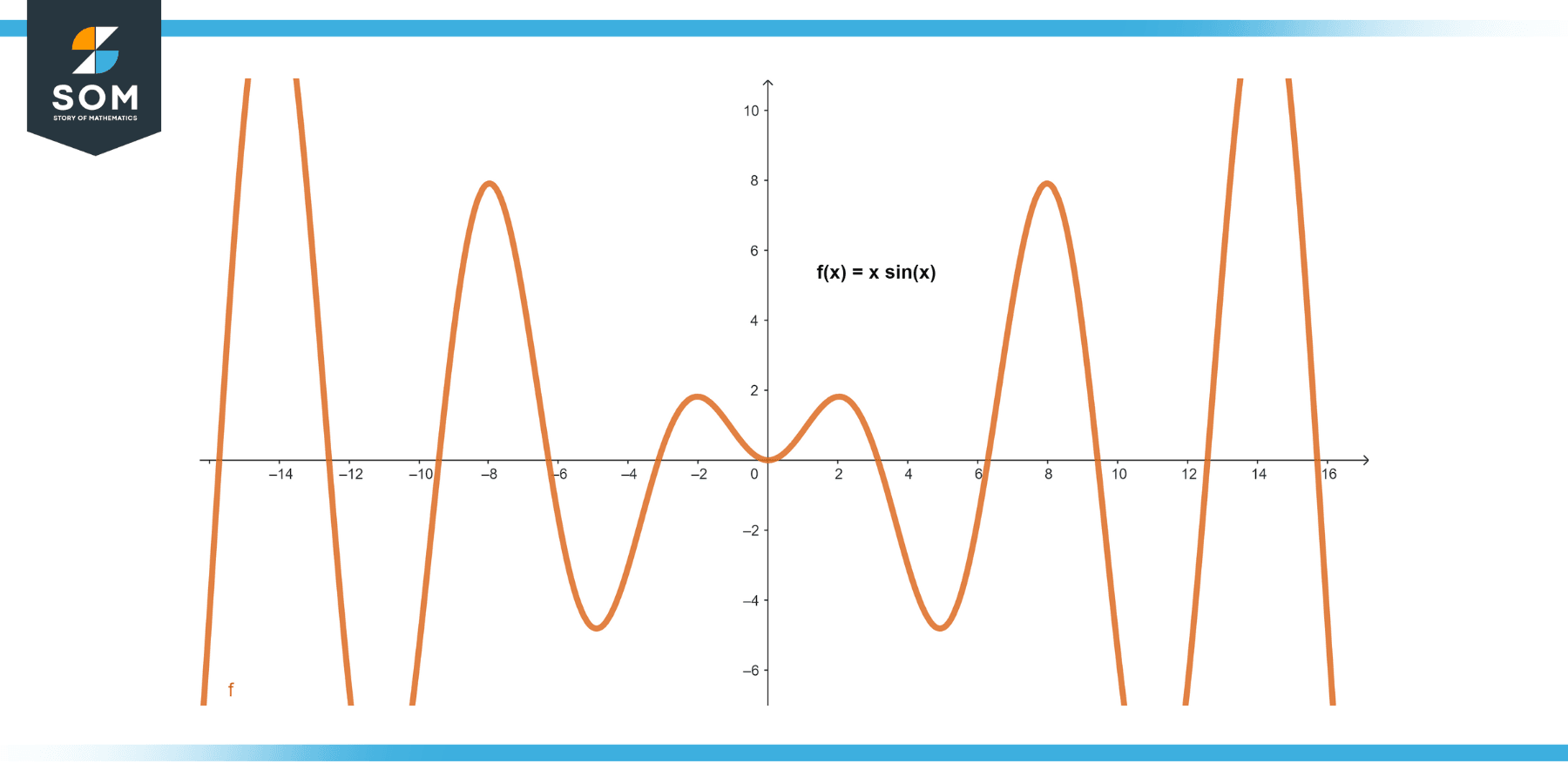
Figure-3.
Solution
Here, let u = x (A in LIATE) and dv = sin(x) dx (T in LIATE). Then, du = dx and v = -cos(x). Applying the integration by parts formula, we get:
∫x sin(x) dx = -x cos(x) – ∫-cos(x) dx
∫x sin(x) dx = -x cos(x) + sin(x) + C
Example 4
Problem: ∫x² ln(x) dx
Solution
Here, we will use integration by parts twice. First, let u = ln(x) (L in LIATE) and dv = x² dx (A in LIATE). Then, du = dx/x and v = (1/3) * x³. Applying the integration by parts formula, we get:
∫x² ln(x) dx = (1/3) * x³ ln(x) – ∫(1/3) * x² dx
∫x² ln(x) dx= (1/3) * x³ ln(x) – (1/9) * x³ + C
Example 5
Problem: ∫x² eˣ dx
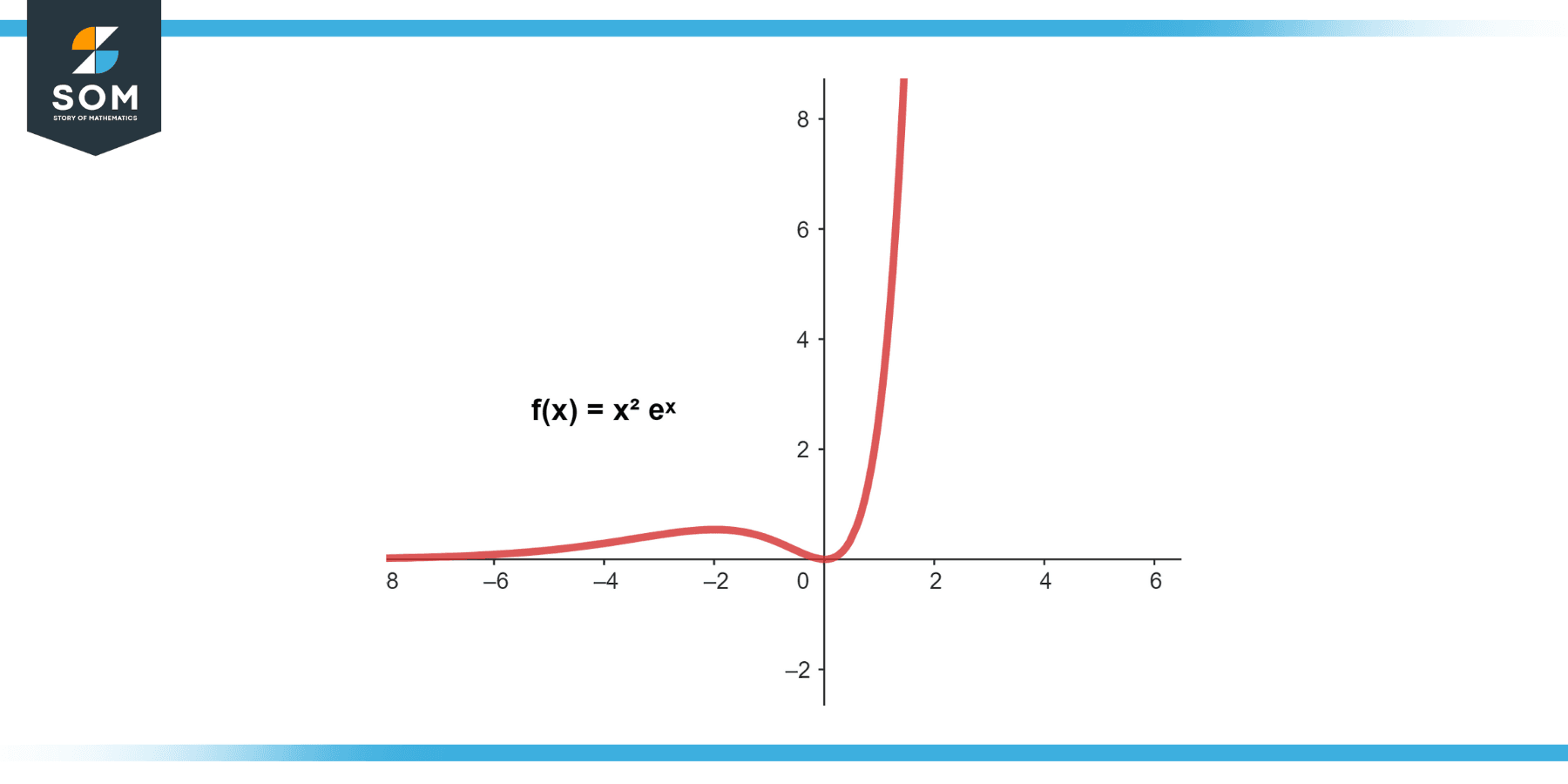
Figure-4.
Solution
Here, we will also use integration by parts twice. First, let u = x² (A in LIATE) and dv = eˣ dx (E in LIATE). Then, du = 2 * x dx and v = eˣ. Applying the integration by parts formula, we get:
∫x² * eˣ dx = x² eˣ – ∫2 * x eˣ dx
Now, we will use integration by parts for the second integral: Let u = 2x (A in LIATE) and dv = eˣ dx (E in LIATE). Then, du = 2 dx and v = eˣ. Again applying the formula, we get:
∫2 * x eˣ dx = 2x eˣ – ∫2 e^x dx
∫2 * x eˣ dx = 2x eˣ – 2 eˣ + C
Substituting this back into the first integral, we get:
∫x² eˣ dx = x² eˣ – (2x eˣ – 2 eˣ) + C
∫x² eˣ dx = (x² – 2x + 2) * eˣ + C
Example 6
Problem: ∫ln(x)/x dx
Solution
Here, let u = ln(x) (L in LIATE) and dv = dx/x (A in LIATE). Then, du = dx/x and v = 1. Applying the integration by parts formula, we get:
∫ln(x)/x dx = ln(x) – ∫dx
∫ln(x)/x dx = ln(x) – x + C
Example 7
Problem: ∫x arctan(x) dx
Solution
Here, let u = arctan(x) (I in LIATE) and dv = x dx (A in LIATE). Then, du = dx/(1 + x²) and v = 0.5 * x². Applying the integration by parts formula, we get:
∫x arctan(x) dx = 0.5 * x² * arctan(x) – ∫0.5 * x² dx/(1 + x²)
This integral would further require partial fraction decomposition to solve completely.
Example 8
Problem: ∫x ln(x) eˣ dx
Solution
This is a complex problem that would require using integration by parts multiple times and applying the LIATE rule appropriately. Each integration by parts would reduce the degree of the algebraic part until it becomes a simple function. It’s beyond the scope of this brief explanation, but it’s a good exercise to work through!
Applications
Engineering
Many engineering problems involve the evaluation of integrals that arise in the context of physical phenomena. The LIATE rule can be particularly useful for performing these integrations. For instance, in Electrical Engineering, the circuits’ voltage and current calculations often require the integration of functions that can be solved using the LIATE rule.
Mathematics
By following the LIATE rule, mathematicians can often select the most appropriate functions for differentiation and integration, leading to more efficient and successful integration by parts computations.
However, it’s important to note that the LIATE rule is a guideline, not a strict one. There may be cases where a different order of functions works better depending on the problem.
Physics
The LIATE rule is often used in Physics to solve various problems, especially in Quantum Mechanics, where wave functions often need to be integrated to find probabilities. It is also used in Classical Mechanics for solving problems related to motion, energy, and momentum.
Economics and Finance
In these fields, the LIATE rule can solve integrals in models involving continuous time, such as certain economic growth models or option pricing models in finance.
Biology and Medicine
The LIATE rule can help integrate functions that model biological systems or processes, such as drug concentration in the bloodstream over time or the population dynamics of species.
Computer Science
In algorithm analysis, integrals often appear when dealing with continuous approximations of discrete problems. The LIATE rule can be used to solve such integrals, which might involve, for example, the running time of an algorithm as a function of the input size.
By applying the LIATE rule, researchers can select appropriate functions for integration and analyze the efficiency and behavior of algorithms in a continuous context. This aids in understanding the scalability and performance of algorithms as the input size increases.
Statistics and Data Science
In statistics, many problems involve the computation of expectations, variances, and other moments, which require integration. The LIATE rule is often used to solve these kinds of problems.
All images were created with GeoGebra.
