JUMP TO TOPIC
A line of reflection is a line that lies between two identical mirror images, so the distance of any point of one figure from the line will equal the distance of the same point of the mirror image (flipped figure).
The definition tells us that if we are given two images, such as mirror images of each other, the line of reflection can be determined by calculating the midpoint from any two points of the figures.
We use the concept of line of reflection in navigation, engineering landscaping, geometry, and art classes. It has many applications in real life; the good news is that it is quite easy to understand.
In this article, we will study the concept of reflection, line of reflection, and related numerical examples.
What Is Line of Reflection?
The line across which the figure is flipped is known as the mirror line or the line of reflection. How do you find the line of reflection between two points? We can draw the line of reflection by finding the mid-point of the given two points; the line should pass through the midpoint.
Mirror Image
Let’s first discuss what is meant by a mirror image. Say you are standing in front of a mirror; the image of yourself in the mirror is a mirror image. For example, if you raise your right arm, then you will observe that your image will also be raising his right arm, but that the right arm of the image will be in front of your left arm. The same is the case with geometrical figures.
For example, if we have a polygon and we reflect it along an axis, then you will notice that the shape and size of both figures remain the same. Only the direction of the figures will be opposite. The most important feature during this reflection process is that the points of the original figure will be equidistant to the points of the reflected figure or the mirror figure/image.
As the points of the original polygon are equidistant from the flipped polygon, if we calculate the mid-point between two points and draw a straight line in such a manner that it is parallel to both figures, then it will be our line of reflection.
Reflection
A reflection is a type of transformation in which we flip a figure around an axis in such a way that we create its mirror image. So if we have a graphical figure or any geometrical figure and we reflect the given figure, then we will create a mirror image of the said figure.
The process of reflection and the line of reflection are co-related. We can draw the line of reflection according to the type of reflection to be performed on a given figure. Simple reflection is different from glide reflection as it only deals with reflection and doesn’t deal with the transformation of the figure.
Types of Reflection
We can perform the reflection of a given figure over any axis. The reflection of any given polygon can be of three types:
- Reflection over x-axis
- Reflection over y-axis
- Reflection over the x and y axis
Reflection Over X-axis
When we reflect a figure or polygon over the x-axis, then the x-coordinates of all the vertices of the polygon will remain the same while the sign of the y-coordinate will change. For example, consider a triangle with the vertices $A = (5,6)$ , $B = (3,2)$ and $C = (8,5)$ and if we reflect it over the x-axis then the vertices for the mirror image of the triangle will be $A^{‘} = (5,-6)$ , $B^{‘} = (3,2)$ and $C^{‘} = (8,5)$.
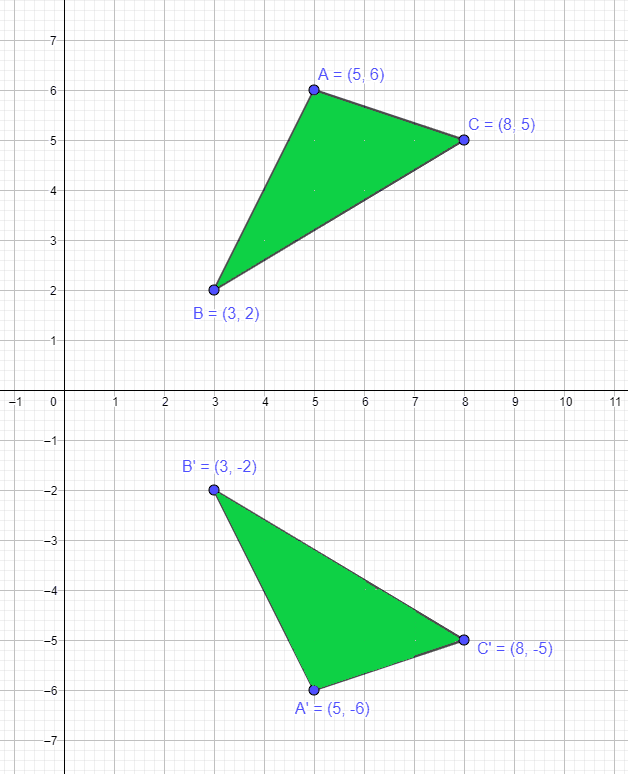
Line of Reflection for Reflection Over the X-axis
The line of reflection will be the x-axis when a figure is reflected across the x-axis. Taking the previous example of the triangle with the vertices $A = (5,6)$ , $B = (3,2)$ and $C = (8,5)$ and after the reflection the vertices became $A^{‘} = (5,-6)$ , $B^{‘} = (3,2)$ and $C^{‘} = (8,5)$. Take note of the picture given below.
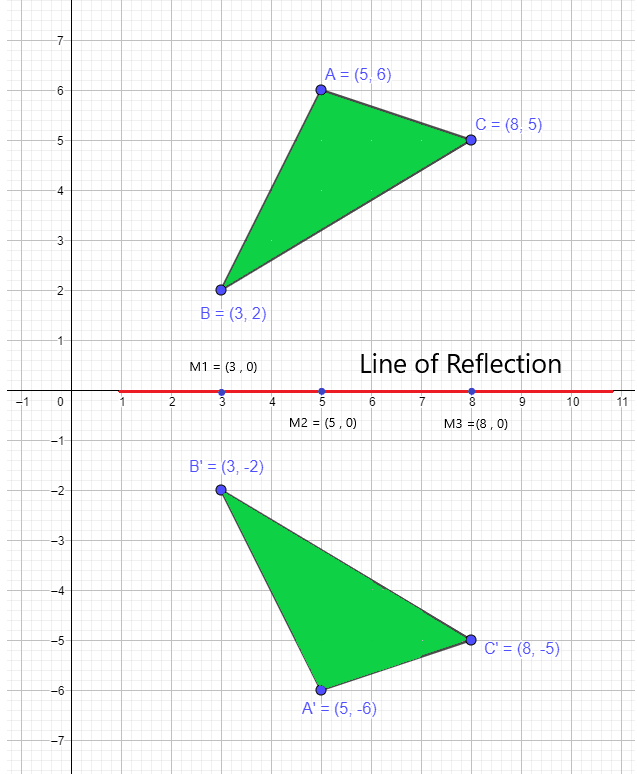
We know that the point of the original polygon is equidistant from the flipped polygon. Calculating the mid-points between all the vertices and then joining those mid-points will give us our line of reflection for this example. We can calculate Mid-point between the points as:
Mid – point $= (\dfrac{x_{1} + x_{2}}{2}),(\dfrac{y_{1} + y_{2}}{2})$
Midpoint of $A$ and $A^{‘} = (\dfrac{5 + 5}{2}),(\dfrac{6 – 6 }{2}) = (5,0 )$
Mid point of $B$ and $B^{‘}$ = $(\dfrac{3 + 3}{2}),(\dfrac{2 – 2 }{2}) = (3,0 )$
Mid point of $C$ and $C^{‘}$ = $(\dfrac{8 + 8}{2}),(\dfrac{5 – 5 }{2}) = (8,0 )$
If we join the points $(5,0)$, $(3,0)$, and $(8,0)$, it will give us our line of reflection. We can extend the line and say that the line of reflection is x-axis when a polygon is reflected over the x-axis.
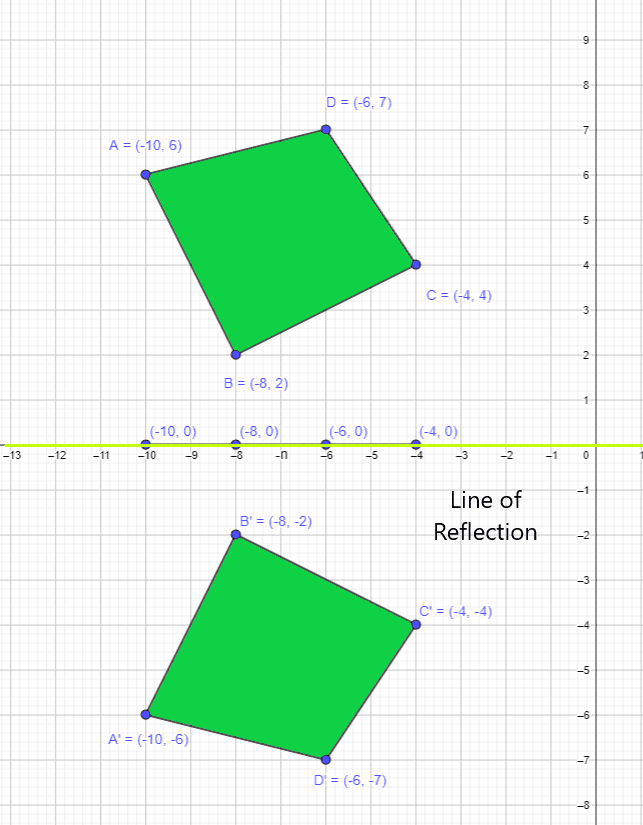
Example 1: A polygon with the vertices $A = (-10,6)$ , $B = (-8,2)$, $C = (-4,4)$ and $D = (-6,7)$ is reflected over the x-axis. You are required to find out the midpoints and draw the line of reflection.
Solution:
We are given a quadrilateral figure and if we reflect it over the x-axis, the corresponding vertices will be $A^{‘} = (-10,-6)$ , $B^{‘} = (-8,-2)$, $C^{‘} = (-4,-4)$ and $D^{‘} = (-6,-7)$.
We can calculate Mid-point between the points as:
Mid – point $= (\dfrac{x_{1} + x_{2}}{2}),(\dfrac{y_{1} + y_{2}}{2})$
Mid-point of $A$ and $A^{‘} = (\dfrac{-10 – 10}{2}), (\dfrac{6 – 6 }{2}) = (-10,0 )$
Mid-point of $B$ and $B^{‘} = (\dfrac{-8 – 8}{2}), (\dfrac{2 – 2 }{2}) = (-8,0 )$
Mid-point of $C$ and $C^{‘} = (\dfrac{-4 – 4}{2}), (\dfrac{4 – 5 }{2}) = (-4,0 )$
Mid-point of $D$ and $D^{‘} = (\dfrac{-6 – 6}{2}), (\dfrac{7 – 7 }{2}) = (-6,0 )$
When we join the points, we see that the line of reflection is the x-axis.
Reflection Over Y-axis
When we reflect a figure or polygon over the y-axis, then the y-coordinates of all the vertices of the polygon will remain the same while the sign of the x-coordinates will change. For example, if a point $(3,7)$ is present in the first quadrant and we reflect it over the y-axis, then the resulting point will be $(3,-7)$.
Line of Reflection for Reflection Over the Y-axis
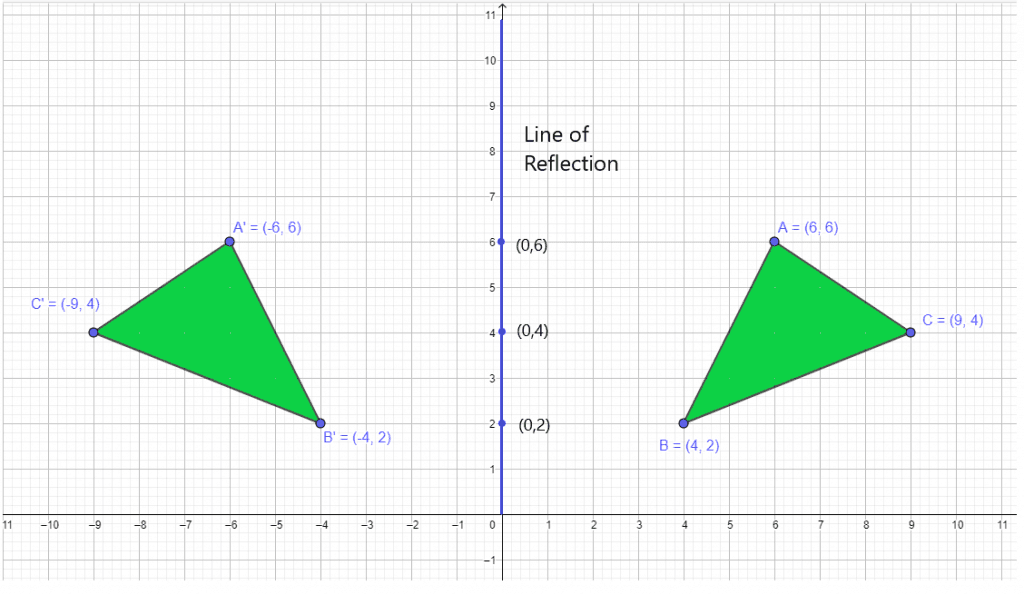
The line of reflection is along the y-axis when a figure is rotated over the y-axis. Consider a triangle with the vertices $A = (6,6)$ , $B = (4,2)$ and $C = (9,4)$ and if we reflect it over the y-axis, then the vertices for the mirror image of the triangle will be $A^{‘} = (-6,6)$ , $B^{‘} = (-6,2)$ and $C^{‘} = (-9,4)$.
We can calculate Mid-point between the points as:
Mid – point $= (\dfrac{x_{1} + x_{2}}{2}), (\dfrac{y_{1} + y_{2}}{2})$
Mid-point of $A$ and $A^{‘} = (\dfrac{6, – 6}{2}), (\dfrac{6 + 6 }{2}) = (0, 6)$
Mid-point of $B$ and $B^{‘} = (\dfrac{4 – 4}{2}), (\dfrac{2 + 2 }{2}) = (0, 2)$
Mid-point of $C$ and $C^{‘} = (\dfrac{9 – 9}{2}), (\dfrac{4 + 4 }{2}) = (0, 4)$
As the x-coordinate value of all the vertices is zero, the line of reflection will be the y-axis. You can join all the midpoints and see that the line will lie on the y-axis, as shown below.
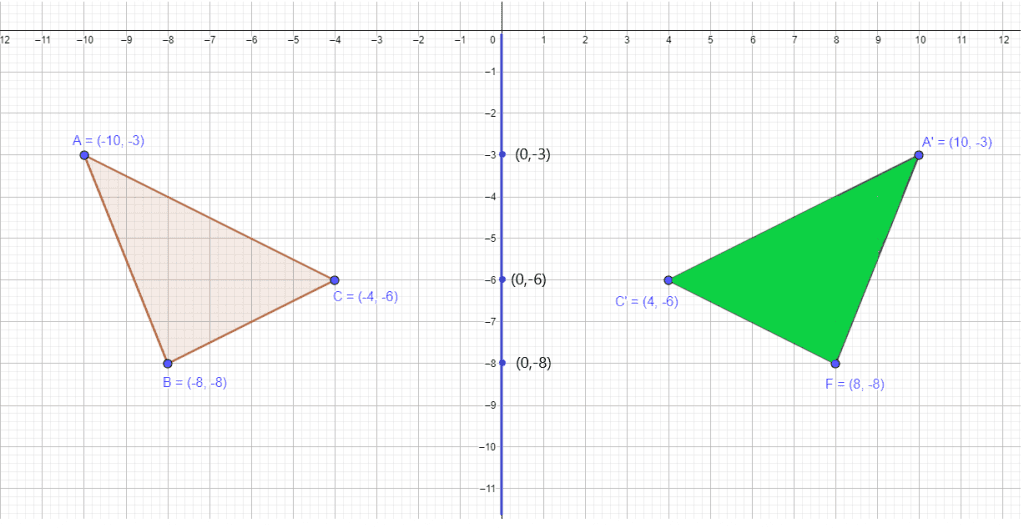
Example 2: A polygon with the vertices $A = (-10,-3)$ , $B = (-8,-8)$ and $C = (-4,-6)$ is reflected over the y-axis. You are required to find out the midpoints and draw the line of reflection.
Solution:
We are given a quadrilateral figure and if we reflect it over the x-axis, the corresponding vertices will be $A^{‘} = (10,-3)$ , $B^{‘} = (8,-8)$ and $C^{‘} = (4,-6)$.
We can calculate mid-point between the points as:
Mid-point of $A$ and $A^{‘} = (\dfrac{-10 + 10}{2}), (\dfrac{-3 – 3 }{2}) = (0,-3 )$
Mid point of $B$ and $B^{‘} = (\dfrac{-8 + 8}{2}), (\dfrac{-8 – 8 }{2}) = (0,-8 )$
Mid point of $C$ and $C^{‘} = (\dfrac{-4 + 4}{2}), (\dfrac{-6 – 6 }{2}) = (0,-6 )$
When we join the points, we see that the line of reflection is along the y-axis.
Reflection Over X and Y-axis
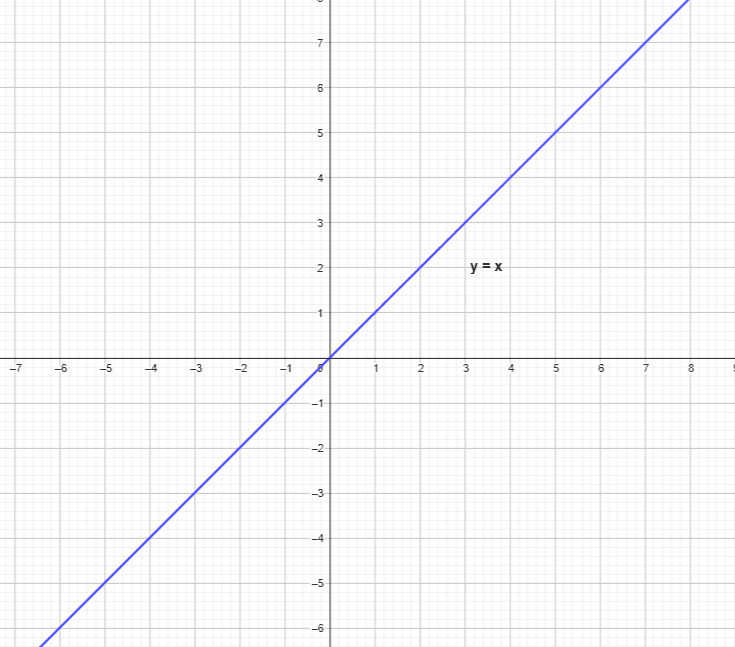
When a point or figure is reflected across the x-axis and the y-axis, we write that the line is reflected over $x = y$. We write it as a reflection of a function of over $x = y$. This type of reflection can further be divided into two scenarios: a) $y = x$ and b) $y = -x $.
When the point or figure is reflected over $y = x$, we swap the coordinates of the x-axis and y-axis. For example, if a point $(6,5)$ is reflected over $y = x$, the corresponding point will be $(5,6)$.
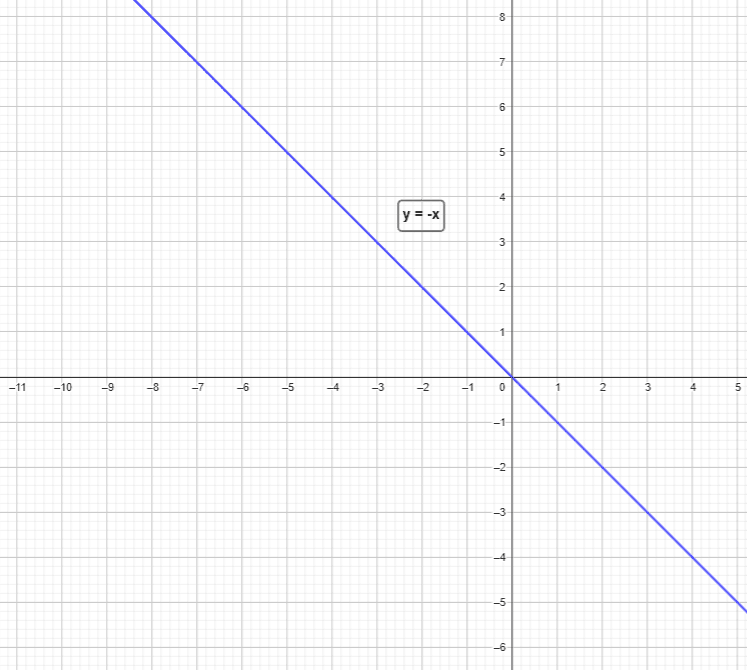
When the point or figure is reflected over $y = -x$, then the sign of the coordinates of the x-axis and y-axis are reversed, and just like in the previous case, the coordinates are swapped as well. For example, if a point $(6,-5)$ is reflected over $y = -x$, then the corresponding point will be $(5,-6)$.
Line of Reflection y=x or y=-x
The equation $y = x$ and $y = -x$ represents a line. So when we say a point or figure is reflected over $y = x$, the point or figure is reflected over the line $y = x$, and the equation $y = x$ is the line of reflection in this case. It is shown as:
Similarly, when a point or figure is reflected over $y = -x$, this means the point or figure is reflected over the line $y = -x$, and the equation $y = -x$ is the line of reflection. In this case, it is shown as:
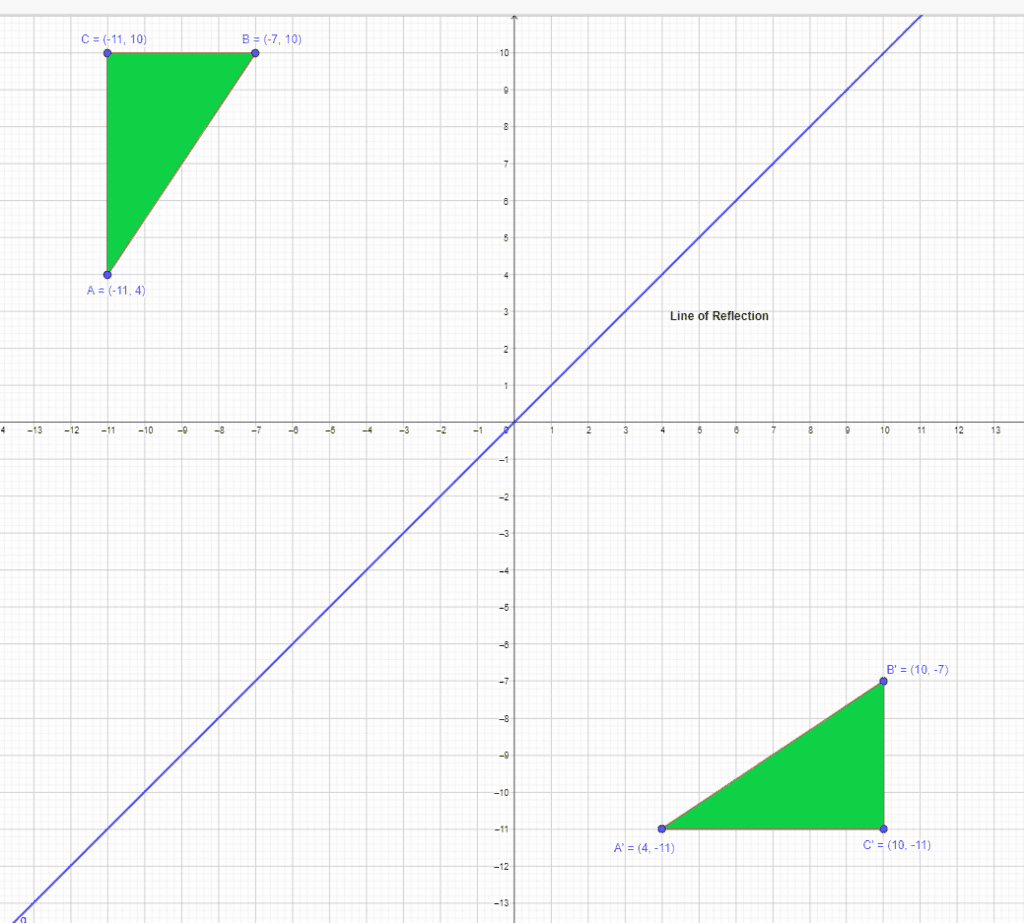
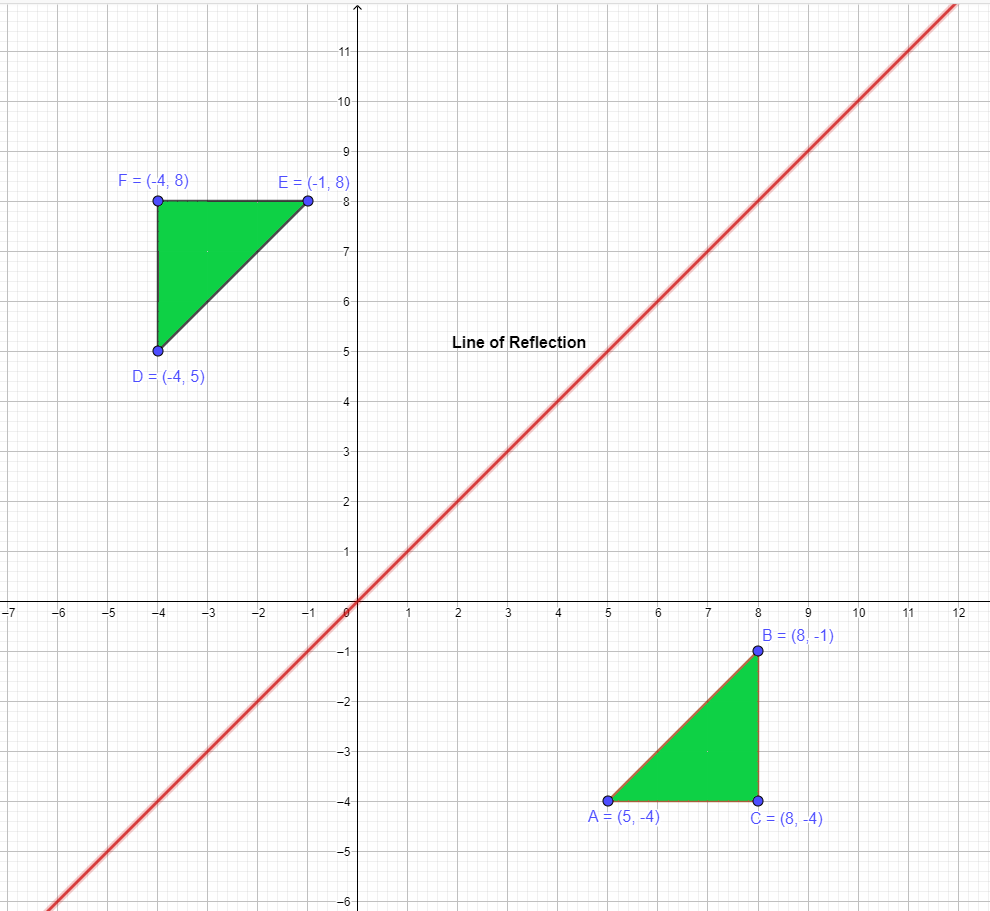
Example 3: A polygon has three vertices $A = (5,-4)$ , $B = (8,-1)$ and $C = (8,-4)$, which are reflected over $y = x$. You are required to show the reflection of the polygon across the line of reflection.
Solution:
When a figure is reflected over $y = x$, the x and y coordinates will be swapped for the mirror image. Hence, the coordinates for mirror image will be $A = (-4,5)$ , $B = (-1,8)$ and $C = (-4,8)$. We show the reflected figure and the line of reflection in the picture below.
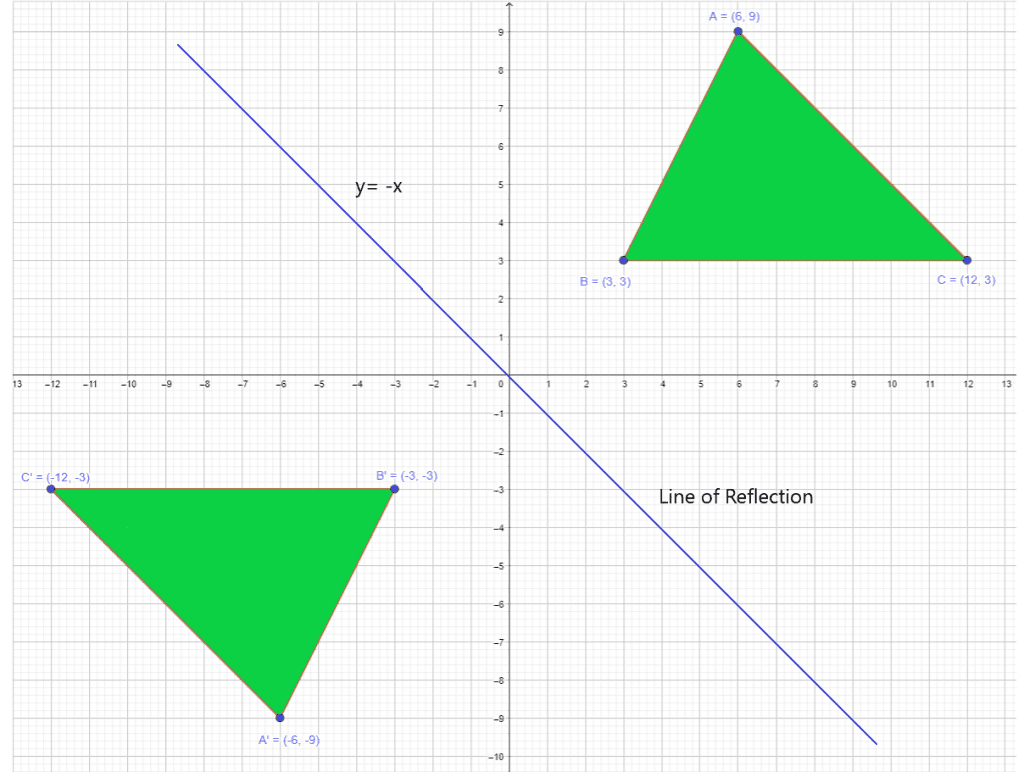
Example 4: A polygon with the vertices $A = (6,-9)$ , $B = (3,3)$ and $C = (12,3)$ is reflected over $y = -x$. You are required to show the reflection of the polygon across the line of reflection.
Solution:
When a figure is reflected over $y = -x$, the sign of both x and y coordinates will be reversed, and the coordinates will be swapped. Hence, the coordinates for mirror image will be $A^{‘} = (-6,-9)$ , $B^{‘} = (-3,-3)$ and $C^{‘} = (-12,-3)$. The reflected figure and the line of reflection are shown in the picture below.
Reflection Over Random Line
When a figure is reflected over a random line, it is reflected in such a way that the whole figure is not flipped over any axis, and some part of the figure remains on the same axis. According to the line of reflection characteristics, we know the line of reflection will be parallel to both images, and the vertices or points of the figures will be at an equal distance from the line of reflection.
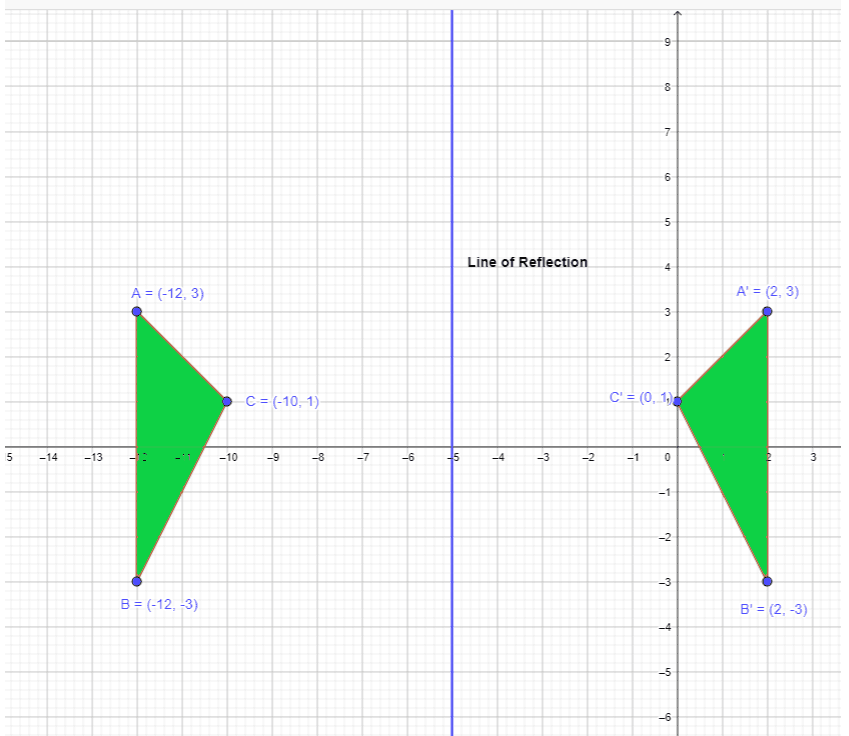
For example, a triangle has vertices $A = (-12,3)$ , $B = (-12,-3)$ and $C = (-10,1)$ and the flipped triangle has vertices $A{‘} = (2,3)$, $B^{‘} = (2,-3)$ and $C^{‘} = (0,1)$. The mid-points can be calculated as:
Mid point of $A$ and $A^{‘} = (\dfrac{-12 + 2}{2}) ,(\dfrac{3 + 3 }{2}) = (5, 3)$
Mid point of $B$ and $B^{‘} = (\dfrac{-12 + 2}{2}) ,(\dfrac{-3 – 3 }{2}) = (5, -3 )$
Mid point of $C$ and $C^{‘} = (\dfrac{-10 + 0}{2}) ,(\dfrac{1 + 1 }{2}) = (-5, 1)$
The points in the original figure and the flipped or mirror figure are at equal distances from the line of reflection.
Practice Problems
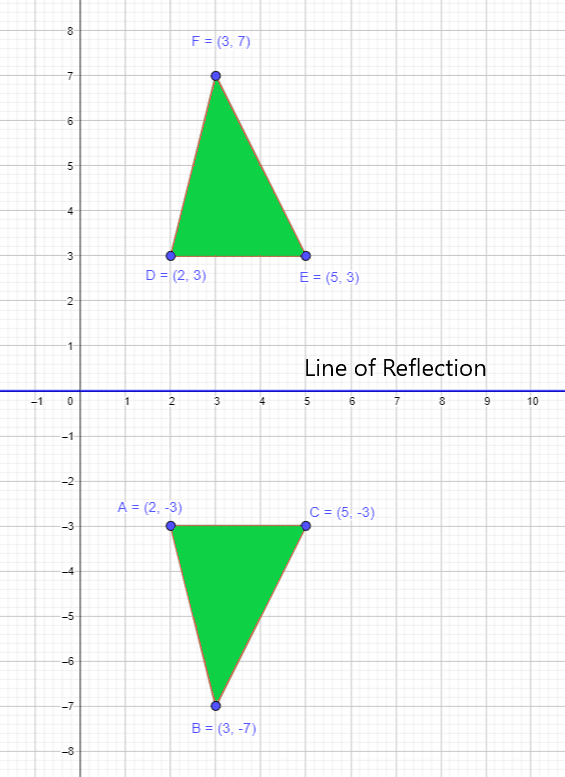
1). A polygon on the coordinate plane has the following vertices: $A = (2,-3)$ , $B = (5,-3)$ and $C = (3,-7)$ reflected over the x-axis. Draw the line of reflection.
2). A polygon has three vertices $A = (5,-4)$ , $B = (8,-1)$ and $C = (8,-4)$ reflected over $y = x$. You are required to show the reflection of the polygon across the line of reflection.
Answer Key
1).
The line of reflection will be on the x-axis, and it is shown in the picture below.
2).
The line of reflection will be y = x, as shown in the picture below.
