JUMP TO TOPIC
 The intercept form of a quadratic equation is used to determine the x-intercepts of the quadratic equation or function.
The intercept form of a quadratic equation is used to determine the x-intercepts of the quadratic equation or function.
The standard form of a quadratic equation is:
$y = ax^{2}+ bx + c$
We can write the intercept form of a quadratic equation as:
$y = a (x-p) (x-q)$
In this article, we will study the concept of intercepts, what is meant by the intercept form of a quadratic equation, and how it helps us when graphing quadratics functions.
What Is the Intercept Form of a Quadratic Equation?
The intercept form of a quadratic equation converts the standard form to the intercept form quadratic, which is then used to determine the x-intercepts of the quadratic equation or function. The intercept form of a quadratic equation is written as:
$y = a (x-p) (x-q)$
Here, “p” and “q” are the x-intercepts of the quadratic equation, and “a” is called the vertical stretching value or factor, and it is used to determine the direction of the parabola. This formula is factored form of the original quadratic formula, and it is also known as x intercept form quadratic.
Intercepts of a Quadratic Function
A quadratic equation or function is a non-linear mathematical expression with a degree of “$2$”. This means that the independent variable will have the power or degree of $2$ in a quadratic equation. When we plot such functions, they form a bell or U shape called a parabola. The place where the parabola crosses an axis is called an intercept. The point where the parabola crosses the x-axis is called the x-intercept, and the point where the parabola crosses the y-axis is called the y-intercept.
The intercept of a quadratic function is the point where the function’s graph intersects or crosses an axis. There are two types of intercept of a quadratic function.
Y-intercept
The point where the graph crosses or intersects the y-axis is called the y-intercept of the quadratic equation or function. We can also determine the y-intercept by putting $x = 0$ in the given quadratic equation.
For example, if we are given a quadratic equation $f(x) = y = 3x^{2}+5x + 6$, then the y-intercept will be $y = 3(0)^{2}+5(0) + 6 = 6$. So, the graph will intersect the y-axis at $y = 6$ at $x = 0$; hence we will write the y-intercept as $(0,6)$.
X-intercept
The point where the graph crosses or intersects the x-axis is called the x-intercept of the quadratic equation or function. The graph of a quadratic function can intersect the x-axis at one or two points. So a quadratic function’s maximum number of x-intercepts will be $2$.
Significance of the Parameters “p” and “q”
Both p and q are called the x-intercepts of the quadratic equation, and we can also call them the roots or solution of the quadratic equation. For example, if we are given a quadratic equation $y = x^{2} -1$, then we can write it as $x^{2}-1 = (x+1) (x-1)$. In this case, the x-intercepts of the equation are “$1$” and “$-1$”, and both these values are also the roots of the quadratic functions.
We know that the graph of a quadratic function is a parabola, and both p and q are used to determine the axis of symmetry for the parabola. The axis of symmetry is the vertical line that intersects the parabola at the vertex point and divides it into two halves. The axis of symmetry can be found by using the formula:
$x = \dfrac{p+q}{2}$
We are taking the average of both intercepts, showing that the axis of symmetry passes through the center of the parabola at the vertex point and divides it into two halves. If the intercepts’ values are the same, then we will write $x = p = q$.
Significance of the parameter “a”
The parameter “a” is also known as the vertical stretching parameter and is used to determine the direction of the parabola. The value of “a” can never be zero because if it is zero, then the quadratic equation simply becomes $x=0$.
If the value of “a” is positive, then this direction or face of the parabola is upwards, and if the value of “a” is negative, then the face of the parabola is in a downward direction.
The magnitude of the parameter “$a$” will define the volume of the parabola. When we talk about the magnitude, we are talking about the absolute value of “$a$”. When the absolute value of “$a$” is above “$1$”, then the parabola face gets narrower as it is vertically stretched, and when the absolute value of “a” is less than “$1$”, then the face of the parabola gets wider.
Let us now study various intercept form quadratic equation examples and learn how to use the intercept form of the quadratic equation to find the roots of the quadratic equation, plus how we can use the intercept form to draw the graph of the quadratic equation.
Example 1: Write down the intercept form and find out the x-intercepts of the following quadratic functions:
- $y = x^{2} – 4$
- $y = 3x^{2} + 7x – 6$
- $y = 5x^{2} + 3x – 2$
- $y = 6x^{2} + 8x + 2$
Solution:
1).
$y = x^{2} – 4$
$y = (x + 2) (x – 2)$ (1)
We know that the standard intercept form or the factored form is given as:
$y = a (x-p) (x-q)$
Comparing this to equation (1):
$p = -2$ and $q = 2$
Hence, x-intercepts of the given quadratic function are “$(-2, 0)$” and “$(2,0)$”.
2).
$y = 3x^{2} + 7x – 6$
$y = 3x^{2} + 9x – 2x – 6$
$y = 3x (x + 3) – 2 (x + 3)$
$y = (3x – 2) (x + 3)$
$y = 3 (x – \dfrac{2}{3}) (x + 3)$
$p = \dfrac{2}{3}$ and $q = -3$
Hence, x-intercepts of the given quadratic function are “$(\dfrac{2}{3},0)$” and “$(-3,0)$”.
3).
$y = 5x^{2} + 3x – 2$
$y = 5x^{2} + 5x – 2x – 2$
$y = 5x (x + 1) – 2 (x + 1)$
$y = (5x – 2) (x + 1)$
$y = 5(x – \dfrac{2}{5}) (x + 1)$
$p = \dfrac{2}{5}$ and $q = -1$
Hence, x-intercepts of the given quadratic function are “$(\dfrac{2}{5},0)$” and “$(-1,0)$”.
4).
$y = 6x^{2} + 8x + 2$
$y = 6x^{2} + 6x + 2x + 2$
$y = 6x (x + 1) + 2 (x + 1)$
$y = (x + 1) (6x + 2)$
$y = 6 ( x + \dfrac{1}{3}) (x+1)$
$p = -\dfrac{1}{3}$ and $q = -1$
Hence, x-intercepts of the given quadratic function are “$ (-\dfrac{1}{3},0)$” and “$(-1,0)$”.
Example 2: Calculate the axis of symmetry by using the intercept form of the given quadratic equations. Also, draw the complete graph of the parabola.
- $y = x^{2} – 16$
- $y = 9x^{2} + 12x – 5$
- $y = 7x^{2} + 16x + 4$
Solution:
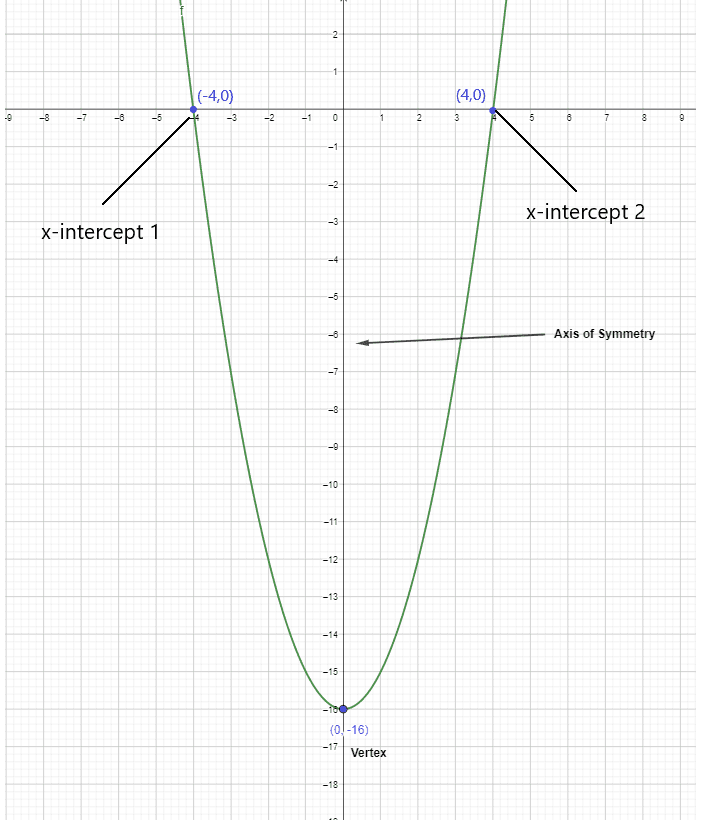
1).
$y = x^{2} – 16$
$y = (x + 4) (x – 4)$
$p = -4$ and $q = 4$
We know the formula for a symmetrical axis is:
$x = \dfrac{p+q}{2}$
$x = \dfrac{4 – 4}{2} = \dfrac{4 – 4}{2} = 0$
Hence, in this case, the axis of symmetry will be the y-axis. We can calculate the vertex through intercept form quadratic vertex/ vertex form quadratic $y = a (x-h)^{2} + k $. Instead of using the vertex form, we will use the axis of symmetry and just put in the original equation and calculate the value of “y”, and this will give us the coordinate of the vertex of the given function.
So the vertex of the parabola is $(0,-16)$, and the graph of the equation can be drawn as:
2).
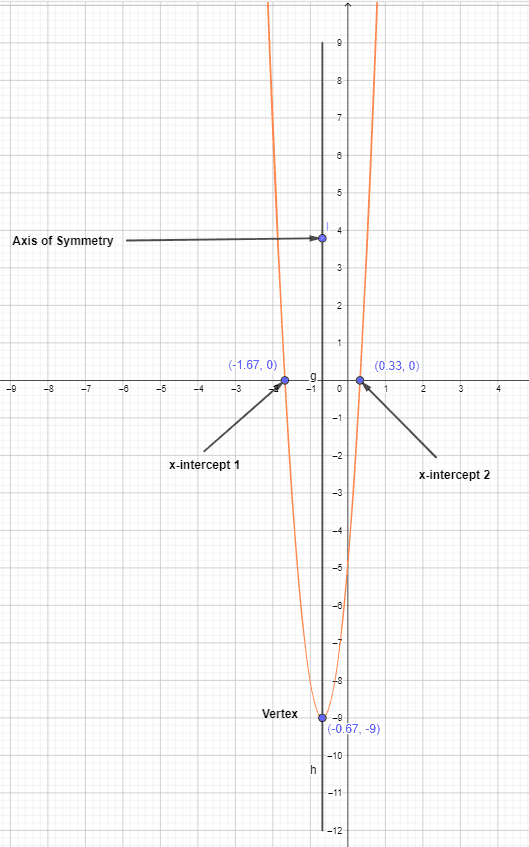
$y = 9x^{2} + 12x – 5$
$y = 9x^{2} + 15x – 3x – 5$
$y = 9x^{2}- 3x +15x – 5$
$y = 3x (x – 1) + 5 (3x – 1)$
$y = (3x + 5) (3x – 1)$
$y = 3 (x + \dfrac{5}{3}) 3 (x – \dfrac{1}{3})$
$y = 9 (x + \dfrac{5}{3}) (x – \dfrac{1}{3})$
$p = – \dfrac{5}{3}$ and $q = \dfrac{1}{3}$
$x = \dfrac{-\dfrac{5}{3} + \dfrac{1}{3} }{2}$
$x = \dfrac{-\dfrac{4}{3}}{2} = -\dfrac{2}{3} $.
Hence, the axis of symmetry is at $x = -\dfrac{2}{3}$.
We will put this value of x in the original equation to get the value of y.
$y = 9 (-\dfrac{2}{3})^{2} + 12(-\dfrac{2}{3}) – 5$
$y = 9 (\dfrac{4}{9}) – 4 – 5$
$y = 4 – 8 -5 = -9$
So the vertex of the parabola is $(-\dfrac{2}{3}, -9)$, and the graph of the equation can be drawn as:
3).
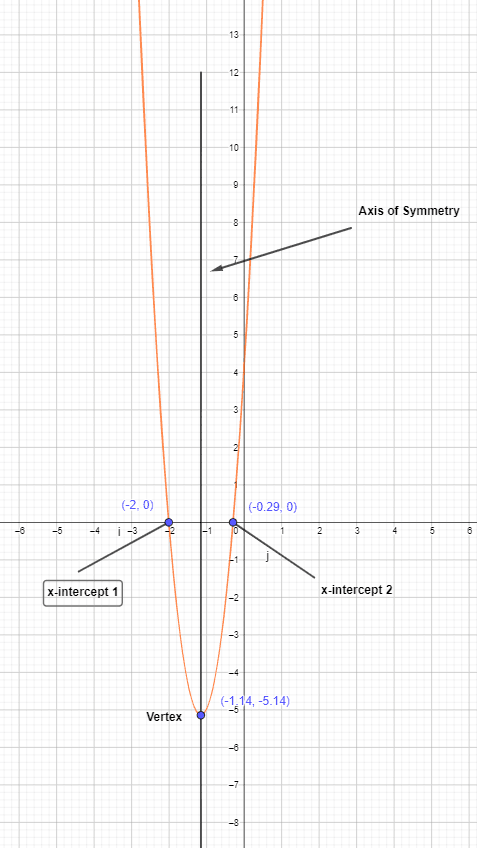
$y = 7x^{2} + 16x + 4$
$y = 7x^{2} + 14x + 2x + 4$
$y = 7x (x + 2) + 2 (x +2)$
$y = (7x + 2) (x + 2)$
$y = 7 (x + \dfrac{2}{7}) (x + 2)$
$p = – \dfrac{2}{7}$ and $q = -2$
$x = \dfrac{-\dfrac{2}{7} – 2 }{2}$
$x = \dfrac{-\dfrac{16}{7}}{2} = -\dfrac{8}{7}$ .
Hence, the axis of symmetry is at $x = -\dfrac{8}{7}$.
We will put this value of x in the original equation to get the value of y.
$y = 7 (-\dfrac{8}{7})^{2} + 16 (-\dfrac{8}{7}) + 4$
$y = 7 (\dfrac{64}{49}) – (\dfrac{128}{7}) + 4$
$y = (\dfrac{64}{7}) – (\dfrac{128}{7}) + 4$
$y = \dfrac{64 – 128 + 28}{7} = -\dfrac{36}{7}$
So the vertex of the parabola is $(-\dfrac{8}{7}, -\dfrac{36}{7})$, and we can draw the graph of the equation as:
Practice Questions
- Calculate the x-intercept and y-intercept for equation $y = 6x^{2} + x – 1$.
- Find out the intercept form of the quadratic equation $y = x^{2}- 6x + 9$ and draw the graph by using the intercept form.
Answer Key:
1).
$y = 6x^{2} + x – 1$
$y = 6x^{2} + 3x – 2x – 1$
$y = 6x (x + \dfrac{1}{2}) – 2 (x + \dfrac{1}{2})$
$y = (6x – 2) (x + \dfrac{1}{2})$
$y = 6 (x – \dfrac{1}{3}) (x + \dfrac{1}{2})$
$p = \dfrac{1}{3}$ and $q = -\dfrac{1}{2}$
Hence, x-intercepts of the given quadratic functions are “$\dfrac{1}{3}$” and “$-\dfrac{1}{2}$”.
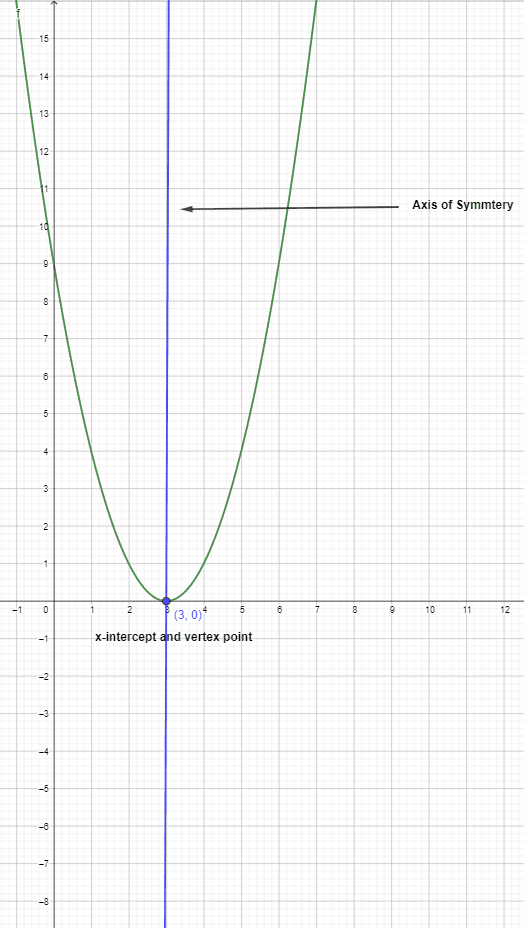
2).
$y = x^{2} – 6x + 9$
$y = x^{2} – 3x – 3x + 9$
$y = x (x – 3) – 3 (x – 3)$
$y = (x – 3) (x – 3)$
So in this case, the x-intercept is the same, and we have only one x-intercept, which is $x = 3$. If we put this value back in the equation, we get $y = 0$, so the x-intercept is $(3,0)$.
Axis of symmetry = $\dfrac{(3 + 3)}{2} = 3$
$y = 3^{2}-6 (3) + 9 = 0$
So the vertex of the parabola is $(3,0)$, and it is the same as the x-intercept, so whenever a quadratic equation has only one intercept, it will also be the vertex of the equation as well.