JUMP TO TOPIC

This article aims to dive deep into monotonic sequences, demystifying their concept, properties, and significance in mathematical theory and its practical applications. Whether you’re a mathematics enthusiast or a curious learner, this exploration of monotonic sequences promises to enrich your understanding and appreciation of this intricate mathematical construct.
Defining Monotonic Sequence
In mathematics, a sequence is monotonic if its elements follow a consistent trend — either increasing or decreasing. More specifically, a sequence is:
Monotonically increasing (or non-decreasing) if every term is greater than or equal to the one before. Formally, a sequence {a_n} is monotonically increasing if, for all n, a_n ≤ a_n+1.
Monotonically decreasing (or non-increasing) if every term is less than or equal to the one before. Formally, a sequence {a_n} is monotonically decreasing if, for all n, a_n ≥ a_n+1.
Note that in both cases, the inequality can be strict (e.g., a_n < a_n+1 or a_n > a_n+1) or non-strict (e.g., a_n ≤ a_n+1 or a_n ≥ a_n+1), leading to strictly increasing/decreasing or non-strictly increasing/decreasing sequences respectively.
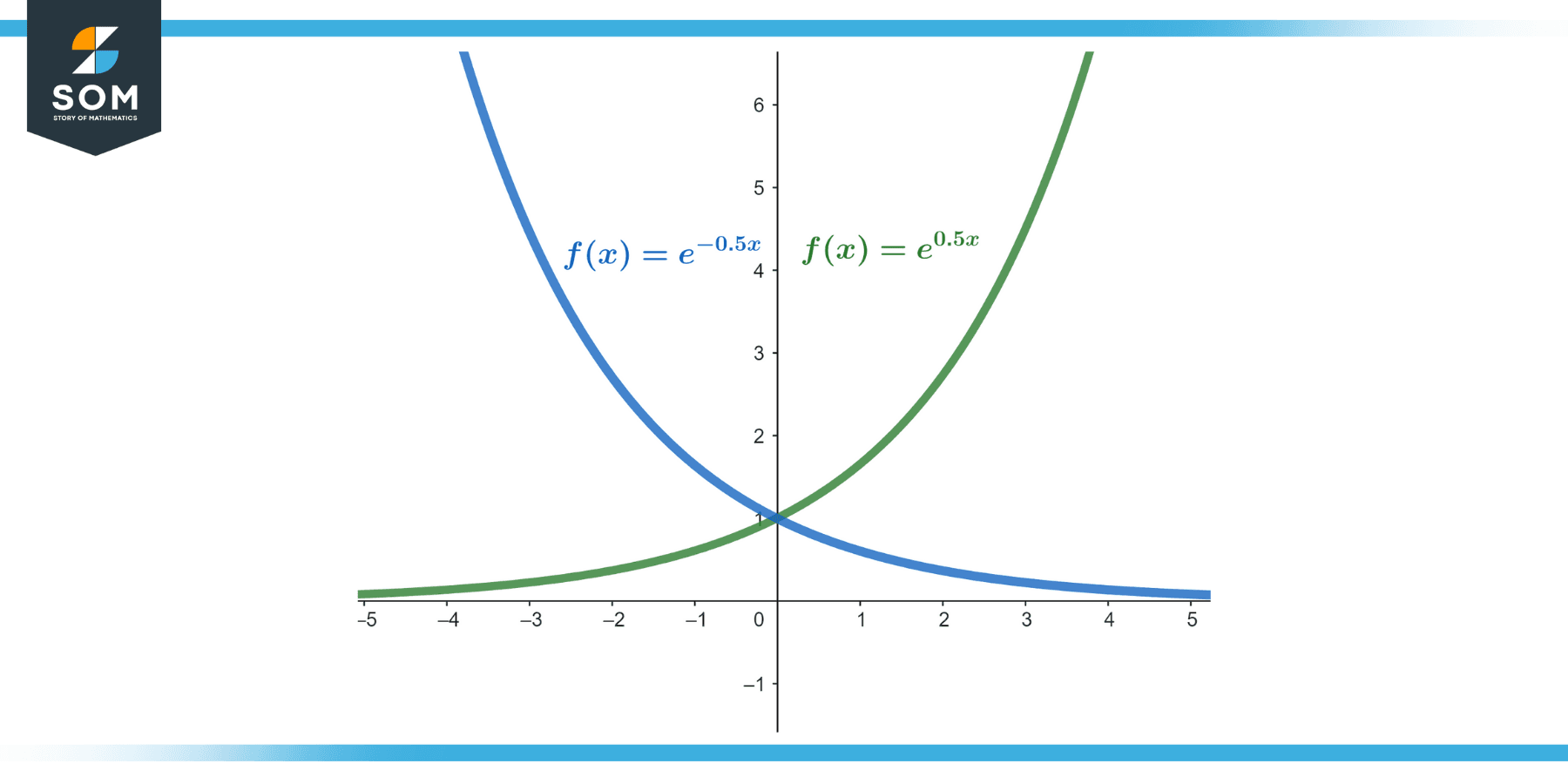
Figure-1.
Properties of Monotonic Sequence
Monotonic sequences have several important properties that are frequently used in mathematical analysis. Here are some of the key properties:
Boundedness
A monotonic sequence is said to be bounded if there is a limit to its values. More specifically, a sequence is bounded above if there is a number M such that no term in the sequence is greater than M. Likewise, it’s bounded below if there’s a number m such that no term in the sequence is less than m.
An important theorem in real analysis, the Monotone Convergence Theorem, states that every bounded, monotonic sequence must converge to a limit. This means that if a sequence is increasing and bounded above or decreasing and bounded below, it will have a finite limit.
Convergence or Divergence
As mentioned above, if a monotonic sequence is bounded, it must converge to a limit. However, it diverges to positive or negative infinity if it is not bounded. For example, the sequence {n} where n = 1, 2, 3, … is monotonically increasing and unbounded; hence, it diverges to positive infinity.
Subsequences
Any subsequence of a monotonic sequence is also a monotonic sequence. In other words, if you take elements from a monotonic sequence while preserving the original order, the resulting sequence will also be monotonic.
Combining Monotonic Sequences
If two sequences are both monotonically increasing or both monotonically decreasing, their sum, difference, and product will also be monotonic in the same direction, provided the sequences are not alternating around zero.
Infinite Subsequences
If a sequence is not monotonic, it still contains an infinite subsequence which is monotonic. This is a consequence of the Bolzano–Weierstrass theorem, which states that every bounded sequence contains a convergent subsequence. Since convergent subsequences must be monotonic, every sequence contains a monotonic subsequence.
Limits of Functions
If a function is monotonically increasing or decreasing over an interval and is bounded, then the function has limits at the endpoints of the interval. This is a useful property when determining the limits of functions.
Remember, these properties form the backbone of many proofs and concepts in real analysis and calculus. They help to understand the behavior of sequences and functions, leading to further understanding of more complex mathematical ideas.
Exercise
Example 1
State the status of the following sequence: {n}, for n ∈ {1, 2, 3, …}
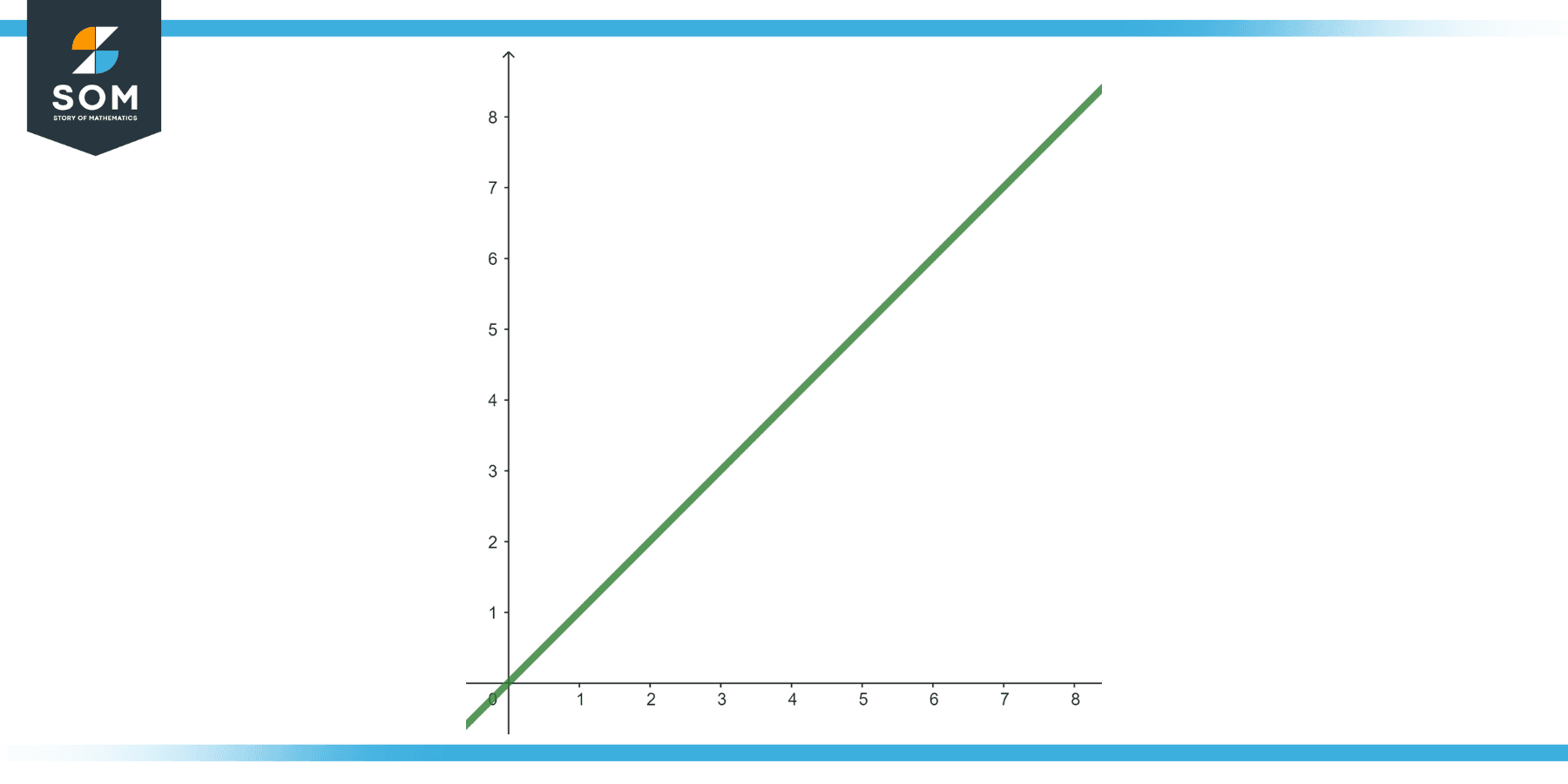
Figure-2.
Solution
The sequence {n} for n ∈ {1, 2, 3, …} is monotonically increasing. Each term is simply one more than the previous term.
Example 2
State the status of the following sequence: {1/n} for n ∈ {1, 2, 3, …}.
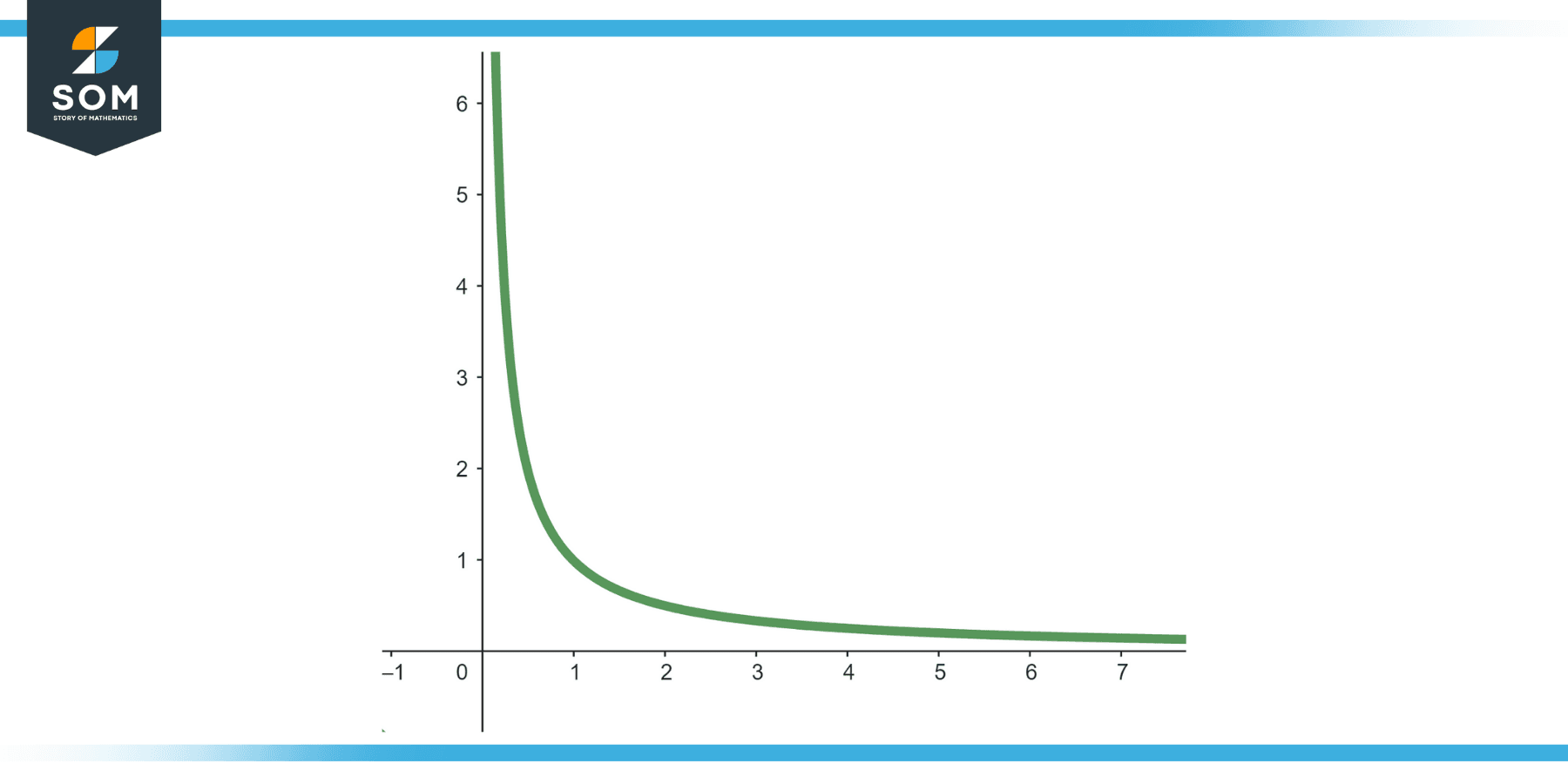
Figure-3.
Solution
The sequence {1/n} for n ∈ {1, 2, 3, …} is a monotonically decreasing sequence. As n increases, 1/n gets smaller and smaller.
Example 3
State the status of the following sequence: {(-1)ⁿ/n} for n ∈ {1, 2, 3, …}
Solution
The sequence {(-1)ⁿ/n} for n ∈ {1, 2, 3, …}, is a monotonically decreasing sequence. Despite the (-1)ⁿ, which alternates sign, the division by n makes each term smaller in magnitude than the last.
Example 4
State the status of the following sequence: {2ⁿ} for n ∈ {1, 2, 3, …}.
Solution
The sequence {2ⁿ} for n ∈ {1, 2, 3, …} is a monotonically increasing sequence. Each term is double the previous term.
Example 5
State the status of the following sequence: {1 – 1/n} for n ∈ {1, 2, 3, …}.
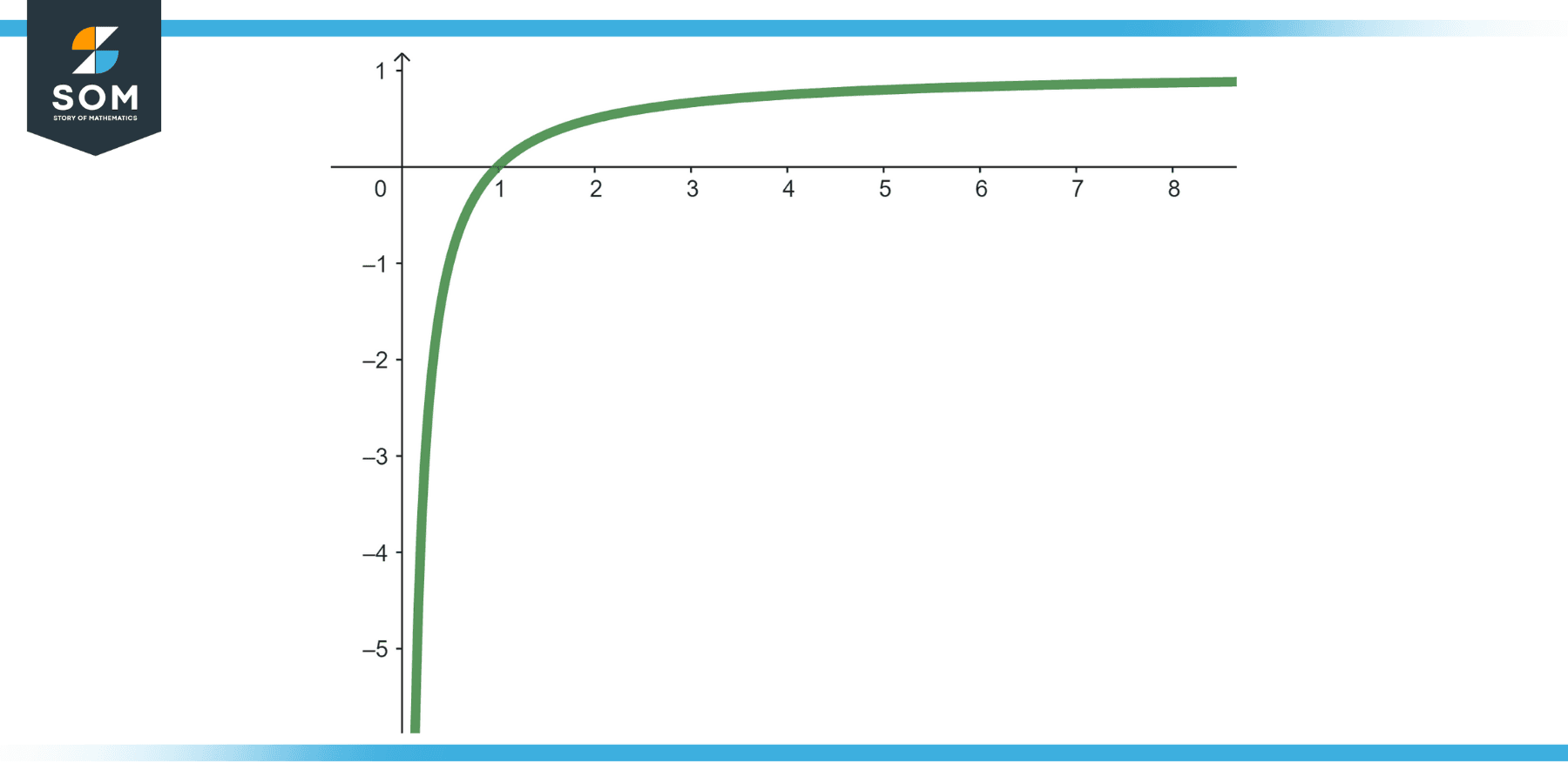
Figure-4.
Solution
The sequence {1 – 1/n} for n ∈ {1, 2, 3, …} is monotonically increasing. As n increases, 1/n decreases; thus, 1 – 1/n increases.
Example 6
State the status of the following sequence: {n/(n+1)} for n ∈ {1, 2, 3, …}.
Solution
The sequence {n/(n+1)} for n ∈ {1, 2, 3, …}, is a monotonically increasing sequence. As n increases, the ratio n/(n+1) also increases, although it will never reach 1.
Example 7
State the status of the following sequence: {√n} for n ∈ {1, 2, 3, …}.
Solution
The sequence {√n} for n ∈ {1, 2, 3, …} is monotonically increasing. The square root function is increasing for positive n.
Example 8
State the status of the following sequence: {(-1)ⁿ * n} for n ∈ {1, 2, 3, …}.
Solution
The sequence {(-1)ⁿ * n} for n ∈ {1, 2, 3, …}, is not monotonic. Here the terms alternate between positive and negative and increase in magnitude, so neither the increasing nor the decreasing condition is satisfied for all n.
But, we can consider the subsequences where n is even, and n is odd separately. The subsequence {(-1)ⁿ * n} for n ∈ {1, 3, 5, …} is monotonically decreasing and the subsequence {(-1)ⁿ * n} for n ∈ {2, 4, 6, …} is monotonically increasing.
Applications
Monotonic sequences find various applications in various fields due to their defined order and pattern. Here are a few notable examples:
Mathematics
In mathematics, monotonic sequences are used in proofs and theorems involving limits, continuity, differentiability, and integrability. For instance, the Monotone Convergence Theorem uses monotonic sequences to assert that every bounded monotonic sequence converges. Moreover, monotonic functions and their properties in real analysis often make problems more tractable.
Computer Science
Monotonic sequences play a significant role in computer science, particularly in algorithms and data structures. For instance, Longest Increasing Subsequence (LIS) problems are a classic application where monotonic sequences come into play. Additionally, monotonicity properties can help in optimization problems and the design of efficient algorithms.
Economics and Finance
Monotonic sequences can model certain types of economic or financial behavior. For instance, a company’s cumulative profit or revenue over time would typically be modeled as a monotonically increasing sequence. Additionally, in utility theory, the concept of monotonic preferences assumes that more of a good or service is always better, leading to a monotonically increasing utility function.
Physics and Engineering
In physics and engineering, monotonic sequences can be used to model processes with a clear progression direction. For instance, the decay of a radioactive substance, or the charging or discharging of a capacitor in an electrical circuit, can be modeled using monotonic sequences.
Ecology and Environmental Science
Monotonic sequences can model population growth under certain conditions or the accumulation of pollutants in an ecosystem.
Statistics and Machine Learning
In statistical inference and machine learning, certain types of regression analysis, like isotonic regression, seek to find the best-fit monotonically increasing or decreasing function for a given data set. Monotonicity constraints are also crucial in certain machine-learning algorithms to ensure consistent behavior.
Generally, whenever a quantity is observed to increase or decrease over time or across conditions consistently, a monotonic sequence or function can be useful for describing and analyzing that process.
Historical Significance
While seemingly simple, the concept of a monotonic sequence is an integral part of calculus and real analysis, and its development is intertwined with the history of these fields.
The concept of a sequence, which is foundational to a monotonic sequence, is ancient. The ancient Greeks, for instance, were aware of sequences like arithmetic and geometric progressions. However, the study of sequences in a formal mathematical sense began to take shape during the 17th century with the advent of calculus by mathematicians like Isaac Newton and Gottfried Wilhelm Leibniz.
However, the concept of monotonicity as we understand it today was developed much later in the 19th century with the rigorous formulation of calculus and real analysis. This was a period when mathematicians were trying to lay down solid foundations for calculus, which led to the development of mathematical analysis.
Augustin-Louis Cauchy, a French mathematician, was one of the pioneers in this regard. He introduced rigorous definitions and proofs in calculus and made substantial contributions to the theory of functions, sequences, and series. The concept of a limit, central to the idea of a monotonic sequence, owes much to his work.
The Monotone Convergence Theorem, a pivotal theorem involving monotonic sequences, was developed as part of this endeavor to provide solid underpinnings to calculus. This theorem states that every bounded monotonic sequence is convergent and is a fundamental result in real analysis.
All images were created with GeoGebra.
