
This article will delve into the fascinating world of u-substitution in definite integrals, aiming to provide readers with a comprehensive understanding of its concept, application, and significance. We’ll unravel its intricacies, explore its properties, and demonstrate its utility with practical examples, offering a holistic view of this vital calculus tool.
Definition of U Substitution Definite Integral
In calculus, u-substitution is a method for finding integrals. In u-substitution, the substitution u = g(x) is made to simplify the integral. When a definite integral is considered, the limits of the integral are also changed according to the new variable ‘u.’
More formally, if you have an integral of form ∫f(g(x)) * g'(x) dx, you can make a substitution to simplify this to ∫f(u) du, where u is a function u = g(x). The corresponding limits of the integral in terms of ‘u‘ are found by substituting the original ‘x‘ limits into the function u = g(x).
U-substitution, essentially the reverse process of the chain rule of differentiation, can greatly simplify finding many integrals.
Example
∫x² √(x³ + 1) dx; [0 to 2]
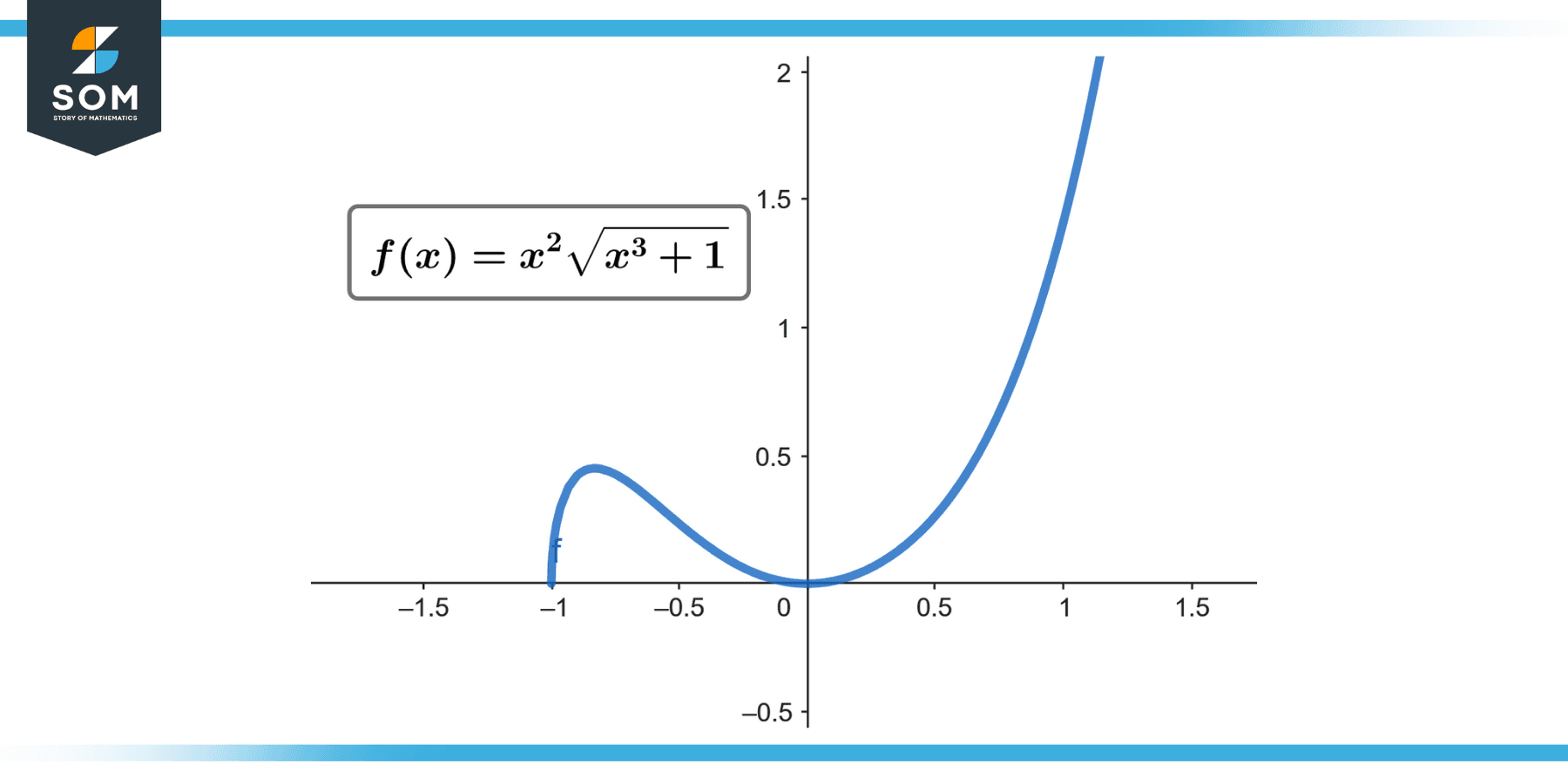
Figure-1.
Solution
Let u = x³ + 1 du = 3x² dx
Substitute the limits: When x = 0, u = 0³ + 1 = 1 When x = 2, u = 2³ + 1 = 9
The integral becomes:
∫(1/3)√u du, [1 to 9]
Applying power rule and u-substitution:
= (1/3) * (2/3) * (u³∕²)) evaluated from 1 to 9
= (2/9) * (9√9 – 1√1)
= (2/9) * (27 – 1)
= (2/9) * 26
= 52/9
Therefore, ∫[0 to 2] x² √(x³ + 1) dx = 52/9
Evaluation Process
The evaluation process of u-substitution in definite integrals involves several steps, as outlined below:
Identify a Substitution
Start by identifying a part of the integral that could simplify the problem if substituted with a single variable, ‘u.’ Typically, you’d select a function that makes the integral look simpler when substituted or a function whose derivative is present elsewhere in the integral.
Make the Substitution
Replace the chosen part of the function with ‘u‘. So, if you have a function of the form ∫f(g(x)) * g'(x) dx, you substitute u = g(x), so the integral becomes ∫f(u) * du.
Change the Limits of Integration
For definite integrals, remember to change the limits of integration. If the original limits of the x-integral are a and b, then substitute these into your equation u = g(x) to find the new limits for u. Let’s say these are c and d.
Perform the Integral with the New Variable
With a simpler function and limits, perform the integration in terms of ‘u‘. This will yield a new function, let’s call it F(u).
Substitute ‘u’ Back In
Replace ‘u‘ with the original function g(x) in the antiderivative. Now we have a new function F(g(x)).
Evaluate Between the New Limits
Finally, substitute the new limits (in terms of ‘u‘) into the antiderivative, calculate the difference, and get the final result. That is, you’ll be finding F(d) – F(c).
Exercise
Example 1
∫(3x² + 2x + 1) $e^{(x³ + x² + x)}$ dx; [-1 to 1]
Solution
Let u = x³ + x² + x du = (3x² + 2x + 1) dx
Substitute the limits: When x = -1, u = (-1)³ + (-1)² + (-1) = -1 When x = 1, u = 1³ + 1² + 1 = 3
The integral becomes:
∫eᵘ du; [-1 to 3]
Applying the power rule and u-substitution:
= eᵘ evaluated from -1 to 3 = e³ – e⁻¹
Therefore:
∫(3x² + 2x + 1) $e^{(x³ + x² + x)}$ dx; [-1 to 1]
= e³ – e⁻¹
Example 2
∫x³ √(x⁴ – 1) dx; [1 to 2]
Solution
Let u = x⁴ – 1 du = 4x³ dx
Substitute the limits: When x = 1, u = 1⁴ – 1 = 0 When x = 2, u = 2⁴ – 1 = 15
The integral becomes:
∫(1/4) √u du; [0 to 15]
Applying power rule and u-substitution:
= (1/4) * (2/3) * (u³∕²) evaluated from 0 to 15
= (1/4) * (2/3) * (15³∕² – 0³∕²)
= (1/4) * (2/3) * (15³∕²)
= (1/6) * (15³∕²)
Therefore:
∫x³ √(x⁴ – 1) dx; [1 to 2]
= (1/6) * (15³∕²)
Example 3
∫sin(2θ) cos²(θ) dθ; [-π/2 to π/2]
Solution
Let u = cos(θ) du = -sin(θ) dθ
Substitute the limits: When θ = -π/2, u = cos(-π/2) = 0 When θ = π/2, u = cos(π/2) = 0
The integral becomes:
∫-u² du; [0 to 0]
Since the limits are the same, the integral evaluates to 0.
Therefore:
∫sin(2θ) cos²(θ) dθ; [-π/2 to π/2]
= 0
Example 4
∫(x² – 2x + 1) √(1 – x²) dx; [-1 to 1]
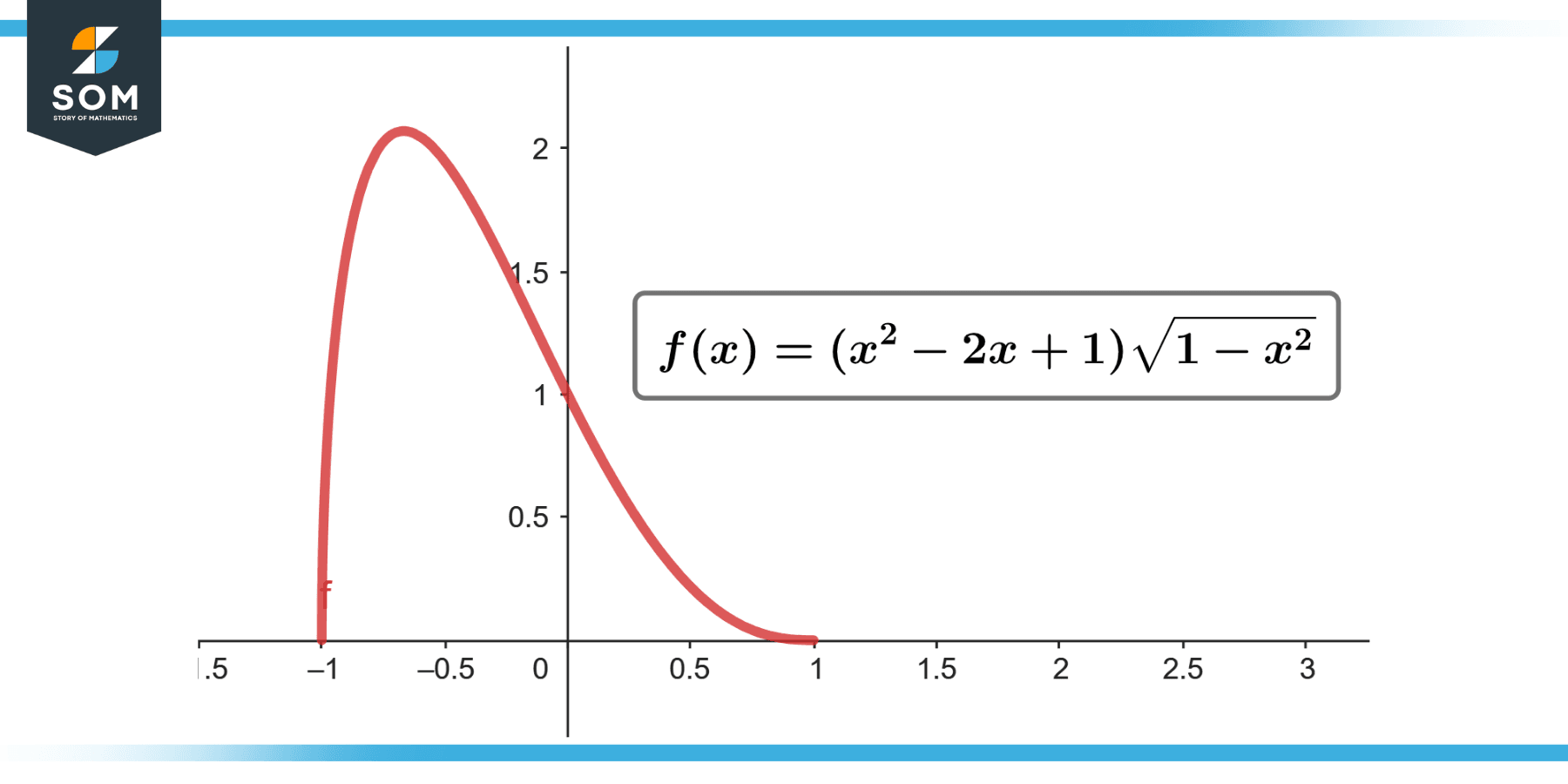
Figure-2.
Solution
Let u = 1 – x² du = -2x dx
Substitute the limits: When x = -1, u = 1 – (-1)² = 0 When x = 1, u = 1 – 1² = 0
The integral becomes:
∫-(1/2) √u du; [0 to 0]
Since the limits are the same, the integral evaluates to 0.
Therefore:
∫(x² – 2x + 1) √(1 – x²) dx; [-1 to 1]
= 0
Example 5
∫x³ $e^{(x⁴)}$ dx; [0 to 1]
Solution
Let u = x⁴ du = 4x³ dx
Substitute the limits: When x = 0, u = 0⁴ = 0 When x = 1, u = 1⁴ = 1
The integral becomes:
∫(1/4) eᵘ du; [0 to 1]
= (1/4) * ∫eᵘ du; [0 to 1]
= (1/4) * (e¹ – e⁰)
= (1/4) * (e – 1)
Therefore:
∫x³ $e^{(x⁴)}$ dx = (1/4) * (e – 1); [0 to 1]
Example 6
∫sin³(θ) cos²(θ) dθ; [-π/2 to π/2]
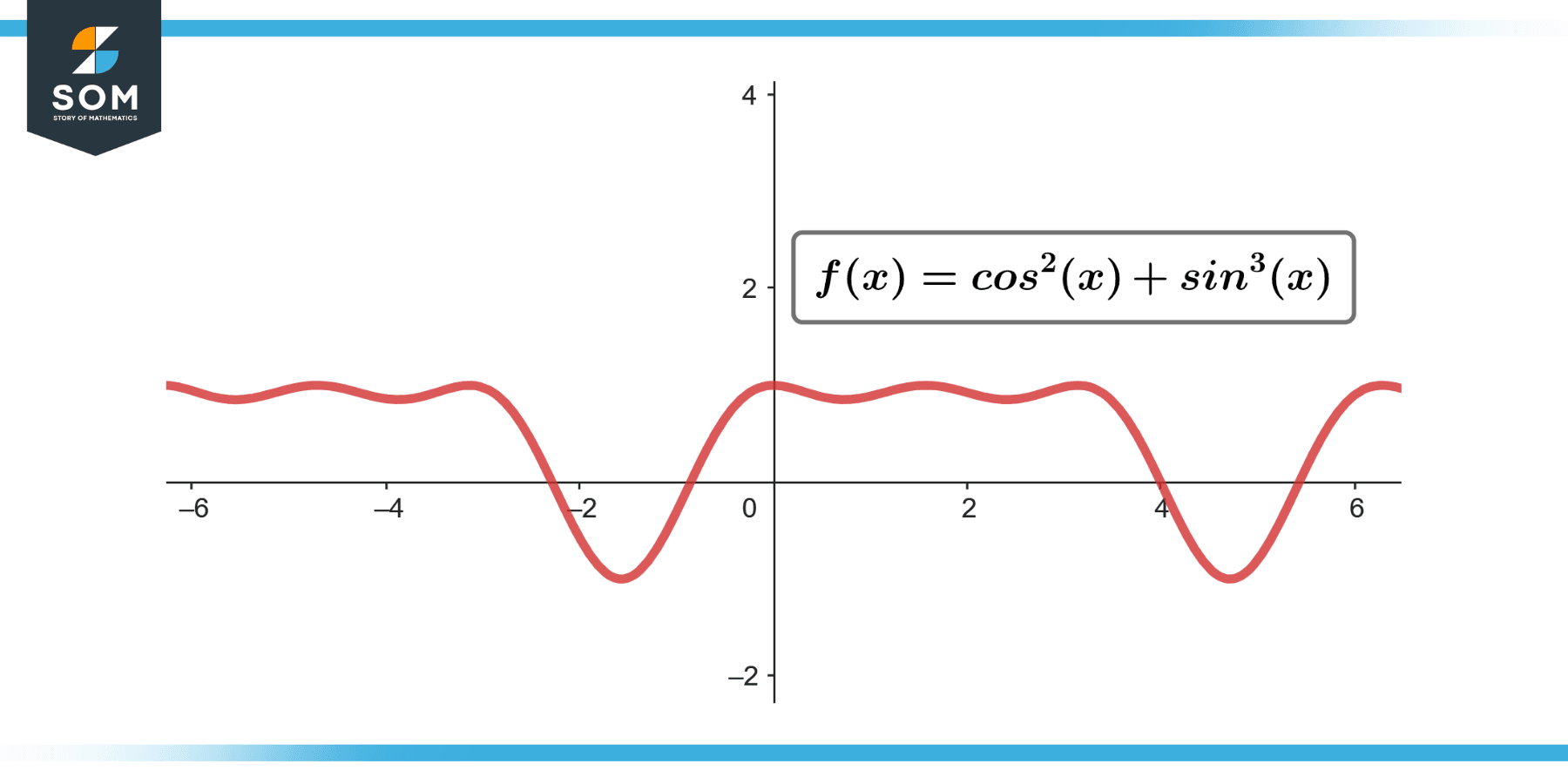
Figure-3.
Solution
Let u = cos(θ) du = -sin(θ) dθ
Substitute the limits: When θ = -π/2, u = cos(-π/2) = 0 When θ = π/2, u = cos(π/2) = 0
The integral becomes:
∫-u² (1 – u²) du; [0 to 0]
Since the limits are the same, the integral evaluates to 0.
Therefore:
∫sin³(θ) cos²(θ) dθ = 0; [-π/2 to π/2]
Applications
The concept of u-substitution in definite integrals is fundamental to calculus and thus finds extensive applications across multiple disciplines that use calculus in their work. Here are a few of those applications:
Physics
In physics, integration, including u-substitution, is used to calculate quantities like work done by a variable force, electric and magnetic fields created by charge and current distributions, or the moment of inertia of an object with a complex shape.
Engineering
In many engineering problems, especially those involving calculus of variations, u-substitution simplifies the integrals. It is frequently used in electrical engineering, where integration is used to calculate quantities like charge, energy, power, etc., given their rates.
Economics
In economics, integration is used in numerous ways, such as determining consumer and producer surplus, calculating the present value of a continuous income stream, or modeling and solving dynamic equilibrium problems. The method of u-substitution often simplifies these calculations.
Statistics and Probability
U-substitution is often used for probability density functions, especially continuous random variables. It is also used in the process of normalization, where a probability density function is made to integrate to 1.
Biology
In biology, integrals, including those simplified by u-substitution, are used in growth and decay models, population dynamics, and in interpreting the behavior of systems over continuous intervals.
Computer Graphics
In the field of computer graphics, and particularly in rendering and animation, integrals are used to calculate light and color values in a scene. U-substitution is often used to simplify these integrals, making them computationally more efficient.
Medicine
In biomedical engineering, the u-substitution method is often used in signal and image processing applications, such as modeling the response of a biological system to a drug dosage over time.
Environmental Sciences
In studying pollutant spread or population dynamics of certain species, the u-substitution method in definite integrals can be employed to model and predict behaviors over time.
Chemistry
In physical chemistry, integration using u-substitution is used for solving differential equations related to reaction rates. It’s also used in quantum mechanics to calculate probabilities from wave functions.
Geography and Meteorology
U-substitution in integrals can be used in models predicting weather patterns and climate change, as these often involve calculations of accumulated changes over time or space.
Astronomy and Space Science
Integration calculates various physical quantities, such as gravitational and electromagnetic fields, often involving complex or spherical coordinates where u-substitution can simplify the integrals.
Operations Research
This field often requires the optimization of certain resources. The associated problems frequently involve integration, where u-substitution can be used to simplify complex relationships.
Machine Learning and Data Science
Integration is fundamental to machine learning and data science aspects, like calculating areas under the ROC curve, probability densities, and more. U-substitution is a helpful tool in solving these integrals.
Psychophysics
In the field of psychophysics, which investigates the relationship between stimuli (which are physical) and the sensations and perceptions they affect (which are psychological), definite integrals using u-substitution are often used to quantify the relationship between the physical stimulus and the perceived sensation.
Finance and Actuarial Science
Integration techniques, including u-substitution, are used in calculating the present and future values of continuous income streams, pricing complex financial derivatives, and building models in actuarial science.
All images were created with GeoGebra and MATLAB.
