JUMP TO TOPIC

This article aims to elucidate the principles of scalar and vector projections, underscoring their importance and how these concepts provide vital tools for understanding multidimensional spaces.
We will delve into their mathematical underpinnings, explore the differences between scalar and vector projections, and illustrate their real-world implications through various examples.
Defining Scalar and Vector Projections
In mathematics, scalar and vector projections help to understand the position of a point in space in relation to other points. Let’s break down the definitions of each.
Scalar Projection
The scalar projection (or scalar component) of a vector A onto a vector B, also known as the dot product of A and B, represents the magnitude of A that is in the direction of B. Essentially, it is the length of the segment of A that lies on the line in the direction of B. It is calculated as |A|cos(θ), where |A| is the magnitude of A and θ is the angle between A and B.
Below, we present a generic example of scalar projection in figure-1.
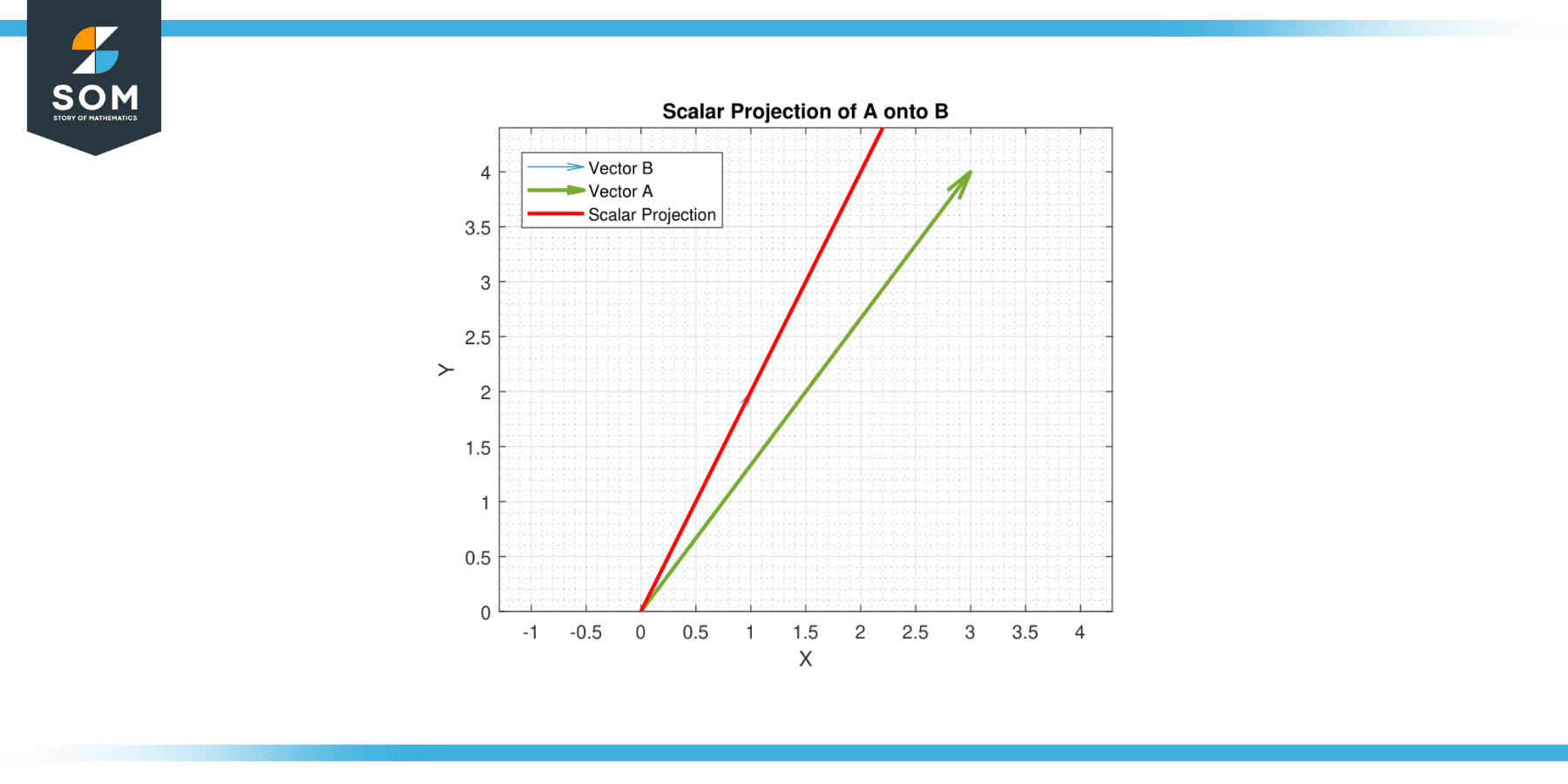
Figure-1.
Vector Projection
The vector projection of a vector A onto a vector B, sometimes denoted as proj_BA, represents a vector that is in the direction of B with a magnitude equal to the scalar projection of A onto B.
Essentially, it is the vector ‘shadow’ of A when ‘light’ is shone from B. It is calculated as (A·B/|B|²) * B, where · is the dot product, and |B| is the magnitude of B. Below, we present a generic example of vector projection in figure-2.
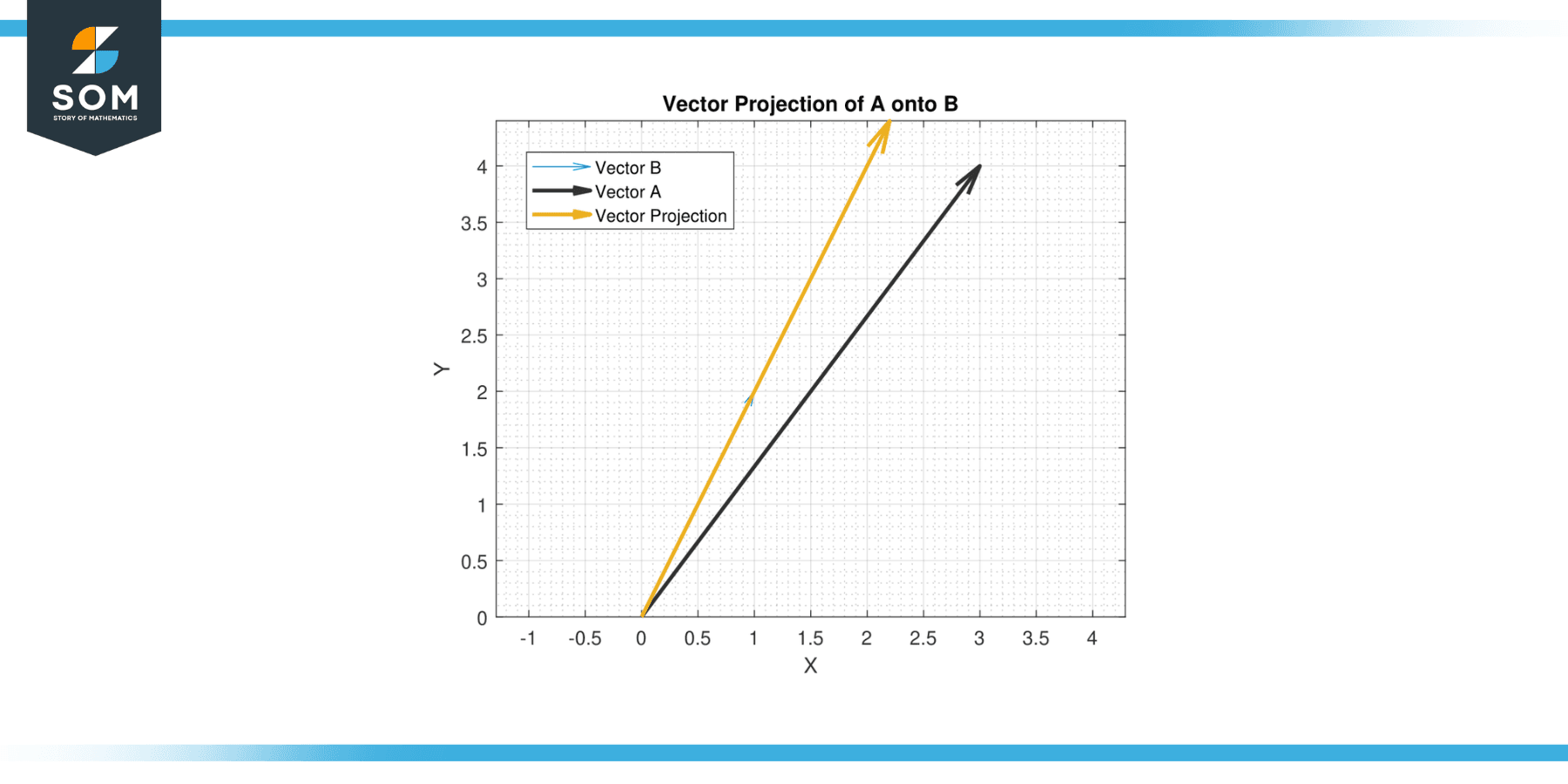
Figure-2.
Properties
Scalar Projection
Commutative Property
The scalar projection of vector A onto vector B is the same as the scalar projection of vector B onto vector A when the vectors are nonzero. This is because the dot product, which is used to calculate the scalar projection, is commutative.
Scalability
Scalar projection is directly proportional to the magnitude of the vectors. If the magnitude of either vector is scaled by a factor, the scalar projection scales by the same factor.
Directionality
The sign of the scalar projection gives information about the direction. A positive scalar projection means vectors A and B are in the same direction. A negative scalar projection indicates they are in opposite directions. A zero scalar projection means the vectors are perpendicular.
Cosine Relationship
The scalar projection is tied to the cosine of the angle between the two vectors. As a result, the maximum scalar projection occurs when the vectors are aligned (cosine of 0° is 1), and the minimum when they are opposite (cosine of 180° is -1).
Vector Projection
Non-commutativity
Unlike scalar projections, vector projections are not commutative. The vector projection of A onto B is not the same as the vector projection of B onto A, unless A and B are parallel.
Scalability
If you scale vector B, the vector onto which A is projected, the vector projection will scale by the same factor.
Collinearity
The vector projection of A onto B is collinear with B. In other words, it lies on the same line as B.
Directionality
The vector projection of A onto B always points in the direction of B if B is a non-zero vector. If the scalar projection is negative, the vector projection will still point in the same direction as B, but it would have indicated that A was in the opposite direction.
Orthogonality
The vector formed by subtracting the vector projection of A onto B from A is orthogonal (perpendicular) to B. This is called the orthogonal projection of A onto B and is a fundamental concept in many mathematical fields, especially in linear algebra.
Exercise
Scalar Projections
Example 1
Let A = [3, 4] and B = [1, 2]. Find the scalar projection of A onto B.
Solution
The formula for the scalar projection of A onto B is given by A.B/||B||. The dot product is:
A.B = (3)(1) + (4)(2)
A.B = 11
The magnitude of B is:
||B|| = √(1² + 2²)
||B|| = √5
Hence, the scalar projection of A onto B is 11/√5 = 4.9193.
Example 2
Let A = [5, 0] and B = [0, 5]. Find the scalar projection of A onto B.
Solution
The dot product is given by:
A.B = (5)(0) + (0)(5)
A.B = 0
The magnitude of B is:
||B|| = √(0² + 5²)
||B|| = 5
Hence, the scalar projection of A onto B is 0/5 = 0. Since the vectors are perpendicular, the scalar projection is zero, as expected.
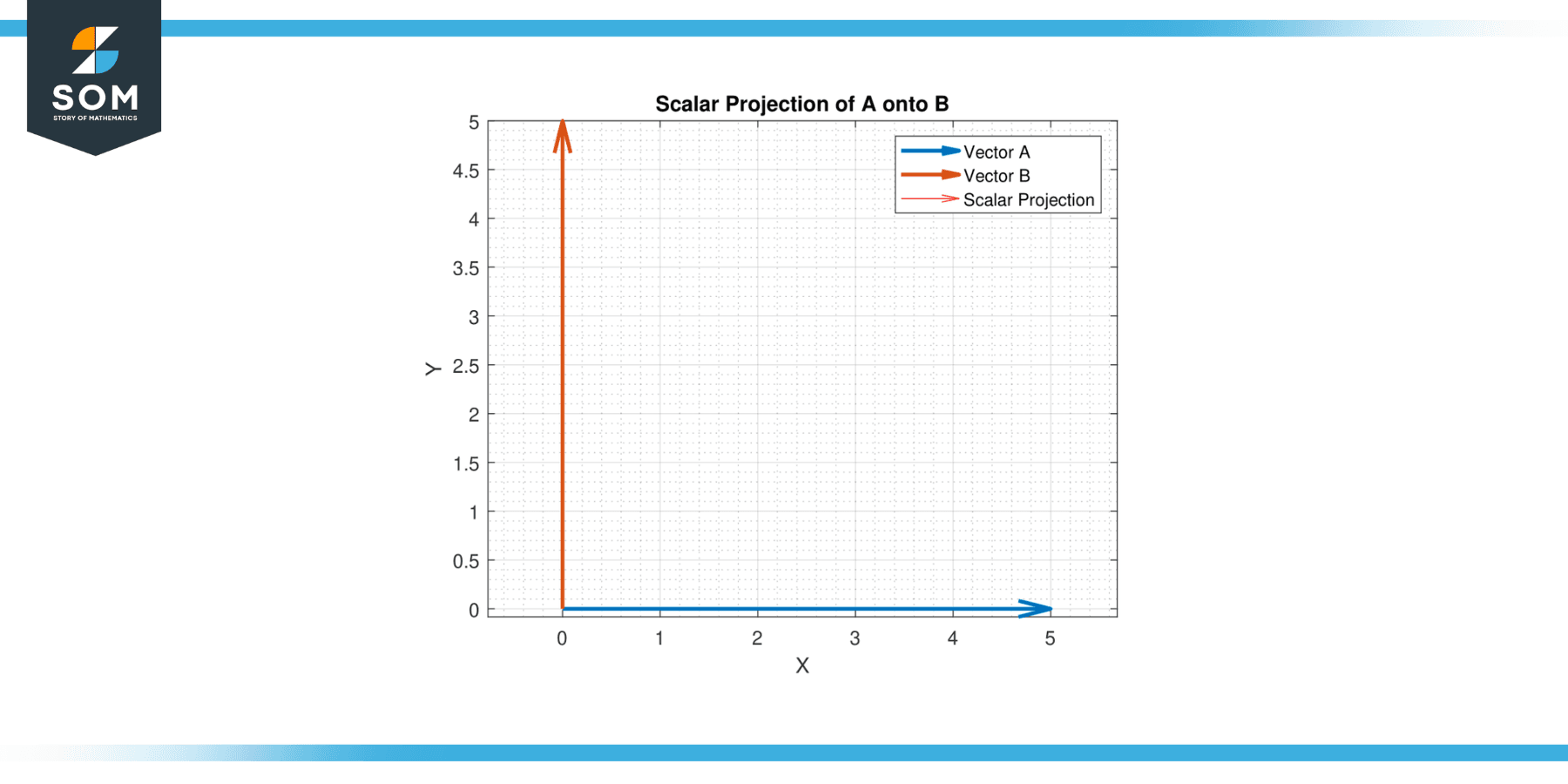
Figure-3.
Example 3
Let A = [-3, 2] and B = [4, -1]. Find the scalar projection of A onto B.
Solution
The dot product is given by:
A.B = (-3)(4) + (2)(-1)
A.B = -14
The magnitude of B is:
||B|| = √(4² + (-1)²)
||B|| = √(17)
Hence, the scalar projection of A onto B is -14/√(17) = -3.392.
Example 4
Let A = [2, 2] and B = [3, -3]. Find the scalar projection of A onto B.
Solution
The dot product is given by:
A.B = (2)(3) + (2)(-3)
A.B = 0
The magnitude of B is:
||B|| = √(3² + (-3)²)
||B|| = √(18)
||B|| = 3 * √2
Hence, the scalar projection of A onto B is 0/(3 * √2) = 0. Again, since the vectors are perpendicular, the scalar projection is zero.
Vector Projections
Example 5
Let A = [1, 2] and B = [3, 4]. Find the vector projection of A onto B.
Solution
The formula for the vector projection of A onto B is given by:
( A·B / ||B||² ) B
The dot product is given by:
A.B = (1)(3) + (2)(4)
A.B = 11
The magnitude of B is:
||B|| = √(3² + 4²)
||B|| = 5
so ||B||² = 25
Hence, the vector projection of A onto B is (11/25) [3, 4] = [1.32, 1.76].
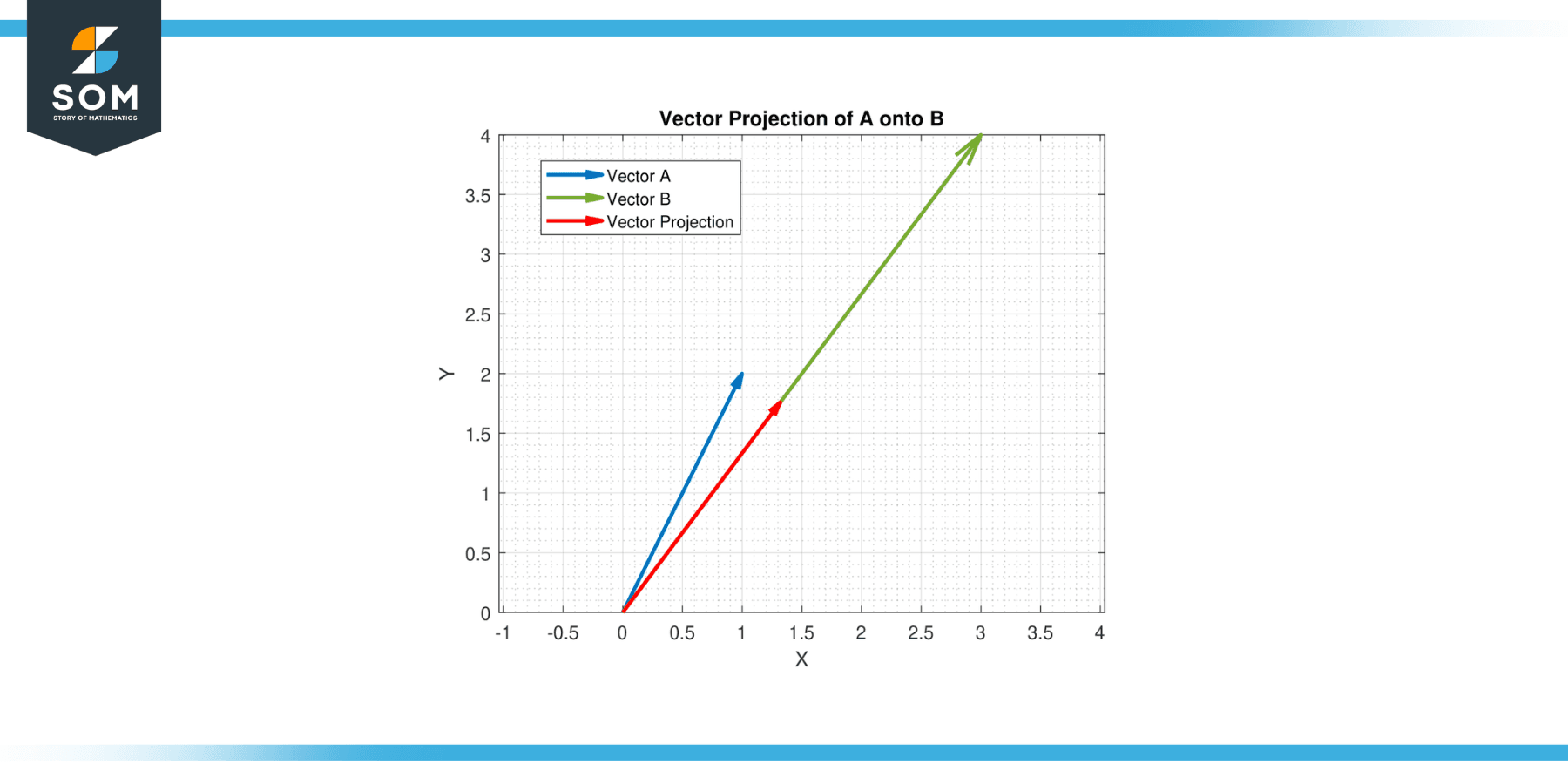
Figure-4.
Example 6
Let A = [5, 0] and B = [0, 5]. Find the vector projection of A onto B.
Solution
The dot product is given by:
A.B = (5)(0) + (0)(5)
A.B = 0
The magnitude of B is :
||B|| = √(0² + 5²)
||B|| = 5
so ||B||^2 = 25
Hence, the vector projection of A onto B is (0/25)[0, 5] = [0, 0]. This result reflects the fact that A and B are orthogonal.
Example 7
Let A = [-3, 2] and B = [4, -1]. Find the vector projection of A onto B.
Solution
The dot product is given by:
A.B = (-3)(4) + (2)(-1)
A.B = -14
The magnitude of B is:
||B|| = √(4² + (-1)²)
||B|| = √17
so ||B||² = 17.
Hence, the vector projection of A onto B is (-14/17)[4, -1] = [-3.29, 0.82].
Example 8
Let A = [2, 2] and B = [3, -3]. Find the vector projection of A onto B.
Solution
The dot product is given by:
A.B = (2)(3) + (2)(-3)
A.B = 0
The magnitude of B is:
||B|| = √(3² + (-3)²)
||B|| = √18
||B|| = 3 * √2
so ||B||² = 18.
Hence, the vector projection of A onto B is (0/18)[3, -3] = [0, 0]. Once again, because A and B are orthogonal, the vector projection is the zero vector.
Applications
Scalar and vector projections have broad applications across a range of fields:
Computer Science
Projections are used in computer graphics and game development. When rendering 3D graphics on a 2D screen, vector projections help to create the illusion of depth. Furthermore, in machine learning, the concept of projection is used in dimensionality reduction techniques like Principal Component Analysis (PCA), which projects data onto lower-dimensional spaces.
Mathematics
In mathematics, and more specifically linear algebra, vector projections are used in various algorithms. For example, the Gram-Schmidt process utilizes vector projections to orthogonally project vectors and create an orthonormal basis. Additionally, vector projections are employed in least squares approximation methods, where they help minimize the orthogonal projection of the error vector.
Computer Vision and Robotics
Vector projections are used in camera calibration, object recognition, and pose estimation. In robotics, projections are utilized to calculate robot movements and manipulations in 3D space.
Physics
In physics, the scalar projection is often used to calculate work done by a force. Work is defined as the dot product of the force and displacement vectors, which is essentially the scalar projection of the force onto the displacement vector times the magnitude of displacement.
For example, if a force is applied at an angle to the direction of motion, only the component of the force in the direction of motion works. The scalar projection allows us to isolate this component.
Computer Graphics and Game Development
In computer graphics, particularly in 3D gaming, vector projection plays a significant role in creating realistic motion and interactions.
For example, when you want a character to move along a surface, the motion in the direction perpendicular to the surface must be zero. This can be achieved by taking the desired motion vector, projecting it onto the surface normal (a vector perpendicular to the surface), and then subtracting that projection from the original vector. The result is a vector that lies entirely within the surface, creating a believable motion for the character.
Machine Learning
In machine learning, particularly in algorithms like Principal Component Analysis (PCA), projections are used extensively. PCA works by projecting multidimensional data onto fewer dimensions (the principal components) in a way that preserves as much of the data’s variation as possible.
These principal components are vectors, and the projected data points are scalar projections onto these vectors. This process can help to simplify datasets, reduce noise, and identify patterns that might be less clear in the full multidimensional space.
Geography
In the field of geography, vector projections are used to portray the 3D Earth on a 2D surface (like a map or a computer screen). This involves projecting geographical coordinates (which can be thought of as points on a sphere) onto a 2D plane.
There are many methods to do this (known as map projections), each with different advantages and trade-offs. For example, the Mercator projection preserves angles (which is useful for navigation) but distorts sizes and shapes at large scales.
Engineering
In structural engineering, the stress on a beam often needs to be resolved into components parallel and perpendicular to the beam’s axis. This is effectively projecting the stress vector in the relevant directions. Similarly, in signal processing (which is particularly important in electrical engineering), a signal is often decomposed into orthogonal components using the Fourier transform. This involves projecting the signal onto a set of basis functions, each representing a different frequency.
Historical Significance
The concepts of scalar and vector projections, while they are now fundamental elements of vector calculus, are relatively modern developments in the field of mathematics. They are rooted in the invention and refinement of vector analysis during the 19th century.
It is essential to remember that the idea of a vector itself wasn’t formally introduced until the mid-19th century. British physicist and mathematician Sir William Rowan Hamilton introduced quaternions in 1843, marking one of the first instances of a mathematical structure behaving like vectors as we understand them today.
Following Hamilton’s work, multiple mathematicians developed the notion of vectors. Josiah Willard Gibbs and Oliver Heaviside, working independently in the late 19th century, each developed systems of vector analysis to simplify the notation and manipulation of vector quantities in three dimensions. This work was mainly motivated by the desire to understand and encapsulate James Clerk Maxwell’s equations of electromagnetism more intuitively.
As part of these systems of vector analysis, the concepts of dot and cross products were introduced, and scalar and vector projections naturally arise from these operations. The dot product gives us a means to calculate the scalar projection of one vector onto another, and a simple multiplication by a unit vector provides the vector projection.
Despite their relatively recent historical development, these concepts have quickly become fundamental tools in a vast array of scientific and engineering disciplines, underlining their profound utility and power.
All images were created with MATLAB.
