Parallel Lines Cut by a Transversal – Definition and Examples

 This article aims to illuminate the fascinating patterns and properties that emerge from parallel lines cut by a transversal. From alternate interior angles to corresponding angles, the dance of lines and angles offers a mesmerizing insight into the symmetries and consistencies of the space that surrounds us.

Definition of Parallel Lines Cut by a Transversal

Parallel lines cut by a transversal means two parallel lines are intersected by a third line, and the intersecting line is called a transversal. In this geometric configuration, the transversal creates several angles with parallel lines. The resulting angles have specific relationships and names based on their positions relative to the parallel lines and the transversal.

Some of the angle pairs formed include corresponding angles, alternate interior angles, alternate exterior angles, and consecutive (or same-side) interior angles. These angle relationships are fundamental in geometry and serve as the basis for many geometric proofs and applications.

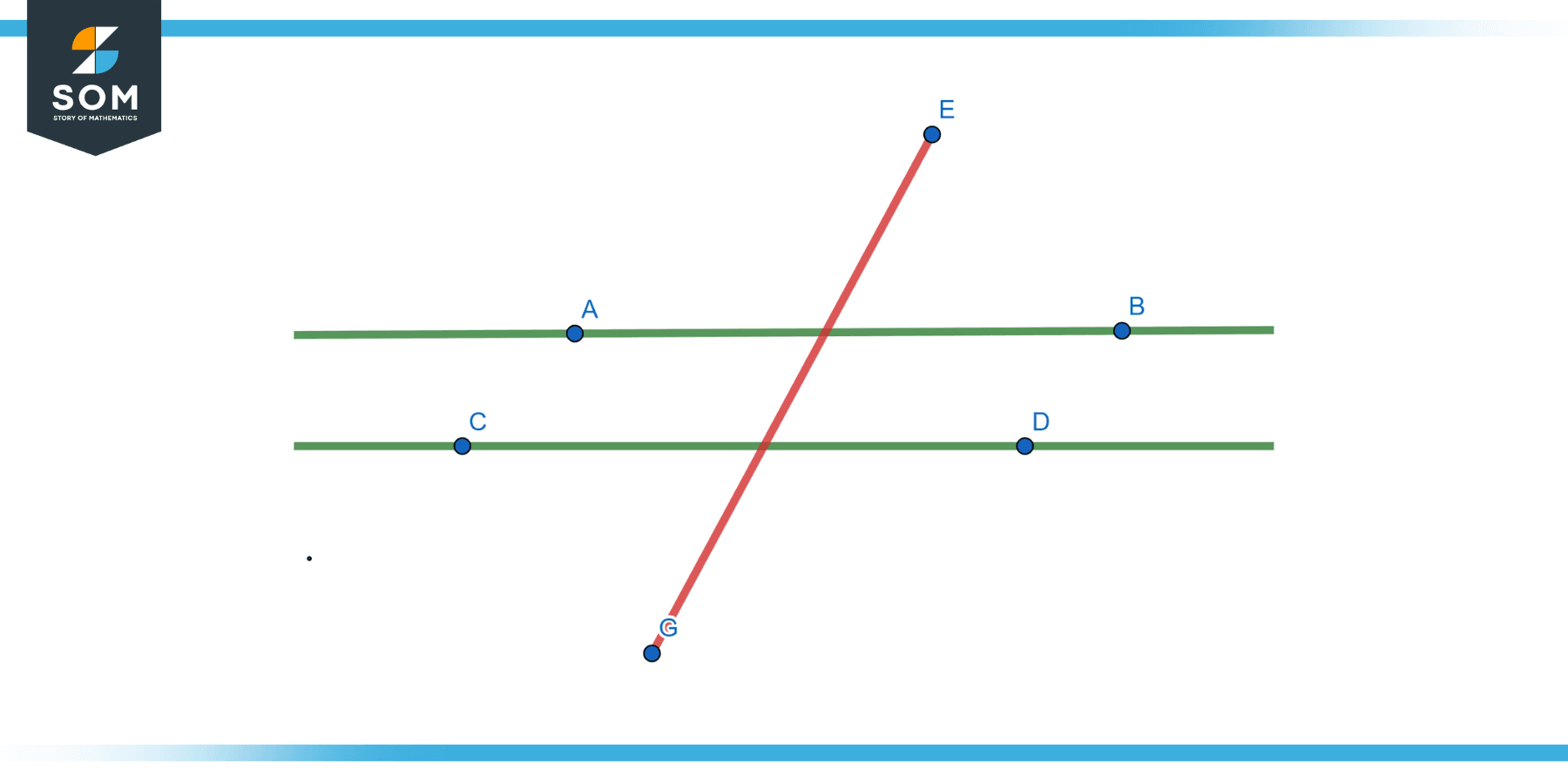
Figure-1.

Properties

When two parallel lines are intersected by a transversal, several important angle relationships and properties emerge. Let’s delve into these properties in detail:

• Corresponding Angles

  • Definition: Angles that are situated in the same position at each intersection where the transversal crosses the parallel lines.
  • Property: Corresponding angles are congruent (i.e., they have the same measure).
  • For example, if we label our parallel lines as l and m and the transversal as t, and the angle where t intersects l on the upper left is labeled as ∠1, then its corresponding angle where t intersects m would also be on the lower left.

• Alternate Interior Angles

  • Definition: Angles that are on opposite (alternate) sides of the transversal and lie between (interior to) the two parallel lines.
  • Property: Alternate interior angles are congruent.
  • Using our previous labeling, if ∠3 is an angle on the upper side of transversal t and inside lines l and m, its alternate interior angle would be on the lower side of t and also inside l and m.

• Alternate Exterior Angles

  • Definition: Angles that are on opposite sides of the transversal and lie outside (exterior to) the two parallel lines.
  • Property: Alternate exterior angles are congruent.

• Consecutive (Same-Side) Interior Angles

  • Definition: Angles that are on the same side of the transversal and lie between the two parallel lines.
  • Property: The sum of the measures of consecutive interior angles is 180∘180∘, meaning they are supplementary.

• Consecutive (Same-Side) Exterior Angles

  • Definition: Angles that are on the same side of the transversal and lie outside the two parallel lines.
  • Property: Like the interior version, consecutive exterior angles are supplementary.

• Vertical (or Opposite) Angles

  • Definition: When two lines intersect, the angles that are across from each other are called vertical or opposite angles.
  • Property: Vertical angles are congruent, but this is a more general property of intersecting lines and not specific to parallel lines cut by a transversal. However, since a transversal does intersect the parallel lines, vertical angles do form at each point of intersection.

These properties provide a solid foundation for many geometric proofs, especially those related to the properties of b. Understanding these relationships is also crucial in solving many geometric problems, as they often form the basis for determining unknown angle measures.

Exercise 

Example 1

Given two parallel lines and a transversal such that the measure of ∠1 = 40°. Find the measure of ∠5 (the corresponding angle to ∠1).

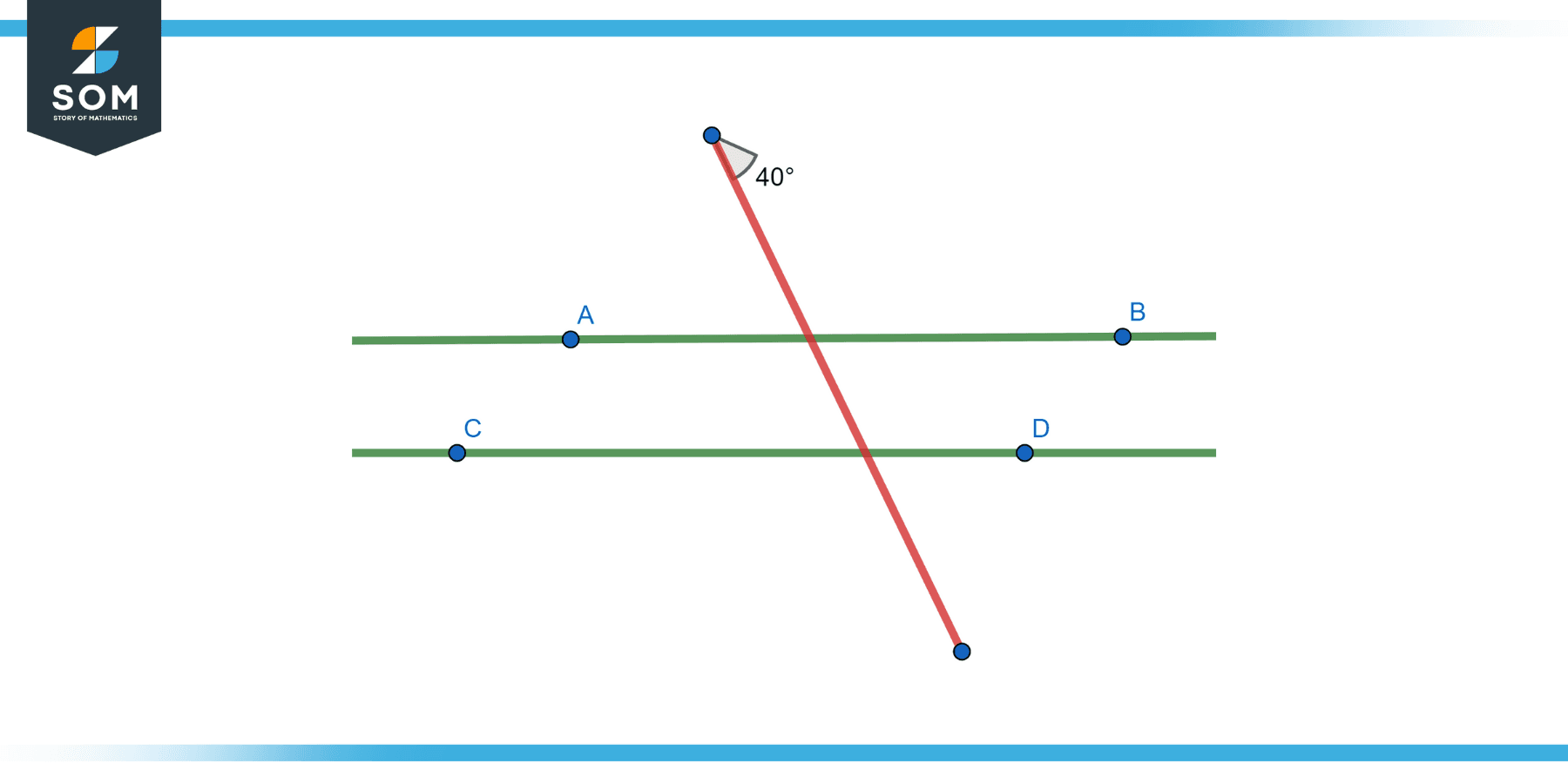
Figure-2.

Solution

Since ∠1 and ∠5 are corresponding angles, they are congruent.
Therefore, m∠5 = 40°.

Example 2

Given band a transversal with m∠3 = 110°, find m∠7 (the alternate interior angle to ∠3).

Solution

Alternate interior angles are congruent.
So, m∠7 = m∠3 = 110°.

Example 3

Given parallel lines cut by a transversal, if m∠4 = 70°, find m∠8 (the alternate exterior angle to ∠4).

Solution

Alternate exterior angles are congruent.
Therefore, m∠8 = m∠4 = 70°.

Example 4

If m∠2 = 120°, find the m∠6 (the consecutive interior angle to ∠2).

Solution

Consecutive interior angles are supplementary.
So, m∠2 + m∠6 = 180°.
Therefore, m∠6 = 180° – 120° = 60°.

Example 5

Given parallel lines and a transversal such that m∠3 = 85°, find m∠5 (the consecutive exterior angle to ∠3).

Solution

Since ∠3 and ∠5 are consecutive exterior angles, their measures add up to 180°.
Thus, m∠5 = 180° – 85° = 95°.

Example 6

Given that m∠1 = 50° and m∠3 = x, express x in terms of the given angles.

Solution

∠1 and ∠3 are vertical angles and therefore are congruent.
So, x = 50°.

Example 7

If m∠2 = y and m∠8 = 2y, determine the relationship between y and the angles.

Solution

∠2 and ∠8 are alternate interior angles, hence they are congruent.
Therefore, y = 2y, which is not possible unless y = 0°. But if y = 0°, then the lines would be perpendicular, not parallel. This means our original assumption that the lines are parallel is incorrect.

Example 8

Given parallel lines and a transversal such that m∠4 = z and m∠6 = 3z – 20. Find the value of z.

Solution

∠4 and ∠6 are consecutive interior angles, which are supplementary.
Thus, m∠4 + m∠6 = 180°.
z + (3z – 20) = 180
4z – 20 = 180
4z = 200
z = 50°

Applications 

Parallel lines cut by a transversal hold a significant position not just in the theoretical aspects of geometry, but also in various practical fields. The properties and relationships of angles formed by such configurations have practical implications and applications:

• Urban Planning and Architecture

  • City streets, especially in grid systems, often consist of parallel lines (streets) cut by transversals (avenues or cross streets). Understanding the properties of these angles helps in planning the layout, managing traffic flow, and optimizing space.
  • Architectural designs often use parallel lines and transversals in building layouts, determining angles of sunlight penetration, and planning structural supports.

• Transportation Engineering

  • Highways and roads are sometimes built parallel to each other for efficiency, and connecting roads or overpasses act as transversals. Understanding the angles and distances involved is crucial for safe and efficient road design.

• Railway Systems

  • Parallel tracks and the tracks that intersect them can be seen as a practical representation of parallel lines cut by a transversal. Safe distances, track-switching mechanisms, and intersection designs are influenced by these geometric principles.

• Art and Design:

  • Perspective drawing and linear perspective heavily rely on the concept of parallel lines and transversals. Parallel lines appear to converge at a vanishing point, a foundational concept in Renaissance art and most realist artistic techniques.

• Astronomy

  • Parallel lines and transversals can be used to explain phenomena like the transit of a planet across a star. The paths followed by celestial bodies and their relative alignments can sometimes be studied using these geometric principles.

• Navigation and Cartography

  • Latitude lines are parallel, and when ship or air routes (acting as transversals) cross these lines, understanding the angle relationships can be crucial for navigation.

• Computer Graphics and Gaming

  • Rendering realistic scenes, especially those with shadows, reflections, or linear patterns, often requires an understanding of how lines and angles relate to one another. The principles of parallel lines cut by a transversal can play a role in creating such graphics.

• Physics

  • In optics, when light rays (which can be parallel) are refracted or reflected by a surface or pass through a lens (acting as transversals), the angles they form can be crucial for predicting their behavior.

• Agriculture

  • Parallel farming rows with equipment or irrigation lines crossing them can be seen as a practical representation of this geometric concept. Understanding the angles and distances can optimize planting, irrigation, and harvesting.

In essence, while the concept of parallel lines cut by a transversal might seem purely theoretical, it has a broad spectrum of applications across diverse fields, contributing to the designs, efficiencies, and aesthetics of various aspects of our daily lives.

All images were created with GeoGebra.