Perimeter of a Square – Explanation & Examples - The Story of Mathematics - A History of Mathematical Thought from Ancient Times to the Modern Day

The perimeter of a square is the total length measured across its boundaries.

Let $x$ be the length of each side of the square, as shown in the figure below:

The perimeter is calculated using the formula:

$\textrm{Perimeter} = 4x$

The word perimeter is the combination of two Greek words, “Peri” meaning surrounding or enclosing of a surface, and “Meter” meaning measurement; so perimeter means total measurement of boundaries of a surface.

It is calculated by adding all the sides of a given geometrical figure, so if we add all the sides of a square, it will give us the perimeter of that square. This topic will help you understand the concept of the perimeter of a square and how to calculate it.

What Is the Perimeter of a Square?

The perimeter of a square is the total distance covered around its boundaries. A square is a closed polygon with four equal sides, so if we multiply 4 with any of the sides, it will give us the perimeter of the square.

Sometimes, we are given the diagonal or the area of a square, and we are asked to calculate the perimeter. We will discuss how to find a perimeter in these scenarios.

The units of the perimeter are the same as the units of the length of the sides of a square and are given in centimeters, meters, inches, feet, etc.

How To Find the Perimeter of a Square

To calculate the perimeter of a square, we have to add all the sides of the square. Consider the picture of a square given below.

If we add all the lengths, it will give us the perimeter of the square. This method is only applicable if we are given the length of any side of the square. In other cases, the perimeter can be calculated using:

The diagonal of the square
The area of the square

The given data will determine which method we have to use to calculate the perimeter of the square.

Perimeter of a Square Using the Length of Its Sides

This method is used when we are given the length of the sides of the square. To calculate the perimeter using this method we follow the steps below:

Write down the measurement of any one side of the square (for a square, all sides are equal).
Multiply the length of the given side by “4”.
Express the calculated perimeter in desired units.

Perimeter of a Square Using the Diagonal of the Square

This method is used when we are given the length of the diagonal of the square.

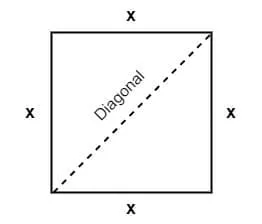
To calculate the perimeter using this method, we will follow the steps below:

Write down the measurement of the diagonal of the square.
Calculate the length of the sides of the square by dividing the diagonal by $\sqrt{2}$. $Side = \dfrac{diagonal} {\sqrt{2}}$.
The perimeter is calculated by multiplying the formula in step 2 by “4”. Perimeter $ = 4\times \dfrac{diagonal}{\sqrt{2}}$.

Perimeter $= (2\times 2) \dfrac{diagonal}{\sqrt{2}}$

Perimeter $= (2 \sqrt{2}) \times diagonal$

Perimeter of a Square Using the Area

This method is used when we are given the area of the square and no data regarding the length of the side of the square is given. To calculate the perimeter using this method, we will follow the steps listed below:

Write down the value of the area of the square.
Calculate the length of one side of the square by using the following formula: Side $= \sqrt{area}$.
The perimeter is calculated by multiplying the value of the side obtained in step 2 “4”. Perimeter $= 4\times \sqrt{area}$.

Perimeter of a Square Formula

The perimeter of a square is very easy to derive. As we discussed earlier, the perimeter is calculated by adding all the sides of the square.

Perimeter of square = side + side + side + side

Side = x

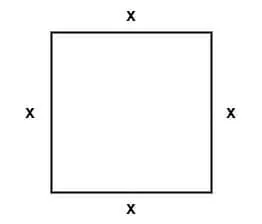
The perimeter of a square is $= x+x+x+x$

Perimeter of square $= 4\times x$

Real-life Applications of the Perimeter of a Square

The perimeter of a square can be used in numerous real-life applications. Various examples are given below:

We can use the perimeter of a square to determine or estimate the length of a garden having a square shape.
The perimeter formula is also helpful in designing a square table, cupboards and square swimming pool.
It is also helpful in construction plans of square offices or a square boundary around a house.
It is extremely helpful when farmers want to estimate the cost of fencing a square plot or a square farm.
This formula will come in handy when building a square barn for horses. The perimeter of the square will help you in the construction of the barn.

Example 1:

If the length of one side of the square is $7 \,cm$, what is the length of the remaining sides?

Solution:

We know that all the sides of a square are equal in length, so the length of the remaining three sides is also $7\,cm$ each.

Example 2:

Calculate the perimeter of a square for the figure given below.

Solution:

We are given the length of one side of a square and we know that all the sides of a square are equal in length.

Perimeter of the square $= 4\times side$

Perimeter of the square $= 4\times 6$

Perimeter of the square $= 24\,cm$

Example 3:

Suppose the perimeter of a square is $60\,cm$, what will be the length of all the sides of the square?

Solution:

We are given the perimeter of the square. We can calculate the length of a side of a square by using the perimeter formula

Perimeter of the square $= 4\times side$

$ 60 = 4\times side$

Side $= \dfrac{60}{4}$

Side $= 15 \,cm$

We know that all the sides of the square are equal in length, so all the sides of the square are $15 \,cm$ each.

Example 4:

If the length of one side of a square is $11 \,cm$, what will be the perimeter of the square?

Solution:

Perimeter of the square $= 4\times side$

Perimeter of the square $= 4\times 11$

Perimeter of the square $= 44\,cm$

Example 5:

A square garden has an area of $49\, meter^{2}$. What will be the perimeter of the garden?

Solution:

As the garden has a square shape, we can calculate the length of any side of the garden by using the formula.

Side $= \sqrt{area}$

Side $= \sqrt{49}$

Side $= 7 \,m$

Perimeter of the square garden $= 4\times side$

Perimeter of the square garden $= 4 \times 7$

Perimeter of the square garden $= 28\, m$

Example 6:

Nina is planning to design a square garden. If the length of the diagonal of the garden is $4\times \sqrt{2}\,meters$, what will be the perimeter of the garden?

Solution:

We are given the diagonal measurement of the garden.

Diagonal of the garden $= 4\times \sqrt{2}$ m

We can calculate the perimeter of the square garden by using the formula given below.

Perimeter of the garden $= (2\sqrt{2})\times \hspace{1mm} diagonal$

Perimeter of the garden $= (2\sqrt{2})\times 4 \sqrt{2}$

Perimeter of the garden $= 8\times 2$

Perimeter of the garden $= 16\,meters$

Practice Questions

1. If one side of the square is $10 \,cm$, what will be the length of the remaining sides and the value of the perimeter of the square?

2. If the perimeter of a square is $72\, cm$, what will be the length of the sides of the square?

3. Allan is designing a square table. Help Allan calculate the perimeter of the table using the data given below.

The length of one side of the table is $20\,cm$.
The diagonal of the table is $10\sqrt{2}\,cm$.
The area of the table is $36\, cm^{2}$.

4. Nina is planning on constructing a square barn for her horses. Help Nina calculate the perimeter of the barn in centimeters using the data given below.

The measurement of one side of the barn is $7\,meters$.
The diagonal measurement of the barn is $5\sqrt{2}\,meters$.
The area of the barn is $25\, meters^{2}$.

Answer Key

1. We are given the length of one side of the square and we know that all the sides of the square are equal so each side is = 10 cm.

Perimeter of the square $= 4\times side$

Perimeter of the square $= 4\times 10$

Perimeter of the square $= 40 \,cm$

2. We are given the perimeter of the square, so we have to find the length of one side of the square. Using the perimeter formula:

Perimeter of the square $= 4\times side$

$ 72 = 4\times side$

Side $= \dfrac{72}{4}$

Side $= \dfrac{60}{4}$

Side $= 18 \,cm$

As all the sides of the square are equal in length, the length of each side of the square is $= 18 \,cm$.

The length of one side of the square table is given, so we can calculate the perimeter by using the formula:

Perimeter of the table $= 4\times side$

Perimeter of the table $= 4\times 20$

Perimeter of the table $= 80\, cm$

The length of the diagonal of the table $= 10\sqrt{2}\, cm$

We can calculate the perimeter of the table by using the formula:

Perimeter $= (2\sqrt{2})\times\hspace{1mm} diagonal$

Perimeter of the square table $= (2\sqrt{2})\times 10 \sqrt{2}$

Perimeter of the table $= (10\times 2) ( \sqrt{2}\times \sqrt{2})$

Perimeter of the table $= (20) ( 2)$

Perimeter of the table $= 40\, cm$

Area of the table = $36\, cm^{2}$
We can calculate the length of one side of the table by using the formula:
Side $= \sqrt{area}$
Side $= \sqrt{36}$
Side $= 6\, cm$
Perimeter of the table $= 4\times side$
Perimeter of the table $= 4 \times 6$
Perimeter of the table $= 24 \,cm$

One side of the barn $= 7m$

Perimeter of the barn $= 4\times side$

Perimeter of the barn $= 4\times 7$

Perimeter of the barn $= 28 \,meters$

But we are asked to calculate the perimeter in centimeters, so we have to convert the answer into centimeters.

Perimeter of the barn $= 28 \times 100 = 2800$ cm

The length of the diagonal of the barn $= 5 \sqrt{2}\, meters$

Perimeter $= (2\sqrt{2})\times\hspace{1mm} diagonal$

Perimeter of the square table $= (2\sqrt{2})\times 5 \sqrt{2}$

Perimeter of the barn $= (5\times 2) ( \sqrt{2}\times \sqrt{2})$

Perimeter of the barn $= (10) ( 2)$

Perimeter of the barn $= 20\, m$

Perimeter of the barn $= 20 \times 100 = 2000\, cm$

Area of the barn = $25 \,m^{2}$

We can calculate the length of one side of the table by using the formula

Side $= \sqrt{area}$

Side $= \sqrt{25}$

Side $= 5 m$

Perimeter of the barn $= 4\times side$

Perimeter of the barn $= 4 \times 5$

Perimeter of the barn $= 20 \; meters$

Perimeter of the barn $= 20 \times 100 = 2000 \;cm$