JUMP TO TOPIC
The perimeter of a rhombus is the total length measured across its boundaries.
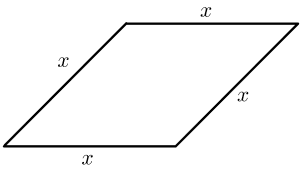
All sides of a rhombus are equal to each other. If the length of any single side is equal to $x$, as shown in the figure above, then the perimeter is given as
Perimeter $=4x$
We get the perimeter of a rhombus by adding the value of all of its sides. This topic will help you understand the properties of a rhombus and how to calculate its perimeter.
Before we jump to the topic, you must know the difference between a rhombus, a square, and a parallelogram, as all of them are quadrilaterals (i.e., four-sided geometrical figures) and share some commonalities. The differences between them is presented in the table below.
Parallelogram | Square | Rhombus |
| The opposite sides of a parallelogram are equal | All sides of a square are equal | All sides of a rhombus are equal |
| The opposite angles of a parallelogram are equal, while the adjacent angles supplement each other. | All angles ( interior & adjacent) are equal. All angles are right angles, i.e., 90 degrees. | The sum of two interior angles of a rhombus equals 180 degrees. Therefore, if all the angles of a rhombus are equal, they will be $90^o$ each, making it a square. |
| The diagonals of a parallelogram bisect each other. | The diagonals of the square are equal in length. | The diagonals of the rhombus bisect each other and are equal in length. |
| Every Parallelogram is not a rhombus. | Every rhombus is a parallelogram. | |
| All four sides of a square are perpendicular to each other. | The sides of a rhombus are not necessarily perpendicular. |
What Is the Perimeter of a Rhombus?
The perimeter of a rhombus is the total distance covered around its boundaries. A rhombus is a flat geometrical figure with four sides, and if we add the length of all four sides, it will give us the perimeter of the rhombus.
All sides of a rhombus are equal, similar to a square, and the perimeter is calculated by multiplying 4 with the length of a single side.
Take note that unlike a square, the four angles of a rhombus are not necessarily equal to $90^{o}$. A rhombus is a mixture of a rectangle and a square, and the properties of a rhombus are given below.
1. All four sides of a rhombus are equal to each other.
2. Opposite sides of a rhombus are parallel to each other.
3. The diagonals of a rhombus bisect each other at $90^{0}$.
4. The opposite angles of a rhombus are equal to each other.
5. Just like a rectangle, the sum of two adjacent angles of a rhombus is $180^{o}$.
The perimeter is a linear measure, so the units of the perimeter are the same as the units of the lengths of each side, i.e., centimeters, meters, inches, ft, etc.
How To Find the Perimeter of a Rhombus
The perimeter of a rhombus is defined as the sum of all the sides of a rhombus. If we add all sides, it will give us the perimeter of the rhombus. This method is only applicable if we are given the length of any one side of a rhombus.
Sometimes, we are given the diagonals of a rhombus and we are asked to find the perimeter. Thus, the given data determines which method we should use to calculate the perimeter of a rhombus.
Perimeter of a Rhombus Using the Side Method
This method is used when we are given the length of any one side of a rhombus. As discussed earlier, all the sides of a rhombus are equal. Therefore, if one side of a rhombus is “x,” then we can calculate the perimeter of the rhombus by multiplying “x” with 4.
Perimeter of a Rhombus Using the Diagonal Method
This method is used when we are given the length of the diagonals of a rhombus and no data regarding the lengths of the sides of the rhombus is available. However, we know that the diagonals of a rhombus bisect each other at a right angle, so when we draw the diagonals of a rhombus, it provides us with four congruent right-angled triangles, as shown in the picture below.
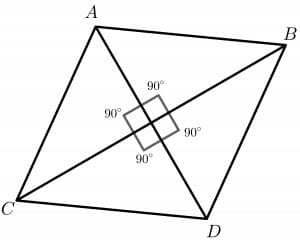
To calculate the perimeter by using this method, we follow the steps listed below:
- First, write down the measurements of the diagonals of the rhombus.
- Then, apply the Pythagorean theorem to get the value of any one side of the rhombus.
- Finally, multiply the calculated value in step 2 by “4”.
Perimeter of a Rhombus Formula
We can derive the formula for the perimeter of a rhombus by multiplying the length of any of the sides by “4”. We know that all the sides of a rhombus are equal, and we can write the formula for the perimeter of a rhombus as:
Perimeter of a rhombus $= x + x + x + x$
Perimeter of a rhombus $= 4\times x$
Perimeter of a Rhombus When Two Diagonals Are Given
Let us derive the formula of the perimeter of a rhombus when we are provided with the length of the diagonals. Consider this picture of a rhombus with the values of both diagonals available.
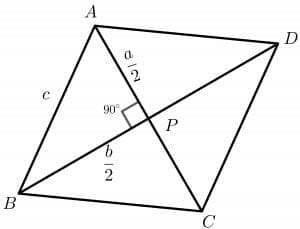
We can take any of the four triangles to solve for the formula. Lets us take the triangle ABP. We know the diagonals of the rhombus bisect each other at $90^{o}$, so we can write AP and BP as $\dfrac{a}{2}$ and $\dfrac{b}{2}$ respectively. Now, if we apply the Pythagorean theorem on the triangle ABP:
$ c^{2} = (\dfrac{a}{2})^{2} + (\dfrac{b}{2})^{2}$
$ c^{2} = (\dfrac{a^{2}}{4}) + (\dfrac{b^{2}}{4})$
$ c = \dfrac{\sqrt{(a^{2}+ b^{2})}}{2}$
We know that we can write the formula for the perimeter of the rhombus when one side (in this instance, the side “c”) is given as:
Perimeter of a rhombus $= 4 \times c$
Plugging the value of “c” in the above formula:
Perimeter of a rhombus $= 4 \times \dfrac{\sqrt{(a^{2}+ b^{2})}}{2}$
Perimeter of a rhombus $= 2 \times \sqrt{(a^{2}+ b^{2})}$
Note: You can also use the above formula to calculate the perimeter of the rhombus if you are provided with the length of one diagonal along with the area of the rhombus. Formula for the area of the rhombus $= \dfrac{diagonal\hspace{1mm} 1\times diagonal \hspace{1mm} 2}{2}$. So, we can calculate the length of the second diagonal using the area formula and then use the perimeter formula given above to calculate the perimeter of the rhombus.
Real-life Applications of the Perimeter of a Rhombus
The word perimeter is a combination of two Greek words: “Peri,” which means surrounding or boundaries of a surface or an object, and “Meter,” which means measurement of the surface or object, so perimeter means the total measurement of boundaries of a given surface.
With this information, we can use the perimeter of a rhombus in numerous real-life applications. Various examples are given below:
- For example, we can use the perimeter of a rhombus to calculate the distance of a pitcher’s spot from the striker in baseball if the whole pitch is shaped like a rhombus.
- The perimeter formula is also helpful in designing tables and cupboards having a rhombus shape.
- It is also helpful in the construction of rhombus-shaped offices and rooms.
Example 1:
If the length of one side of a rhombus is 11 cm, what will be the length of the rest of the sides?
Solution:
We know that all the sides of a rhombus are equal in length, so the length of the rest of the three sides is also 11 cm each.
Example 2:
Calculate the perimeter of a rhombus for the figure given below.
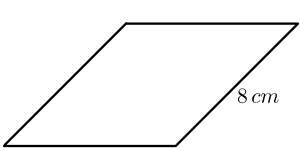
Solution:
We are given the length of one side of a rhombus, and we know that all the sides are equal in length.
Perimeter of the rhombus $= 4\times 8$
Perimeter of the rhombus $= 32 cm$
Example 3:
If the perimeter of a rhombus is 80cm, what will be the length of all the sides of the rhombus?
Solution:
We are given the perimeter of the rhombus. We can calculate the length of each side of a rhombus by using the perimeter formula:
Perimeter of a rhombus $= 4\times side$
$ 80 = 4\times side$
Side $= \frac{80}{4}$
Side $= \frac{80}{4}$
Side $= 20 cm$
All sides of the rhombus are 20 cm.
Example 4:
If the length of the diagonals of a rhombus is 9 cm and 11cm, what will be the perimeter of the rhombus?
Solution:
We are given the length of the two diagonals of the rhombus: let “a” and “b” be the two diagonals of the rhombus. Then, we can calculate the perimeter of the rhombus by using the formula given below.
Perimeter of the rhombus $= 2 \times \sqrt{(a^{2}+ b^{2})}$
Perimeter of the rhombus $= 2 \times \sqrt{(9^{2}+ 11^{2})}$
Perimeter of the rhombus $= 2 \times \sqrt{99 + 121}$
Perimeter of the rhombus $= 2 \times \sqrt{220}$
Perimeter of the rhombus $= 2 \times 14.83$
Perimeter of the rhombus $= 29.67 cm $ approx.
Example 5:
A rhombus has an area of $ 64 cm^{2}$, and the length of one diagonal of the rhombus is $8 cm$. What will be the perimeter of the rhombus?
Solution:
Let diagonal “a” = 8cm and we have to find “b”
Area of the rhombus $ = \dfrac{a\times b}{2}$
$64 = \dfrac{8\times b}{2}$
$128 = 8 \times b$
$ b = \dfrac{128}{8}$
$ b = 16 cm $
Perimeter of a rhombus $= 2 \times \sqrt{(a^{2}+ b^{2})}$
Perimeter of a rhombus $= 2 \times \sqrt{(8^{2}+ 16^{2})}$
Perimeter of a rhombus $= 2 \times \sqrt{64 + 256}$
Perimeter of a rhombus $= 2 \times \sqrt{320}$
Perimeter of a rhombus $= 2 \times 17.89$
Perimeter of a rhombus $= 35.78 cm $ approx.
Practice Questions
- If one side of a rhombus is $20 cm$, what is the length of the remaining sides and the perimeter of the rhombus?
- If the perimeter of a rhombus is $100 cm$, what is the length of the sides of the rhombus?
- If the length of the diagonals of a rhombus is $9 cm$ and $12cm$, what will be the rhombus’ perimeter and area?
- Consider a rhombus having an area of $36 cm ^{2}$ while the length of one of the diagonal is $4 cm$. What will be the perimeter of the rhombus?
Answer Key
1. We know that all sides of a rhombus are equal in length. If the length of one side of the rhombus is 20 cm, then the length of the remaining three sides will also be the same, i.e., 20 cm.
Perimeter of the rhombus $= 4\times side$
Perimeter of the rhombus $= 4\times 20$
Perimeter of the rhombus $= 80 cm$
2. We are given the perimeter of the rhombus. We can calculate the length of each side of the rhombus by using the perimeter formula:
Perimeter of a rhombus $= 4\times side$
$ 100 = 4\times side$
Side $= \frac{100}{4}$
Side $= 25 cm$
We know that all sides of a rhombus are equal in length, so all sides of the rhombus are $25 cm$ long.
3. We are given the lengths of the two diagonals of the rhombus. Let “a” and “b” be the two diagonals. Then, we can calculate the perimeter and area of the rhombus by using the values of the diagonals.
Area of the rhombus $ = \dfrac{a\times b}{2}$
Area of the rhombus $ = \dfrac{9\times 12}{2}$
Area of the rhombus $ = 9\times 6 = 54 cm^{2}$
Now let us calculate the perimeter of the rhombus.
Perimeter of a rhombus $= 2 \times \sqrt{(a^{2}+ b^{2})}$
Perimeter of a rhombus $= 2 \times \sqrt{(9^{2}+ 12^{2})}$
Perimeter of a rhombus $= 2 \times \sqrt{81 + 144}$
Perimeter of a rhombus $= 2 \times \sqrt{225}$
Perimeter of a rhombus $= 2 \times 15$
Perimeter of a rhombus $= 30 cm $ approx.
4. Let diagonal “a” $= 4 cm$ and we have to find “b”
Area of the rhombus $ = \dfrac{a\times b}{2}$
$36 = \dfrac{4 \times b}{2}$
$72 = 4 \times b$
$ b = \dfrac{72}{4}$
$ b = 18 cm $
Perimeter of a rhombus $= 2 \times \sqrt{(a^{2}+ b^{2})}$
Perimeter of a rhombus $= 2 \times \sqrt{(4^{2}+ 18^{2})}$
Perimeter of a rhombus $= 2 \times \sqrt{16 + 324}$
Perimeter of a rhombus $= 2 \times \sqrt{340}$
Perimeter of a rhombus $= 2 \times 18.44$
Perimeter of a rhombus $= 36.88 cm $ approx.
Images/Mathematical drawings are created using GeoGebra.
