Perimeter of a Parallelogram – Explanation & Examples

The perimeter of a parallelogram is the total length of its outer boundaries.

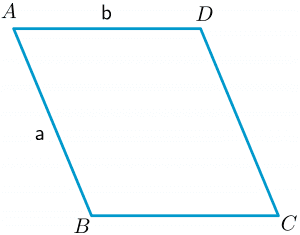
A parallelogram, similar to a rectangle, is a quadrilateral with equal opposite sides. So if the length and width of a parallelogram are $a$ and $b$, such as in the figure above, we can calculate the perimeter as:

Perimeter = $2(a + b)$

This topic will help you understand the concept of the perimeter of the parallelogram and how to calculate it. 

What Is the Perimeter of a Parallelogram?

The perimeter of a parallelogram is the total distance covered around its boundaries. A parallelogram is a quadrilateral, so it has four sides, and if we add up all the sides, it gives us the perimeter of the parallelogram. The formula for the perimeter of a parallelogram and rectangle is quite similar as both shapes share many properties.

Likewise, the formula for the area of a parallelogram and the area of a rectangle is also similar.

Let us discuss these topics in further detail. 

How To Find the Perimeter of a Parallelogram

The perimeter of a parallelogram is the sum of all four sides of the parallelogram. It is not necessary that we are given the values of all the sides of a parallelogram in all problems. In some cases, we might be given the base, height, and angle, and we will have to calculate the perimeter of the parallelogram from those values.

For example, we can calculate the perimeter of the parallelogram if we are given the following information:

1. Values of two adjacent sides are given
2. The value of one side and the diagonals are given
3. The values of the base, height, and angle are given

Perimeter of a Parallelogram Formula

The formula for the perimeter of a parallelogram is similar to that of the perimeter of a rectangle when the values of adjacent sides are given. However, the formula will be different when we are given base, height, and angle values, and similarly, it will be different when given the diagonal values.

Let us look at these formulas one by one.

Perimeter of a Parallelogram When Two Adjacent Sides Are Given

The formula for the perimeter of a parallelogram is the same as that of the perimeter of the rectangle in this scenario. Just like rectangles, the opposite sides of a parallelogram are equal.

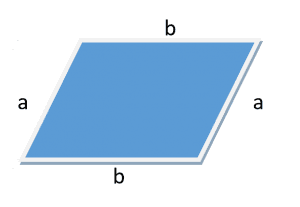
Perimeter of parallelogram $= a+b+a+b$

Perimeter of parallelogram $= 2 a + 2 b$

Perimeter of parallelogram $= 2 (a + b)$

Perimeter of a Parallelogram When the Base, Height and Angle Are Given

The formula for the perimeter of a parallelogram when the base, height, and angle are given is derived using the properties of a parallelogram. Consider the picture below.

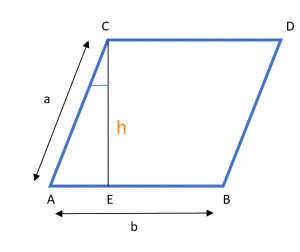
Here, “h” is the height and “b” is the base of the parallelogram while “Ɵ” is the angle between the height CE and side CA of the parallelogram. If we apply cosƟ to triangle ACE, we get,

 $cosƟ = \frac{h}{a}$

$a = \frac{h} {cosƟ}$

Therefore, the formula of the perimeter of a parallelogram when the base, height, and angle are known can be written as:

Perimeter of parallelogram $= 2 (\frac{h}{cosƟ} + b)$

Perimeter of a Parallelogram When One Side and Diagonals Are Given

The formula for the perimeter of a parallelogram when one side and diagonals are given is derived using the cosine theorem. For example, consider the parallelogram given below.

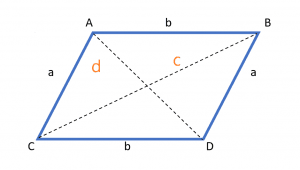
The sides of the parallelogram are ‘a’ and ‘b’, and diagonals are ‘c’ and ‘d’. Consider we are given the value of one side ‘a’, and the diagonals’ c’ and ‘d’, but the value of side ‘b’ is not known. Using this information, we can derive the perimeter formula using the law of cosines with the given data.

We start by applying the cosine theorem to triangle CDA:

$c^{2} = a^{2} + b^{2} – 2ab\hspace{1mm} cos ∠CDA$                        (1)

Now apply law of cosine to the triangle CAB:

$d^{2} = a^{2} + b^{2} – 2ab \hspace{1mm}cos ∠CAB$                        (2)

Add equation (1) and (2).

$c^{2} + d^{2} = 2a^{2} + 2b^{2} – 2ab (cos ∠CDA + cos ∠CAB)$                (3)

We know the adjacent angles of the parallelogram supplement each other, so:

$∠CDA + ∠CAB = 180^{o}$

$∠CDA = 180^{o} – ∠CAB$

Apply cosine on both sides:

$cos ∠CDA = cos (180^{o} – ∠CAB) = – cos ∠CAB$

$cos ∠CDA = – cos ∠CAB$               (4)

Substitute eq (4) in eq (3):

$c^{2} + d^{2} = 2a^{2} + 2b^{2} – 2ab ( – cos ∠CAB + cos ∠CAB)$

$c^{2} + d^{2} = 2a^{2} + 2b^{2} – 2ab (0)$

$c^{2} + d^{2} = 2a^{2} + 2b^{2}$

The above equation is the relation between the two sides and diagonals of the parallelogram. Now we have to find the relation for the unknown side “b”.

$2b^{2} = c^{2} + d^{2} – 2a^{2}$

$b^{2} = \frac{(c^{2} + d^{2} – 2a^{2})}{2}$

$b = \sqrt{ [\frac{(c^{2} + d^{2} – 2a^{2})}{2}]}$

Now we know the sides of the parallelogram (‘a’ and ‘b’) and hence we can use the formula from the previous section to find its perimeter (P).

Perimeter $= 2a + 2b$

Perimeter $= 2a + 2 \sqrt{ [\frac{(c^{2} + d^{2} – 2a^{2})}{2}]}$

Perimeter $= 2a + \sqrt{[2(c^{2} + d^{2} – 2a^{2})]}$

Perimeter $= 2a + \sqrt{(2c^{2} + 2d^{2} – 4a^{2})}$

Example 1: 

The length of adjacent sides of a parallelogram are $5 cm$ and $8 cm$, respectively. What will be the perimeter of the parallelogram?

Solution:

We are given the length of two adjacent sides of the parallelogram.

Let a $= 5cm$ and b $= 8cm$

We can now calculate the perimeter of the parallelogram with the formula we have studied earlier.

Perimeter of parallelogram $= 2 (a+ b)$

Perimeter of parallelogram $= 2 ( 5 cm+ 8 cm)$

Perimeter of parallelogram $= 2 ( 13 cm)$

Perimeter of parallelogram $= 26 cm$

Example 2: 

Calculate the perimeter of the parallelogram for the figure given below.

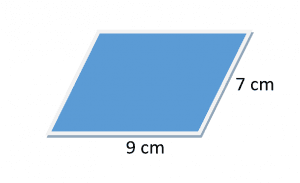
Solution:

We are given the length of two adjacent sides of the parallelogram.

Let a $= 9cm$ and b $= 7cm$  

We can now calculate the perimeter of a parallelogram with the formula we have studied earlier.

Perimeter of parallelogram $= 2 (a+ b)$

Perimeter of parallelogram $= 2 ( 9 cm+ 7 cm)$

Perimeter of parallelogram $= 2 ( 16 cm)$

Perimeter of parallelogram $= 32 cm$

Important Parallelogram Details

For us to fully understand this concept, let us learn some properties of a parallelogram and the differences between a parallelogram, a rectangle and a rhombus.

Knowing the differences among these two-dimensional, geometrical shapes will help you quickly understand and learn the topic without getting confused. Important properties of a parallelogram can be stated as:

1. Opposite sides of a parallelogram are congruent or equal.
2. Opposite angles of a parallelogram are equal to each other.
3. The diagonals of a parallelogram bisect each other.
4. The adjacent angles of a parallelogram supplement each other.

Now let us study the basic differences between the properties of a parallelogram, a rectangle, and a rhombus. The differences between these geometrical shapes are given in the table below.

Relation Between Area and Perimeter of a Parallelogram

The area of the parallelogram is the product of its base and height and it can be written as:

Area of parallelogram $= base \times height$.

We know the formula for the perimeter of the parallelogram is given as
Perimeter $= 2(a+b)$.

Here, “b” is the base, and “a” is the height.

Let us solve the equation for the value of “b”

$\frac{P}{2}= a + b$

$b = [\frac{p}{2}] – a$

Applying the value of “b” in the area formula:

Area $= [\frac{p}{2} – a] \times h.$

Example 3: 

If the area of a parallelogram is $42  \textrm{cm}^{2}$, and the base of the parallelogram is $6 cm$, what is the perimeter of the parallelogram?

Solution:

Let us take base and height of parallelogram as “b” and “h” respectively.

We are given the value of the base b = 6cm$

Area of a parallelogram is given as:

$A=b\times h$

$42 = 6 \times h$

Where as $b = 6\times a$

If we put the above value in the area formula, we get:

$h = \frac{42}{6}$

$h = 8cm$

Perimeter of parallelogram $= 2 (a + b)$

Perimeter of rectangle $= 2 (8 + 6)$

Perimeter of rectangle $= 2 ( 14 cm)$

Perimeter of rectangle $= 28 cm$

Practice Questions

1. Calculate the perimeter of the parallelogram using the data given below.

• Values of two adjacent sides are $8 cm$ and $11 cm$, respectively.
• Values of the base, height, and angle are $7 cm$, $5 cm$, and $60^{o}$, respectively.
• Values of diagonals are $5cm$ and $6cm$, while the value of one side is $7cm$.

2. Calculate the perimeter of a parallelogram when the length of one of its sides is 10 cm, its height is 20 cm, and one of the angles is 30 degrees.

Answer Key

1.

• We know the formula of perimeter of parallelogram:

Perimeter of parallelogram $= 2 ( a + b)$

Perimeter of parallelogram $= 2 ( 8 cm+ 11 cm)$

Perimeter of parallelogram  $= 2 ( 19 cm)$

Perimeter of parallelogram $= 38 cm$

• We know the formula of the perimeter of a parallelogram when the base, height, and angle is given:

Perimeter of parallelogram $= 2 (\frac{h}{cosƟ} + b)$

Perimeter of parallelogram $= 2 (\frac{5}{cos45^{o}} + 7)$

Perimeter of parallelogram $= 2 (\frac{5}{0.2} + 7)$

Perimeter of parallelogram $= 2 (10 + 7)$

Perimeter of parallelogram $= 2 (17)$

Perimeter of parallelogram $= 34 cm$

• We know the formula of the perimeter of a parallelogram when both diagonals and one side is given:

Perimeter $= 2a + \sqrt{(2c^{2} + 2d^{2} – 4a^{2})}$

Where, c $= 5 cm$, d $= 7cm$ and a $= 4 cm$

Perimeter $= 2\times 8 + \sqrt{(2\times5^{2} + 2\times 7^{2} – 4\times4^{2})}$

Perimeter $= 16 + \sqrt{(2\times 25 + 2\times 49 – 4\times 16)}$

Perimeter $= 16 + \sqrt{(50 + 98 – 64)}$

Perimeter $= 16 + \sqrt{(84)}$

Perimeter $= 16 + 9.165 $

Perimeter $= 25.165 cm$ approx.

2. We know the formula of the perimeter of a parallelogram when the base, height, and angle is given:

Perimeter of parallelogram $= 2 (\frac{h}{cosƟ} + b)$

Perimeter of parallelogram $= 2 (\frac{20}{cos30^{o}} + 10)$

Perimeter of parallelogram $= 2 (\frac{5}{0.866} + 10)$

Perimeter of parallelogram $= 2 (5.77 + 10)$

Perimeter of parallelogram $= 2 (15.77)$

Perimeter of parallelogram $= 26.77 cm$ approx.