JUMP TO TOPIC
Perimeter of a rectangle is the total length of all of its sides.
It is calculated with the help of the following formula:
$\textrm{Perimeter of a Rectangle} = 2 ( \textrm{Length} + \textrm{Width})$.
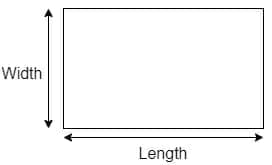
Perimeter is defined as the boundary that surrounds a shape. It can also be defined as the length of a shape’s sides. A rectangle is a quadrilateral (i.e., a figure with four sides) whose opposite sides are equal; therefore, we only need to know its length and width to find the perimeter.
What Is the Perimeter of a Rectangle?
The perimeter of a rectangle is the total distance around its boundaries. In other words, a rectangle has four sides, and if we add up all the sides, it will give us the perimeter of the rectangle. As the opposite sides of a rectangle are equal, two times width plus two times length will also give us the same result.
How To Find the Perimeter of a Rectangle
Consider the picture of a rectangle given below.
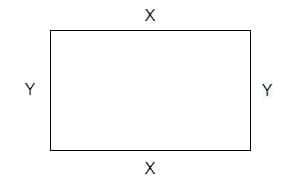
Here, $X$ is the length of a rectangle, and $Y$ is the width or breadth of the rectangle.
The perimeter of a rectangle will be $ X+X+Y+Y$. As we are adding up the sides, the unit of the parameter will be the same as the unit of each of the sides, i.e., meters, centimeters, inches, etc.
Formula for Perimeter of a Rectangle
The formula for the perimeter of a rectangle is easy to derive. We know that the opposite sides of the rectangle are equal to each other, so we can write the equation for the calculation of the perimeter of the rectangle as:
Perimeter of a rectangle = Length + Width + Length + Width
If length = $X$ and width = $Y$
Then the perimeter of a rectangle is $ X\hspace{1mm}+\hspace{1mm}Y\hspace{1mm}+\hspace{1mm}X\hspace{1mm}+\hspace{1mm}Y$
Perimeter of a rectangle $= 2 X\hspace{1mm} + \hspace{1mm}2 Y$
Perimeter of a rectangle $= 2 (X\hspace{1mm} +\hspace{1mm} Y)$
Let us look at an example:
Calculate the perimeter of the rectangle for the figure given below.
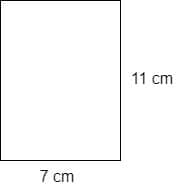
So we are provided with the values of one length and one width of the rectangle. We know that the opposite sides of the rectangle are congruent, so we can write Length $(X) = 7 $cm and Width $(Y) = 11$ cm. The perimeter of the given rectangle can be calculated as:
Perimeter of rectangle $= 2 (X \hspace{1mm}+\hspace{1mm} Y)$
Perimeter of rectangle $= 2 (7cm \hspace{1mm}+\hspace{1mm} 11cm)$
Perimeter of rectangle $= 2 (18 cm)$
Perimeter of rectangle $= 36 \hspace{1mm}cm$
Real-life Applications of Perimeter of a Rectangle
The perimeter of a rectangle is used in numerous real-life applications.
Various examples are given below:
- We can use the perimeter of a rectangle to determine or estimate the length of a rectangular area such as a garden or a whiteboard.
- The perimeter formula is also helpful in designing a rectangular swimming pool or a rectangular-shaped cupboard.
- It is also helpful in the construction plans of offices and houses where we need to set a rectangular boundary.
Example 1
Calculate the perimeter of the rectangle in the figure given below.
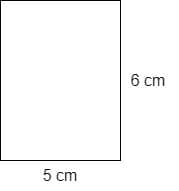
Solution
The above figure shows that the length of one side of the rectangle is $5$ cm and the width is $6$ cm.
We know that the opposite sides of a rectangle are equal, so the complete figure is shown below:
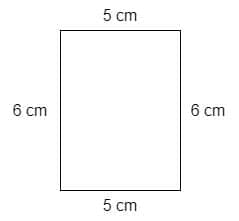
We can now calculate the perimeter of the rectangle using either the definition of perimeter as the sum of the lengths of all sides or with the formula we have studied earlier:
Perimeter of rectangle $= L \hspace{1mm}+W \hspace{1mm}+\hspace{1mm}L+\hspace{1mm}W$
Perimeter of rectangle $= 5 cm\hspace{1mm} +\hspace{1mm}6 cm \hspace{1mm}+\hspace{1mm}5 cm+\hspace{1mm}6 cm$
Perimeter of rectangle $= 22 cm$
Alternative solution
Perimeter of rectangle $= 2 ( W\hspace{1mm}+\hspace{1mm} L)$
Perimeter of rectangle $= 2 ( 6 cm\hspace{1mm}+\hspace{1mm} 5 cm)$
Perimeter of rectangle $= 2 ( 11 cm)$
Perimeter of rectangle $= 22 \hspace{1mm}cm$
Example 2
The length of a rectangle is $16$cm and its width is $10$ cm. What will be the perimeter of the rectangle?
Solution
We are given the length and the width of the rectangle and we know that the opposite sides of the rectangle are equal, so the perimeter of the rectangle can be calculated as:
Perimeter of rectangle $= L\hspace{1mm} + \hspace{1mm}W +\hspace{1mm} L \hspace{1mm}+\hspace{1mm} W$
Perimeter of rectangle $= 16cm \hspace{1mm}+\hspace{1mm} 10cm\hspace{1mm} +\hspace{1mm} 16cm +\hspace{1mm} 10cm$
Perimeter of rectangle $= 52 \hspace{1mm}cm$
Alternative solution
Perimeter of rectangle $= 2 ( W\hspace{1mm}+\hspace{1mm} L)$
Perimeter of rectangle $= 2 ( 16\hspace{1mm} cm+ \hspace{1mm}10 cm)$
Perimeter of rectangle $= 2 ( 26 cm)$
Perimeter of rectangle $= 52 \hspace{1mm}cm$
Calculation of the Perimeter When the Area Is Given
In some cases, you might know the area of a rectangle and you are asked to find the perimeter. For such questions, the solution requires understanding and solving the quadratic equation. If you want to learn how to solve a quadratic equation, click here.
Let us recall the formula for the area of the rectangle first:
Area of rectangle $= ( Length \times Width) = X \times Y$.
Let us discuss some examples where an area of a rectangle is given and we are required to calculate the perimeter of the rectangle.
Example 3
If the area of a rectangle is 24 square inches and the width of the rectangle is 6 times its length, what is the perimeter of the rectangle?
Solution:
Let us consider the rectangle’s length and width as “a” and “b,” respectively.
As width is $6$ times greater than length, so $b = 6 a$
The area of a rectangle is given as:
$A=L\times W$
$A = a \times b$,
where $b = 6\times a$
If we put the value of $b$ in the formula for the area, we get:
$A = a \times 6a$
$24 = 6a^{2}$
$4=a^{2}$
$a = L = 2$
So, $y = W = 6a = 6\times2 = 12$
Length $= 2$ inches and width $= 12 $ inches
Perimeter of rectangle $= 2 ( W\hspace{1mm}+\hspace{1mm} L)$
Perimeter of rectangle $= 2 ( 12\hspace{1mm} +\hspace{1mm} 2)$
Perimeter of rectangle $= 2 ( 14 )$.
Perimeter of rectangle $= 28\hspace{1mm} inches$.
Example 4
A rectangular garden has an area of 32 square meters. The length is four units smaller than the width. What is the perimeter of the garden?
Solution:
We know the formula for the area of a rectangle is:
Area $= L \times W$
The length is four units smaller than the width, $L = W\hspace{1mm}-\hspace{1mm} 4 $
Let $L = a$ and $W = b$
$a = b \hspace{1mm}-\hspace{1mm} 4 $
So, if we put this value in the area formula, we get:
Area $= (b \hspace{1mm}–\hspace{1mm} 4) b$
$32 = b^{2} \hspace{1mm}–\hspace{1mm} 4b$
$b^{2}\hspace{1mm} –\hspace{1mm} 4b\hspace{1mm} –\hspace{1mm} 32 = 0$
Solving the quadratic equation:
$b^{2}\hspace{1mm} –\hspace{1mm} 8b \hspace{1mm}+\hspace{1mm}4b \hspace{1mm}–\hspace{1mm} 32 = 0$
$b (b – 8) +4 (b – 8) = 0$
$(b \hspace{1mm}–\hspace{1mm} 8) (b\hspace{1mm}+\hspace{1mm} 4) = 0$
So, $b = 8$ and $b = – 4$
The width cannot be negative, so the width of the garden is 8 meters.
Now we can easily calculate the value of the length.
$a = b\hspace{1mm} –\hspace{1mm} 4 = 8\hspace{1mm} –\hspace{1mm} 4 = 4$
Length $= 4 $ meters and width $= 8 $ meters
Perimeter of garden $= 2 ( W\hspace{1mm}+\hspace{1mm} L)$
Perimeter of garden $= 2 ( 8 m\hspace{1mm}+\hspace{1mm} 4 m)$
Perimeter of garden $= 2 ( 12 m)$
Perimeter of garden $= 24\hspace{1mm} meters$
Example 5
Archer plans to design a rectangular whiteboard for his class. He wants the total area of the board to be $100$ square centimeters. If the length of the board is going to be $10$ centimeters less than twice the width, what will the perimeter of the whiteboard be in centimeters?
Solution:
Let us consider the length of the board as “a” and the width as “b.”
As the length of the board is ten centimeters less than twice the width, the equation can be written as: $a = 2b\hspace{1mm} –\hspace{1mm} 10$.
Area of the rectangle is $= 100 cm^{2}$
Formula for the area of a rectangle is given as:
$A = L \times W$
$A = a \times b$
Let us plug in the value of length in the above equation
$A = (2b \hspace{1mm}–\hspace{1mm} 10) \times b$
$100 = 2b^{2}\hspace{1mm} –\hspace{1mm} 10b$
$50 = b^{2} \hspace{1mm}–\hspace{1mm} 5b$
Solve for the width:
$b^{2}\hspace{1mm}-\hspace{1mm} 5b\hspace{1mm} -\hspace{1mm} 50 = 0$
$b^{2} \hspace{1mm}–\hspace{1mm} 10b \hspace{1mm}+ \hspace{1mm}5b \hspace{1mm}- \hspace{1mm}50 = 0$
$b (b \hspace{1mm}–\hspace{1mm} 10) + 5(b \hspace{1mm}–\hspace{1mm} 10) = 0$
$(b \hspace{1mm}–\hspace{1mm} 10 )(b\hspace{1mm} +\hspace{1mm} 5) = 0$
$b = 10 \hspace{1mm}and\hspace{1mm} b = – 5$
The width can either be $-5$ or $10$, and as width cannot be negative, the value of width is $10$.
If $b = 10 cm$, then the value of the length is $a = 2(10)\hspace{1mm} -\hspace{1mm} 10 = 10 cm$.
Now we know the values of the width and length of the rectangular board. With this information, we can calculate its perimeter by putting the values in the formula.
Perimeter of the rectangular board $= 2 L\hspace{1mm} +\hspace{1mm} 2 W = 2(10 cm) + 2(10 cm) = 40 \hspace{1mm}cm$.
Practice Questions:
- If the length and the width of a rectangle are $6 cm$ and $8 cm$ respectively, what will be the perimeter of the rectangle?
- If the length and the width of a rectangle are $10 cm$ and $7 cm$ respectively, what will be the perimeter of the rectangle?
- Ahmad is designing a rectangular garden. Help Ahmad calculate the perimeter of the garden from the data given below. Length of garden $= 8 cm$ and width $= 5 cm$. Length of garden $= 6 cm$ and width $= 9 cm$. The area of the garden is $16$ square meters and width $= 8 m$
- Nathan plans to design a rectangular swimming pool in his backyard. He wants the total area of the pool to be $64$ square meters. If the length of the board is going to be $4$ meters less than the width, what will the perimeter of the pool be in meters?
Answer Key:
1. We know the formula of the perimeter of rectangle:
Perimeter of rectangle $= L \hspace{1mm}+\hspace{1mm} W\hspace{1mm} +\hspace{1mm} L +\hspace{1mm} W$
Perimeter of rectangle $= 6cm\hspace{1mm} +\hspace{1mm} 8cm\hspace{1mm} +\hspace{1mm} 6cm \hspace{1mm}+\hspace{1mm} 8cm$
Perimeter of rectangle $= 28 \hspace{1mm}cm$
Alternative solution
Perimeter of rectangle $= 2 ( L\hspace{1mm}+ \hspace{1mm}W)$
Perimeter of rectangle $= 2 ( 6\hspace{1mm} cm+\hspace{1mm} 8 cm)$
Perimeter of rectangle $= 2 ( 14 cm)$
Perimeter of rectangle $= 28 \hspace{1mm}cm$
2. We know the formula for perimeter of a rectangle:
Perimeter of rectangle $= L \hspace{1mm}+\hspace{1mm} W\hspace{1mm} +\hspace{1mm} L\hspace{1mm} +\hspace{1mm} W$
Perimeter of rectangle $= 10 cm \hspace{1mm}+\hspace{1mm} 7 cm \hspace{1mm}+\hspace{1mm} 10 cm\hspace{1mm} +\hspace{1mm} 7 cm$
Perimeter of rectangle $= 34 \hspace{1mm}cm$
Alternative solution
Perimeter of rectangle $= 2 ( L\hspace{1mm}+ \hspace{1mm}W)$
Perimeter of rectangle $= 2 ( 10 cm+ 7 cm)$
Perimeter of rectangle $= 2 ( 17 cm)$
Perimeter of rectangle $= 34\hspace{1mm} cm$
3.
- Length $= 8 cm$ and Width $= 5 cm$
We can calculate the perimeter of the rectangular garden by using the perimeter formula.
Perimeter of rectangle $= 2 ( L\hspace{1mm}+\hspace{1mm} W)$
Perimeter of rectangle $= 2 ( 8 cm\hspace{1mm}+\hspace{1mm} 5 cm)$
Perimeter of rectangle $= 2 ( 13 cm)$
Perimeter of rectangle $= 26 \hspace{1mm}cm$.
- Length $= 6 cm$ and Width $= 9 cm$
We can calculate the perimeter of the rectangular garden by using the perimeter formula.
Perimeter of rectangle $ = 2 ( L\hspace{1mm}+\hspace{1mm} W)$
Perimeter of rectangle $ = 2 ( 6 cm+ 9 cm)$
Perimeter of rectangle $ = 2 ( 15 cm)$
Perimeter of rectangle $ = 30\hspace{1mm} cm$
- Area of garden = $16 m ^{2} $ and Width = $8m$
$A = L\times W$
$16 = L\times 8$
$L = 2 \hspace{1mm}m$
Now that we have the length and the width of the garden, we can now calculate the perimeter by using the formula.
Perimeter of rectangle $ = 2 ( L\hspace{1mm}+\hspace{1mm} W)$
Perimeter of rectangle $ = 2 ( 2 cm+ 8 cm)$
Perimeter of rectangle $ = 2 ( 10 cm)$
Perimeter of rectangle $ = 20\hspace{1mm} cm$
4. Let us take length $= x$ and Width $= y$
As the length of the pool is four meters less than that of the width, the resultant equation can be written as: $x = y \hspace{1mm}-\hspace{1mm} 4$.
Area of the pool is $= 12\; meter ^ {2}$
Formula for area of rectangle is given as:
$A = L \times W$
$A = x \times y$
$A = (y \hspace{1mm}– \hspace{1mm}4) y$
$12 = y^{2} \hspace{1mm}–\hspace{1mm} 4y$
$y^{2}\hspace{1mm}- \hspace{1mm}4y \hspace{1mm}-\hspace{1mm} 12 = 0$
$y^{2} \hspace{1mm}-\hspace{1mm} 6y \hspace{1mm}+ \hspace{1mm}2y \hspace{1mm}- \hspace{1mm}12 = 0$
$y (y \hspace{1mm}–\hspace{1mm} 6) + 2(y\hspace{1mm} –\hspace{1mm} 6) = 0$
$(y \hspace{1mm}– \hspace{1mm}6 )(y\hspace{1mm} +\hspace{1mm} 5) = 0$
The width can either be $-5$ or $6$ and as width cannot be negative, the value of width is $6$.
So $y = W = 6$, then value of the length $L = W \hspace{1mm}-\hspace{1mm} 4 = 6\hspace{1mm} -\hspace{1mm} 4 = 2 \hspace{1mm} meters$
Now we know the values of the width and the length of the rectangular swimming pool. We can then calculate its perimeter by putting the values in the formula.
Perimeter of the swimming pool $= 2 (L \hspace{1mm}+\hspace{1mm} W) = 2(2m \hspace{1mm}+\hspace{1mm} 6m) = 2(8m) = 16\hspace{1mm} meters.$
