JUMP TO TOPIC
Inverse function theorem gives a sufficient condition for the existence of the inverse of a function around a certain point and also tells us how to find the derivative of the inverse function at that point.
To understand the inverse function theorem, let us first recall what is a function and what is the inverse of a function. A function in mathematics is an expression that gives us a relationship between two variables, so consider a function denoted by “$f$” and let the inverse of this function be denoted by “$g$”.
If the function satisfies the equation $f(a) = b$, then the inverse of this function satisfies $g(b) = a$. The inverse of a function is denoted by $f^{-1}$.
What Is the Inverse Function Theorem?
The inverse function theorem states that if a function “$f$” is a continuously differentiable function, i.e., the variable of the function can be differentiated at each point in the domain of $f$, then the inverse of that function will also be a continuously differentiable function and the derivative of the inverse function will be the reciprocal of the derivative of the original function.
Let $f(x)$ be a one-to-one function and $f'(a)$ is not $0$, where $f’$ denotes the derivative of $f$, then by the inverse function theorem:
- $f^{-1}$ exists around $b=f(a)$ and is also differentiable around $b$.
- $\frac{d}{dx}f^{-1}(x)|_b = \frac{1}{f'(a)}$.
The inverse function theorem is only applicable to one-to-one functions. The inverse function theorem is used in solving complex inverse trigonometric and graphical functions. We will study different types of inverse functions in detail, but let us first clear the concept of a function and discuss some of its types to get a clearer picture.
Function
A function in mathematics is used to define the relationship between two variables. One variable is called the independent while the other variable is termed the dependent variable. For example, for function $f(x) = y$ the variable “$x$” is the independent variable while the variable “$y$” is the dependent variable.
In set-theoretic terms, a function is a mapping between two sets, say $A$ and $B$, where $x\in A$ and $y\in B$. Note that $A$ is called the domain of $f$ and $B$ is called the co-domain. The range of $f$ is a subset of $B$ consisting of all elements $b$, i.e., $f(a)=b$ for some $a$ in $A$.
Functions can be classified into many types such as one-to-one and many-to-one, etc.
One to One Function
In a one-to-one function, each element of the domain is connected to only one element of the codomain. Inverse function theorem deals with one-to-one functions only.
Many to One Function
In many to one functions, as the name suggests, multiple elements of the domain are mapped to a single element of the codomain. For such functions, inverse functions do not exist.
Inverse Function Calculation
The inverse of a function and its derivation depends upon the type of problem we are given. It is essential to first understand how the inverse of a function is calculated before we jump to the inverse function theorem.
Finding Inverse Through Swapping
We can find the inverse of a function with ordered pairs by simply swapping the values of “$x$” and “$y$”.
Consider a function $f(x) = {(1,2), (2,4), (5,7) ,(3,9)}$
We have already discussed that inverse is only applicable when we have one to one function and in this example, the values of “$x$” and “$y$” are used once and there is no repetition. So the inverse of the function can be calculated by simply swapping the values of “$x$” and “$y$”.
$f^{-1}(x) = {(2,1),(4,2),(7,5),(9,3)}$
Example 1:
Without using the inverse of a function, find out the domain and range of $f^{-1}(x)$.
- $f(x) = (x-6)^{2} , x\geq 6$
- $f(x) = \sqrt{x+4}$
- $f(x) = \sqrt{x-2}$
Solution:
1. $f(x) = (x-6)^{2}$
We know $x\geq 6$
So, $Domain \hspace{1mm} of \hspace{1mm} f(x) = [ 6, \infty) \hspace{1mm} and\hspace{1mm} range \hspace{1mm}of \hspace{1mm}f(x) = [ 0, \infty)$
So,
$Domain \hspace{1mm} of \hspace{1mm} f^{-1}(x) = range\hspace{1mm} of\hspace{1mm} f(x) = [ 0, \infty)$
$Range \hspace{1mm} of \hspace{1mm}f^{-1}(x)$ = $Domain \hspace{1mm} of \hspace{1mm} f^{-1}(x)$ = $[ 6, \infty)$
2. Let $y =f(x)$
“$y$” will be real if $x\geq -4$
$y = \sqrt{x+4}$
So, $Domain\hspace{1mm} of\hspace{1mm} f(x) = [ -4, \infty) \hspace{1mm} and\hspace{1mm} range\hspace{1mm} of\hspace{1mm} f(x) = [ 0, \infty)$
So,
$Domain \hspace{1mm} of \hspace{1mm}f^{-1}(x) = range\hspace{1mm} of\hspace{1mm} f(x) = [ 0, \infty)$
$Range\hspace{1mm} of \hspace{1mm} f^{-1}(x)$ = $Domain \hspace{1mm} of \hspace{1mm}f(x) = [ -4, \infty)$
3. Let $y =f(x)$
“$y$” will be real if $x\geq 4$
$y = \sqrt{x-4}$
So, $Domain\hspace{1mm} of\hspace{1mm} f(x) = [ 4, \infty) \hspace{1mm} and\hspace{1mm} range\hspace{1mm} of\hspace{1mm} f(x) = [ 0, \infty)$
So,
$Domain \hspace{1mm} of \hspace{1mm}f^{-1}(x) = range\hspace{1mm} of\hspace{1mm} f(x) = [ 0, \infty)$
$Range\hspace{1mm} of \hspace{1mm} f^{-1}(x)$ = $Domain \hspace{1mm} of \hspace{1mm}f(x) = [ 4, \infty)$
Finding Inverse Through Algebra
This method is quite similar to the swapping method but it requires some mathematical calculations. In this method, we simply swap the variables and then solve the equation. For example, consider a function $f(x) = 4x +3$ here $y= f(x)$.
$y = 4x +3$
Now swap both variables:
$x = 4y+3$
$y = \dfrac{x-3}{4}$
$f^{-1}(x) = \dfrac{x-3}{4}$
We can also demonstrate the inverse of an algebraic function through a graph. The equation $y=x$ gives us a straight line passing through the origin. The inverse function appears as the mirror image of the original image along the $y=x$ line. Consider a function $f(x)= 2x+5$, and the inverse of this function is $f^{-1}(x) = \dfrac{x-5}{2}$.
Now let’s take a look at the graphical representation below.
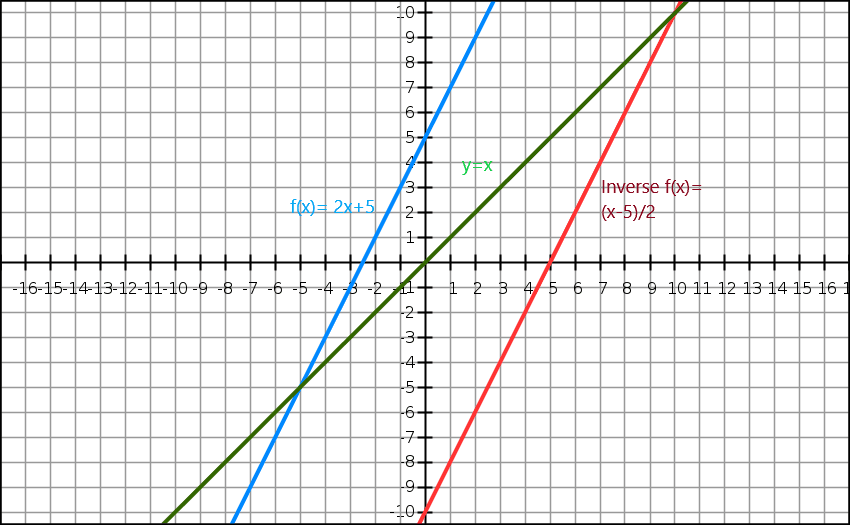
Here, the blue line is the original function while the green line shows y=x. We can clearly see that the red line which is the inverse function of f(x) is the mirror image of the original function and it is present on the opposite side of the line y = x.
Example 2:
Using the functions given below, find $f^{-1}(x)$ and $f^{-1}(2)$.
- $f(x) = -4x +6$
- $f(x) = 2x +8$
- $f(x) = -8x +4$
Solution:
1. Let $y=f(x)$
$y = -4x + 6$
Now swap both variables:
$x = -4y+6 $
$y = -\dfrac{x-6}{4}$
$f^{-1}(x) = -\dfrac{x-6}{4}$
$f^{-1}(2) = -\dfrac{2-6}{4}$
$f^{-1}(2) = -\dfrac{-4}{4}$
$f^{-1}(2) = 1$
2. Let $y=f(x)$
$y = 2x + 8$
Now swap both variables:
$x = 2y+8$
$y = \dfrac{x-8}{2}$
$f^{-1}(x) = \dfrac{x-8}{2}$
$f^{-1}(2) = \dfrac{2-8}{4}$
$f^{-1}(2) = \dfrac{-6}{4}$
$f^{-1}(2) = -\dfrac{3}{2}$
3. Let $y=f(x)$
$y = -8x + 4$
Now swap both variables:
$x = -8y+4$
$y = -\dfrac{x-4}{8}$
$f^{-1}(x) = -\dfrac{x-4}{8}$
$f^{-1}(2) = -\dfrac{2-4}{4}$
$f^{-1}(2) = -\dfrac{-2}{8}$
$f^{-1}(2) = \dfrac{1}{4}$
Inverse Function Theorem Proof
The proof of the inverse function theorem is quite complex, so we will present the generic proof through a graphical method that is easy to understand. Let’s take a look at the picture below.
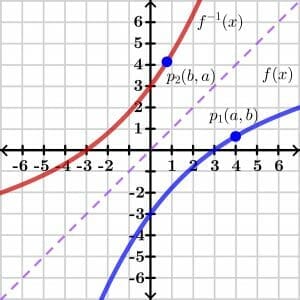
Consider two variables “$y$” and “$x$”. Here, “$y$” is the dependent variable and “x” is the independent variable, so we can write $y= f(x)$. If $y = x$, it will give us a straight linear line as represented in the picture above. The inverse of the function $f(x)$ shows the inverse graph over the opposite side of the line $y = x$ as shown in the picture.
Now consider a point “$p_1$” on graph $y = f(x)$ having coordinates $(a,b)$. For the inverse function to exist, this function should be one to one so if we take the inverse of $y = f(x)$, then the inverse function will have the mirror coordinates at point “$p_2$” $(b,a)$ as shown in the picture above.
In short, we can say that the inverse function is the mirror of the original function. For the point “$p_1$”, the function $y=f(x)$ has the coordinates $(a,b)$ so we can write $b =f(a)$ as the coordinates (a,b) show us the value of “$x$” and “$y$”. The same point on the inverse function $y = f^{-1}(x)$ has coordinates $(b,a)$ so we can write $a =f^{-1}(b)$.
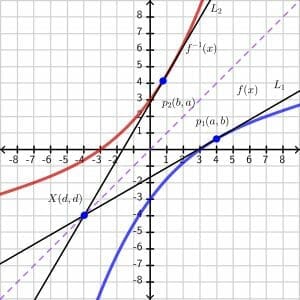
Inverse of the $b =f(a)$ can be written as $a = f^{-1}(b)$. Now if we draw the tangent line say “L_1” on the original function f(x) and a tangent line “L_2” on the inverse function, then the slope on the point “$p_1$” and “$p_2$” will give us the derivative of those points.
We can see that the lines intersect at point “$X$” on the line $y=x$. We do not know the exact coordinates of the line so let’s say the point of intersection is $(d,d)$ as shown in the second figure.
The derivative of a point on a graph is the slope of the tangent line. The formula for the slope on the tangent line can be written as:
Slope of a tanget line $= \dfrac{\Delta y}{\Delta x}$
If we take the derivative of “$x$” at point A on function $y=f(x)$
$f'(a)$ = $Slope \hspace{1mm}of\hspace{1mm} Line \hspace{1mm}L_1$ = $\dfrac{b-d}{a-d}$
If we take the derivative of “$x$” at point A on function $y=f(x)$
$(f^{-1})'(b)$ =$ Slope\hspace{1mm} of\hspace{1mm} Line\hspace{1mm} L_2 $= $\dfrac{a-d}{b-d}$
So, $Slope of L_1 = \dfrac{1}{Slope\hspace{1mm} of\hspace{1mm} L_2}$
Therefore,
$(f^{-1})'(b) = \dfrac{1}{f'(a)}$
Example 5:
Use the inverse function theorem to find the derivative of $f(x) = \dfrac{x+4}{x}$. Also, verify your answer by directly computing through differentiation.
Solution:
Let $f(x)$ be the original function and $g(x)$ be the inverse function. We know by inverse function theorem that:
$g'(x) = \dfrac{1}{f'(g(x))}$
If $f(x) = \dfrac{x+4}{x}$
Then the inverse $g(x)$ can be calculated as shown in example 3. The inverse $g(x) = \dfrac{4}{x-1}$
Then $g^{‘}(x) = \dfrac{dy}{dx} \dfrac{4}{x-1}$
$g^{‘}(x) = \dfrac{dy}{dx} (4). (x-1)^{-1}$
$g^{‘}(x) = – (4). (x-1)^{-2}$
$g^{‘}(x) = -\dfrac{4}{(x-1)^{2}}$
$g^{‘}(f(x)) = -\dfrac{4}{(f(x)-1)^{2}}$
$g^{‘}(f(x)) = -\dfrac{4}{(\dfrac{x+4}{x}-1)^{2}}$
$g^{‘}(f(x)) = -\dfrac{4}{(\dfrac{x+4}{x})^{2}+1-2(\dfrac{x+4}{x})}$
$g^{‘}(f(x)) = -\dfrac{4}{(\dfrac{x^{2}+16+8x}{x^{2}})+1-(\dfrac{2x+8}{x})}$
$g^{‘}(f(x)) = -\dfrac{4}{(\dfrac{x^{2}+16+8x+x^{2}-2x^{2}-8x}{x^{2}})}$
$g^{‘}(f(x)) = -\dfrac{4}{\dfrac{16}{x^{2}}}$
$g^{‘}(f(x)) =-\dfrac{x^{2}}{ 4}$
Then by using inverse function theorem, the derivative of $f'(x)$ can be given as:
$f'(x) = \dfrac{1}{ g'(f(x))} = -\dfrac{4}{ x^{2}}$
We can verify our answer by applying the quotient rule of differentiation on original function. The quotient rule formula for function $f(x) = \dfrac{g(x)}{h(x)}$ can be given as:
$\dfrac{d}{dx}f(x) = \dfrac{g^{‘}(x)h(x)-h^{‘}(x)g(x)}{(h(x))^{2}}$
Our given function is $f(x) = \dfrac{x+4}{x}$.
$\dfrac{d}{dx}f(x) = \dfrac{1(x)-(x+4)}{(x)^{2}}$
$f'(x) = -\dfrac{4}{ x^{2}}$
Practice Questions
1. Using the functions given below, find the inverse of the given functions. You are also required to calculate the derivative of the functions using the inverse function theorem.
- $f(x) = \dfrac{5x+2}{x}$
- $f(x) = \dfrac{6x-3}{3x}$
2. Find the inverse of the logarithmic functions given below.
- $f(x) = log(x+5)-7$
- $f(x) = log_5(x+5)-6$
Answer Keys
1.
1) Let $y=f(x)$
$y = \dfrac{5x+2}{x}$
Now swap both variables:
$x = \dfrac{5y+2}{y}$
$xy = 5y+2$
$5y = xy-2$
$5y-xy = -2$
$y(5-x) = -2$
$y = \dfrac{-2}{5-x} = \dfrac{2}{x-5}$
So,
$f^{-1}(x) = -\dfrac{2}{5-x}$
If $f(x) = \dfrac{5x+2}{x}$
Then the inverse $g(x)$ as calculated above is $g(x) = \dfrac{2}{x-5}$
$g^{‘}(x) = \dfrac{dy}{dx} \dfrac{2}{x-5}$
$g^{‘}(x) = \dfrac{dy}{dx} (2). (x-5)^{-1}$
$g^{‘}(x) = – (2). (x-5)^{-2}$
$g^{‘}(x) = -\dfrac{2}{(x-5)^{2}}$
$g^{‘}(f(x)) = -\dfrac{2}{(f(x)-1)^{2}}$
$g^{‘}(f(x)) = -\dfrac{2}{(\dfrac{5x+2}{x}-1)^{2}}$
$g^{‘}(f(x)) = -\dfrac{2}{(\dfrac{5x+2}{x})^{2}+5^{2}-(2)(5)(\dfrac{5x+2}{x})}$
$g^{‘}(f(x)) = -\dfrac{2}{(\dfrac{25x^{2}+4+20x}{x^{2}})+25-(\dfrac{50x+20}{x})}$
$g^{‘}(f(x)) = -\dfrac{2}{(\dfrac{25x^{2}+4+20x+25x^{2}-50x^{2}-20x}{x^{2}})}$
$g^{‘}(f(x)) = -\dfrac{2}{\dfrac{4}{x^{2}}}$
$g^{‘}(f(x)) =-\dfrac{x^{2}}{ 2}$
Then by using inverse function theorem, the derivative of $f'(x)$ can be given as:
$f'(x) = \dfrac{1}{ g'(f(x))} = -\dfrac{2}{ x^{2}}$
2) Let $=f(x)$
$y = \dfrac{6x-3}{3x}$
Now swap both variables:
$x = \dfrac{6y-3}{3y}$
$3xy = 6y-3$
$6y = 3xy+3$
$6y-3xy = 3$
$3y(2-x) = 3$
$y = \dfrac{3}{3(2-x)}$
So,
$f^{-1}(x) = \dfrac{1}{(2-x)}$
$f^{-1}(x) = -\dfrac{1}{(x-2)}$
If $f(x) = \dfrac{6x-3}{3x}$
Then the inverse $g(x)$ as calculated above is $g(x) = -\dfrac{1}{x-2}$
$g^{‘}(x) = \dfrac{dy}{dx} (-\dfrac{1}{x-2})$
$g^{‘}(x) = -\dfrac{dy}{dx} (1). (x-2)^{-1}$
$g^{‘}(x) = (1). (x-2)^{-2}$
$g^{‘}(x) = \dfrac{1}{(x-2)^{2}}$
$g^{‘}(f(x)) = \dfrac{1}{(f(x)-1)^{2}}$
$g^{‘}(f(x)) = \dfrac{1}{(\dfrac{6x-3}{3x}-2)^{2}}$
$g^{‘}(f(x)) = \dfrac{1}{(\dfrac{6x-3}{3x})^{2}+2^{2}-(2)(2)(\dfrac{6x-3}{3x})}$
$g^{‘}(f(x)) = \dfrac{1}{(\dfrac{36x^{2}+9-36x}{9x^{2}})+4-(\dfrac{24x+12}{x})}$
$g^{‘}(f(x)) = \dfrac{1}{(\dfrac{36x^{2}+9-36x+36x^{2}-72x^{2}+36x}{9x^{2}})}$
$g^{‘}(f(x)) = \dfrac{1}{\dfrac{1}{x^{2}}}$
$g^{‘}(f(x)) = x^{2}$
Then by using the inverse function theorem, the derivative of $f'(x)$ can be given as:
$f'(x) = \dfrac{1}{ g'(f(x))} = \dfrac{1}{ x^{2}}$
2.
1)
Let $y=f(x)$
$y = log(x+5)-7$
Now swap the places of both variables:
$x = log(y+5)-7$
$x +7 = log(y+5)$
$10^{x +7} = (y+5)$
$10^{x+7} – 6 = y$
$y = 10^{x+7} – 6$
$f^{-1}(x) = 10^{x+7} – 6$.
2) Let $y=f(x)$
$y = log_5(x+5)-6$
Now swap the places of both variables:
$x = log_5(y+5)-6$
$x + 6 = log_5(y+5)$
$5^{(x+6)}= y+5$
$2^{(x+6)} -5 = y$
$ y =2^{(x+6)} -5 $
$ f^{-1}(x) =2^{(x+6)} -5 $
