JUMP TO TOPIC
The law of cosines or cosine theorem is a rule that provides us with the relation between the sides and angles of a triangle.
The relationship is described using the formula:
$c^2 = a^2 + b^2 -2ab\cos (z)$ or $c = \sqrt{a^2 + b^2 -2ab\cos (z)}$,
where $a$, $b$ and $c$ are the three sides of the triangle and $z$ is the angle between the sides $a$ and $b$, as shown in the figure below:
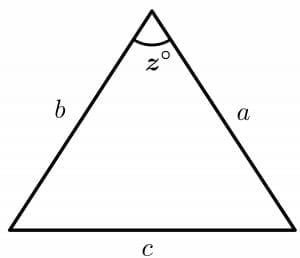
A triangle has three sides and three angles, and we use trigonometry to find the relations between the sides and angles of the triangle. For example, if we are given two sides and one angle of a triangle, the cosine theorem will help us find the unknown angle.
Similarly, if we are given the values of all the three sides of a triangle, we can use the cosine theorem to find all the three interior angles of the triangle. In this topic, we will discuss in detail the law of cosines, how they are helpful in the calculation of unknown data of a triangle, and when to use the law of cosines.
What Is the Law of Cosines?
The law of cosines is used to help us develop relations between the sides and angles of a triangle. In other words, it helps us solve the unknown or missing data related to the sides and angles of a triangle.
In trigonometric terms, the law of cosines states that the square of the length of one side of a triangle will be equal to the sum of the squares of the length of the remaining sides, while subtracting twice the product of the remaining sides multiplied by cosine angle.
Consider a triangle ABC; if we are given the values of the side “a” and “b” and the value of angle “z” between them, then the value of side “c” can be calculated using the cosine rule.
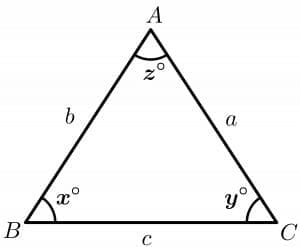
- $c^{2} = a^{2} + b^{2} – 2ab\hspace{1mm} cos( z)$
Similarly, if sides “a” and “c” along with their corresponding angle are given, then we can calculate the side “b” as:
- $b^{2} = a^{2} + c^{2} – 2ac\hspace{1mm} cos( y)$
Similarly, if we have to calculate side “a”:
- $a^{2} = b^{2} + c^{2} – 2bc\hspace{1mm} cos( x)$
Similarly, if we are given all the sides, then we can calculate the angle between any of the two sides.
- $cos (x) = \dfrac{(b^{2} + c^{2} –a^{2})}{2bc}$
- $cos (y) = \dfrac{(a^{2} + c^{2} –b^{2})}{2ac}$
- $cos (z) = \dfrac{(a^{2} + b^{2} – c^{2})}{2ab}$
When To Use Law of Cosines
The law of cosines is normally used to find an unknown side or an unknown angle of a triangle when some of the data related to the triangle is available. Precisely speaking, the law of cosines is used for the following purposes:
- To find the third side of a triangle, when the length of two sides and their corresponding interior angles are given.
- To find all the missing interior angles of a triangle when the lengths of all three sides are given.
Take note that when two angles and one side of a triangle are given, then we use the law of sines, not the law of cosines.
How To Use the Law of Cosines
The law of cosines is done to determine the missing parameters of a triangle given some required data. Let us discuss the steps of how to use the cosine rule to find the missing values of a triangle.
Step 1: Write down all the given data related to the triangle. If you are given two sides and their corresponding angles, continue to step 2, and if you are given all the sides and you have to find the angles, continue to step 3.
Step 2: Apply the cosine rule formulas:
- $a^{2} = b^{2} + c^{2} – 2bc \hspace{1mm}cos( x)$
- $b^{2} = a^{2} + c^{2} – 2ac \hspace{1mm}cos (y)$
- $c^{2} = a^{2} + b^{2} – 2ab\hspace{1mm} cos (z)$
where, a, b and c are the sides of the triangle and x, y and z are the angles between the sides bc, ca, and ab respectively.
Step 3: Apply the cosine rule formulas:
- $cos (x) = \dfrac{(b^{2} + c^{2} –a^{2})}{2bc}$
- $cos (y) = \dfrac{(a^{2} + c^{2} –b^{2})}{2ac}$
- $cos (z) = \dfrac{(a^{2} + b^{2} – c^{2})}{2ab}$
Proof of Cosine Theorem
Let us derive the formula for the law of cosines.
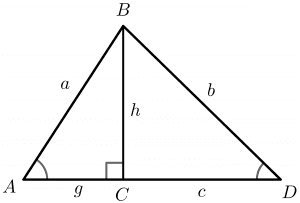
Consider the above figure for triangle ABC
$sin A = \dfrac{BC}{AB} = \dfrac{h}{a}$ (1)
and,
$cos A = \dfrac{AC}{AB} = \dfrac{g}{a}$ (2)
From equation (1) and (2), we get $h = a(sin A)$ and $g = a(cos A)$
If we apply the Pythagorean Theorem on ΔBCD,
$b^{2} = h^{2} + (c – g)^{2}$ (3)
Here, the length of “c” is greater than that of “g”.
Substituting $h = a(sin A)$ and $g = a(cos A)$ in equation (3):
$b^{2} = (a(sinA))^{2} + (c – a(cosA))^{2}$
$b^{2} = a^{2}sin^{2}A + c^{2} + a^{2}cos{2}A – 2ac·\hspace{1mm}cosA$
$b^{2} = a^{2}(sin^{2}A + cos^{2}A) + c^{2} – 2ac·\hspace{1mm}cosA$
$b^{2} = a^{2}(1) + c^{2} – 2ac·\hspace{1mm}cosA$
$b^{2} = a^{2} + c^{2} – 2bc·\hspace{1mm}cosA$
Example 1:
Consider a triangle ABC with the sides a $= 5cm$, b$ = 6cm$ and c $= 4 cm$. What will be the value of angles x, y, and z of said triangle?
Solution:
We are given the values of all three sides of the triangle and we have to calculate the value of all three angles. Using the cosines rule formula, we know that:
- $cos (x) = \dfrac{(b^{2} + c^{2} –a^{2})}{2bc}$
- $cos (y) = \dfrac{(a^{2} + c^{2} –b^{2})}{2ac}$
- $cos (z) = \dfrac{(a^{2} + b^{2} – c^{2})}{2ab}$
$cos (x) = \dfrac{(6^{2} + 4^{2} – 5^{2})}{2\times6\times4}$
$cos (x )= \dfrac{(36 + 16 – 25)}{48}$
$cos (x )= \dfrac{27}{48} $
$x = cos^{-1} (0.5625) $
$x = 55.77^{o}$
$cos (y) = \dfrac{(5^{2} + 4^{2} – 6^{2})}{2\times5\times4}$
$cos (y) = \dfrac{(25 + 16 – 36)}{40}$
$cos (y) = \dfrac{5}{40} $
$y = cos^{-1}( 0.125)$
$y = 82.82^{o}$
$cos (z) = \dfrac{(5^{2} + 6^{2} – 4^{2})}{2\times5\times6}$
$cos (z) = \dfrac{(25 + 36 – 16)}{60}$
$cos (z) = \dfrac{45}{60} $
$z = cos^{-1} (0.75)$
$z = 41.41^{o}$
Hence, the value of the three angles x, y and z are $55.77^{o}$ , $82.82^{o} $ and $41.41^{o}$.
Example 2:
The measure of two sides of a triangle are $5cm$ and $8 cm$, respectively. The angle between these two sides is $45^{o}$. Find the length of the third side of the triangle.
Solution:
We are given the values of all the two sides and their corresponding angle, and we have to find the length of the third side of the triangle.
Let side a $= 5cm$ , b $= 8cm$ and “x” $= 45^{o}$. Here, “x” is the angle between the two sides. The formula for law of cosines is given as:
$c^{2} = a^{2} + b^{2} – 2ab \hspace{1mm}cos (x)$
Here, a $= 5cm$ , b $= 8cm$ and x $= 45^{o}$
$c^{2} = 5^{2} + 8^{2} – 2\times5\times8 \hspace{1mm}cos (45)$
$c^{2} = 5^{2} + 8^{2} – 80 (0.7071)$
$c^{2} = 25 + 64 – 56.56$
$c^{2} = 32.44$
$c = \sqrt{32.44} = 5.69 cm$
Example 3:
A ladder is placed diagonally against the wall, forming a triangular shape. The distance from the foot of the ladder to the foot of the wall is $6 ft$ while the diagonal length of the ladder is $7ft$. Therefore, the angle formed at the base of the ladder is $60^{o}$. Calculate the missing length of the triangle.
Solution:
Let the distance between the base of the ladder and the base of wall AB $= 6 ft$ and the angle at point A is a $= 60^{o}$ while the length AC $= 7ft$ and we have to find the side BC.
$BC^{2} = AB^{2} + AC^{2} – 2\times AB\times AC \hspace{1mm}cos( a)$
$BC^{2} = 6^{2} + 7^{2} – 2\times5\times 8 cos (60)$
$BC^{2} = 36+49 – 80 (0.5)$
$BC^{2} = 36 + 49 – 40$
$BC^{2} = 45$
$BC = \sqrt{45} = 6.71 ft$
Example 4:
Consider a triangle garden: the length of the three sides AB, BC, and CA of the triangular garden are $4 cm$, $6 cm$, and $7 cm$, respectively. You are required to find all the angles of the triangular garden.
Solution:
We are given the values of all three sides of the triangle, and we have to calculate the value of all three angles. Let x, y, and z be the angles at points A, B, and C. Using the cosines rule formula, we can find all the angles.
- $cos (x) = \dfrac{(AB^{2} + BC^{2} – CA^{2})}{2\times AB\times BC}$
- $cos (y) = \dfrac{(BC^{2} + CA^{2} – AB^{2})}{2\times BC\times CA}$
- $cos (z) = \dfrac{(AB^{2} + CA^{2} – BC{2})}{2\times AB\times AC}$
$cos (x) = \dfrac{(4^{2} + 6^{2} – 7^{2})}{2\times 4\times 6}$
$cos (x) = \dfrac{(16 + 36 – 49)}{48}$
$cos (x) = \dfrac{3}{48} $
$x = cos^{-1} (0.0625)$
$x = 86.41^{o}$
$cos (y) = \dfrac{(6^{2} + 7^{2} – 4^{2})}{2\times6\times7}$
$cos (y) = \dfrac{(36 + 49 – 16)}{84}$
$cos (y) = \dfrac{69}{84} $
$y = cos^{-1}( 0.8214)$
$y = 33.77^{o}$
$cos (z) = \dfrac{(5^{2} + 4^{2} – 6^{2})}{2\times5\times4}$
$cos (z) = \dfrac{(25 + 16 – 36)}{40}$
$cos (z) = \dfrac{5}{40} $
$z = cos^{-1}(0.125)$
$z = 82.82^{o}$
Hence, the value of the three angles x, y and z are $41.45^{o}$ , $55.77^{o}$ and $82.82^{o}$.
Practice Questions
- A girl is standing on a top of a building, let this be point A, and two girls are standing on the floor outside of the building at point B and C. The three girls are standing in such a way that they form a triangle ABC. If length of the side AB$ = 5cm$ and BC $= 7cm$ while the angle at point B is $60^{o}$, what will be the length of the side AC?
- Allan has a triangular-shaped boundary wall across his house. He wants to fence the boundary wall with three wires system. The length of the two sides of the boundary wall is $200ft$ and $250ft$, respectively, while the angle between the sides is $30^{o}$. Calculate the total wire needed for fencing.
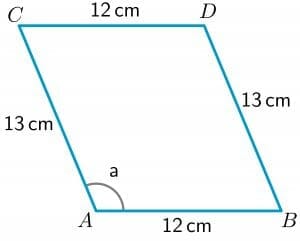
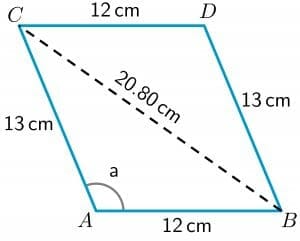
- Take a look at the parallelogram ABCD given below. The length of the sides AB , CD, BD and AC are $12cm$, $12cm$, $13 cm$ and $13 cm$, respectively. The measure of angle a $= 112.62^{o}$. Calculate the length of the diagonal BC.
Answer Key:
1. We are given the length of side AB and BC and the angle value between these two sides. So, by using the formula for the cosine rule, we can easily find the missing data for side AC.
$AC^{2} = AB^{2} + BC^{2} – 2\times AB\times AC \hspace{1mm}cos a$
$AC^{2} = 5^{2} + 7^{2} – 2\times5\times 7 \hspace{1mm}cos 60^{o}$
$AC^{2} = 25 +49 – 70 (0.5)$
$AC^{2} = 25 + 49 – 35$
$AC^{2} = 39$
$AC = \sqrt{39} = 6.24 cm$
2. We are given the length of the two sides of the triangular boundary along with the angle between the sides. Let side a = 200ft, b $= 250ft$ and angle “x” $= 30^{o}$. Let us assume the missing side is “c”. Now let’s solve for the missing side using the law of cosines.
$c^{2} = a^{2} + b^{2} – 2\times ab\times AC \hspace{1mm}cos x$
$c^{2} = 200^{2} + 250^{2} – 2\times200\times 250 cos 30^{o}$
$c^{2} = 40000 +62500 – 100000 (0.866)$
$c^{2} = 102500 – 86600$
$c^{2} = 15900$
$c = \sqrt{15900} = 126 ft$ approx.
Now we have the length of all the sides of the triangle. The total length required to fence all the boundaries is equal to the perimeter of the triangle.
Perimeter of triangle $= a+b+c = 200 + 250 + 126 = 576ft$. As we require $3$ wires for fencing, we have to multiply the perimeter with $3$.
Total wire required $= 3 \times \hspace{1mm}perimeter \hspace{1mm} of \hspace{1mm} triangle = 3 \times 576 = 1728ft.$
3. We are given the length of all the sides and the measure of angle “a.” Let us draw a diagonal from point B to C.
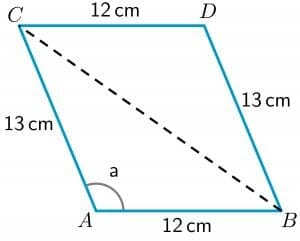
As we can see, the diagonal has divided the quadrilateral ABCD into two triangles ABC and BDC. Since we have the length of the two sides of the triangle BDC, we will calculate the length of the third side BC by using the cosine theorem.
To calculate the length of the diagonal BC, we will use the triangle ABC as we have the length of two sides of this triangle and also the value of one angle of the triangle. So the cosine formula can be written as:
$BC^{2} = AC^{2} + AB^{2} – 2\times AB\times AC cos a$
$BC^{2} = 13^{2} + 12^{2} – 2\times12 \times 13 \hspace{1mm} cos (112.62^{o})$
$BC^{2} = 169 +144 – 312 (-0.384)$
$BC^{2} = 169 + 144 +120$
$BC^{2} = 432.83$
$BC = \sqrt{252} = 20.80 cm$
Images/mathematical drawings are created using Geogebr
