Rational Root Theorem – Explanation & Examples

Rational root theorem, also known as rational zero theorem or rational root test, states that the rational roots of a single-variable polynomial with integer coefficients are such that the leading coefficient of the polynomial is divisible by the denominator of the root and the constant term of the polynomial is divisible by the numerator of the root.

Polynomials can have many variables, and the coefficients can be real numbers; however, the rational root test is only applicable to polynomials with a single variable and integer coefficients. This topic discusses rational root or zero theorems in detail, and we will also study the proof and numerical examples of the rational theorem.

What Is the Rational Root Theorem?

The rational root theorem or the rational zero test is a theorem that is used to deal with the roots of a polynomial. Roots are the values of the variable $x$ that makes the polynomial equal to zero. The degree of a polynomial tells us the number of exact roots for the given polynomial, i.e.,  the number of roots is always equal to the degree of the polynomial.

For example, the number of roots is one for a linear polynomial. For a quadratic polynomial, the number of zero roots is two, and similarly, for a cubic polynomial, the number of zero roots is three.

Rational Root Theorem Statement

Consider a polynomial equation with one variable, i.e., $f(x) = a_nx^{n}+ a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+ \cdots +a_2x^{2}+ a_1x + a_o $, where the coefficients $a_n$ to $a_o$ are all integers.

The rational root or rational zero test theorem states that $f(x)$ will only have rational roots $\dfrac{p}{q}$ if the leading coefficient, i.e., $a_n$, is divisible by the denominator of the fraction $\dfrac{p}{q}$ and the last coefficient, i.e., $a_o$, is divisible by the numerator of fraction $\dfrac{p}{q}$.

For example, consider a quadratic equation $2x^{2}+6x+ 4 = 0$. The leading coefficient “$2$” is divisible by “$1$” and “$2$” and the last coefficient “$4$” is divisible by “$1$”,” $2$” and “$4$”. So for the given equation, the factors of leading coefficient will be “$\pm{1}$” and “$\pm{2}$” and similarly, the factors of the constant term will be “$\pm{1}$”, “$\pm{2}$” and “$\pm{4}$”.

Therefore, according to the rational root theorem, the possible rational roots of the quadratic polynomial could be $\pm{1}$, $\pm{2}$, $\pm{4}$ and $\pm{1/2}$. If we solve the quadratic equation, the actual roots turn out to be “$\dfrac{-1}{2}$ and “$-1$”. Note that both roots are rational numbers and both satisfy the rational root test.

Rational Root Theorem Proof

To prove the rational root or zero theorem, let us assume that $\dfrac{p}{q}$ is a rational root for the polynomial equation $f(x) = a_nx^{n}+ a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+ ….. +a_2x^{2}+ a_1x + a_o $. Thus, $x = \dfrac{p}{q}$ satisfies the polynomial equation $f(x) = 0$. Replacing “$x$” with $\dfrac{p}{q}$ in the equation will give us:

 $ a_n(\dfrac{p}{q})^{n}+ a_{n-1}(\dfrac{p}{q})^{n-1}+a_{n-2}(\dfrac{p}{q})^{n-2}+ ….. +a_2(\dfrac{p}{q})^{2}+ a_1(\dfrac{p}{q}) + a_o = 0$

Now multiply both sides by $q^{n}$

 $ a_np^{n}+ a_{n-1}p^{n-1}q+a_{n-2}p^{n-2} q^{2}+ ….. +a_2p^{2} q^{n-2}+ a_1p q^{n-1} + a_o q^{n}  = 0$                                (1)

$a_np^{n}+ a_{n-1}p^{n-1}q+a_{n-2}p^{n-2} q^{2}+ ….. +a_2p^{2} q^{n-2}+ a_1p q^{n-1} = – a_o q^{n}$

We can see that “$p$” divides each term on the left side of the equation as we can take “$p$” as a common value on the left side of the equation.

As the L.H.S = R.H.S, we can see that “$p$” is a factor of “$a_o q^{n}$”. We proved that “$p$” is the factor of “$a_o$”, now let us prove that “$q$” is the factor of “$a_{n}$”.

 if we subtract both sides of eq (1) with “$a_np^{n}$”, we get:

 $ a_{n-1}p^{n-1}q+a_{n-2}p^{n-2} q^{2}+ ….. +a_2p^{2} q^{n-2}+ a_1p q^{n-1} + a_o q^{n} = – a_np^{n}  $

We can see that “$q$” divides each term on the left side of the equation as we can take “$q$” as a common value on the left side of the equation from each term.

As the L.H.S = R.H.S, we can see that “$q$” also divides $a_np^{n}$  or “$q$” is a factor of  “$a_n$”. With this, we proved that “$p$” is a factor of “$a_0$” and “$q$” is a factor of “$a_n$”.

Polynomials

How To Use Rational Root Theorem

Here are the steps to help you understand how to use the rational root theorem:

1. First of all, arrange the polynomial in descending order.
2. Identify the constant term in the equation and write down all its factors (positive and negative). These factors are the possible values of “p.”
3. Identify the leading coefficient and write down all its factors (positive and negative). These factors are the possible values of “q.”
4. Note down all the values of $\dfrac{p}{q}$ (positive and negative) and eliminate all the duplicate values.
5. Put the possible values of the rational roots in the polynomial equation to verify which of the possibilities make the polynomial equal to zero.
6. Use synthetic division to verify your answers. Synthetic division also helps identify the remaining non-rational roots of a polynomial, if any.

Let’s explain all these steps using an example. Consider a cubic function f(x) $= -11x^{2} + 3 x^{3}+5x – 3$.

1. First of all, arrange the polynomial in descending order, so the equation will be written as  f(x) $= 3x^{3} – 11 x^{2}+ 5x – 3$.
2. The constant term is “$3$”. The factors of “$3$” are $\pm1$ and $\pm3$. These are all the possible values of “p.”
3. The leading co-efficient is also “$3$,” so it has the same factors.
4. With this information, all the possible values of $\dfrac{p}{q}$ can be written as: When q= $\pm 1$ the possible roots can be = $\pm\dfrac{1}{1}$,$\pm\dfrac{3}{1}$ When q= $\pm 3$ the possible roots = $\pm\dfrac{1}{3}$,$\pm\dfrac{3}{3}$
5. Now remove all the duplicates in the last step, and the remaining values of “$\dfrac{p}{q}$” are the possible roots of the equation. These possible rational roots are ${\pm1}$,${\pm3}$,$\pm\dfrac{1}{3}$.
6. Now put all these possible values in the given polynomial equation f(x) $= 3x^{3} – 11 x^{2}+ 5x – 3$. The values which will make f(x) = 0 are the actual rational roots of the function. In this example, the roots are $1$, $3$ and $-\dfrac{1}{3}$.
7. Use the synthetic division method to verify the roots.

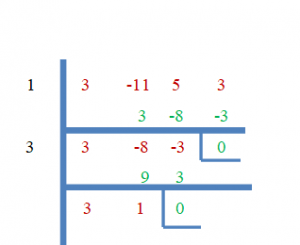
Synthetic division shows that 1 and 3 are the roots of the equation, while the remainder can be written as $3x +1 = 0$

$3x+1 = 0$

$x =  -\dfrac{1}{3}$ . Hence, the three roots of the given equations are $1$, $3$ and $-\dfrac{1}{3}$.

Important Points

This theorem is used to find the roots of a polynomial equation. Below are some important points you should remember while using this theorem.

1. All the possible rational roots are given in $\dfrac{p}{q}$ form, where “$p$” must be a factor of the constant number that is given at the last of the equation while “$q$” must be the factor of leading coefficient $a_n$.
2. The values of “$p$” and “$q$” can be negative or positive, so we have to check all $\pm\dfrac{p}{q}$ possible roots which makes the equation zero.
3. If the leading coefficient of the polynomial equation is “$1$”, then it is highly likely that the factors of the constant are also the zero roots.

Example 1: 

Determine all the possible rational roots of the polynomial function $f(x) = 6x^{3}- 8x^{2}+ 5x + 4$.

Solution:

The leading coefficient and the constant term of the given cubic function are “$6$” and “$4$,” respectively. So the factors of constant term “$4$” are $\pm{1}$,$\pm{2}$ and $\pm{4}$ while the factors of leading coefficient “$6$” are $\pm{1}$, $\pm{2}$,$\pm{3}$ and $\pm{6}$.

So the possible values of $\dfrac{p}{q}$ when $q = \pm{1}$

$\dfrac{p}{q}$ = $\dfrac{\pm1}{\pm1}$,$\dfrac{\pm2}{\pm1}$ and $\dfrac{\pm4}{\pm1}$= $\pm{1}$,$\pm{2}$, and $\pm{4}$.

when $q = \pm{2}$

$\dfrac{p}{q}$ = $\pm\dfrac{1}{2}$,$\pm\dfrac{2}{2}$ and $\pm\dfrac{4}{2}$= $\pm\dfrac{1}{2}$,$\pm{1}$ and $\pm{2}$.

when $q = \pm{3}$

$\dfrac{p}{q}$ = $\pm\dfrac{1}{3}$,$\pm \dfrac{2}{3}$ and $\pm\dfrac{4}{3}$= $\pm\dfrac{1}{3}$,$\pm\dfrac{2}{3}$ and $\pm\dfrac{4}{3}$.

when $q = \pm{6}$

$\dfrac{p}{q}$ = $\pm\dfrac{1}{6}$,$\pm \dfrac{2}{6}$ and $\pm\dfrac{4}{6}$= $\pm\dfrac{1}{6}$,$\pm\dfrac{1}{3}$ and $\pm\dfrac{2}{3}$.

Now if we eliminate the duplicates it will give us all the possible zero roots and which are $\pm\dfrac{1}{6}$,$\pm\dfrac{1}{3}$, $\pm\dfrac{1}{2}$,$\pm{1}$,$\pm\dfrac{2}{3}$,$\pm\dfrac{4}{3}$,$\pm{2}$ and $\pm{4}$.

Example 2: 

Find out the actual roots from the previous example’s given sets of possible roots. Also, verify the actual roots using the synthetic division method.

Solution:

All the values of $\dfrac{p}{q}$ that make $f(x) = 6x^{3}- 8x^{2}- 10x + 4 = 0$ are the actual roots. So let us put in all possible roots which we found in example 1 and see which of these satisfy $f(x) = 0$.

f($\dfrac{1}{6}$)   $= 6x^{3}- 8x^{2}- 10x + 4$

          $ = 6 (\dfrac{1}{6})^{3} – 8 (\dfrac{1}{6})^{2}-10(\dfrac{1}{6}) +4 \ne 0$

f($-\dfrac{1}{6}$) $=  6 (-\dfrac{1}{6})^{3} – 8 (-\dfrac{1}{6})^{2}-10(-\dfrac{1}{6}) +4 \ne 0$

f($\dfrac{1}{3}$)  $=  6 (\dfrac{1}{3})^{3} – 8 (\dfrac{1}{3})^{2}-10(\dfrac{1}{3}) +4 = 0$

         $ = \dfrac{6}{27}- \dfrac{8}{9}-\dfrac{10}{3}+4 = 0$

         $= \dfrac{(6\hspace{1mm}-\hspace{1mm}24\hspace{1mm}-90+\hspace{1mm}108)}{27}= 0$

        $= 6-24-90+108 = 0$

        $= 114-114 = 0$.

f($-\dfrac{1}{3}$) $=  6 (-\dfrac{1}{3})^{3} – 8 (-\dfrac{1}{3})^{2}-10(-\dfrac{1}{3}) +4 \ne 0$

 f($\dfrac{1}{2}$)  $=  6 (\dfrac{1}{2})^{3} – 8 (\dfrac{1}{2})^{2}-10(\dfrac{1}{2}) +4 \ne 0$

f($-\dfrac{1}{2}$) $=  6 (-\dfrac{1}{2})^{3} – 8 (-\dfrac{1}{2})^{2}-10(-\dfrac{1}{2}) +4 \ne 0$

f($1$)  $=  6 (1)^{3} – 8 (1)^{2}-10(1) +4 \ne 0$

f($-1$) $=  6 (-1)^{3} – 8 (-1)^{2}-10(-1) +4$

      $ = -6 -8 +10 +4 = -14+14 = 0 $.

f($\dfrac{2}{3}$)   $=  6 (\dfrac{2}{3})^{3} – 8 (\dfrac{2}{3})^{2}-10(\dfrac{2}{3}) +4 \ne 0$

f($-\dfrac{2}{3}$) $=  6 (-\dfrac{2}{3})^{3} – 8 (-\dfrac{2}{3})^{2}-10(-\dfrac{2}{3}) +4 \ne 0$.

f($\dfrac{4}{3}$)   $=  6 (\dfrac{4}{3})^{3} – 8 (\dfrac{4}{3})^{2}-10(\dfrac{4}{3}) +4 \ne 0$

f($-\dfrac{4}{3}$) $=  6 (-\dfrac{4}{3})^{3} – 8 (-\dfrac{4}{3})^{2}-10(-\dfrac{4}{3}) +4 \ne 0$

f($2$)   $=  6 (2)^{3} – 8 (2)^{2}-10(2) +4$

           $ = 6\times 8  -8 \times 4 – 20 +4  $

           $ = 48 – 32  – 20 +4  $

           $ = 52 – 52 = 0  $

f($-2$) $=  6 (-2)^{3} – 8 (-2)^{2}-10(-2) +4 \ne 0$

f($4$)   $=  6 (4)^{3} – 8 (4)^{2}-10(4) +4 \ne 0$

f($-4$)  $=  6 (-4)^{3} – 8 (-4)^{2}-10(-4) +4 \ne 0$

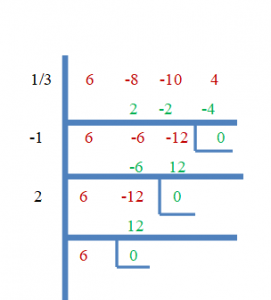
So, $\dfrac{1}{3}$, $-1$ and $2$ are the roots of $f(x) = 6x^{3}- 8x^{2}- 10x + 4$. Now let us prove this using the synthetic division method.

Example 3: 

Determine all the roots of the cubic function $f(x) = x^{3}- 6x^{2}- 8x + 16$.

Solution:

The leading coefficient in the cubic function is “$1$,” so all the possible rational roots will be the factors of the constant term “$16$”.

The factors of “$16$” can be written as: $= \pm{1},\pm{2},\pm{4},\pm{8},\pm{16}$.

Now put all these possible root values in the given function and see which root satisfies $f(x) = 0$.  

f($1$) $=  (1)^{3} – 6 (1)^{2}-8(1) +16 \ne 0$

f($-1$) $=  (-1)^{3} – 6 (-1)^{2}-8(-1) +16 \ne 0$

f($2$) $=  (2)^{3} – 6 (2)^{2}-8(2) +16 \ne 0$

f($-2$) $=  (-2)^{3} – 6 (-2)^{2}-8(-2) +16 $

              $=  -8 -24 + 16 +16 = -32 +32 = 0$

f($4$) $=  (4)^{3} – 6 (4)^{2}-8(4) +16 \ne 0$

f($-4$) $=  (-4)^{3} – 6 (-4)^{2}-8(-4) +16 \ne 0$

f($8$) $=  (8)^{3} – 6 (8)^{2}-8(8) +16 \ne 0$

f($-8$) $=  (-8)^{3} – 6 (-8)^{2}-8(-8) +16 \ne 0$

f($16$) $=  (16)^{3} – 6 (16)^{2}-8(16) +16 \ne 0$

f($-16$) $=  (-16)^{3} – 6 (-16)^{2}-8(-16) +16 \ne 0$

So “$-2$” is the only rational root we have found so far. As this is a cubic function, it will have two more zero roots. We will find the rest of the roots by using synthetic division and the quadratic equation.

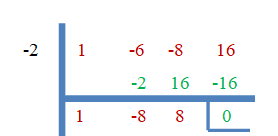
$x^{2} -8x + 8 = 0$

Solving the equation using the quadratic formula:

$x = \dfrac{-b\pm \sqrt{b^{2}-4ac}}{2a}$

here $a =1$, $b =-8$ and $c = 8 $  

$x = \dfrac{-(-8)\pm \sqrt{(-8)^{2}-4\times1 \times 8}}{2\times1}$

$x = \dfrac{8\pm \sqrt{(64-32}}{2}$

$x = 4\pm \sqrt{32}$

$x = 4\pm 4\sqrt{2}$

So, $x = 4 + 4\sqrt{2}$, $4 -2 4\sqrt{2}$. The roots of the equations are $-2$ , $4 + 4\sqrt{2}$, $4 -2 4\sqrt{2}$.

Example 4: 

Use the synthetic division method to find the value of “a” for the function $f(x) =  3x^{2} +4x – 14a$ if one of the roots is “$1$”.

Solution:

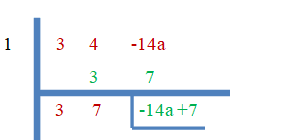
As mentioned above, “$1$” is a root of the equation, so the remainder must be zero, i.e., $-14a+7 = 0$

$-14a + 7 = 0$

$-14 a = -7$

$a = 2$

Practice Questions

1. Find the value of “b” if:

• 3 is the root of $2x^{3}-4bx^{2}+18$.
• 1 is the root of $2x^{3}-6bx +28$.

2. Solve the polynomial function if 1 and 5 are the roots $f(x)= x^{4}-21x^{2}-30 +50$.

Answer Keys

1. We know that 3 is the root, so we can easily find the value of “b” by using the synthetic division method in both parts.

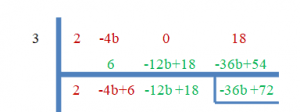
As “$3$” is the zero roots, the remainder will be equal to zero.

$-36b+72 = 0$

$b = \dfrac{-72}{-36}= 2$

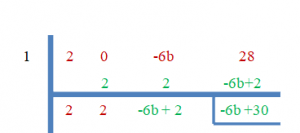
As “$3$” is the zero roots, the remainder will be equal to zero.

$-6b+30 = 0$

$b = \dfrac{-30}{-6}=5$

2. We know that $1$ and $5$ are the roots of the given polynomial equation, so let us solve the equation first by using synthetic division, and the rest of the roots will be determined using the quadratic formula.

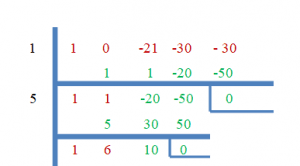
$x^{2} +6x + 10 = 0$

Solving the equation using quadratic formula:

$x = \dfrac{-b\pm \sqrt{b^{2}-4ac}}{2a}$

here $a =1$, $b = 6$ and $c = 10 $ 

$x = \dfrac{-(6)\pm \sqrt{(6)^{2}-4\times1 \times 10}}{2\times1}$

$x = \dfrac{6\pm \sqrt{(36-40}}{2}$

$x = 3\pm \sqrt{-6}$

$x = 3\pm 6i$

So, $x = 3 + 6i$, $3 + 6i$. The roots of the equations are $1$ , $5, $3 + 6i$, $3 + 6i$