Derivative of Sigmoid – Definition, Applications, and Examples

The sigmoid function, often heralded as the quintessential activation function in the realm of neural networks and deep learning, boasts an elegant S-shaped curve that smoothly transitions between 0 and 1.

We will delve deeply into the nuances of the derivative of the sigmoid function in this article, revealing its mathematical beauty and comprehending its crucial significance in the optimisation of machine learning algorithms.

Defining the Derivative of a Sigmoid 

The derivative, σ′(x), of the sigmoid function is given by:

σ′(x) = σ(x) ⋅ (1 − σ(x))

In other words, the product of the sigmoid value at that point and the difference between that sigmoid value and 1 determine the rate of change of the sigmoid function at any point x.

The sigmoid function, represented as $\sigma (x)$, is defined as:

σ(x) = 1/(1+ $e^{-x}$)​

The derivative of the sigmoid function, often used in neural network training algorithms, can be found using calculus.

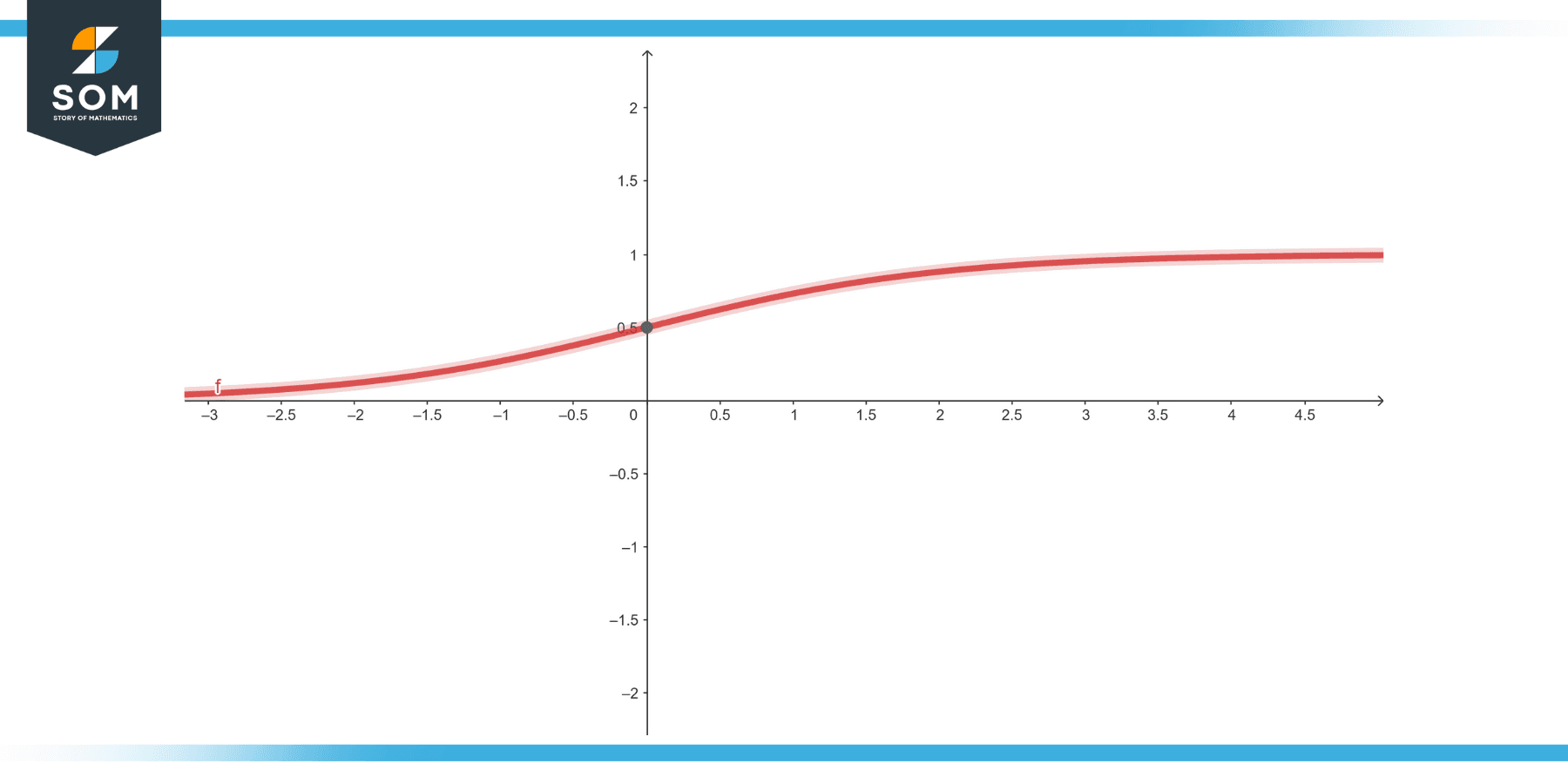
Figure-1.

This resulting derivative plays an important role in changing weights during backpropagation in neural network training and has a distinctive bell-shaped curve.

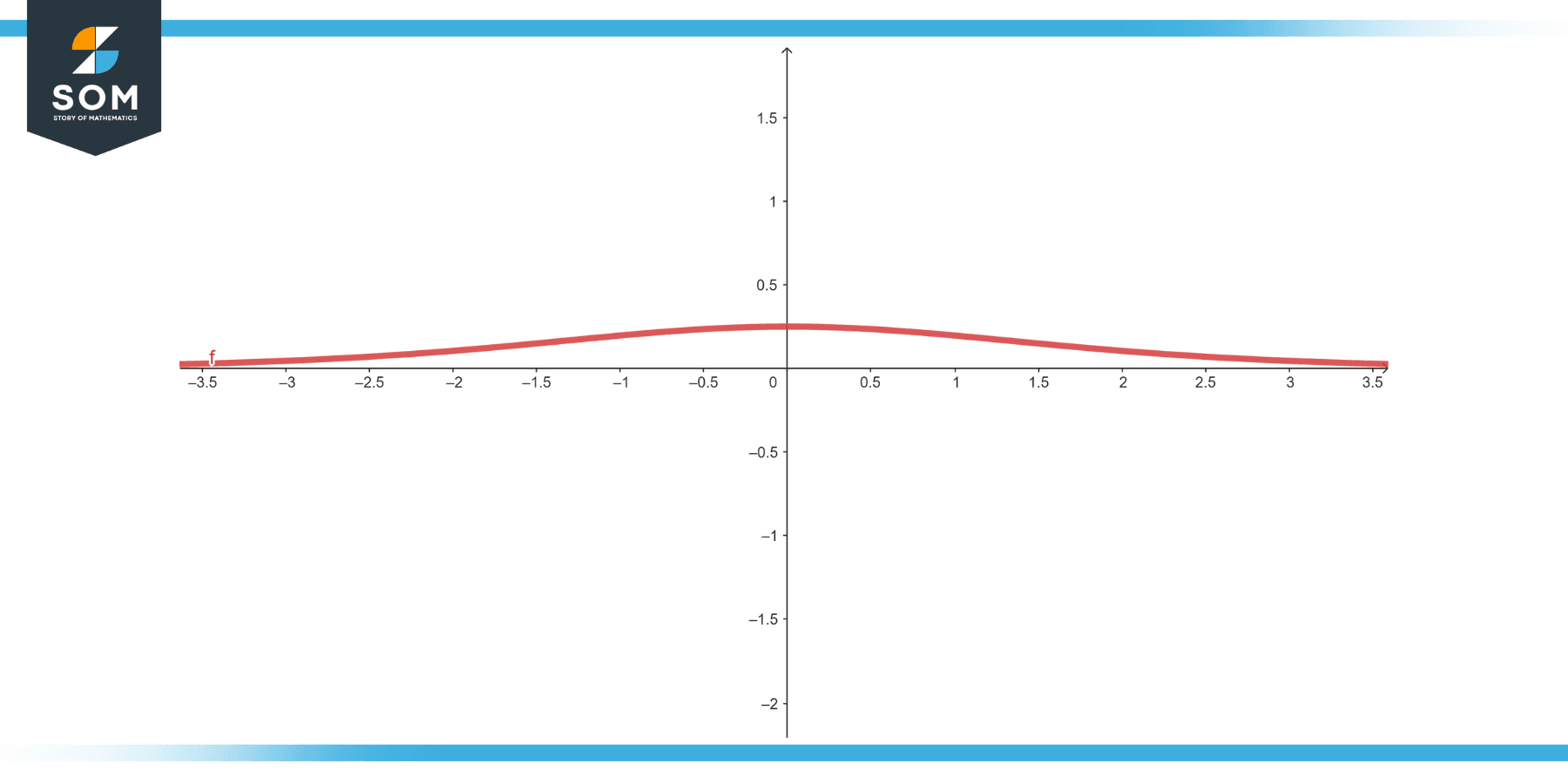
Figure-2.

Properties of Derivative of a Sigmoid

The sigmoid function’s derivative, $\sigma$′(x), possesses a number of noteworthy characteristics that are both intriguing and crucial to the function’s use in neural networks.

Definition & Expression

As previously stated, the derivative of the sigmoid function $\sigma (x)$ is given by:

σ′(x) = σ(x) ⋅ (1 − σ(x))

Range

The derivative σ′(x) has its values bounded between 0 and 0.25. This can be deduced from the range of the sigmoid function itself, which lies between 0 and 1. The maximum value of the derivative occurs at $x=0$, where σ′(0) = 0.25.

Symmetry

The derivative is symmetric about the y-axis, which means: σ′(−x) = σ′(x) This is because the sigmoid function itself is symmetric about the vertical line $x=0$.

Monotonicity

The derivative of the sigmoid function is monotonically decreasing. This means as $x$ increases, σ′(x) decreases and vice-versa.

Vanishing Gradient Problem

A significant property, particularly from a deep learning perspective, is that for values of $x$ which are large in magnitude (either positive or negative), the derivative approaches 0. This leads to the ‘vanishing gradient’ problem.

When backpropagating errors in deep networks, the weights can receive very tiny updates, essentially halting or significantly slowing down the learning. This is one reason why alternative activation functions like ReLU have been introduced.

Self-Referential Property

The derivative of the sigmoid can be expressed in terms of the sigmoid function itself. This property is advantageous from a computational perspective because if you have already computed the sigmoid output for a neuron during the forward pass, you can reuse that value to compute the gradient during the backward pass.

Smoothness

The derivative is smooth everywhere, meaning it is differentiable at every point. This property is crucial for gradient-based optimization methods like gradient descent.

Approaches Zero Asymptotically

As $x$ approaches positive or negative infinity, the derivative approaches 0. This corresponds to the regions of the sigmoid function where it starts to saturate, and changes to the input result in negligible changes to the output.

Non-zero Everywhere

Unlike some other functions (like ReLU), the derivative of the sigmoid is non-zero for all real values of $x$. This guarantees that there is always some learning going on.

Understanding these qualities is essential for machine learning, and deep learning in particular.
They impact the creation of new algorithms, new architectures, and adjustments, all with the goal of enhancing the performance of neural networks.

Exercise 

Recall

The sigmoid function, $\sigma (x)$, is defined as:

σ(x) = 1/(1+ $e^{-1}$)​

Its derivative, σ′(x), is:

σ′(x) = σ(x) ⋅ (1 − σ(x))

Example 1

Find σ′(0).

Solution

σ(0) = 1 / (1+ $e^{0}$) = 1 /2​

σ′(0) = 1 / 2​ * (1 − 1 / 2​) = 1 / 4​

Example 2

Find σ′(1).

Solution

σ(1) = 1 / (1+ $e^{-1}$)

$\sigma (1)\approx 0.7311$

σ′(1) ≈ 0.7311 * (1 − 0.7311) ≈ 0.1966

Example 3

Find σ′(−1).

Solution

σ(−1) = 1 / (1+ $e^{- (-1)}$)

$\sigma (-1)\approx 0.2689$

σ′(−1) ≈ 0.2689 * (1 − 0.2689) ≈ 0.1966

Example 4

Find σ′(2).

Solution

σ(2) = 1 / (1+ $e^{- (2)}$)

$\sigma (2)\approx 0.8808$

σ′(2) ≈ 0.8808 * (1 − 0.8808) ≈ 0.1048

Example 5:

Find σ′(−2).

Solution:

σ(−2) = 1 / (1+ $e^{- (-2)}$)

$\sigma (-2)$

σ′(−2) ≈ 0.1192 * (1 − 0.1192) ≈ 0.1048

Example 6:

Find σ′(3).

Solution:

σ(3) = 1 / (1+ $e^{- (-2)}$)

$\sigma (3)\approx 0.9526$

σ′(3) ≈ 0.9526 * (1 − 0.9526) ≈ 0.0452

Applications

The derivative of the sigmoid function plays a pivotal role in several fields, often due to its relevance to neural network training, optimization processes, and modeling of certain natural phenomena. Here’s an overview of its applications across different domains:

• Machine Learning & Deep Learning

  • Backpropagation: Perhaps the most prominent application is in training artificial neural networks using the backpropagation algorithm. The derivative of the sigmoid is used to adjust the weights of the network based on the error. Specifically, it helps in determining how much each weight contributed to the error and, thus, how it should be adjusted.
  • Gradient Descent: In gradient-based optimization techniques like gradient descent, the derivative guides the adjustment of parameters to minimize a given loss function. The sigmoid’s derivative gives the direction and magnitude of changes needed.

• Biology & Medicine:

  • Neural Modeling: The sigmoid function and its derivative have been used to model the firing rates of neurons in response to input stimuli. The sigmoid captures the idea that neurons have a threshold before they ‘fire’, and the derivative provides a measure of how sensitive the neuron is to changes in input.
  • Drug Response Modeling: In pharmacology, the sigmoidal response curve models how a change in drug dose affects a biological system’s response. The derivative helps determine the sensitivity of the system to dose changes, which is critical in drug design and administration.

• Economics & Social Sciences

  • Logistic Growth: In population dynamics, the growth of certain populations can be described by a logistic function, which is a type of sigmoid. The derivative, in this case, can provide insights into how fast the population is growing or shrinking at any given population size.
  • Economic Forecasting: The sigmoid and its derivative can be used to model certain aspects of economic growth, especially in contexts where there’s saturation or limits to growth.

• Physics & Engineering

  • Thermodynamics: In some contexts, the sigmoid function can model phase transitions, and its derivative provides insights into the sharpness of these transitions.
  • Control Systems: In systems engineering, sigmoid functions are sometimes used in controllers or system responses, and their derivatives can indicate system sensitivity to changes in input.

• Statistics

  • Logistic Regression: This is a statistical method to model binary outcomes. The sigmoid function maps any input into a value between 0 and 1, which can be interpreted as a probability. The derivative, in this context, indicates how sensitive the predicted probability is to changes in the input variables.

• Computational Neuroscience

  • Neuron Activation & Learning: Beyond the artificial neurons in machine learning, the derivative of the sigmoid function also plays a role in models of real neural networks in the brain. It can represent how the likelihood of a neuron firing changes with small adjustments to input stimuli.

All images were created with GeoGebra.