JUMP TO TOPIC

Within the expansive realm of calculus, the antiderivative, including the antiderivative of tan(x), assumes a pivotal role in solving numerous mathematical problems. When we delve into the intricacies of trigonometric functions, one of the most frequently encountered functions is the tangent function or tan(x).
Therefore, understanding the antiderivative of tan(x) broadens our grasp of integral calculus and provides a tool for solving complex equations involving this unique function.
This article aims to provide an in-depth understanding of the antiderivative of tan(x), unveiling its derivation process, properties, and real-world applications. Exploring this concept will benefit students, educators, and professionals alike in mathematics and its related disciplines.
Understanding the Tangent Function
The tangent function, commonly denoted as tan(x), is one of the six fundamental trigonometric functions. It is defined as the ratio of the y-coordinate to the x-coordinate, or in other words, the ratio of the sine to the cosine of an angle in a right triangle. Thus, we can express tan(x) = sin(x) / cos(x). It’s important to note that x is in radians for this definition.
The function tan(x) is periodic and repeats every π (or 180 degrees), meaning the values of the function are the same for x and x + π. The tangent function is not defined for certain values of x, namely x = (2n + 1)π/2, where n is any integer, since these are the points where the cosine function equals zero, leading to division by zero in the tan(x) definition.
Properties of Tangent Function
Sure, let’s delve into the properties of the tangent function or tan(x):
Periodicity
Tan(x) is a periodic function that repeats its values after an interval called the period. The period of tan(x) is π (or 180 degrees), meaning tan(x + π) = tan(x) for all values of x.
Symmetry
Tan(x) is an odd function exhibiting symmetry about the origin. In mathematical terms, tan(-x) = -tan(x). This means the function is symmetrical with respect to the origin in the Cartesian coordinate system.
Asymptotes
The function tan(x) has vertical asymptotes at x = (2n + 1)π/2 (or 90 + 180n degrees), where n is any integer. This is because these are the points where the cosine function equals zero, leading to division by zero in the tan(x) definition.
Relationship With Other Trigonometric Functions
Tan(x) is the ratio of the sine to the cosine of an angle in a right triangle. Thus, tan(x) = sin(x) / cos(x).
Range
The tan(x) range is all real numbers, meaning it can take any real value.
Increasing Function
Over any period from -π/2 to π/2 (exclusive), tan(x) is an increasing function. This means that as the input (x-value) increases, the output (y-value) increases.
Quadrantal Values
The values of tan(x) at quadrantal angles are:
- tan(0) = 0
- tan(π/2) is undefined
- tan(π) = 0
- tan(3π/2) is undefined
- tan(2π) = 0
Understanding these properties of the tangent function is critical in trigonometry, helping solve various complex problems involving angles and ratios in triangles. Furthermore, the tangent function finds extensive applications across diverse domains, including physics, engineering, computer science, and more.
Graphical Representation
The tan(x) graph consists of vertically aligned curves, called asymptotes, at the points x = (2n + 1)π/2, reflecting that the function approaches positive or negative infinity at these points. The graph rises from negative infinity to positive infinity in each period. Below is the graphical representation of the generic tan(x) function.
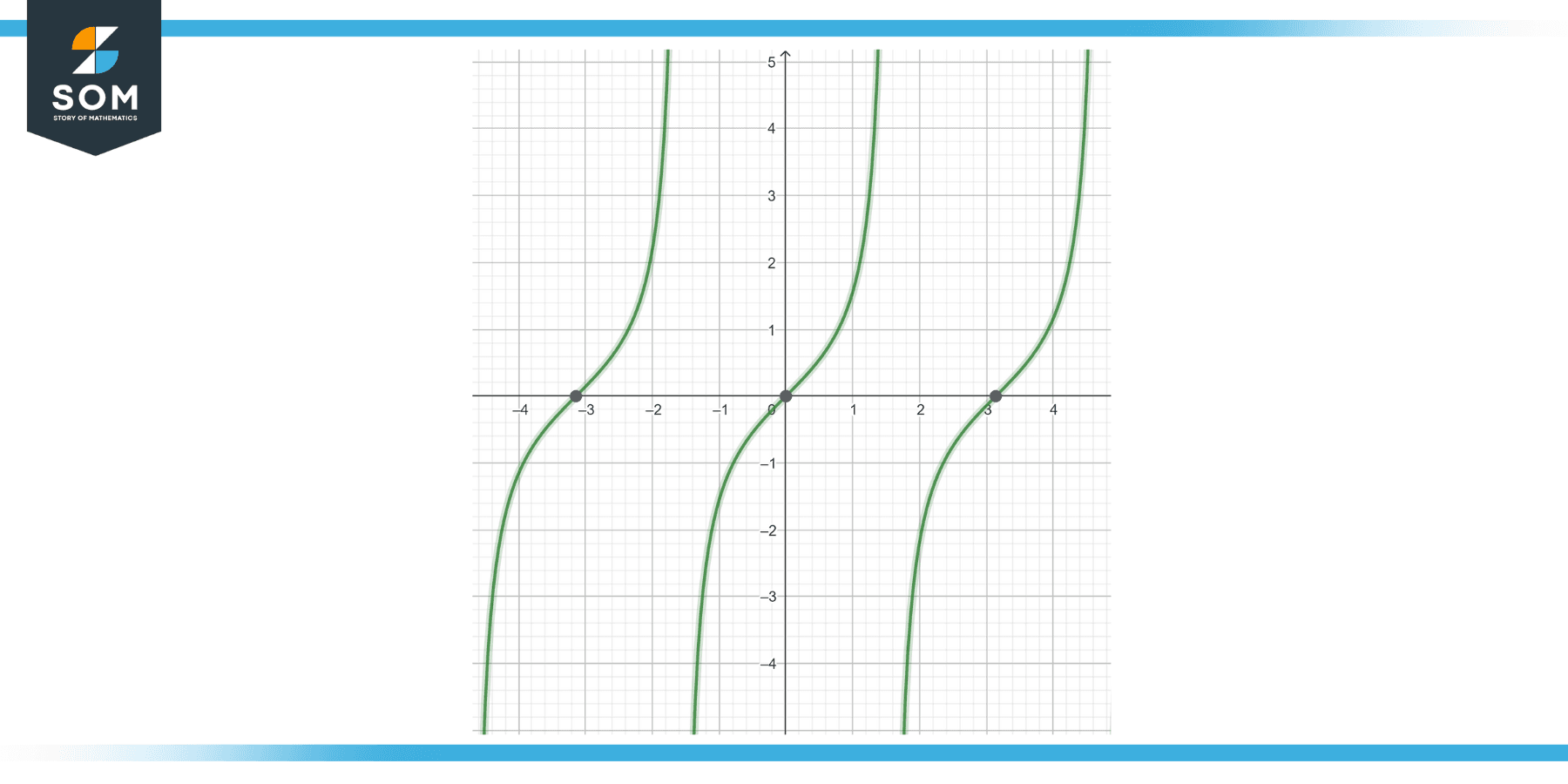
Figure-1: Generic tan(x) function.
Antiderivative of Tangent Function (tan(x))
In calculus, the antiderivative of a function is essentially the most general form of the integral of that function. When we talk about the antiderivative of the tangent function, denoted as tan(x), we refer to a function that, when differentiated, yields tan(x).
The antiderivative of tan(x) is defined as ln|sec(x)| + C, where C represents the constant of integration, and the absolute value denotes that we take the positive value of sec(x). It’s important to note that the vertical bars around sec(x) do not denote an absolute value in the traditional sense but rather a natural logarithm of the absolute value of the secant of x, which helps keep the values within the real number domain.
The aforementioned expression is derived by utilizing the properties of integration and clever algebraic manipulation, the details of which we shall explore further in this article. Below is the graphical representation of the antiderivative of the tan(x) function.
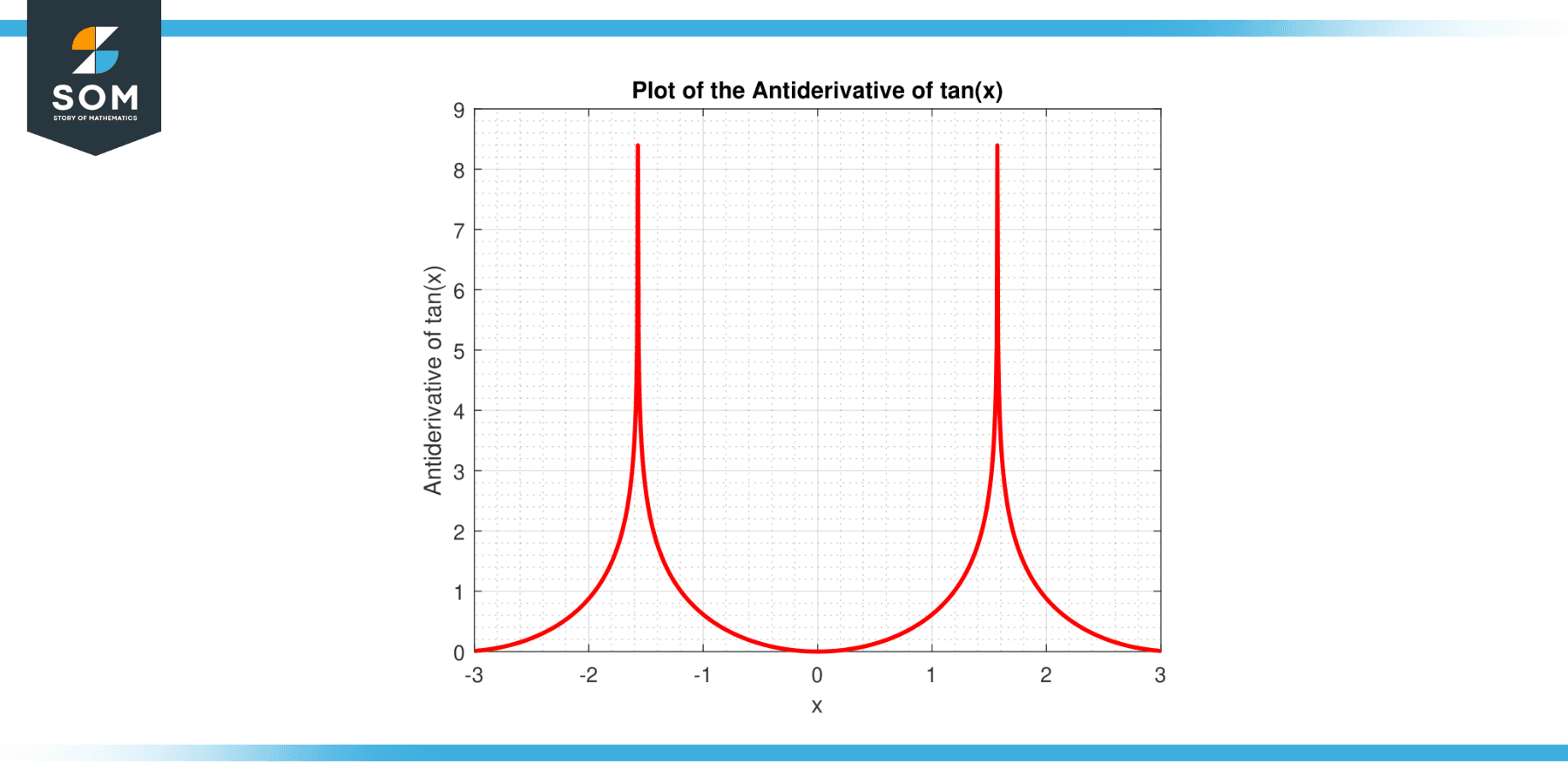
Figure-2: Antiderivative of tan(x) function.
Properties of Antiderivative of tan(x)
The antiderivative of the tangent function, denoted as ∫tan(x)dx, has some interesting properties. Let’s explore them in detail:
Non-Elementary Function
The antiderivative of tan(x) does not have a simple elementary function representation. Unlike some basic functions like polynomials or exponentials, the antiderivative of tan(x) cannot be expressed using a finite combination of elementary functions.
Periodicity
The antiderivative of tan(x) exhibits periodic behavior. The tangent function has a period of π; consequently, its antiderivative also has a period of π. This means that the integral of tan(x) repeats its values every π unit.
Discontinuous Points
The antiderivative of tan(x) has points of discontinuity due to the nature of the tangent function. At values of x where tan(x) has vertical asymptotes (e.g., x = π/2 + nπ, where n is an integer), the antiderivative has a discontinuity.
Logarithmic Singularity
One property of the tan(x) antiderivative is the presence of a logarithmic singularity. This occurs at points where tan(x) becomes infinite (vertical asymptotes), such as x = π/2 + nπ. The antiderivative contains a logarithmic term approaching negative infinity as x approaches these singular points.
Branch Cuts
Due to vertical asymptotes and the logarithmic singularity, the antiderivative of tan(x) requires branch cuts. These branch cuts are lines or intervals on the complex plane where the function is discontinuous, ensuring that the function remains single-valued.
Hyperbolic Functions
The antiderivative of tan(x) can be expressed using hyperbolic functions. By using the relationships between trigonometric and hyperbolic functions, such as tan(x) = sinh(x)/cosh(x), the antiderivative can be rewritten in terms of hyperbolic sine (sinh(x)) and hyperbolic cosine (cosh(x)) functions.
Trigonometric Identities
Various trigonometric identities can be employed to simplify and manipulate the antiderivative of tan(x). These identities include the Pythagorean identity (sin²(x) + cos²(x) = 1) and the reciprocal identity (1 + tan²(x) = sec²(x)). Using these identities can help simplify the expression and make it more manageable for integration.
Applications and Significance
The antiderivative of tan(x), represented by ∫tan(x) dx = ln|sec(x)| + C, plays a significant role in various fields of mathematics and its applications. Its significance and applications can be understood in the following contexts:
Differential Equations
The antiderivative of tan(x) is widely used in differential equations. It assists in solving first-order differential equations, which are extensively applied in physics, engineering, and biological sciences to model natural phenomena.
Physics and Engineering
The antiderivative of tan(x) is used to calculate quantities that change in a manner related to tan(x). For instance, the tangent function models periodic changes in the study of wave motion or electric circuits with periodic signals.
Area Under a Curve
In calculus, the antiderivative of a function is used to compute the area under the curve of that function. Thus, the antiderivative of tan(x) can be used to find the area under the curve y = tan(x) between two points.
Computational Mathematics
Algorithms for numerical integration often use antiderivatives. Computing the antiderivative of a function can help improve the efficiency and accuracy of numerical methods.
Probability and Statistics
In probability theory and statistics, antiderivatives are used to calculate cumulative distribution functions, which give the probability that a random variable is less than or equal to a certain value.
The significance of the antiderivative of tan(x) is essentially anchored in its ability to reverse the derivative operation. This not only aids in solving various problems involving rates of change and areas under curves but also provides a better understanding of the properties and behavior of the original function, in this case, tan(x). Therefore, it is crucial in numerous scientific, mathematical, and engineering applications.
Exercise
Example 1
Find the antiderivative of the following function: tan²(x) dx, as given in Figure-3.
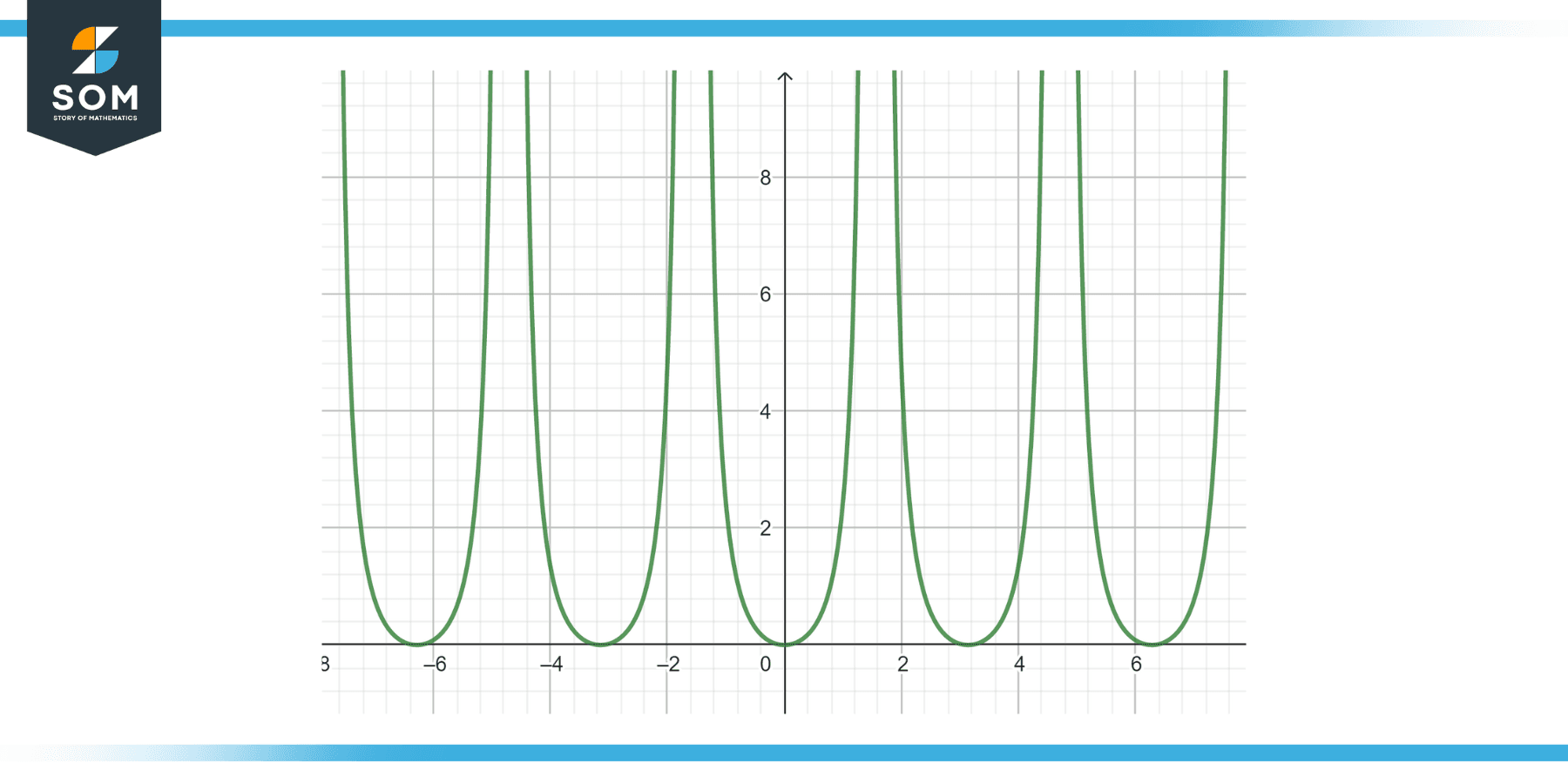
Figure-3.
Solution
To solve this integral, we can use a trigonometric identity that relates the square of the tangent function to the secant squared function. The identity is tan²(x) + 1 = sec²(x).
Rearranging the identity, we have sec²(x) – tan²(x) = 1. We can use this identity to rewrite the integral:
∫tan²(x) dx = ∫(sec²(x) – 1) dx
The integral of sec²(x) with respect to x is a well-known result, which is simply the tangent function itself:
∫sec²(x) dx = tan(x)
Therefore, we have:
∫tan²(x) dx = ∫(sec²(x) – 1) dx = tan(x) – ∫dx = tan(x) – x + C
So, the antiderivative of tan²(x) is tan(x) – x + C.
Note: The constant of integration, denoted by C, is added to account for the infinite family of antiderivatives.
Example 2
Calculate the antiderivative of the function tan(x)sec(x) dx, as given in Figure-4.
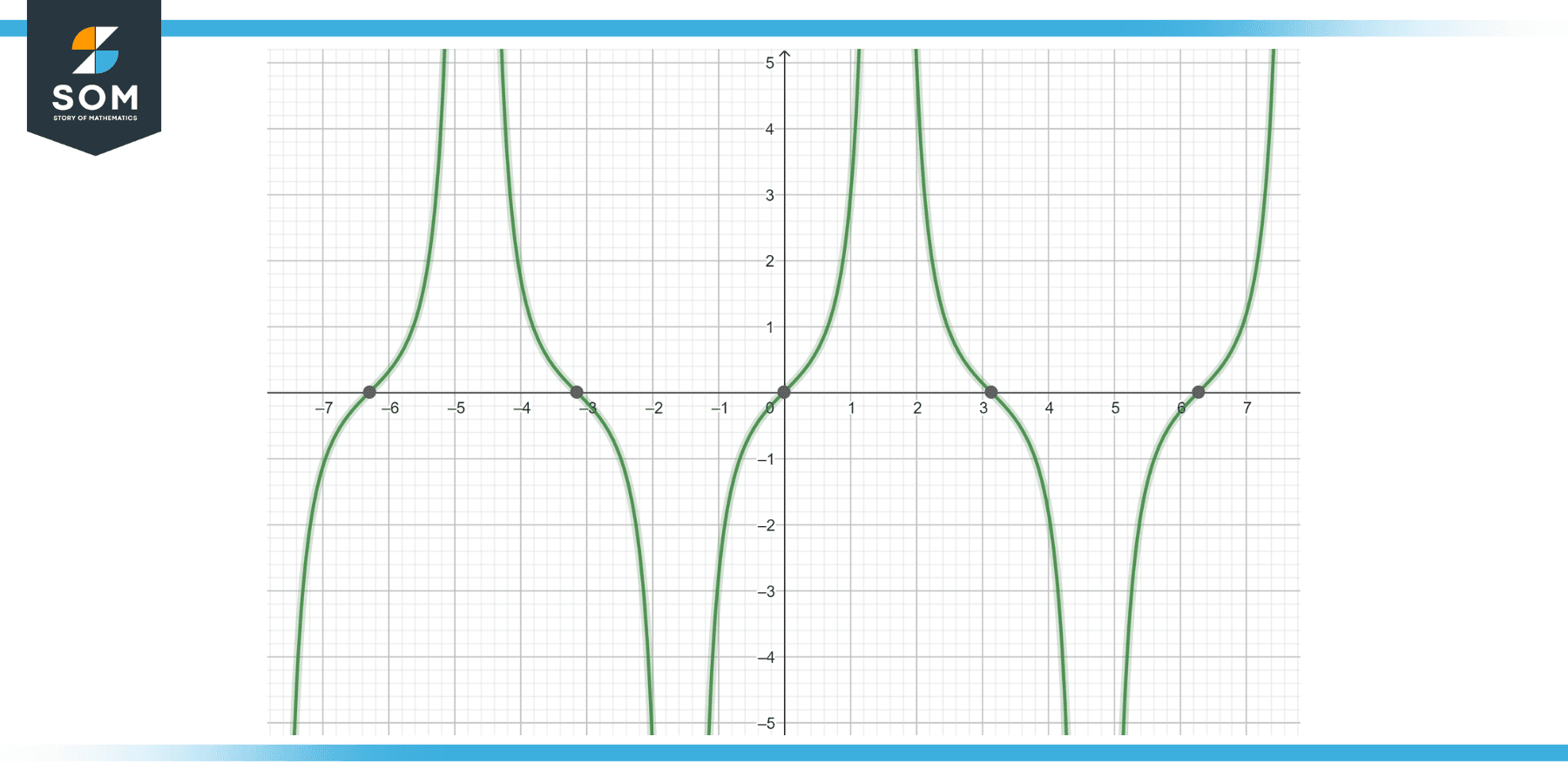
Figure-4.
Solution
To solve this integral, we can use a u-substitution. Let’s substitute u = tan(x) and find the derivative of u with respect to x:
du/dx = sec²(x)
Rearranging the equation, we have dx = du / sec²(x). Substituting these values into the integral, we get:
∫tan(x)sec(x) dx = ∫(u / sec²(x)) sec(x) du = ∫u du
Integrating u with respect to u, we have:
∫u du = (1/2) * u² + C
Substituting back u = tan(x), we obtain the final result:
∫tan(x)sec(x) dx = (1/2)tan²(x) + C
So, the antiderivative of tan(x)sec(x) is (1/2)tan²(x) + C.
Note: The constant of integration, denoted by C, is added to account for the infinite family of antiderivatives.
All figures are generated using MATLAB and Geogebra.
