In the awe-inspiring universe of mathematics and geometry, concepts extend beyond the standard three dimensions we experience daily. One such captivating idea is that of a hypersphere, an object existing in four or more dimensions, transcending our usual comprehension of space. Known as a higher-dimensional analogue of a sphere, the hypersphere represents a quantum leap in our understanding of geometric shapes and spatial dimensions.
This article will delve into the intriguing world of hyperspheres, from their fundamental mathematical representation to their significant implications in various disciplines such as computer science and theoretical physics. Whether you’re a mathematician, a curious student, or simply a knowledge enthusiast, join us as we explore the multifaceted aspects of the hypersphere – a geometrical marvel that surpasses the bounds of our traditional perception.
Definition
A hypersphere is a remarkable geometric shape defined as a higher-dimensional analogue of a sphere. It specifically refers to the collection of points in an n-dimensional Euclidean space that are equally spaced apart from a specified centre point.
Simply put, a hypersphere comprises all such points in four or more dimensions, much as a two-dimensional circle and a three-dimensional sphere consist of all points at a set distance (the radius) from a centre point. For instance, a 4-sphere, the most commonly discussed type of hypersphere, exists in four-dimensional space. Below we present generic shapes of a hypersphere.
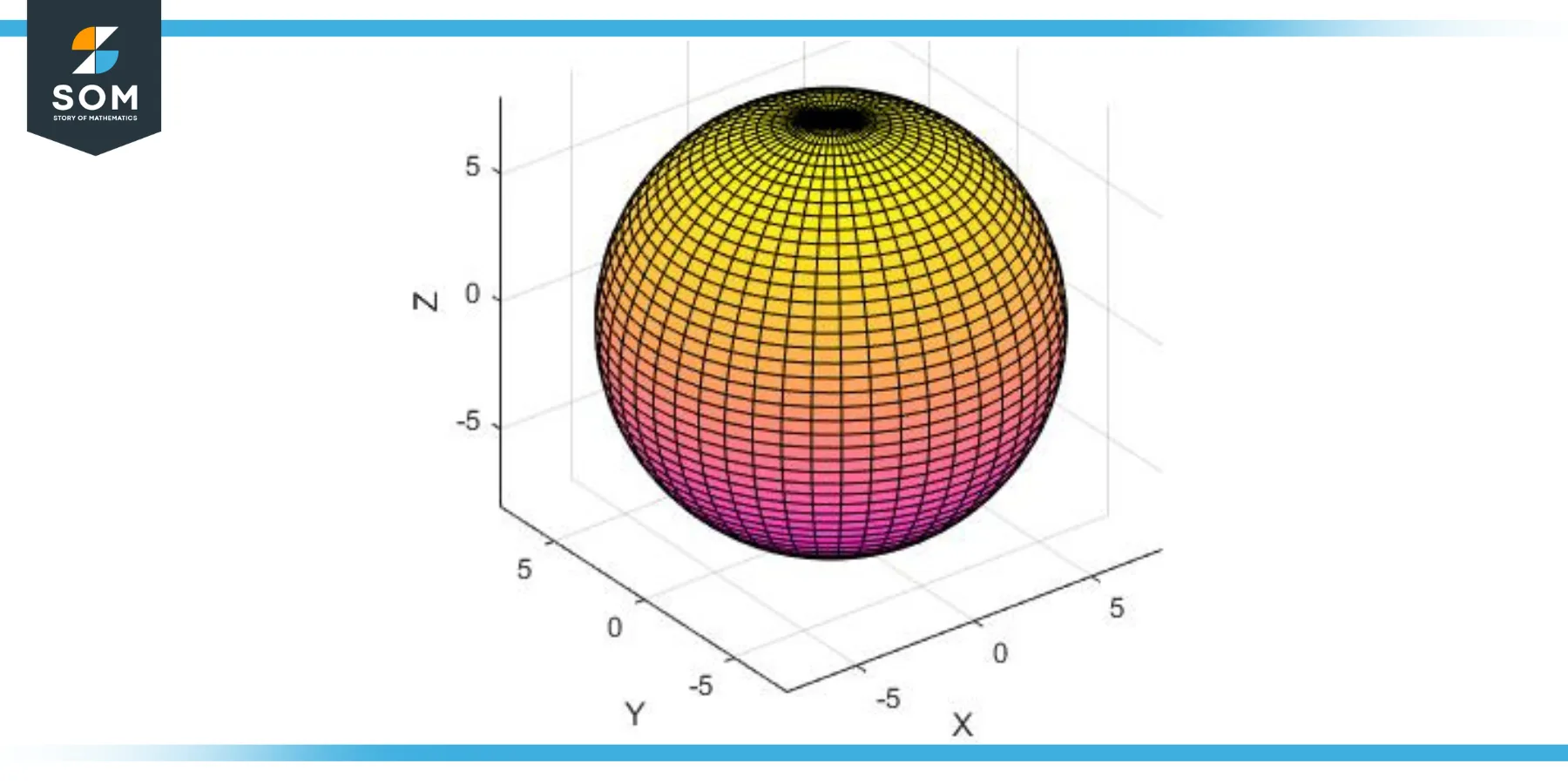
Figure-1: Generic hypersphere.
It’s important to note that the term “hypersphere” often refers to the boundary of a higher-dimensional ball, also known as an n-ball. Therefore, a hypersphere in n-dimensions is usually considered an (n-1)-dimensional surface. This fascinating geometric concept, despite its abstract nature, holds significant implications in various fields, including computer science, machine learning, and theoretical physics.
Historical Background
The concept of hyperspheres has a rich history that spans several centuries, with contributions from renowned mathematicians and physicists. Let’s explore the key milestones in the development of hypersphere theory.
Ancient Greece and Euclidean Geometry
The study of spheres and their properties can be traced back to ancient Greece. Euclid, a prominent Greek mathematician, discussed the geometry of spheres in his work “Elements” around 300 BCE. Euclidean geometry provided the foundation for understanding the properties of spheres in three-dimensional space.
Higher Dimensions and Hyperspheres
The exploration of higher-dimensional spaces began to emerge in the 19th century. Mathematicians like August Ferdinand Möbius and Bernhard Riemann made significant contributions to the field. Riemann’s work on non-Euclidean geometry opened the door to considering geometries beyond the confines of three dimensions.
Development of N-dimensional Geometry
Mathematicians started extending the ideas of spheres into greater dimensions in the late 19th century. Henri Poincaré and Ludwig Schläfli played pivotal roles in developing the field of n-dimensional geometry. Schläfli introduced the term “hypersphere” to describe the higher-dimensional analogues of spheres.
Riemannian Geometry and Curvature
The development of Riemannian geometry was made possible by the efforts of mathematician Georg Friedrich Bernhard Riemann in the middle of the 19th century. This branch of geometry deals with curved spaces, including hyperspheres. Riemann’s insights into the intrinsic curvature of surfaces and higher-dimensional spaces were instrumental in understanding the properties of hyperspheres.
Hyperspheres in Modern Physics
Theoretical physics and cosmology have embraced the concept of hyperspheres in recent decades. At the turn of the 20th century, Albert Einstein’s general theory of relativity dramatically changed how we understand gravity and the geometry of spacetime.
Hyperspheres have been used to investigate cosmic events and represent the universe’s curvature.
String Theory and Extra Dimensions
String theory became a prominent contender for a theory of everything in the late 20th century. String theorists proposed that our universe may contain more than the three spatial dimensions we observe. Hyperspheres play a crucial role in describing and visualizing these extra dimensions within the mathematical framework of string theory.
Computational Advances and Visualization
Mathematicians and physicists can now more efficiently examine hyperspheres in greater dimensions thanks to the development of powerful computers and sophisticated visualisation methods. Computer-generated visualizations and mathematical representations have aided in conceptualizing and understanding the intricate geometries of hyperspheres.
Throughout history, the study of hyperspheres has evolved alongside mathematics and theoretical physics advancements. From the foundational work of Euclidean geometry to the modern developments in string theory, hyperspheres have remained a fascinating subject of exploration, offering valuable insights into the nature of higher-dimensional spaces and their implications for our universe.
Geometry
The geometry of hyperspheres is a study in multidimensional space, which, while challenging to visualize, is rich in mathematical beauty and complexity.
Defining a Hypersphere
A hypersphere is the higher-dimensional analogue of a sphere. Similar to how a sphere is made up of all points in three-dimensional space, a hypersphere is made up of all points in n-dimensional space that are evenly spaced apart from a central point.
Coordinates and Equations
Hyperspheres are commonly represented using Cartesian coordinates. The equation for a standard n-dimensional hypersphere centered at the origin with a radius r is:
Σ(xᵢ)² = r² for i = 1, 2, …, n
Where xᵢ are the coordinates of points on the hypersphere, this equation basically states that the sum of the squares of the coordinates of any point on the hypersphere is equal to the square of the radius.
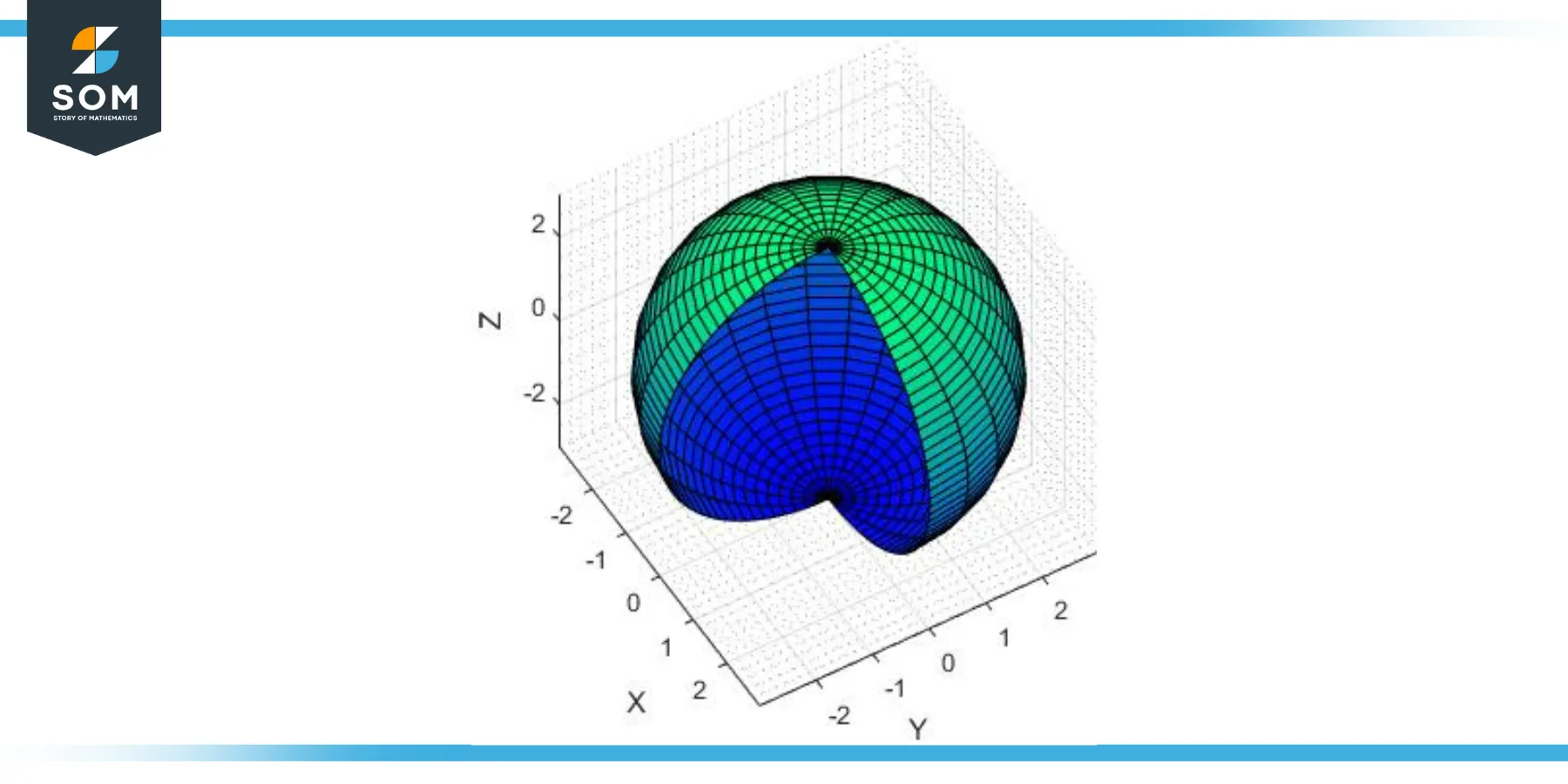
Figure-2.
Hyperspheres as Surfaces
It’s important to note that when mathematicians speak of hyperspheres, they usually refer to the boundary of the n-dimensional ball, which is an (n-1)-dimensional surface. In other words, an n-sphere is essentially a collection of (n-1)-dimensional points. For example, a 3-sphere (hypersphere in four dimensions) is a collection of 2-spheres (ordinary spheres).
The volume of a Hypersphere
The volume (or, more accurately, “content”) of a hypersphere also has an interesting relationship with its dimension. The volume of an n-ball (which includes the interior of the hypersphere) can be calculated using the formula:
$$V = \frac{\pi^{\frac{n}{2}}}{\Gamma(\frac{n}{2}+1)} \times r^n$$
where Γ represents the gamma function. As the number of dimensions increases, the volume of the hypersphere first increases but then decreases after a certain point (around the 5th dimension), which is an aspect of the “curse of dimensionality.”
Visualizing a Hypersphere
Visualizing hyperspheres is difficult due to our inability to perceive more than three dimensions, but certain techniques can be employed. For instance, a 4-dimensional hypersphere (3-sphere) can be visualized by considering a sequence of 3-dimensional cross-sections. This would resemble a sphere that grows from a point and then shrinks back to a point.
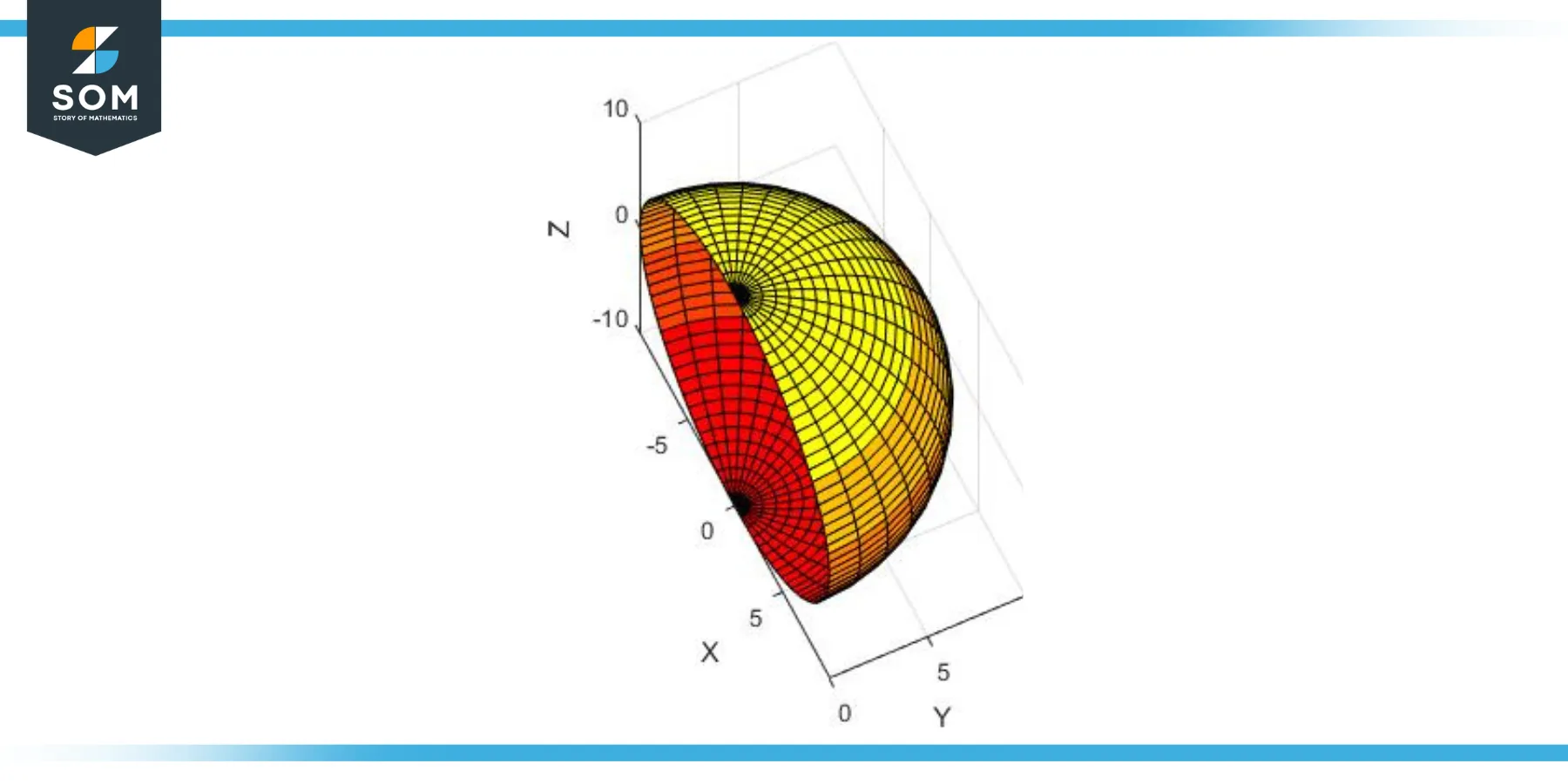
Figure-3.
Related Formulas
Equation of a Hypersphere
The general equation for an n-dimensional hypersphere, also known as an n-sphere, centered at the origin in Cartesian coordinates is:
Σ(xᵢ)² = r² for i = 1, 2, …, n
Here, r denotes the hypersphere’s radius and xᵢ denotes points on the hypersphere. According to this formula, the square of the radius equals the sum of the squares of the coordinates of any point on the hypersphere.
If the hypersphere is not centered at the origin, the equation becomes:
Σ(xᵢ – cᵢ)² = r² for i = 1, 2, …, n
Here, cᵢ are the coordinates of the center of the hypersphere.
The volume of a Hypersphere
The formula for the volume (technically referred to as “content”) of an n-ball (the region bounded by a hypersphere) is given by:
$$V = \frac{\pi^{\frac{n}{2}}}{\Gamma(\frac{n}{2}+1)} \times r^n$$
In this equation, Γ refers to the gamma function, a function that generalizes factorials to non-integer values. This formula reveals that as the dimension of the hypersphere increases, the volume first increases but then begins to decrease after the 5th dimension due to the characteristics of the gamma function and $\pi^{\frac{n}{2}}$. This phenomenon is referred to as the “curse of dimensionality.”
Surface Area of a Hypersphere
The surface area of a hypersphere, technically referred to as the “(n-1)-volume”, is given by the derivative of the volume of an n-ball with respect to the radius:
$$A =n \times \frac{\pi^{\frac{n}{2}}}{\Gamma(\frac{n}{2}+1)} \times r^{n-1}$$
This equation shows that the surface area also exhibits similar behavior to the volume with respect to the dimension of the hypersphere, first increasing but then decreasing beyond the 7th dimension.
These formulas lay the groundwork for the mathematical study of hyperspheres, allowing us to calculate fundamental properties like their volume and surface area. It’s fascinating to see how these formulas echo and extend the ones we are familiar with for two-dimensional circles and three-dimensional spheres, revealing a deep unity in geometry across dimensions.
Applications
While the concept of a hypersphere may initially seem abstract or even esoteric, it actually finds numerous practical applications across a wide range of fields.
Computer Science and Machine Learning
In computer science and particularly in machine learning, hyperspheres play a significant role. The use of high-dimensional spaces is commonplace in these fields, especially in the context of vector space models. In these models, data points (such as text documents or user profiles) are represented as vectors in a high-dimensional space, and the relationships between them can be examined using geometric concepts, including hyperspheres.
In nearest-neighbor search algorithms, hyperspheres are used to define search boundaries within these high-dimensional spaces. The algorithm will search for data points lying within a hypersphere of a certain radius centered on the query point.
Similarly, in support vector machines (SVMs), a common machine learning algorithm, hyperspheres are used in the process of kernel trick, which transforms data into higher-dimensional space to facilitate the finding of optimal boundaries (hyperplanes) between different classes of data points.
Physics and Cosmology
Hyperspheres also hold fascinating applications in the realm of physics and cosmology. For instance, they’re used in the Friedmann-Lemaitre-Robertson-Walker (FLRW) model, the standard model of Big Bang cosmology. In some variations of this model, the universe is considered to have a hyperspherical shape.
Moreover, hyperspheres come into play in the world of string theory. In string theory, our universe is proposed to have additional compact dimensions that may take the shape of a hypersphere. These extra dimensions, though unobserved in our day-to-day lives, could have profound implications for the fundamental forces of nature.
Mathematics and Topology
In pure mathematics and topology, the study of hyperspheres and their properties often leads to the development of new theories and techniques. For instance, the Poincaré conjecture, one of the seven Millennium Prize Problems, involves the properties of 3-spheres, or hyperspheres, in four dimensions.
Exercise
Example 1
Volume of a 4-Sphere
Next, let’s look at how to compute the volume of a 4-sphere. The formula for the volume of a hypersphere (specifically, the n-ball that it bounds) in n dimensions is:
$$V = \frac{\pi^{\frac{n}{2}}}{\Gamma(\frac{n}{2}+1)} \times r^n$$
Here, Γ represents the gamma function. For a 4-sphere (which is the boundary of a 5-ball) with radius 1, we substitute n=5 and r=1 into this formula:
$$V = \frac{\pi^{\frac{5}{2}}}{\Gamma(\frac{5}{2}+1)}$$
The Gamma function Γ(5/2 + 1) simplifies to Γ(7/2) = 15/8 × √(π), so the volume becomes:
$$V = \frac{\pi^{\frac{5}{2}}}{(\frac{15}{8} \times \sqrt{\pi})}$$
V = 8/15 × π²
V ≈ 5.263789
This tells us that a 4-sphere with a radius of 1 has a volume of approximately 5.263789.
Example 2
Surface Area of a 4-Sphere
Now, let’s compute the surface area of the 4-sphere. The surface area of a hypersphere in n dimensions is given by:
$$A =n \times \frac{\pi^{\frac{n}{2}}}{\Gamma(\frac{n}{2}+1)} \times r^{n-1}$$
For a 4-sphere with radius 1, substituting n=5 and r=1, we get:
$$A =5 \times \frac{\pi^{\frac{5}{2}}}{\Gamma(\frac{5}{2}+1)}$$
Simplifying the Gamma function: Γ(5/2 + 1) = Γ(7/2) = 15/8 × √(π), we find the surface area to be:
$$A =5 \times \frac{\pi^{\frac{5}{2}}}{(\frac{15}{8} \times \sqrt{\pi})}$$
This calculation tells us that a 4-sphere with a radius of 1 has a surface area of approximately 41.8879.
All images were created with GeoGebra.