JUMP TO TOPIC
Delving into the realm where patterns, functions, and behaviors take the forefront, we explore how to find end behavior in mathematics. An intriguing notion is ‘end behavior,’ deeply ingrained in mathematical analysis and calculus.
This term provides us with a window into the future trajectory of a function, depicting the path it will take as its inputs inch ever closer toward the extremes of infinity.
The article will explore the concept in depth, spotlight its practical applications, and demonstrate how it is a potent tool for mathematicians, engineers, and scientists.
How to Find the End Behavior
To find the end behavior of a polynomial function, examine the highest-degree term. The sign and degree of this term will determine the behavior of the function as x approaches positive or negative infinity.
In mathematics, ‘end behavior‘ refers to the values a function approaches as its input (or the independent variable) heads toward positive or negative infinity. It provides insights into how a function behaves in its domain’s extremes or ends.
This behavior is particularly vital in studying limits, asymptotes, and infinite behavior of functions. Typically described using limit notation, the end behavior of a function can convey its growth or decay patterns and how it behaves ‘at the ends,’ giving us a crucial perspective on the function’s overall behavior and potential practical applications.
Understanding the End Behavior
Understanding end behavior in mathematics is about grasping how a function behaves as its input (often denoted as x) approaches positive or negative infinity. It is essentially a way to describe a function’s long-term behavior or trends. In simpler terms, it tells us what happens to a function’s output (or y-values) as the input becomes very large (either positively or negatively).
The end behavior of a function is primarily determined by its highest degree term (in polynomial functions) or by the ratio of the degrees of the numerator and denominator (in rational functions). Here are some rules that can help in understanding the end behavior of different types of functions:
Polynomial Functions
If the degree of the polynomial is even, then the function’s ends will either point up or both points down, depending on the sign of the leading coefficient. If the degree is odd, then if the leading coefficient is positive, the function will start low (as x approaches negative infinity) and end high (as x approaches positive infinity). If the leading coefficient is negative, the function will start high and end low. Below we present a generic polynomial function in Figure-1.
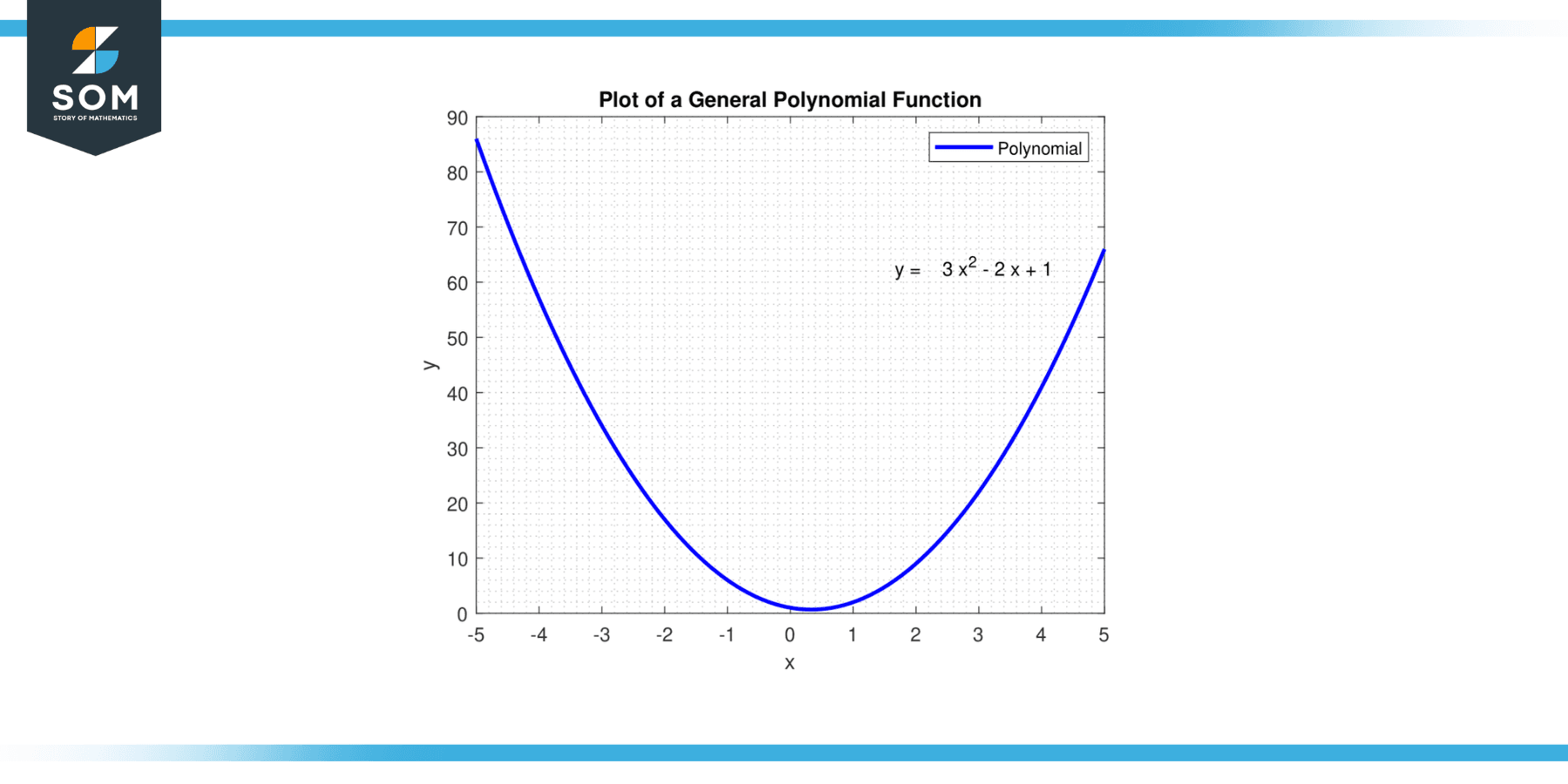
Figure-1. Generic polynomial function.
Rational Functions
If the degree of the numerator is less than the degree of the denominator, the function approaches 0 as x approaches positive or negative infinity. If the degrees are equal, the end behavior is the ratio of the leading coefficients. If the degree of the numerator is greater than the degree of the denominator, the function approaches positive or negative infinity as x approaches positive or negative infinity, depending on the coefficients’ signs. Below we present a generic rational function in Figure-2.
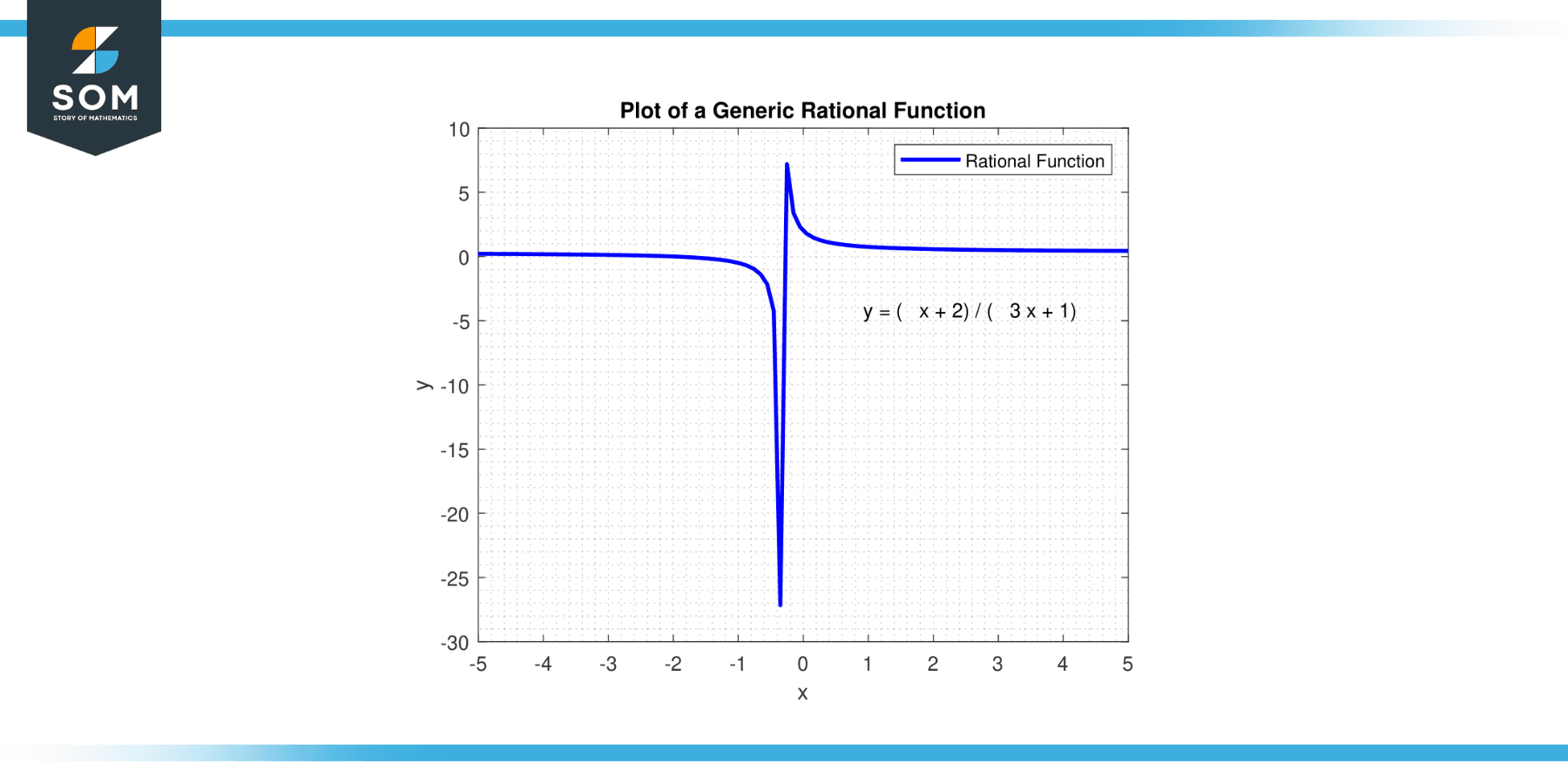
Figure-2. Generic rational function.
Exponential Functions
For exponential functions, if the base is greater than 1, the function approaches infinity as x approaches infinity and 0 as x approaches negative infinity. If the base is a fraction between 0 and 1, the function approaches 0 as x approaches infinity and infinity as x approaches negative infinity. Below we present a generic exponential function in Figure-3.
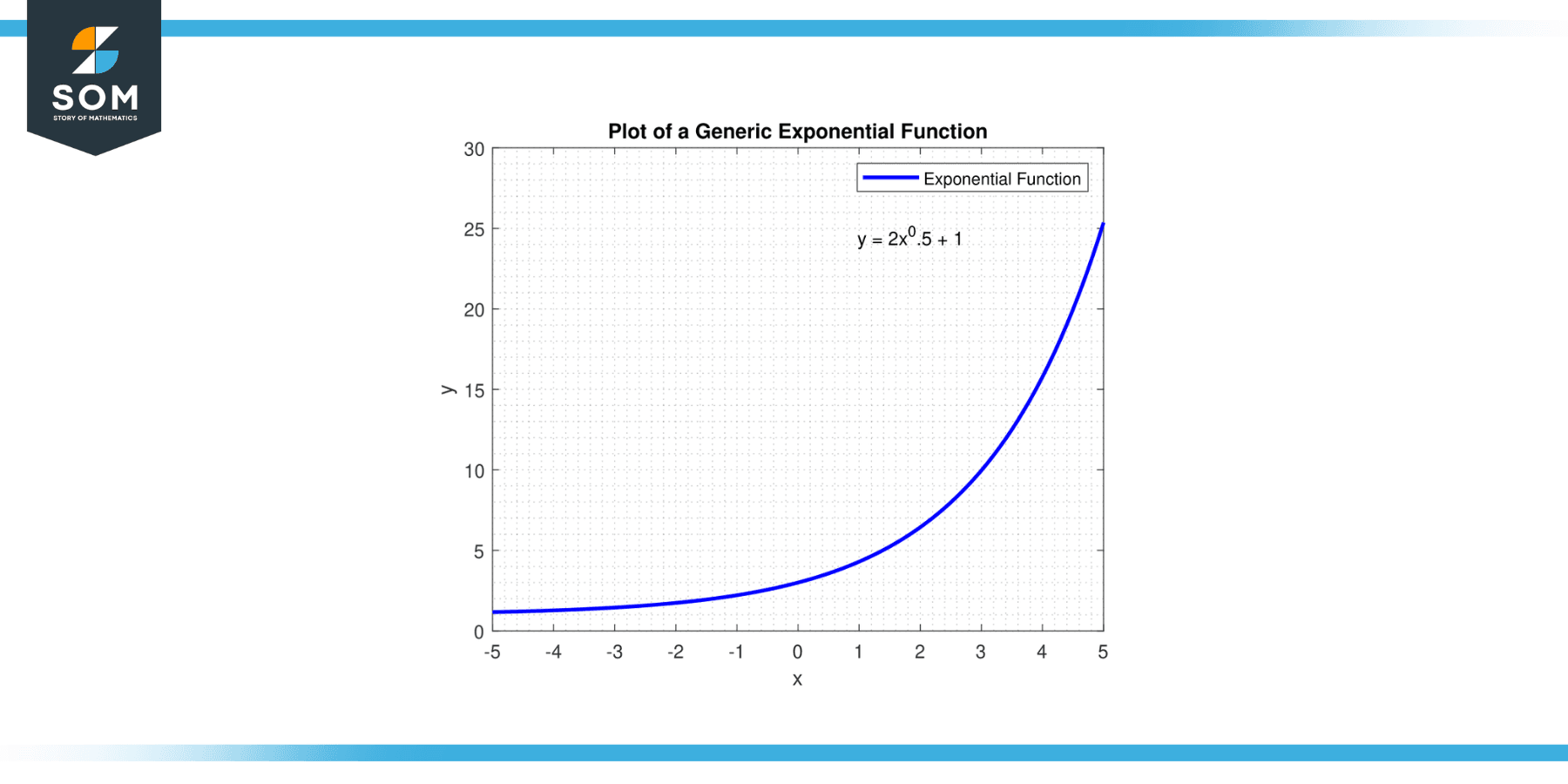
Figure-3. Generic exponential function.
Understanding the end behavior of a function is an important concept in calculus and many other branches of mathematics, and it has numerous real-world applications in fields such as physics, economics, and computer science.
Process of How to Find End Behavior
Finding the end behavior of a function typically involves analyzing its degree and leading coefficient. This is commonly done with polynomial functions, but the concept can apply to other functions. Here is a general process:
Identify the Type of Function
It’s important to recognize the type of function you’re working with, as different functions have different methods to find their end behavior. For polynomials, you’ll look at the highest power term (degree) and its leading coefficient.
Determine the Degree of the Function
For polynomial functions, the degree is the highest power of the variable within the function. The degree of the function can tell us whether the function ends up or down as we read from left to right.
Identify the Leading Coefficient
Correct, the leading coefficient is the term’s coefficient with the highest degree in a polynomial function. The leading coefficient can tell us whether the function is positive or negative as we move toward infinity.
Analyze the End Behavior
Based on the degree and leading coefficient, we can make the following conclusions:
- If the degree is even, and the leading coefficient is positive, the end behavior is: as x approaches positive or negative infinity, y approaches positive infinity. In simple terms, both ends of the graph point upwards.
- If the degree is even, and the leading coefficient is negative, as x approaches positive or negative infinity, y approaches negative infinity. Both ends of the graph point downwards.
- If the degree is odd, and the leading coefficient is positive, x approaches negative infinity, y approaches negative infinity, and as x approaches positive infinity, y approaches positive infinity. The graph falls to the left and rises to the right.
- If the degree is odd, and the leading coefficient is negative, x approaches negative infinity, y approaches positive infinity, and as x approaches positive infinity, y approaches negative infinity. The graph rises to the left and falls to the right.
It’s important to note that these rules apply to polynomial functions. Different rules or techniques may be needed to determine end behavior for other functions, such as rational, exponential, or logarithmic functions.
Properties
Understanding the end behavior of a function provides insights into its behavior as it approaches infinity in the positive or negative direction. Here are some essential properties of end behavior that are crucial for analysis:
End Behavior of Polynomial Functions
As mentioned earlier, the end behavior of polynomial functions is determined by the function’s degree and leading coefficient. If the degree is even, the end behavior of the function will be the same in both directions (both arms of the graph either point upwards or downwards). If the degree is odd, the end behavior of the function will be different in both directions (one arm of the graph points upwards, and the other points downwards).
End Behavior of Rational Functions
A rational function is a function that can be expressed as a fraction of two polynomials. The end behavior of a rational function depends on the degrees of the numerator and denominator polynomials.
- If the degree of the numerator is larger, the function approaches positive or negative infinity as x approaches positive or negative infinity.
- If the degrees of the numerator and denominator are the same, the function approaches the ratio of the leading coefficients of the numerator and denominator.
- If the degree of the denominator is larger, the function approaches 0 as x approaches positive or negative infinity.
End Behavior of Exponential Functions
For exponential functions, the end behavior depends on whether the base is greater than one or between zero and one.
- If the base is greater than one, the function approaches infinity as x approaches infinity and zero as x approaches negative infinity.
- Conversely, if the base is between zero and one, the function approaches zero as x approaches infinity and approaches infinity as x approaches negative infinity.
End Behavior of Logarithmic Functions
For logarithmic functions, as x approaches positive infinity, the function also approaches positive infinity. However, the function approaches negative infinity as x approaches zero from the right.
End Behavior of Trigonometric Functions
Trigonometric functions like sine and cosine do not have end behaviors in the conventional sense. These functions oscillate between fixed values and do not approach infinity or negative infinity as x increases or decreases. They exhibit periodic behavior instead of approaching specific values at the ends of the graph.
End Behavior and Limits
The concept of limits is heavily tied to end behavior. The end behavior is often described using limit notation, which precisely describes the behavior of a function as it approaches a particular value or infinity.
End Behavior and Asymptotes
Horizontal and slant asymptotes describe the end behavior of a function. An asymptote is a line that the function approaches but never quite reaches. The existence and direction of asymptotes can provide valuable insights into the function’s end behavior.
These properties of end behavior serve as crucial analytical tools to understand the behavior of functions towards the ends of their domains, guiding mathematical, engineering, or scientific problem-solving.
Significance
Understanding the end behavior of functions in mathematics is critical for several reasons:
Predicting Long-term Trends
The end behavior of a function helps us understand what happens to the function as the input values get very large or very small, in other words, what happens “in the long run”. This is particularly useful in fields such as physics, economics, or any area where modeling and prediction over extended periods or large ranges is required.
Analyzing the Behavior of Complex Functions
Often, complex functions are difficult to analyze due to their structure. Studying the end behavior can provide valuable insight into the overall behavior of the function, aiding in its understanding and interpretation.
Helping Determine Function Type
The end behavior can also provide clues about the type of function. For instance, even-degree polynomials have the same end behavior at positive and negative infinity, whereas odd-degree polynomials have different end behavior at positive and negative infinity.
Assessing Function Asymptotes
In rational functions, by comparing the degrees of the polynomial in the numerator and the denominator, we can predict the end behavior, which in turn helps us identify horizontal or slant asymptotes.
Comparing and Classifying Functions
The study of end behavior allows us to compare different functions and classify them according to their behavior as the input approaches infinity. This is a fundamental part of the study of algorithmic complexity in computer science, where functions are classified based on how their runtime grows as the size of the input increases.
Limit Calculations
End behavior is directly related to limits at infinity, an important concept in calculus. This is key to understanding concepts like continuity, differentiability, integrals, and series.
By understanding end behavior, mathematicians and scientists can better understand the characteristics of different functions and apply this knowledge to solve complex problems and make predictions.
Limitations of End Behavior
While the concept of end behavior is a powerful tool in mathematical analysis, it does come with its set of limitations:
Not All Functions Have Defined End Behavior
Some functions, like periodic functions (sine and cosine), do not have an end behavior in the traditional sense as they oscillate between two fixed values and never approach positive or negative infinity.
Inapplicable for Discontinuous Functions
For functions that are discontinuous or undefined at some points, the concept of end behavior might not provide a clear understanding of the function’s behavior.
Limitations With Complex Functions
When dealing with complex functions, determining end behavior can be more challenging as these functions might have different behaviors in different directions approaching infinity.
Lack of Information on Local Behavior
The end behavior gives us insights into the behavior of a function as it approaches positive or negative infinity. Still, it tells us little about what happens in the middle, also known as the local behavior of the function. Thus, it cannot be used as the sole tool to understand a function completely.
Infinite Oscillations
In some cases, functions can oscillate infinitely as they approach a limit, making it difficult to discern a clear end behavior. An example is the function f(x) = sin(1/x) as x approaches 0.
Inability to Handle Ambiguity
In certain situations, the end behavior of a function may be ambiguous or undefined. For instance, the function 1/x² oscillates between positive and negative infinity as x approaches 0.
Thus, while end behavior is an important tool for understanding how functions behave as they approach infinity, it is not a universal solution. It must be used with other analytical tools to provide a more comprehensive understanding of a function.
Applications
The concept of end behavior in mathematics has numerous applications in various fields and real life. By examining the end behavior, we can better understand various phenomena. Here are some examples:
Physics and Engineering
In physics, end behavior can be used to model and predict the behavior of physical systems. For instance, an engineer designing a bridge might use polynomial functions to model the stresses on different bridge parts. Understanding the end behavior of these functions can help predict what will happen under extreme conditions, like high winds or heavy loads.
Economics and Finance
In economics, end behavior is often used to create models to predict future trends. Economists can use functions to model data like inflation rates, economic growth, or stock market trends. The end behavior of these functions can indicate whether the model predicts ongoing growth, eventual stagnation, or cyclical behavior.
Environmental Science
In environmental science, end behavior can be used to predict the outcome of certain phenomena. For example, a model might use a function to represent the population growth of a species. The end behavior of this function can give insights into whether the population will eventually stabilize, continue growing indefinitely, or oscillate in size.
Computer Science
In computer science, especially in algorithm analysis, end behavior is used to describe the time complexity of an algorithm. By examining the end behavior of a function representing the algorithm’s runtime, one can infer how the algorithm will perform as the input size approaches infinity.
Real-life scenarios
In real life, understanding end behavior can help predict various phenomena. For example, a business owner might use a function to model their sales over time. By studying the end behavior, they can predict whether their sales will increase, decrease, or stay the same long-term.
Medicine and Pharmacology
End behavior is crucial in modeling the rate at which a drug is metabolized in the body or how the concentration of a medication changes over time in the bloodstream. As such, understanding the end behavior of the relevant functions can help physicians determine the right dosage and frequency of medication for patients.
Meteorology
In meteorology, functions may be used to model weather patterns or atmospheric conditions over time. The end behavior of these functions can provide insights into long-term climate trends or potential extreme weather events.
Population Dynamics
In biology and ecology, end behavior is used in population dynamics models. By understanding the end behavior of these models, scientists can predict whether a species’ population will grow indefinitely, stabilize, or eventually become extinct. This is particularly useful in conservation efforts for endangered species.
Astrophysics
The concept of end behavior is also used in astrophysics. For example, functions may describe a star’s lifecycle or the universe’s expansion. The end behavior of these functions provides insights into the future state of these celestial objects or systems.
Market Research
Companies use end behavior to forecast past sales or market data trends. It helps them in strategic planning, like when to launch new products, enter new markets, or phase out old services.
Agriculture
Farmers and agricultural scientists use models that involve end behavior to predict crop yields based on various factors such as rainfall, fertilizer use, and pest infestations. Understanding these models’ end behavior can help develop strategies for increasing productivity and sustainability.
In all these fields and more, understanding the end behavior of functions provides critical insights and helps make informed predictions and decisions.
Exercise
Example 1
Polynomial Function
Find the end behavior of the function: f(x) = 2x⁴ – 5x² + 1
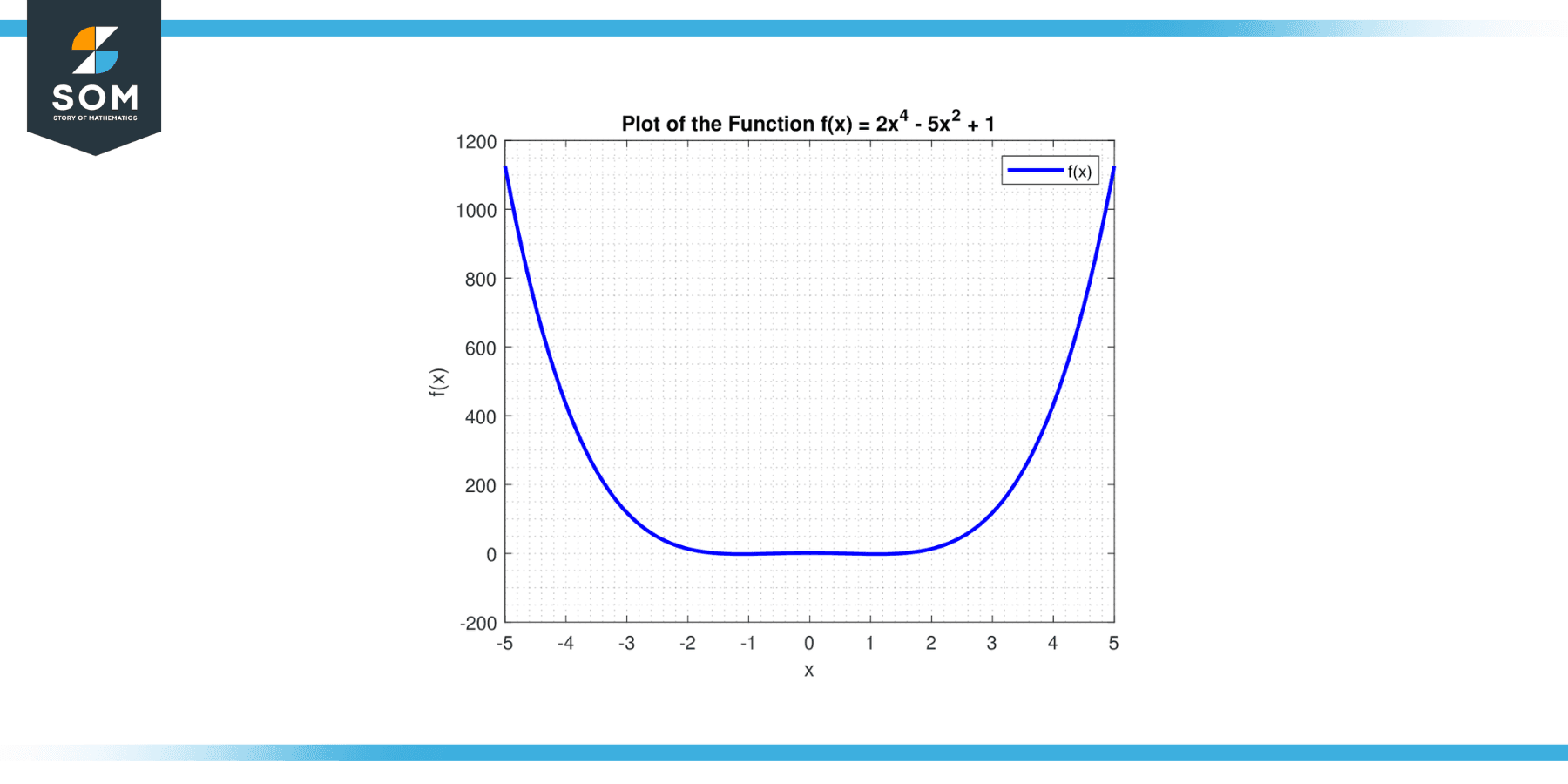
Figure-4.
Solution
The highest degree (4) is even, and the leading coefficient (2) is positive. Therefore, as x approaches positive or negative infinity, f(x) also approaches positive infinity. In terms of notation, we write this as:
lim (x->+∞) f(x) = +∞
lim (x->-∞) f(x) = +∞
Example 2
Polynomial Function
Find the end behavior of the function: f(x) = -3x^5 + 4x³ – x + 2
Solution
The highest degree (5) is odd, and the leading coefficient (-3) is negative. Therefore, as x approaches positive infinity, f(x) approaches negative infinity, and as x approaches negative infinity, f(x) approaches positive infinity. We write this as:
lim (x->+∞) f(x) = -∞
lim (x->-∞) f(x) = +∞
Example 3
Rational Function
Find the end behavior of the function: f(x) = (3x² + 2) / (x – 1)
Here, the degree of the numerator (2) is higher than that of the denominator (1). Thus, as x approaches positive or negative infinity, f(x) also approaches positive or negative infinity, depending on the sign of x. We write this as:
lim (x->+∞) f(x) = +∞
lim (x->-∞) f(x) = -∞
Example 4
Rational Function
Find the end behavior of the function: f(x) = (2x + 1) / (x² – 4)
Solution
Here, the degree of the numerator (1) is less than that of the denominator (2). Therefore, as x approaches positive or negative infinity, f(x) approaches 0. We write this as:
lim (x->+∞) f(x) = 0
lim (x->-∞) f(x) = 0
Example 5
Exponential Function
Find the end behavior of the function: f(x) = 2ᵡ
Solution
As x approaches positive infinity, f(x) approaches positive infinity. And as x approaches negative infinity, f(x) approaches 0. We write this as:
lim (x->+∞) f(x) = +∞
lim (x->-∞) f(x) = 0
Example 6
Cubic Function
Find the end behavior of the function: f(x) = 3x³
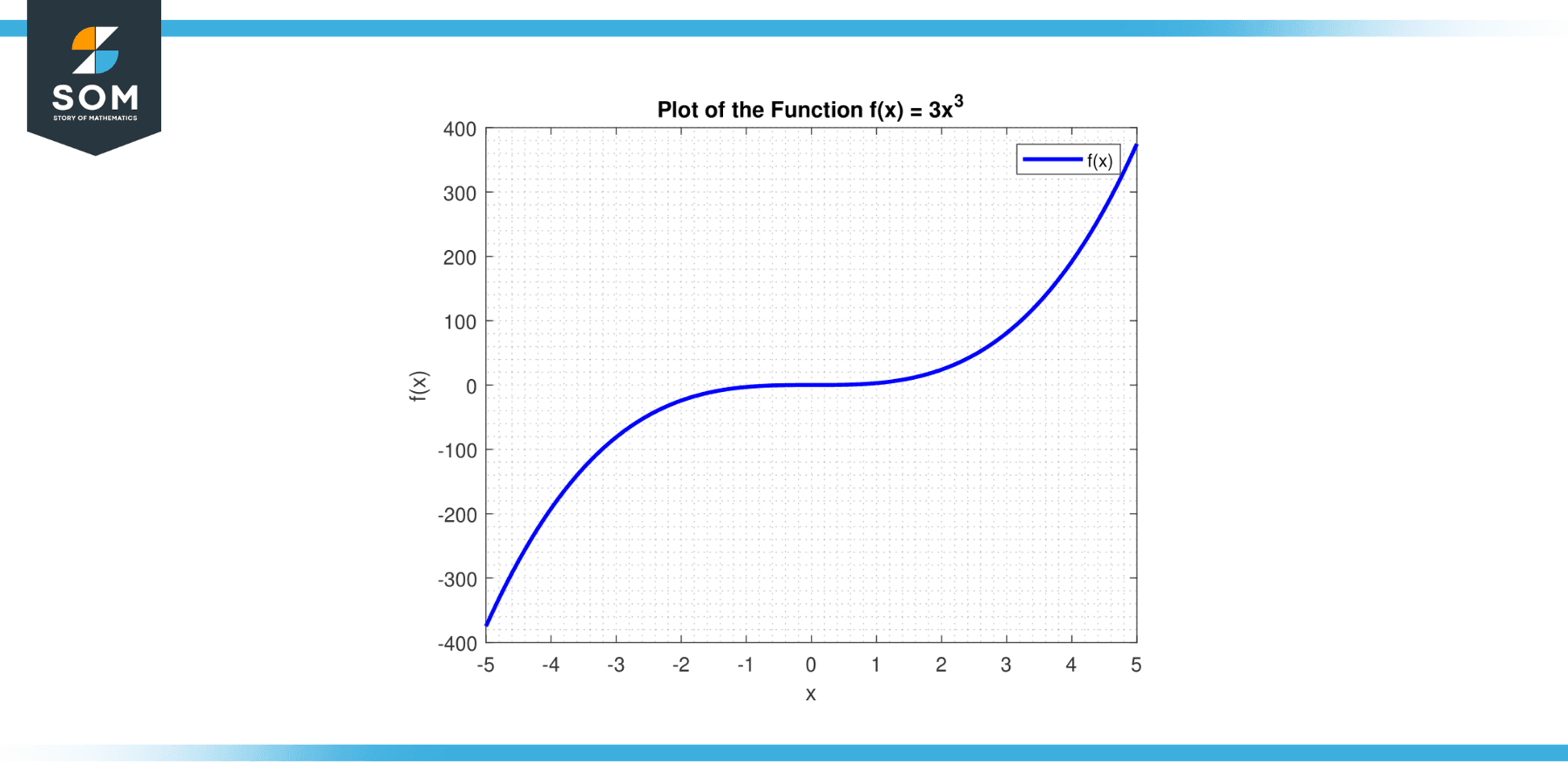
Figure-5.
Solution
The degree is 3, which is odd, and the leading coefficient (3) is positive. Therefore, as x approaches positive infinity, f(x) also approaches positive infinity, and as x approaches negative infinity, f(x) approaches negative infinity. We write this as:
lim (x->+∞) f(x) = +∞
lim (x->-∞) f(x) = -∞
This end behavior is typical for cubic functions with a positive leading coefficient. As x gets large in either the positive or negative direction, the term with the highest power (3) dominates the function, leading to the observed end behavior.
Example 7
Quadratic Function
Find the end behavior of the function: f(x) = -2x² + 3x + 1
The highest degree is 2, which is even, and the leading coefficient (-2) is negative. Therefore, as x approaches positive or negative infinity, f(x) approaches negative infinity. We write this as:
lim (x->+∞) f(x) = -∞
lim (x->-∞) f(x) = -∞
Quadratic functions with a negative leading coefficient always decrease towards negative infinity as x gets large in either the positive or negative direction.
Example 8
Exponential Function
Find the end behavior of the function: f(x) = $\left(\frac{1}{3}\right)^{x}$
Here, the base is less than one. Thus, as x approaches positive infinity, f(x) approaches 0. And as x approaches negative infinity, f(x) approaches positive infinity. We write this as:
lim (x->+∞) f(x) = 0
lim (x->-∞) f(x) = +∞
All images were created with MATLAB.

