The perpendicular bisector theorem states that if a point lies on the perpendicular bisector of a line segment, it will be at an equal distance/equidistant from both endpoints of that line segment.
What Is Perpendicular Bisector Theorem?
The perpendicular bisector theorem is a theorem stating that if we take any point on the perpendicular bisector of a line segment, then that point will be equidistant from both the endpoints of the line segment. This is shown in the figure below.
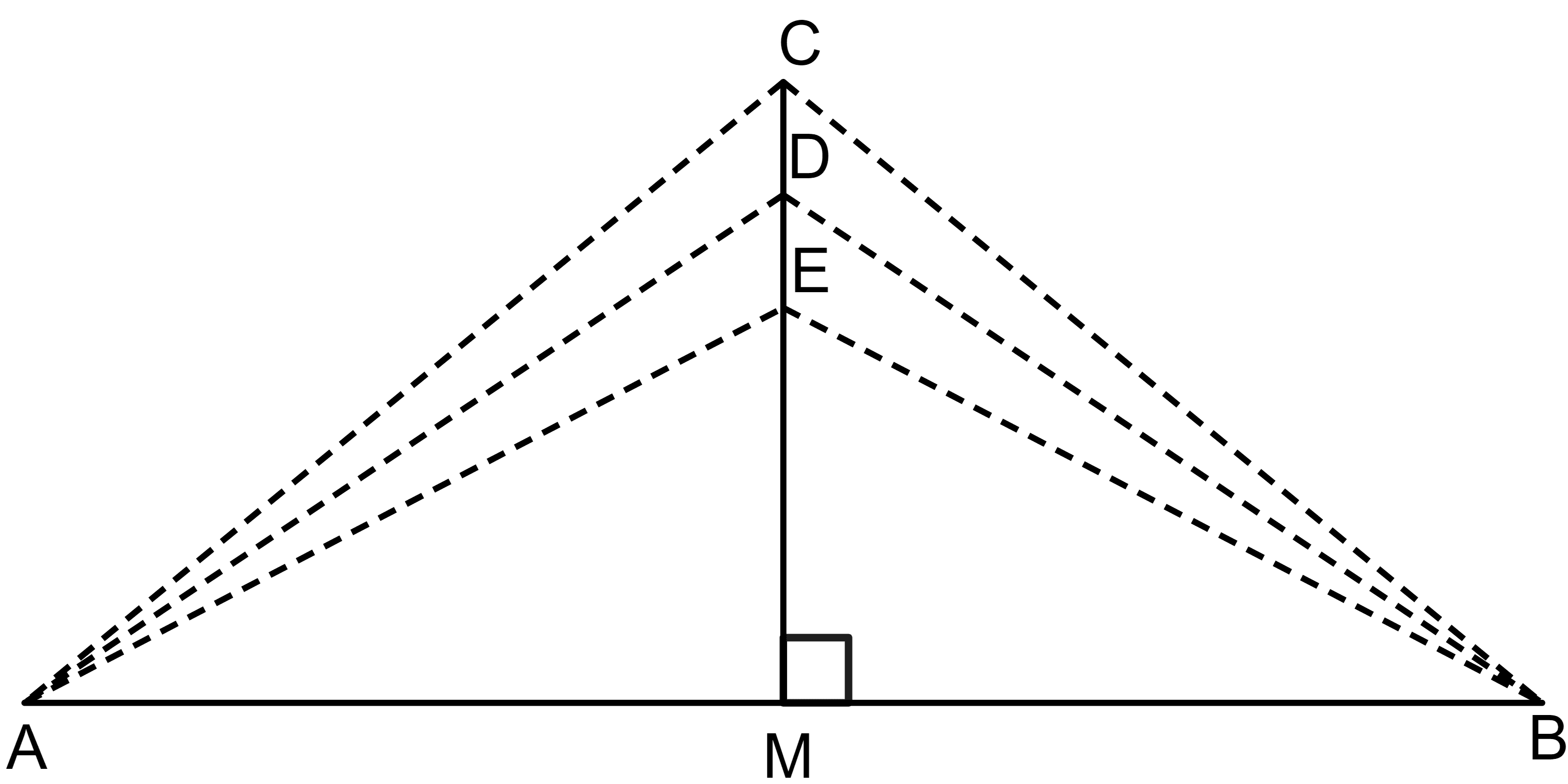
According to perpendicular bisector theorem:
$CA = CB$
$DA = DB$
$EA = EB$
Perpendicular Bisector
Consider two line segments, “$AB$” and “$CD$”. If the two segments cut each other in a manner that an angle of $90^{o}$ is formed, then they are perpendicular to each other.
If the line segment “$AB$” cuts the line segment “$CD$” such that it divides the line segment “$CD$” into two equal parts, then we will say that both these lines bisect each other. So if the line segment “$AB$” bisects line segment “$CD$” at a $90^{o}$ angle, it will give us the perpendicular bisector.
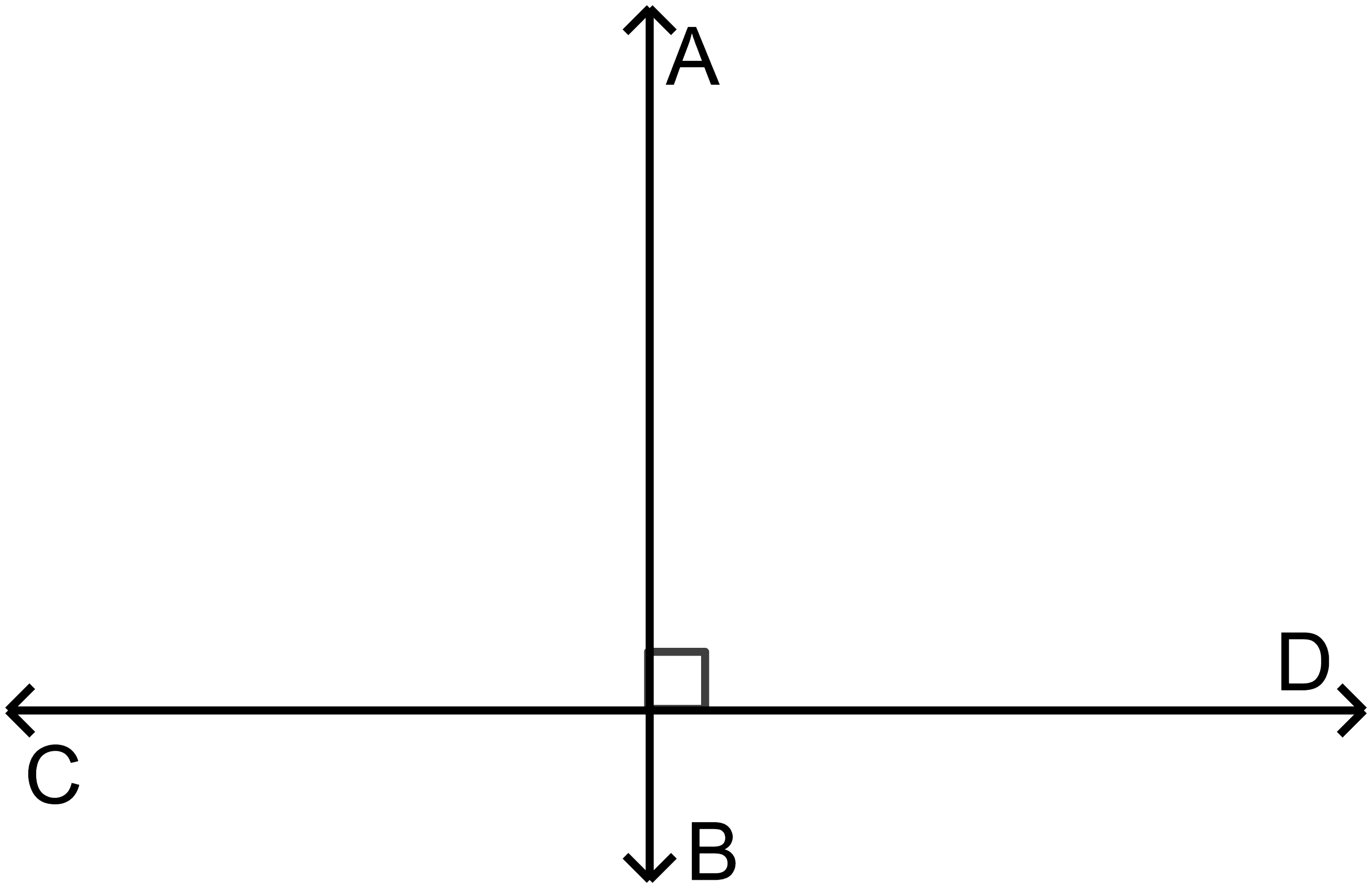
Note: In the above example, we can take a line or a ray instead of line segment “$AB$” as long as it is still bisecting the line segment “$CD$” at a $90^{o}$ angle. But we cannot take a line/ray instead of the line segment “$CD$” as a line/ray has an infinite length and cannot be cut in two equal halves.
How To Use Perpendicular Bisector Theorem
We can use the perpendicular bisector theorem to determine the missing lengths of the sides of a triangle if sufficient data regarding the triangle is already given. Perpendicular bisector theorem can also be used along with other theorems to solve for lengths of a triangle.
Consider an example of a weather monitoring tower that is erected at a $90^{o}$ angle in the center of a piece of land. The land is $800$m in length while the tower’s height is $250$ meters, and we want to attach two guy-wires from the top of the tower to the end of the ground. Perpendicular bisector theorem and Pythagoras theorem will help us determine the length of the guy-wires.
The tower is like a perpendicular bisector for the land, so it bisects the land into two equal parts of $400$ meters. The height of the tower is given as 250 meter, so let us calculate the length of one guy-wire using Pythagoras theorem.
$c^{2}= 400^{2} + 250^{2}$
$c^{2} = 160,000 + 62,500$
$c^{2} = 222,500$
$c = \sqrt{222,500} = 472$ meter approx.
We know that any point on the perpendicular bisector is at equal distance from both ends, so the length of the other guy wire is also $472$ meter approx.
We used the perpendicular bisector theorem to calculate the missing length of the triangle sides in the above example. The conditions for utilization of perpendicular bisector are simple and can be stated as:
- The line, ray or line segment must bisect the other line segment at a $90^{o}$ angle.
- We must have sufficient data regarding the problem to solve for the remaining sides of the triangle.
Proof of Perpendicular Bisector Theorem
It is a pretty straightforward proof. Let us draw a bisector on the line segment XY. The spot where the bisector touches the line segment is M, and we have to prove that the lines drawn from point C on the bisector to the endpoints X and Y are congruent or equal to each other.
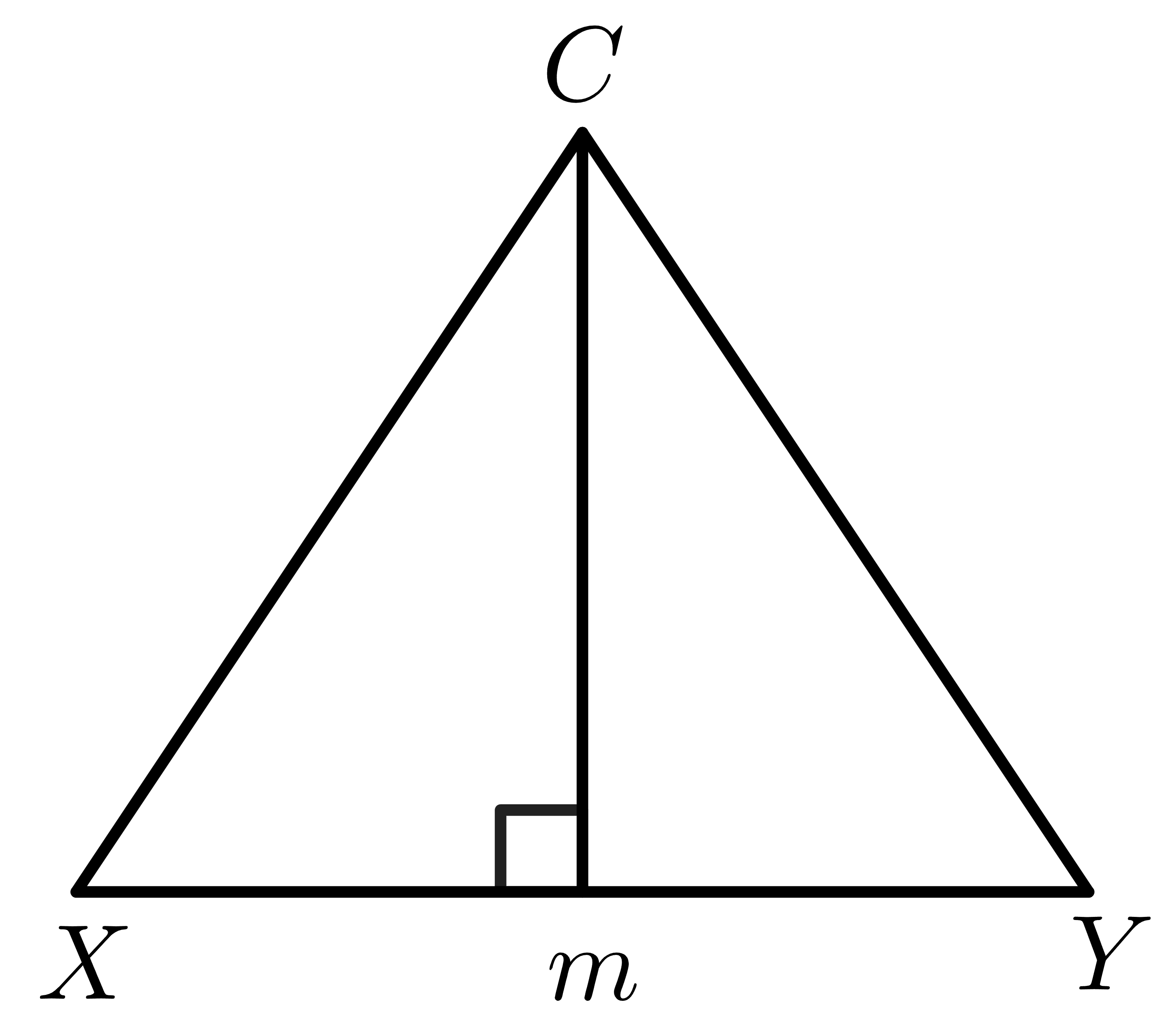
If we assume that the line CM is a perpendicular bisector of the line segment XY, then this means it bisects the XY at a $90^{0}$ angle and that the point M is the middle point of the line segment XY. Then by the definition of a perpendicular bisector, we have divided the line segment into two equal parts, so XM and MY are congruent.
$XM = MY$
If we draw two lines from the point $C$ to the endpoints of line segment $X$ and $Y$, we will get two right-angle triangles $XMC$ and $YMC$. We have already concluded that the XM and MY are congruent. Similarly, the bisector length for both triangles will also be the same.
$CM = CM$ ( for both triangles)
We have established that two sides and one angle (the $90^{0}$ one) of the two triangles $XMC$ and $YMC$ are equal. So by SAS congruent criteria, we know that angles $XMC$ and $YMC$ are congruent.
This provides us with the conclusion that the sides $CX$ and $CY$ are congruent.
Proof of Converse Perpendicular Bisector Theorem
The converse perpendicular bisector theorem reverses the hypothesis of the original theorem. It states that if point M is equidistant from both endpoints of the line segment $XY$, it is a perpendicular bisector of that line segment.
Using the same picture above, if $CX = CY$,
Then we have to prove that $XM = YM$.
Draw a perpendicular line from point $C$ such that it cuts the line segment at point M.
Now compare $\triangle XMC$ and $\triangle YMC$:
$CX = CY$
$CM = CM$ ( for both traingles)
$\angle XMC = \angle YMC = 90^{o}$
So $\triangle XMC \cong \triangle YMC$ by SAS congruent criteria. Hence, $XM = YM$ is proved.
Applications of Perpendicular Bisector Theorem
1. It is extensively used in the construction of bridges.
2. It is also used for the erection of towers and installing guy-wires around it.
3. It is used in making tables of different sizes and lengths.
Example 1:
For the figure given below, calculate the value of “$x$”.
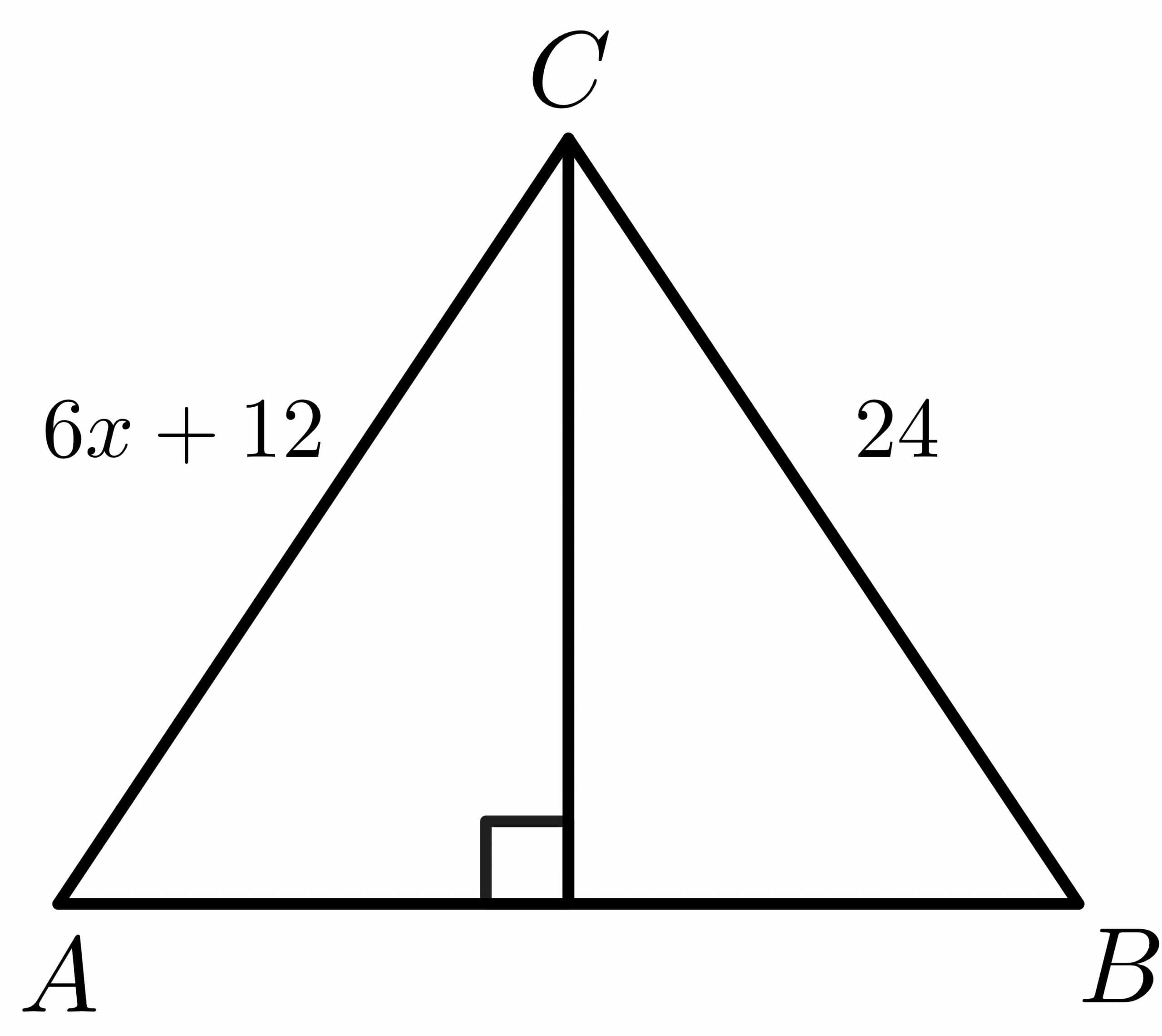
Solution:
We know that for a perpendicular bisector, the side $AC = BC$.
$6x\hspace{1mm} +\hspace{1mm}12 = 24$
$6x = 24\hspace{1mm} -\hspace{1mm}12$
$6x = 12$
$x = \dfrac{12}{6} = 2$
Example 2:
Solve the unknown values of the triangle by using properties of the perpendicular bisector theorem.
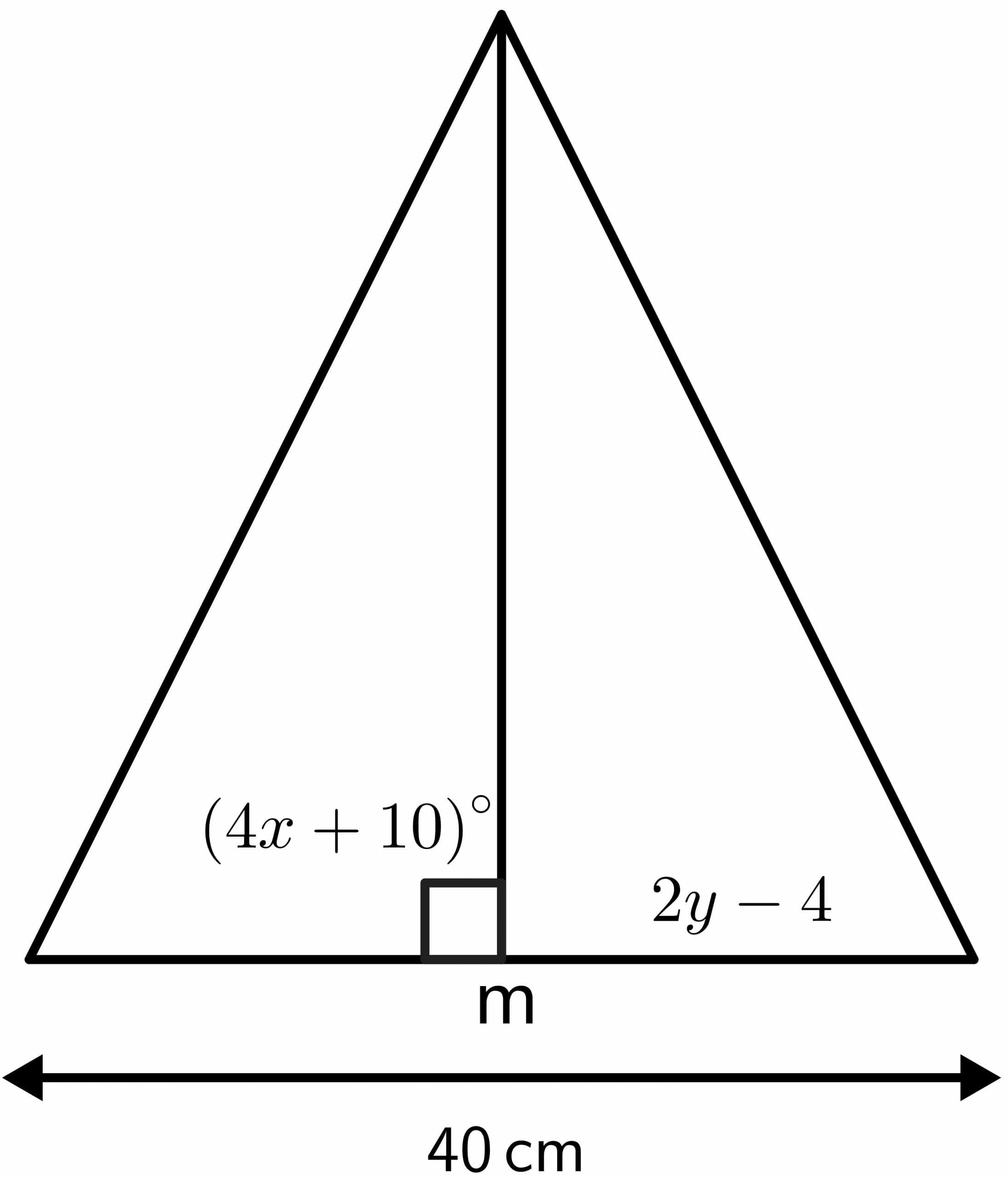
Solution:
We know that the angle where perpendicular bisector bisects is equal to $90^{o}$.
$4x\hspace{1mm} + \hspace{1mm}10 = 90$
$4x = 80$
$x = 40^{o}$
The perpendicular bisector will divide the given length of $40 cm$ into two equal parts of $20 cm$ each. Hence, $2y – 4$ will be equal to $20 cm$.
$2y – 4 = 20$
$2y = 24$
$y = 12 cm$
Example 3:
Using the properties of the perpendicular bisector theorem, calculate the value of “x” for the figure given below.
Solution:
From the properties of the perpendicular bisector theorem, we know that the side $AB = BC$.
$6x\hspace{1mm} +\hspace{1mm}4 = 8x\hspace{1mm} -\hspace{1mm}2$
$8x\hspace{1mm} – \hspace{1mm}6x = 4\hspace{1mm}+\hspace{1mm}2$
$2x = 6$
$x = \dfrac{6}{2} = 3$
Example 4:
Calculate the lengths of the unknown sides of the triangle by using the perpendicular bisector theorem.
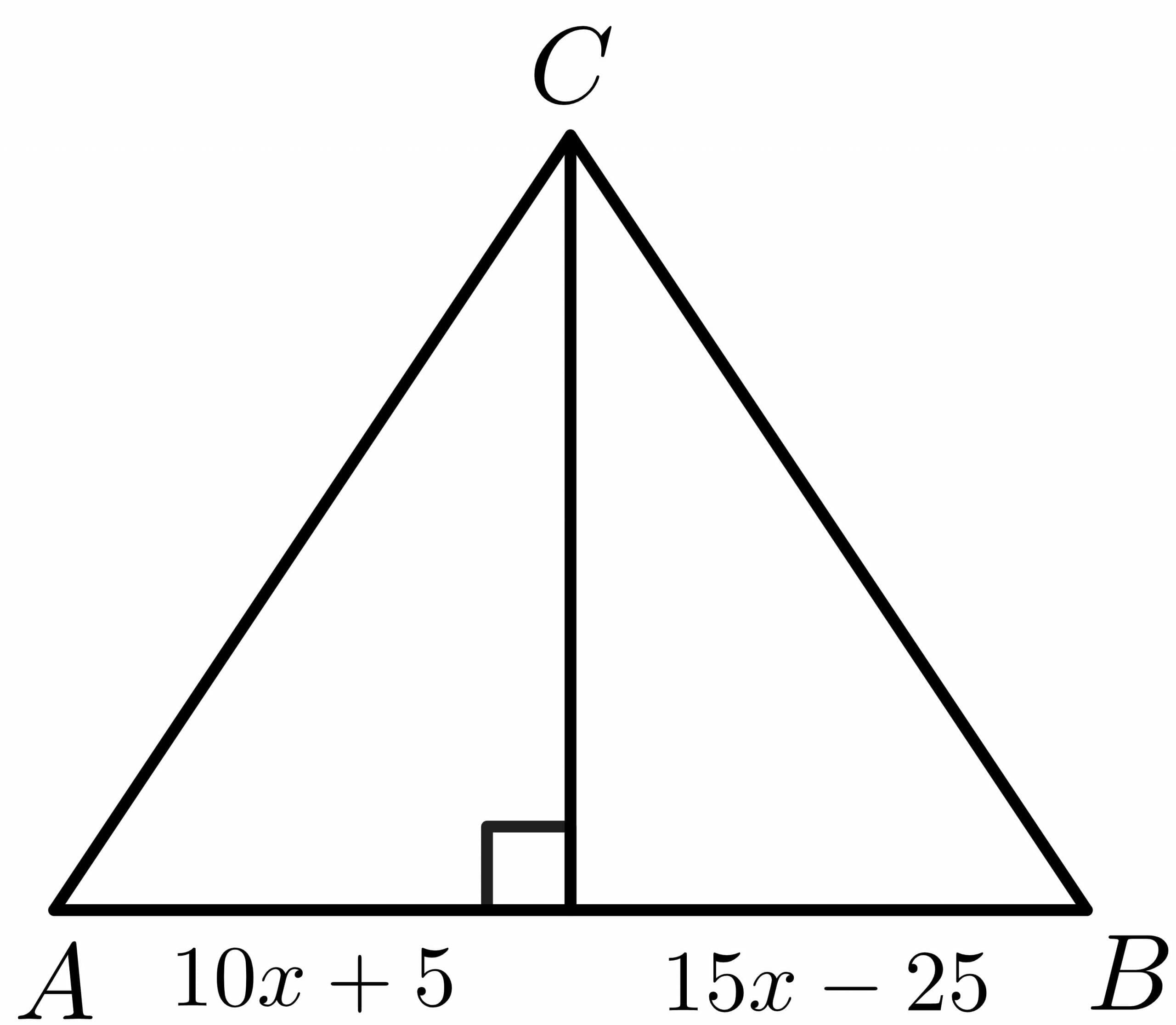
Solution:
From the properties of the perpendicular bisector theorem, we know that the side $AD = BD$.
$10x\hspace{1mm} +\hspace{1mm}5 = 15x -25$
$15x – 10x = 5\hspace{1mm}+\hspace{1mm}25$
$5x = 30$
$x = \dfrac{30}{5} = 6$
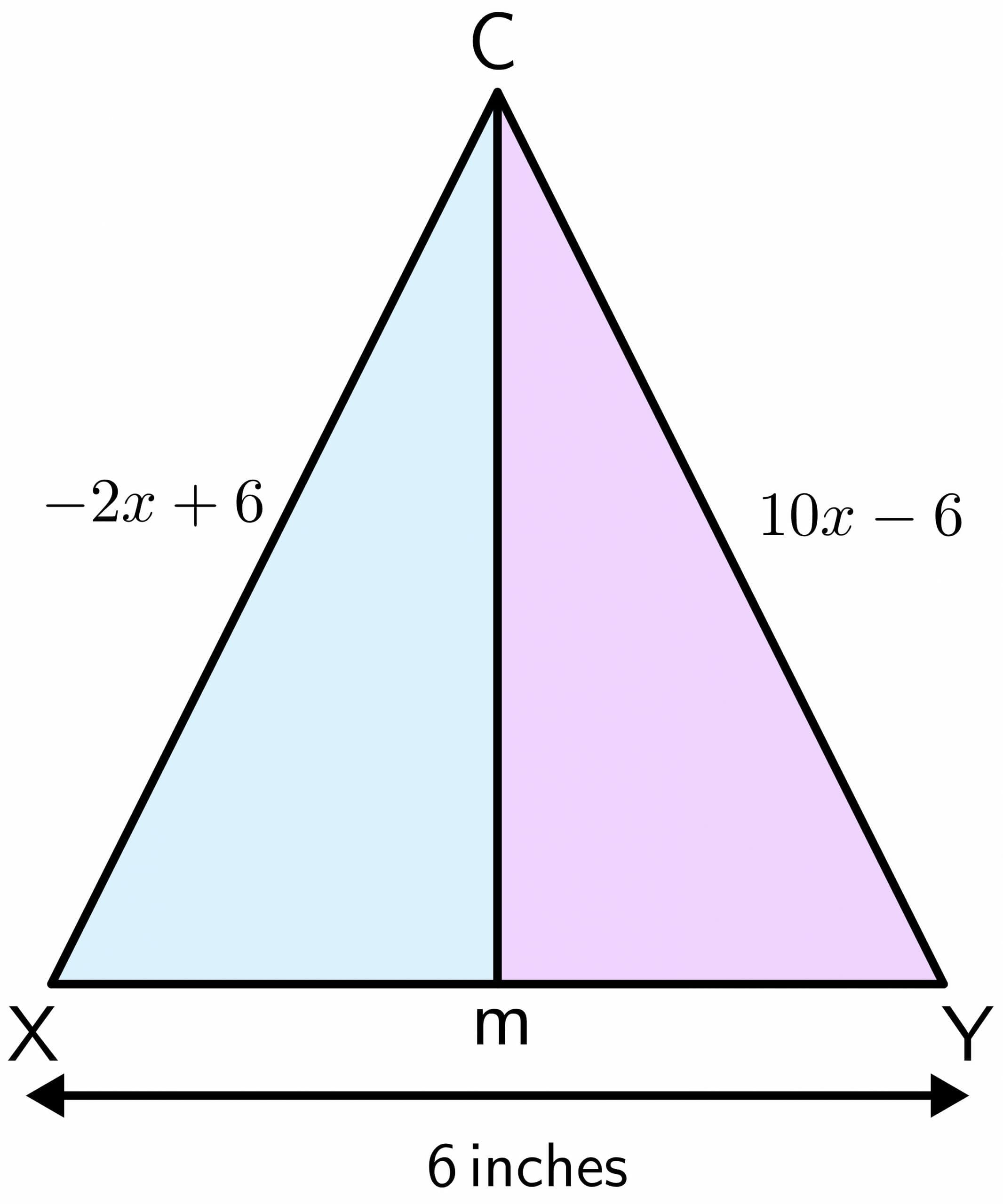
Example 5:
Mason is standing in a playground. The playground is used for playing football, and it has a pair of goalposts. The distance between the two poles is $6$ inches. Suppose Mason was standing at point C, and he moves forward in a straight line and ends up at point M between the two poles. If the distance of one pole to point C is $-2x\hspace{1mm} +\hspace{1mm}6$ and the distance of the other pole to point C is $10x\hspace{1mm} –\hspace{1mm} 6$ inches, then calculate the distance covered by Mason from point C to M.
Solution:
Let us draw the figure for the given problem. When Mason moves in a straight line from point C to M, it forms a perpendicular bisector on the two poles. Assume one pole is X and the other is Y.
$-2x +6 = 10x – 6$
$10x + 2x = 6+6$
$12x = 12$
$x = \dfrac{12}{12} = 1$
Putting the value of “$x$” in both equations:
$-2 (1) \hspace{1mm}+\hspace{1mm} 6 = -2 \hspace{1mm}+ \hspace{1mm}6 = 4$ inches
$10(1) \hspace{1mm}–\hspace{1mm} 6 = 10\hspace{1mm} – \hspace{1mm}6 = 4$ inches
As M is the mid point of XY and it divides XY equally in half, so the length for XM and YM is equal to $3$ inches each.
Applying Pythagoras theorem to calculate the distance covered by Mason from point C to M:
$XC^{2} = XM^{2}\hspace{1mm} +\hspace{1mm} CM^{2}$
$CM = \sqrt{XC^{2}\hspace{1mm}- \hspace{1mm}XM^{2}}$
$CM = \sqrt{4^{2}\hspace{1mm}-\hspace{1mm} 20^{2}}$
$CM = \sqrt{16 \hspace{1mm}-\hspace{1mm} 9}$
$CM = \sqrt {7} = 2.65$ inches approx.
Practice Questions
- Using the properties of perpendicular bisector theorem, calculate the value of “x” for the figure given below.
- Prove that the vertex between the two equal sides in an isosceles triangle lies on the perpendicular bisector of the base.
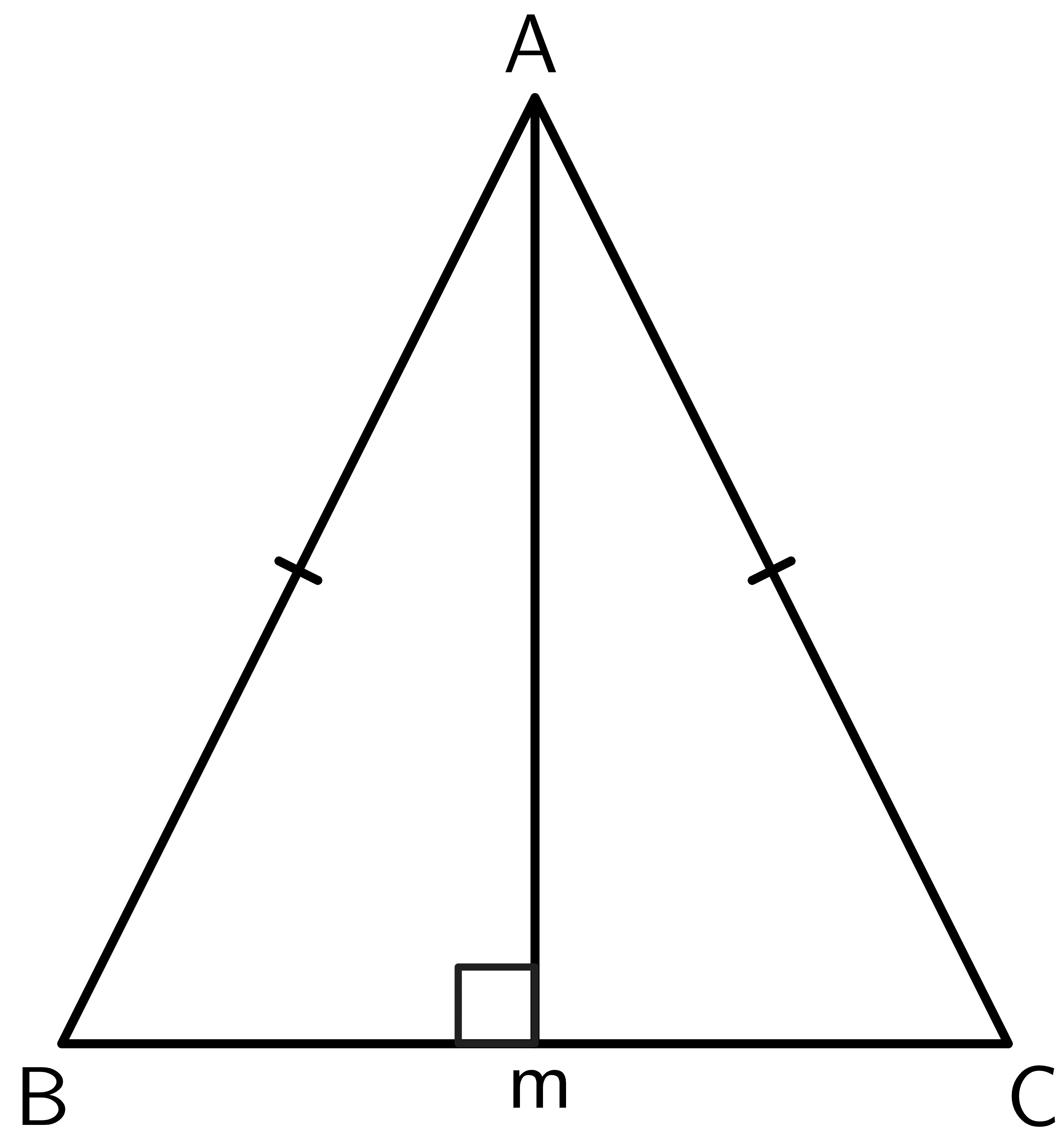
Answer Key
1.
From the properties of perpendicular bisector theorem, we know that the side $AC = BC$.
$12x \hspace{1mm}+\hspace{1mm} 4 = 8x\hspace{1mm} +\hspace{1mm}12$
$12x\hspace{1mm} –\hspace{1mm} 8x = 12\hspace{1mm} –\hspace{1mm} 4$
$4x = 8$
$x = \dfrac{8}{4} = 2$
2.
Let us draw a perpendicular from the vertex $A$ to point $M$ at the line segment $BC$. As the triangle is an isosceles, $AB$ and $AC$ are equal. So the point $A$ is equidistant from the endpoints of $BC$. By converse perpendicular bisector theorem,
$BM = CM$
Hence, the vertex lies on the perpendicular bisector of base $BC$.