JUMP TO TOPIC
Mastering triangle reflection tests our understanding of transformations and reflections that occur on a rectangular coordinate plane. The triangle is a polygon made up of three points, so we’re observing the reflections of these three points when learning how to reflect triangles on the coordinate system.
Triangle reflection extends our knowledge of reflecting a point on a coordinate system to reflecting three points forming a triangle.
In this article, we’ll show you the process of reflecting a triangle on a coordinate plane. By learning how to reflect these figures over a given line of reflection, we’ll apply our understanding of reflecting points over a coordinate plane. By the end of our discussion, we want you to feel confident when working on reflections of triangles.
What Is a Triangle Reflection?
Triangle reflection is the figure obtained when a triangle is flipped on a coordinate system based on a line of reflection. When studying and working on the reflection of polygons like the triangle, it’s important to know the following terms:
- Pre-image: The original image (for this discussion, the triangle) that we’re reflecting over a line.
- Image: The reflected triangle and final version after reflecting the triangle over.
We normally label the image using the pre-image’s points but this time, we add a prime symbol to each of these points’ labels. Let’s take a look at the two triangles plotted on the same $xy$-plane.
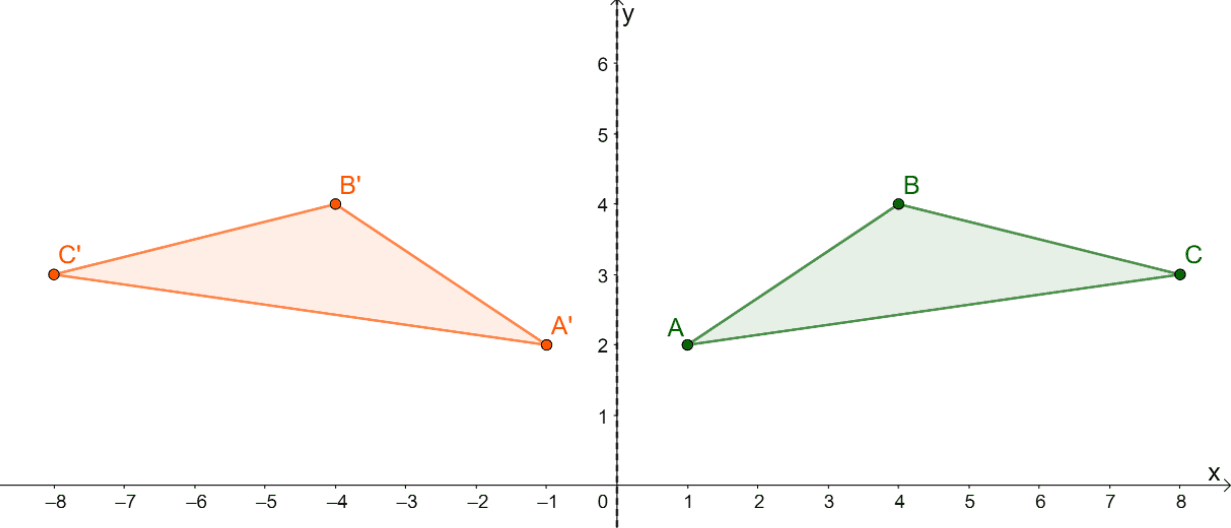
Suppose that the triangle, $ABC$, is the triangle we want to reflect over the $y$-axis or the line, $x=0$. If $ABC$ is the pre-image, then the triangle, $A^{\prime}B^{\prime}C^{\prime}$ is the resulting image after reflecting the triangle.
When working with triangle reflections, the resulting image will retain the shape of the triangle. This means that the lengths and angle measures of these two triangles will be equal.
In triangle reflection, however, the triangle from the pre-image and the image may have different positions. Why don’t we take a look at the points of the triangle, $\Delta ABC$, after being reflected over the $y$-axis?
Pre-Image | Image |
\begin{aligned} A= (1, 2)\end{aligned} | \begin{aligned} A^{\prime}= (-1, 2)\end{aligned} |
\begin{aligned} B= (4, 4)\end{aligned} | \begin{aligned} B^{\prime}= (-4, 4)\end{aligned} |
\begin{aligned} C= (8, 3)\end{aligned} | \begin{aligned} C^{\prime}= (-8, 2)\end{aligned} |
We’ve learned that when reflecting points over the $y$-axis, the $x$-coordinate’s sign changes. We extend this concept when reflecting triangles, so the reflection of triangles will depend on the line of reflection as well.
These are the common lines of reflection that you’ll encounter for triangle reflection:
- The $x$-axis with an equation of $y= 0$
- The $y$-axis with an equation of $x= 0$
- The diagonal line with an equation of $y =x$
- The diagonal line with an equation of $y = -x$
In the next section, we’ll show you how the triangle’s points are affected when the pre-image of the triangle is reflected over these lines. We’ll also show you different examples of reflecting a triangle to help you understand the process better!
How To Reflect a Triangle?
Reflect a triangle by 1) reflecting the three points that form each triangle over the line of reflection and 2) applying the algebraic properties of reflections on each coordinate.
In triangle reflection, the point of the pre-image will have the same distance as that of the image’s point with respect to the line of reflection. This is one way to do this properly.
Now let’s take a look at the triangle $\Delta ABC$. If we want to reflect this over the $x$-axis, the distance of the new triangle’s image must have the same distances as that of points $A$, $B$ and $C$ from the $x$-axis.
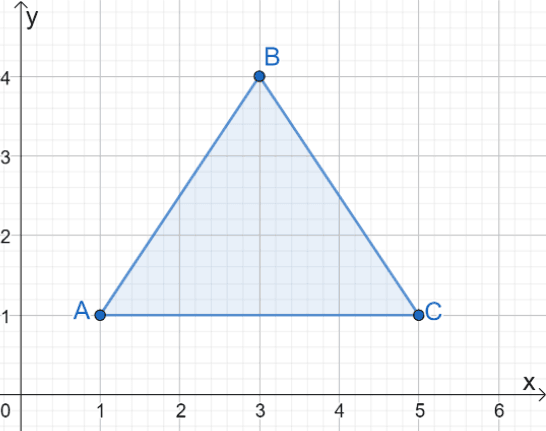
To do so, use the $x$-axis or the line presented by $y = 0$, and measure the distances of $A$, $B$, and $C$.
- The points $A$ and $C$ are one unit away from the $x$-axis.
- The point $B$ is 4 units away from the $x$-axis.
- Reflect the $x$-axis by plotting the image’s points right below the $x$-axis.
Once the reflection’s image is plotted, construct the triangle to show the reflected triangle. Take a look at the image shown below to see how the $\Delta ABC$ is reflected over the $x$-axis.
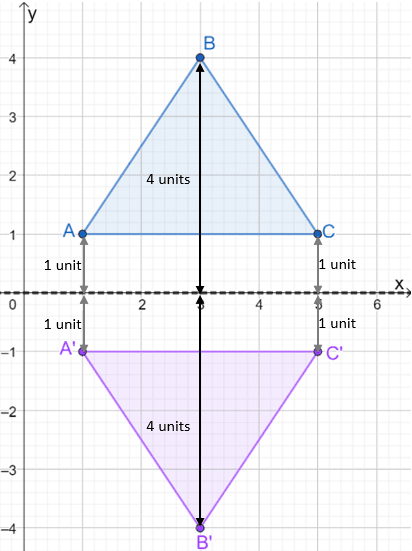
We use the same process when reflecting triangles over different lines of reflections. For now, let’s also take a look at how the coordinates change from the pre-image to the image.
Pre-Image | Image |
\begin{aligned} A= (1, 1)\end{aligned} | \begin{aligned} A^{\prime}= (1, -1)\end{aligned} |
\begin{aligned} B= (4, 4)\end{aligned} | \begin{aligned} B^{\prime}= (4, -4)\end{aligned} |
\begin{aligned} C= (5, 1)\end{aligned} | \begin{aligned} C^{\prime}= (5, -1)\end{aligned} |
This confirms that when we reflect a triangle over the $x$-axis, we’re simply reflecting the three coordinates by changing the $y$-coordinate’s sign. This means that we can apply the rules of a coordinate reflection to triangle reflection. With this in mind, let’s go ahead and move on to another way of reflecting triangles – by focusing on the vertices’ coordinates.
Here’s a summary of the rules to remember when reflecting the triangles’ coordinates over these four common lines of reflection.
Reflection | Coordinate of the Image |
Reflection over the $x$-axis | \begin{aligned} (x, y) \rightarrow (x, -y)\end{aligned} |
Reflection over the $y$-axis | \begin{aligned} (x, y) \rightarrow (-x, y)\end{aligned} |
Reflection over the line, $y = x$ | \begin{aligned} (x, y) \rightarrow (y, x)\end{aligned} |
Reflection over the line, $y = -x$ | \begin{aligned} (x, y) \rightarrow (-y, -x)\end{aligned} |
Reflection over the origin | \begin{aligned} (x, y) \rightarrow (-x, -y)\end{aligned} |
The best way to master this topic by heart is through practice. We’ll show you examples and practice questions for you to work on. When you’re ready, head over to the section below!
Example 1
What would the reflection of $\Delta MNO$ look like when reflected over the origin?
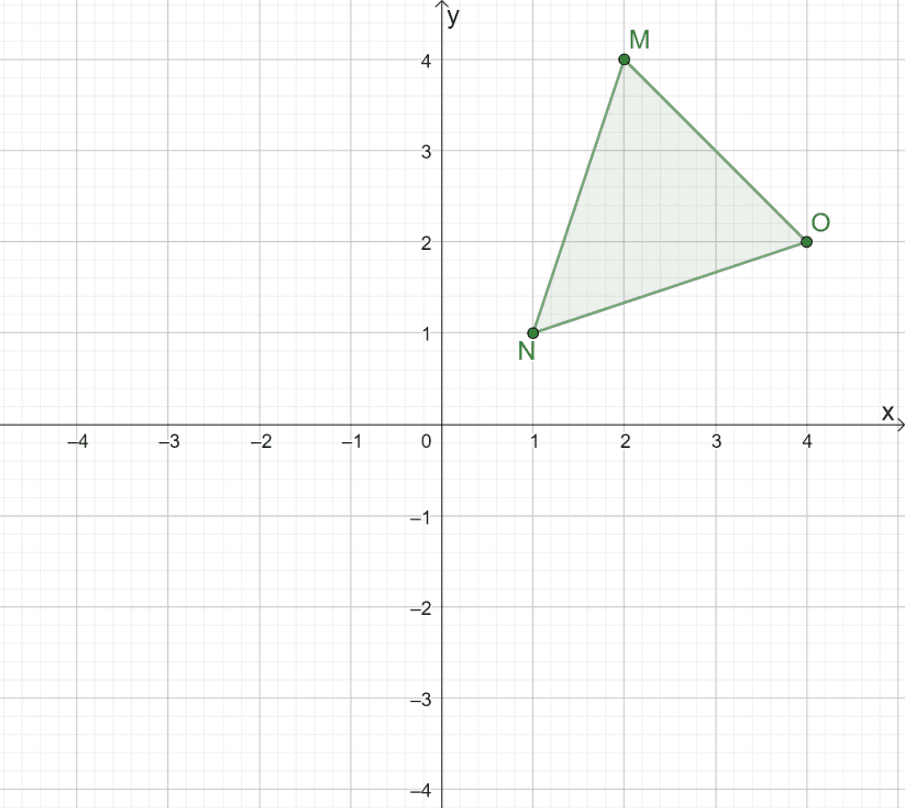
Solution
To graphically reflect the triangle $\Delta MNO$, first construct a line to guide us in reflecting the triangle over the origin. When reflecting a triangle over the origin, use a line where $(0, 0)$ is the midpoint between $M$ and $M^{\prime}$.
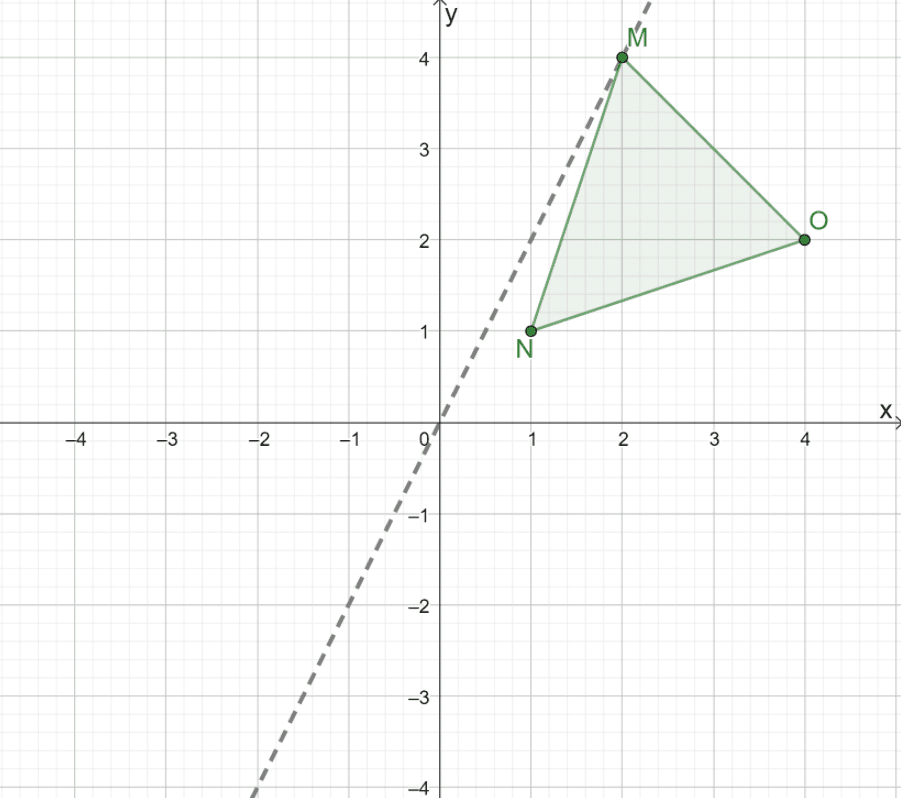
Now, observe the perpendicular distance of the three vertices from this line.
- The line passes through point $M$, so it will be passing $M^{\prime}$ through as well.
- The point, $N$, is roughly $0.5$ unit from the right of the line. This means that point $N^{\prime}$ is approximately $0.5$ unit from the left.
- Similarly, since $O$ is $4$ units away from the right of the line, $O^{\prime}$ is $4$ units to the left of the line.
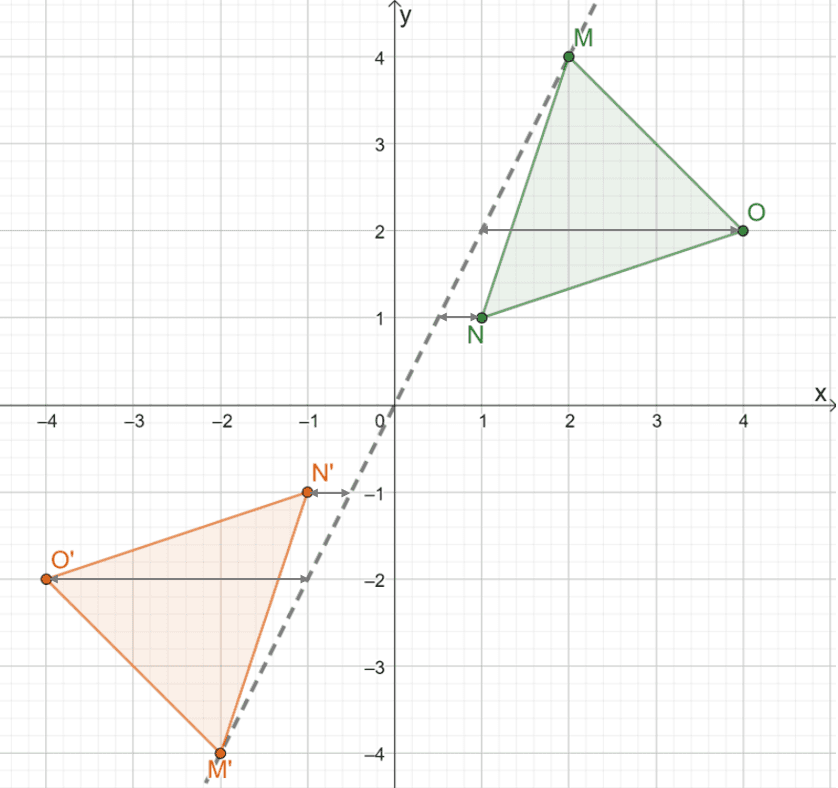
Hence, the result of reflecting $\Delta MNO$ over the origin is the image $\Delta M^{\prime}N^{\prime} O^{\prime}$. If we apply the second method, we can determine the coordinates of the triangle’s image by multiplying the $x$ and $y$-coordinates of each point by $-1$.
Pre-Image | Image |
\begin{aligned} A= (2, 4)\end{aligned} | \begin{aligned} A^{\prime}= (-2, -4)\end{aligned} |
\begin{aligned} B= (1, 1)\end{aligned} | \begin{aligned} B^{\prime}= (-1, -1)\end{aligned} |
\begin{aligned} C= (4, 2)\end{aligned} | \begin{aligned} C^{\prime}= (-4, -2)\end{aligned} |
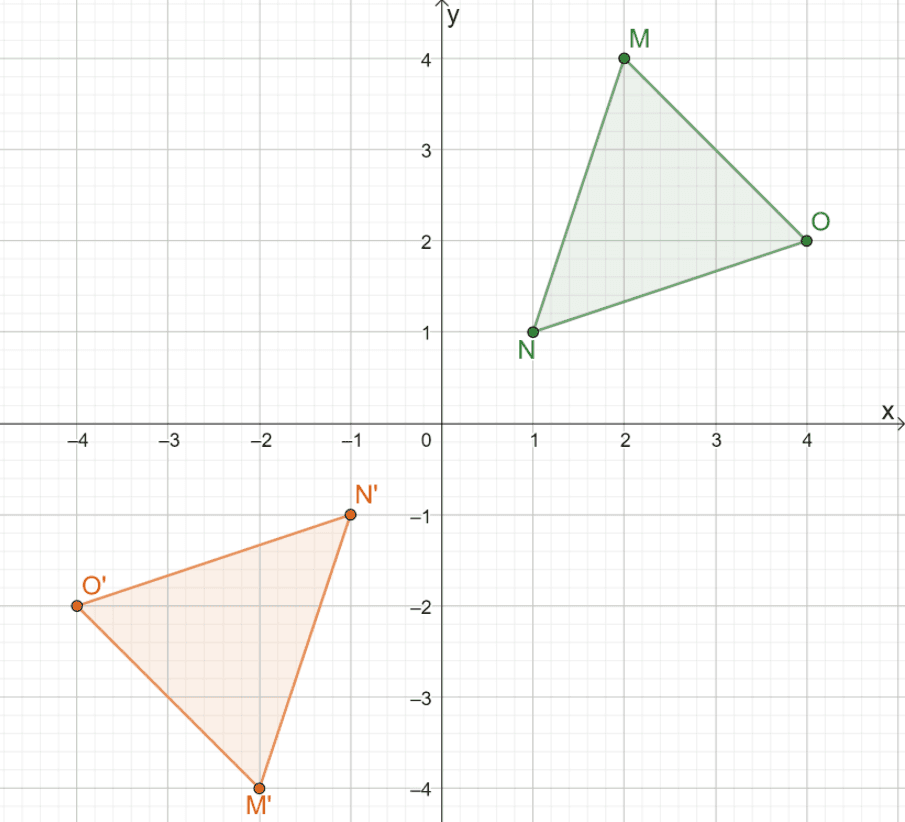
This shows that whichever method we use, the result will remain the same. Using the second approach is more efficient for common lines of reflection.
Knowing how to reflect triangles geometrically, however, allow us to work with a wide range of lines of reflection. This means with the two methods in our toolkit, we’ll feel even more confident to work with lines of reflections – both familiar and new.
Practice Question
1. What are the coordinates of the resulting image when $\Delta ABC$ is reflected over the $y$-axis?
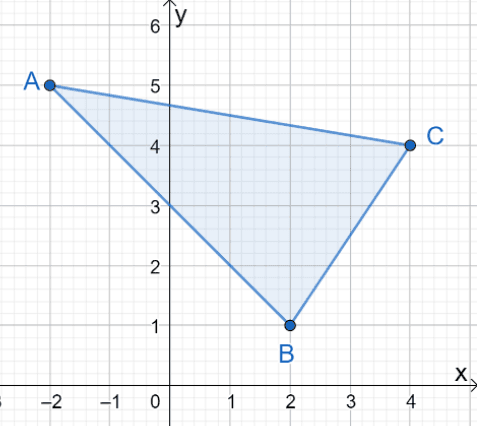
A. $\Delta A^{\prime}B^{\prime}C^{\prime} = \{(-2, -5), (2, -1), (4, -4)\}$
B. $\Delta A^{\prime}B^{\prime}C^{\prime} = \{(2, 5), (-2, 1), (-4, 4)\}$
C. $\Delta A^{\prime}B^{\prime}C^{\prime} = \{(-2, 5), (-2, 1), (-4, 4)\}$
D. $\Delta A^{\prime}B^{\prime}C^{\prime} = \{(2, 5), (2, 1), (4, 4)\}$
2. What are the coordinates of the resulting image when $\Delta ABC$ is reflected over the $x$-axis?
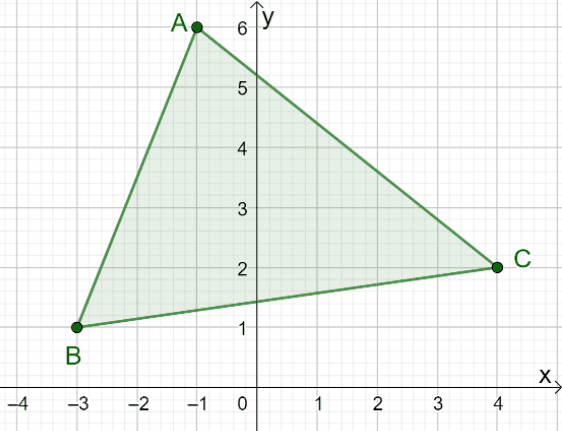
A. $\Delta A^{\prime}B^{\prime}C^{\prime} = \{(-1, -6), (-3, -1), (4, -2)\}$
B. $\Delta A^{\prime}B^{\prime}C^{\prime} = \{(-1, 6), (-3, 1), (4, 2)\}$
C. $\Delta A^{\prime}B^{\prime}C^{\prime} = \{(-1, -6), (3, -1), (-4, -2)\}$
D. $\Delta A^{\prime}B^{\prime}C^{\prime} = \{(1, 6), (3, 1), (4, 2)\}$
3. What are the coordinates of the resulting image when $\Delta ABC$ is reflected over the line $y =x$?
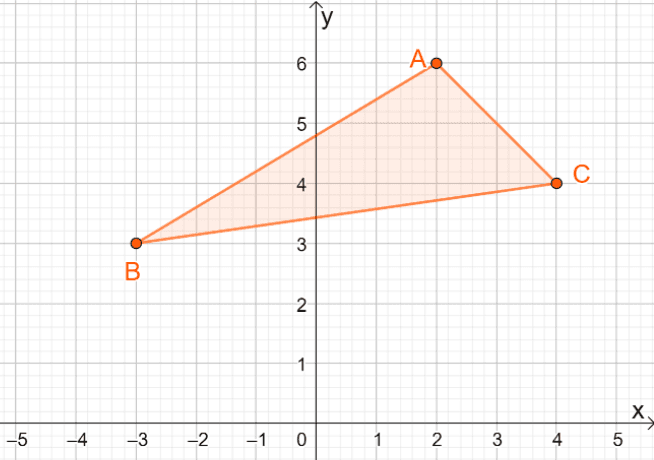
A. $\Delta A^{\prime}B^{\prime}C^{\prime} = \{(-6, 2), (-3, -3), (-4, 4)\}$
B. $\Delta A^{\prime}B^{\prime}C^{\prime} = \{(6, -2), (3, -3), (4, -4)\}$
C. $\Delta A^{\prime}B^{\prime}C^{\prime} = \{(6, 2), (3, -3), (4, 4)\}$
D. $\Delta A^{\prime}B^{\prime}C^{\prime} = \{(-6, 2), (-3, 3), (-4, -4)\}$
4. What are the coordinates of the resulting image when $\Delta ABC$ is reflected over the line $y = – x$?
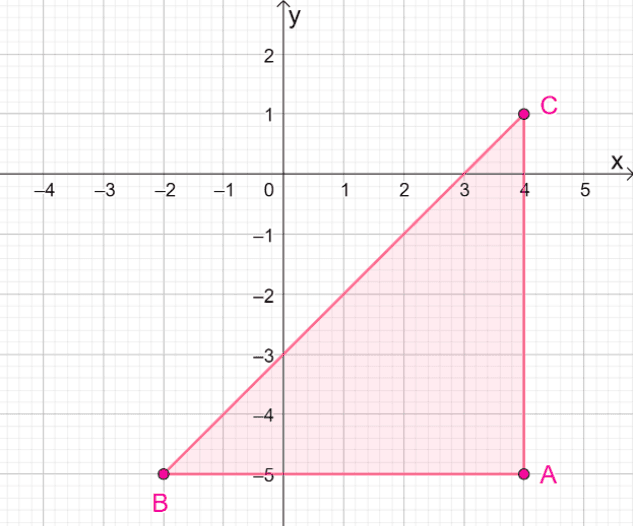
A. $\Delta A^{\prime}B^{\prime}C^{\prime} = \{(-5, -4), (-5, -2), (1, -4)\}$
B. $\Delta A^{\prime}B^{\prime}C^{\prime} = \{(5, -4), (5, -2), (-1, -4)\}$
C. $\Delta A^{\prime}B^{\prime}C^{\prime} = \{(-5, 4), (-5, 2), (1, -4)\}$
D. $\Delta A^{\prime}B^{\prime}C^{\prime} = \{(5, 4), (5, 2), (-1, -4)\}$
Answer Key
1. B
2. A
3. C
4. D
Images/mathematical drawings are created with GeoGebra.
