Hinge Theorem – In-Depth Explanation and Detailed Examples

Hinge theorem states that if two sides of a set of two given triangles are congruent, the triangle with a greater internal angle will have the longer third/remaining side. 

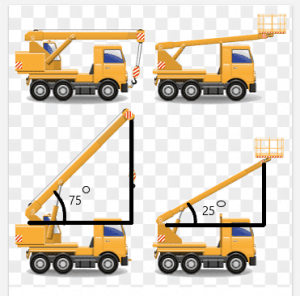
Consider an example of a crane with a beam that can move at different angles. Now, suppose two cranes are equal in length, and the length of their beam is also the same.

The length between the top of the beam and the roof of the crane will depend upon the angle created by the beam.

In this example, the angle made by the beams of the cranes is $75^{o}$ and $25^{o}$, respectively. We can see from the figure that the distance between the top of the beam and the top of the crane is larger for the crane with the angle of $75^{o}$.

This topic will help you understand problems related to triangle inequality and how to solve them by using the Hinge theorem.

What Is Hinge Theorem?

Hinge theorem is a theorem that compares two triangles and states that if two sides of both triangles are equal, then the length/measure of the third side will depend upon the measure of the interior angle. The higher the interior angle, the longer the length of the remaining side. Hinge theorem is also known as the inequality theorem.

So in short, the triangle having a larger interior angle will also have a longer third side.

Consider the example of a $\triangle ABC$ and $\triangle XYZ$. Let $ AB = XY$ and $ AC = XZ$ while the length of the side $BC$ and $YZ$ will depend upon the interior angle. For example, the interior angle of $\triangle ABC$ is $30^{o}$ while the interior angle of $\triangle XYZ$ is $60^{o}$, then both the triangles can be drawn as shown below:

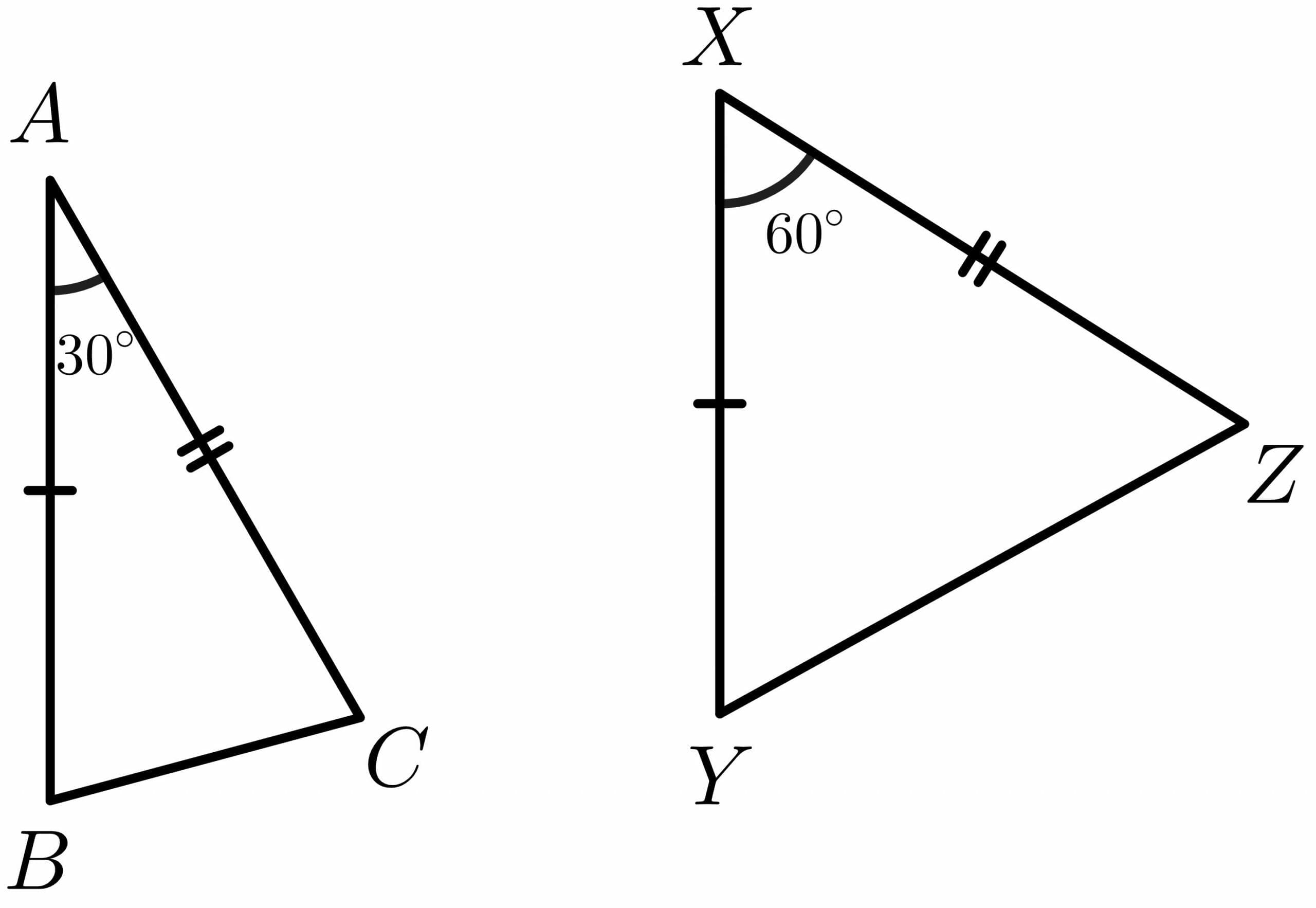
Now take the same triangles $\triangle ABC$ and $\triangle XYZ$ again; the length of all the three sides of the triangles are given, and you are asked to tell which triangle has the greater interior angle. The two sides of the triangles are the same, while the length of the third side varies. Using the hinge theorem, you can easily tell that the triangle with the longer third side will have the larger interior angle. Hinge theorem is also known as the inequality theorem or Hinge theorem inequality.

How To Use Hinge Theorem

The following steps should be kept in mind while using the Hinge theorem to compare triangles.

1. Identify similar sides by looking at the marking or measuring the sides’ length. The sides with the same markings are congruent to each other.
2. The next step is to identify the interior angle of both triangles. If the angles are the same, then S.A.S. postulate states that both triangles are congruent, but if angles differ, the triangle with a larger interior angle will have a longer third side.

Proof of Hinge Theorem

To prove the Hinge theorem, we need to demonstrate that if two sides of one triangle are similar/congruent to another triangle, then the triangle with a larger interior angle will have a larger third side.

Consider this picture of a combination of triangles:

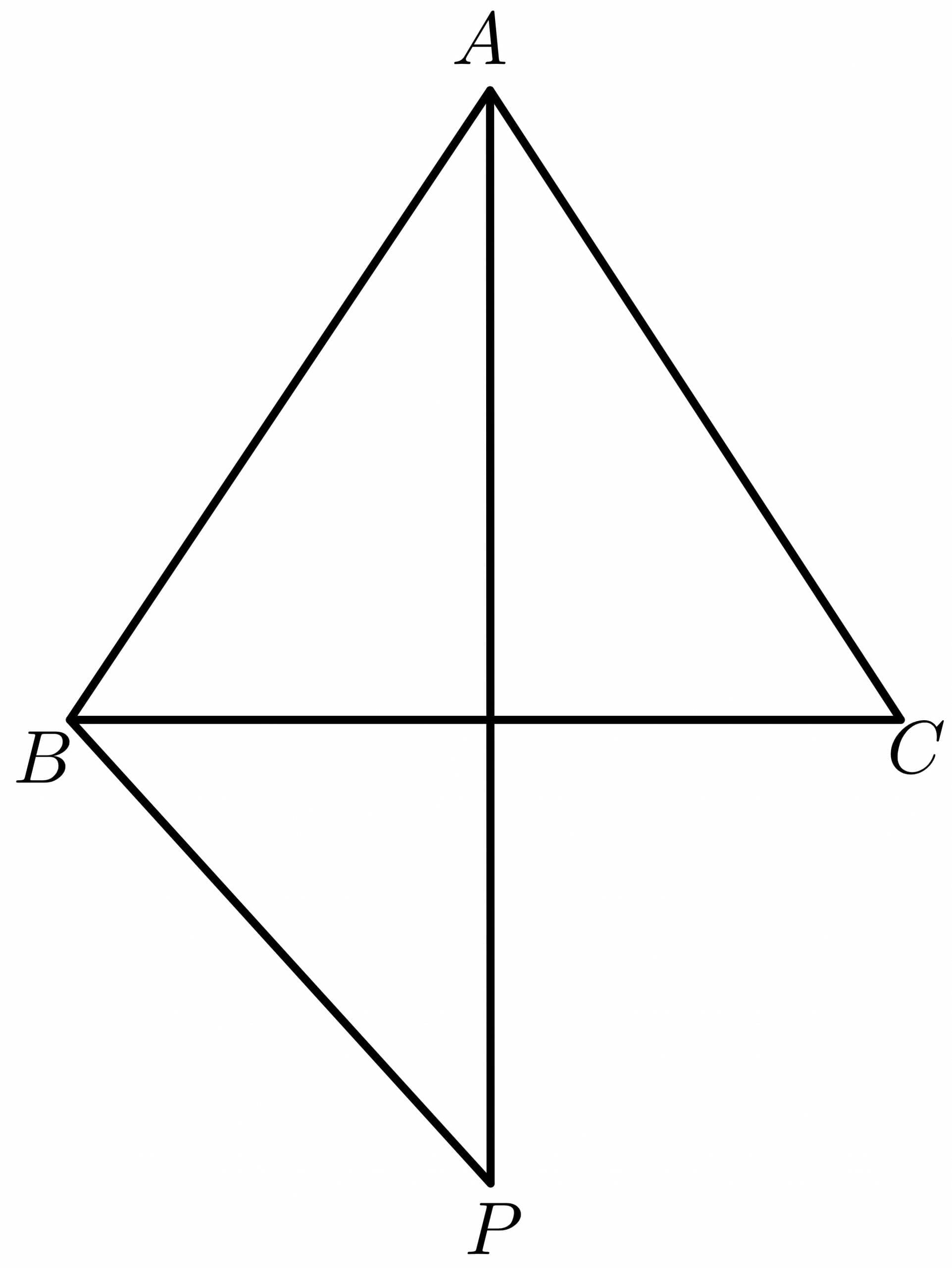
Prove that $PA > AC$, if $PB \cong BC$

Proof of Converse of Hinge Theorem

If two sides of the two triangles are congruent, then the triangle whose third side is longer will have the larger interior angle. So, in the converse theorem, we identify two congruent sides of the given triangles and prove that the interior angle of that triangle is larger, whose third side is longer than the other triangle.

For the converse theorem, we will adopt an indirect proof approach, i.e., proof by contradiction as described below:

Consider two triangles $\triangle ABC$ and $\triangle XYZ$.

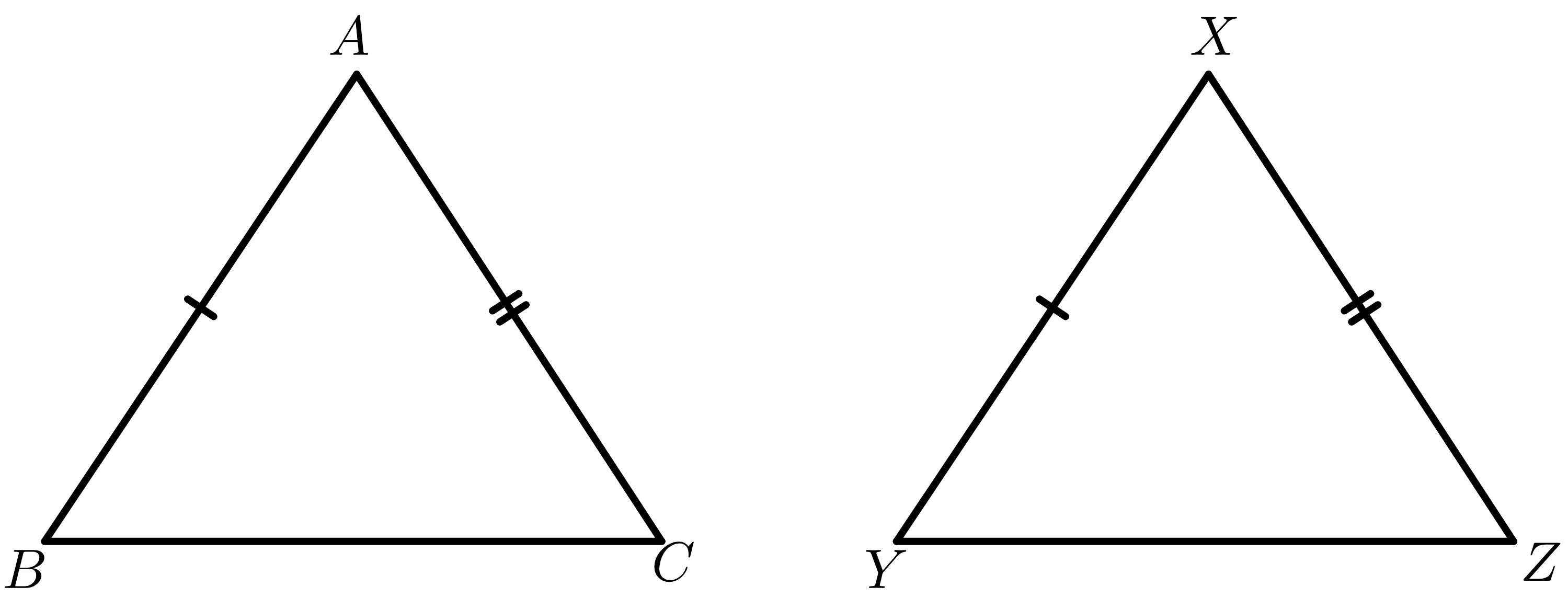
Given:

$AB \cong XY$

$AC \cong XZ$

$BC > YZ$

Prove:

We have to prove $m\angle A > m\angle X$

We will take two false assumptions and then draw a contradiction against them.

Assumption 1:

If $m\angle A = m\angle X$, then we can say that $m\angle A \cong m\angle X$.

The two sides of the triangles are already equal or congruent to each other. Then by S.A.S. postulate, we can say that $\triangle ABC \cong \ XYZ$, but that is against our given statement, which states that the side $ BC> YZ$ and hence both triangles are not congruent to each other.

So, by using assumption $1$, we concluded that $\triangle ABC \cong \ XYZ$ and $BC = YZ$.

$ BC =YZ$ (against the given statement and hence it is not true).

Assumption 2:

If $m\angle A < m\angle X$, then by the definition of Hinge theorem $ BC < YZ$

By the statements above, we know that $ AB =XY$ and $ AC = XZ$ and by Hinge theorem definition, the third side of the triangle that has the greater interior angle would be longer. In our assumption, $m\angle X > m\angle A$, hence side $ YZ> BC$.

The conclusion is that side $ Y.Z.> BC$ is against our given statement $ B.C.> YZ$, hence, a contradiction is drawn.

We have considered two cases where $m\angle A$ is either equal or less than $m\angle X$ and both have been proven false, so the only true condition is $m\angle A > m\angle X$.

Hence, we have proven that $m\angle A > m\angle X$.

Applications of Hinge Theorem

The primary application of the Hinge theorem is studying triangle inequalities. It can be used to tell the proximity of objects/items if they are forming a triangular shape.

Hinge theorem and converse Hinge theorem are used by civil engineers during their surveying of lands, where they try to figure out the estimated length of certain areas.

Example 1: 

If you are given two triangles \triangle ABC and \triangle XYZ with the following data:

$AB \cong XY$

$AC \cong XZ$

$BC = 14$ inches

$m\angle A = 45 ^{o}$

$m\angle X = 60^{o}$

 Choose the correct value of the side $YZ$ from the values given below.

$9$ inches, $10$ inches, $15$ inches, and $5$ inches.

Solution:

Through the Hinge theorem, we know that the triangle that has a greater interior angle will have the longer third side as compared to the other triangle. So in this case, the length of the side $YZ$ should be greater than that of side $BC$ as $m\angle X$ is greater than $m\angle A$. Hence, the value of $YZ$ is 15.

$YZ = 15$ inches.

Example 2:

If you are given two triangles $\triangle ABC$ and $\triangle XYZ$ with the following data:

$AB \cong XY$

$AC \cong XZ$

$BC = 14$ inches

$YZ = 9$ inches

$m\angle A = 45 ^{o}$

 Choose the correct value of $m\angle X$ from the values given below.

$50^{o}$, $60^{o}$, $70^{o}$ and $30^{o}$.

Solution:

Through the converse Hinge theorem, we know that the triangle that has a longer third side as compared to the other triangle will have a larger interior angle. In this case, the length of the side $BC$ is greater than that of side $YZ$, hence the $m\angle X$ should be less than that of $m\angle A$.

$m\angle X = 30^{o}$

Example 3: 

You are required to find the restriction on the value of “x” by using the Hinge theorem for the figure given below.

Solution:

We have been given two triangles, $\triangle ABC$ and $\triangle XBC$.

Where:

$AB \cong BX$

$BC \cong BC$

$XC = 5 cm$

$m\angle ABC = 60^{o}$ while $m\angle XBC = 50^{0}$

As the $m\angle ABC$ is greater than that of $m\angle XBC$, hence the value of “$x$” should be greater than $5$ cm.

$x > 5cm$

Example 4:

You are required to find the restriction on the value of “x” by using the Hinge theorem for the same figure as given in example 3. The only change is that $XC = x+7$ and $AC = 4x – 8$

Solution:

We have been given two triangles, \triangle ABC and \triangle XBC.

Where:

$AB \cong BX$

$BC \cong BC$

$XC = x + 7 cm$

$AC = 4x – 8$

$m\angle ABC = 60^{o}$ while $m\angle XBC = 50^{0}$

As the $m\angle ABC$ is greater than that of $m\angle XBC$, hence the side $AC$ should be greater than the side $XC$

$4x – 8 > x + 7$

Subtracting “$x$” from both sides:

$3x – 8 > 7$

Adding “$8$” on both sides:

$3x > 15$

Dividing both sides by “$3$”:

$x > 5$

Practice Questions:

1. Two triangles, $\triangle ABC$ and $\triangle XBC$, are given such that $ AB \cong XC$ and $ BC\cong BC$. You are required to compare the $m\angle XCB$ and $m\angle ABC$ using the Hinge theorem.

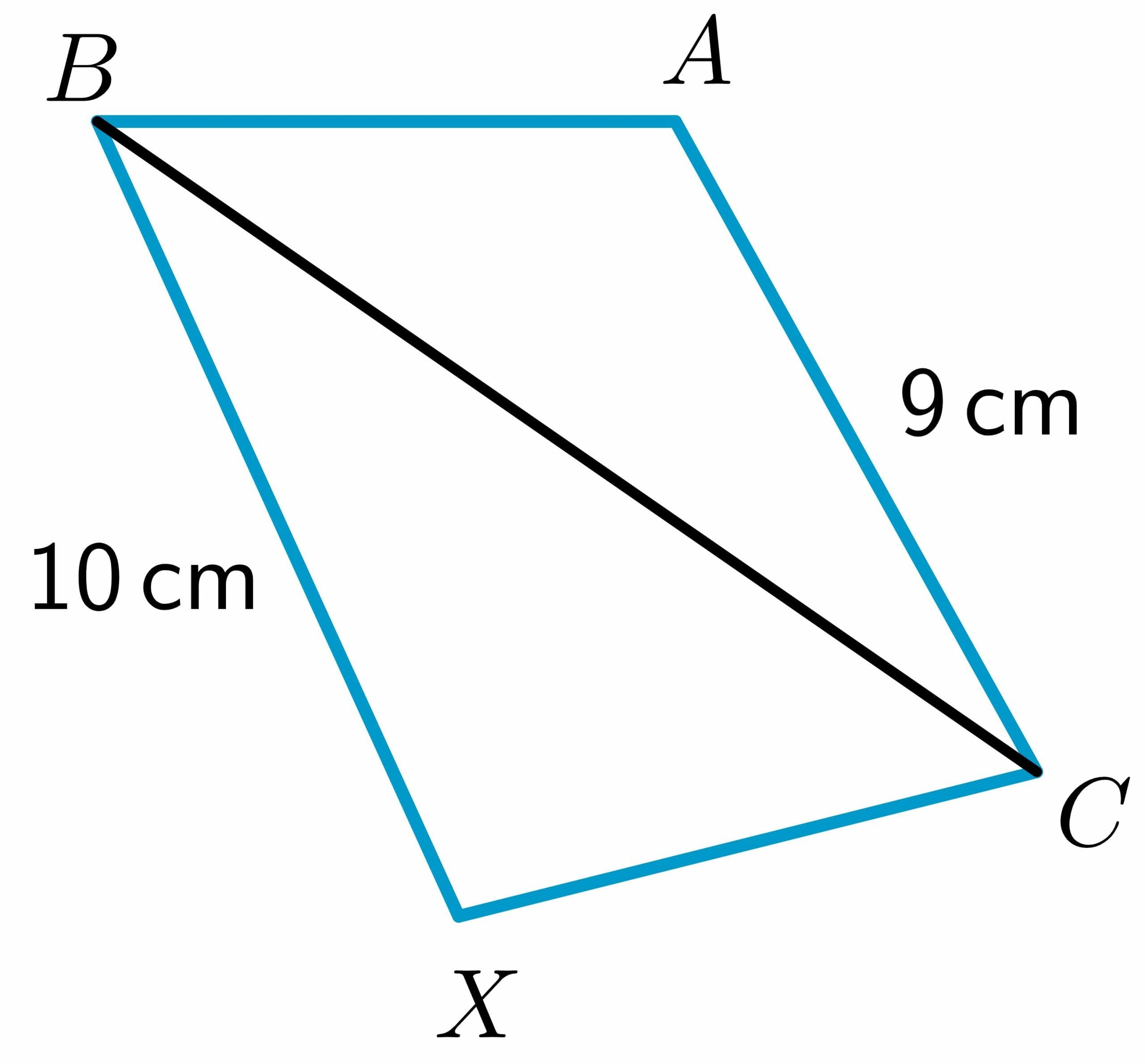
2. Two triangles, $\triangle ABC$ and $\triangle XBC$, are given such that $ AB \cong BX$. You are required to compare the side $CX$ and $AC$ using the converse Hinge theorem.

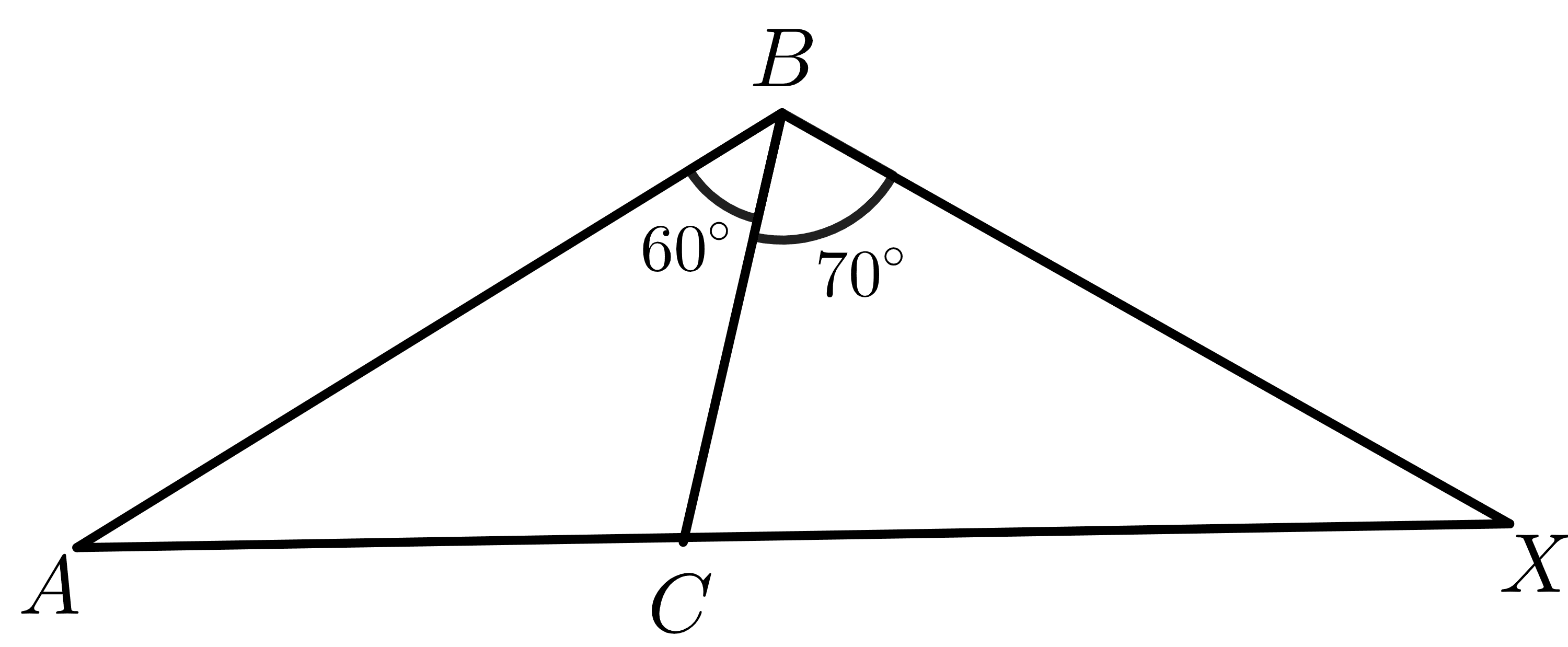
Answer Key:

1.

The length of two sides $BX$ and $AC$ is given as $10$ cm and $9$ cm respectively, while the side $AB$ is equal to $XC$ and $ BC\cong BC$ by reflexive property. Then through the Hinge theorem, the triangle having the longer third side will have the larger interior angle. Hence, $m\angle XCB > m\angle ABC$.

2.

The measure of two angles $m\angle ABC$ and $m\angle XBC$ are given as $60^{o}$ and $70^{o}$, respectively, while $ AB\cong BX$ and $ BC \cong BC$ by reflexive property. Then by the converse Hinge theorem, the triangle having a larger interior angle will have a longer length for the third side than other triangles. So in this case, the length of side $ AC < CX$.