JUMP TO TOPIC

Welcome to exploring the fundamental principles of geometry, focusing on the intriguing concept of points that lie on the same line.
In this article, we’ll dive deep into the principles of lines in two-dimensional and three-dimensional spaces, the tests for the points that lie on the same line, essential theorems, and the pervasive influence of these concepts in modern geometry and real-world applications.
Definition
In geometry, when points lie on the same line, they are said to be collinear. Collinearity is a property that relates points and lines in a geometric space. If two or more points fall on the same straight line, they are known as collinear points.
For instance, in a two-dimensional plane, if you draw a straight line, any number of points along that line would be considered collinear. This is because they all share the same line of reference. In three dimensions, the concept stays the same; if you can connect all the points using a single straight line, they are considered collinear. The word “collinear” comes from the Latin “col” (meaning “together”) and “linear” (meaning “line”), directly illustrating this concept.
This concept is a foundational aspect of many principles in geometry and is utilized in many real-world applications, from architectural design to satellite navigation systems.
Figure-1.
Properties
Points that lie on the same line, also known as collinear points, have several key properties. Here are some of the most notable properties:
Unlimited Number of Points
A line can have an infinite number of points. As long as these points are located on the same straight line, they are considered collinear.
Two Points Form a Line
Any two points in space will always form a line; thus, by definition, any two points are always collinear.
Three or More Points
When dealing with three or more points, collinearity becomes less trivial. Three or more points are collinear if they all lie on the same straight line.
Measure of Collinearity
We can determine if three points are collinear in a two-dimensional plane by examining the slopes between each pair of points. If the slopes are equal, the points are collinear.
In three dimensions, one common method is to calculate the area of the triangle formed by the points; if the area is zero, the points are collinear.
Order of Points
The order of points does not affect collinearity. For example, if points A, B, and C are collinear, it doesn’t matter whether B is between A and C or if C is between A and B. They remain collinear.
Distance
The distance between any two points is the shortest along the line on which the points lie.
Line Segments
When three or more points are collinear, the line segment connecting the two extreme points equals the sum of the line segments connecting the intermediate points.
Exercise
Example 1
Are the points A(2,3), B(4,6), and C(6,9) collinear?
Solution
We can find the slopes between AB, BC, and AC. If they are equal, then the points are collinear.
Slope AB = (6-3)/(4-2) = 1.5
Slope BC = (9-6)/(6-4) = 1.5
Slope AC = (9-3)/(6-2) = 1.5
All three slopes are equal, so points A, B, and C are collinear.
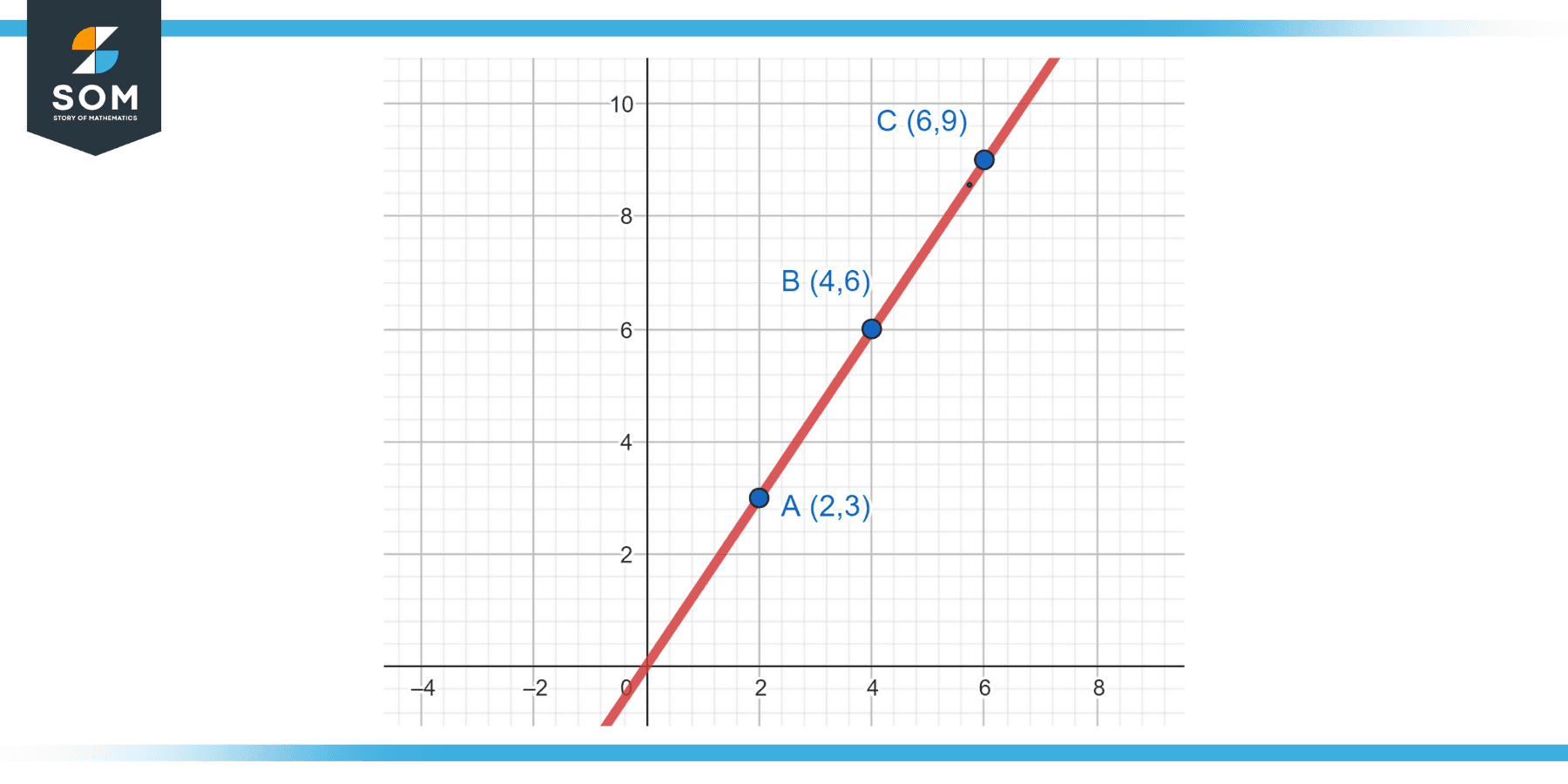
Figure-2.
Example 2
Are the points A(-1,-2), B(0,0), and C(3,6) collinear?
Solution
Again, we find the slopes:
Slope AB = (0-(-2))/ (0-(-1)) = 2
Slope BC = (6-0)/(3-0) = 2
Slope AC = (6-(-2))/(3-(-1)) = 2
Since the slopes are equal, the points A, B, and C are collinear.
Example 3
Are the points A(2,4), B(5,7), and C(10,12) collinear?
Solution
We find the slopes:
Slope AB = (7-4)/(5-2) = 1
Slope BC = (12-7)/(10-5) = 1
Slope AC = (12-4)/(10-2) = 1
The slopes are equal, so the points A, B, and C are collinear.
Example 4
Are the points A(-2,-3), B(-1,-2), and C(-3,-5) collinear?
Solution
We find the slopes:
Slope AB = (-2-(-3))/(-1-(-2)) = 1
Slope BC = (-5-(-2))/(-3-(-1)) = 1.5
Slope AC = (-5-(-3))/(-3-(-2)) = 2
The slopes are not equal, so points A, B, and C are not collinear.
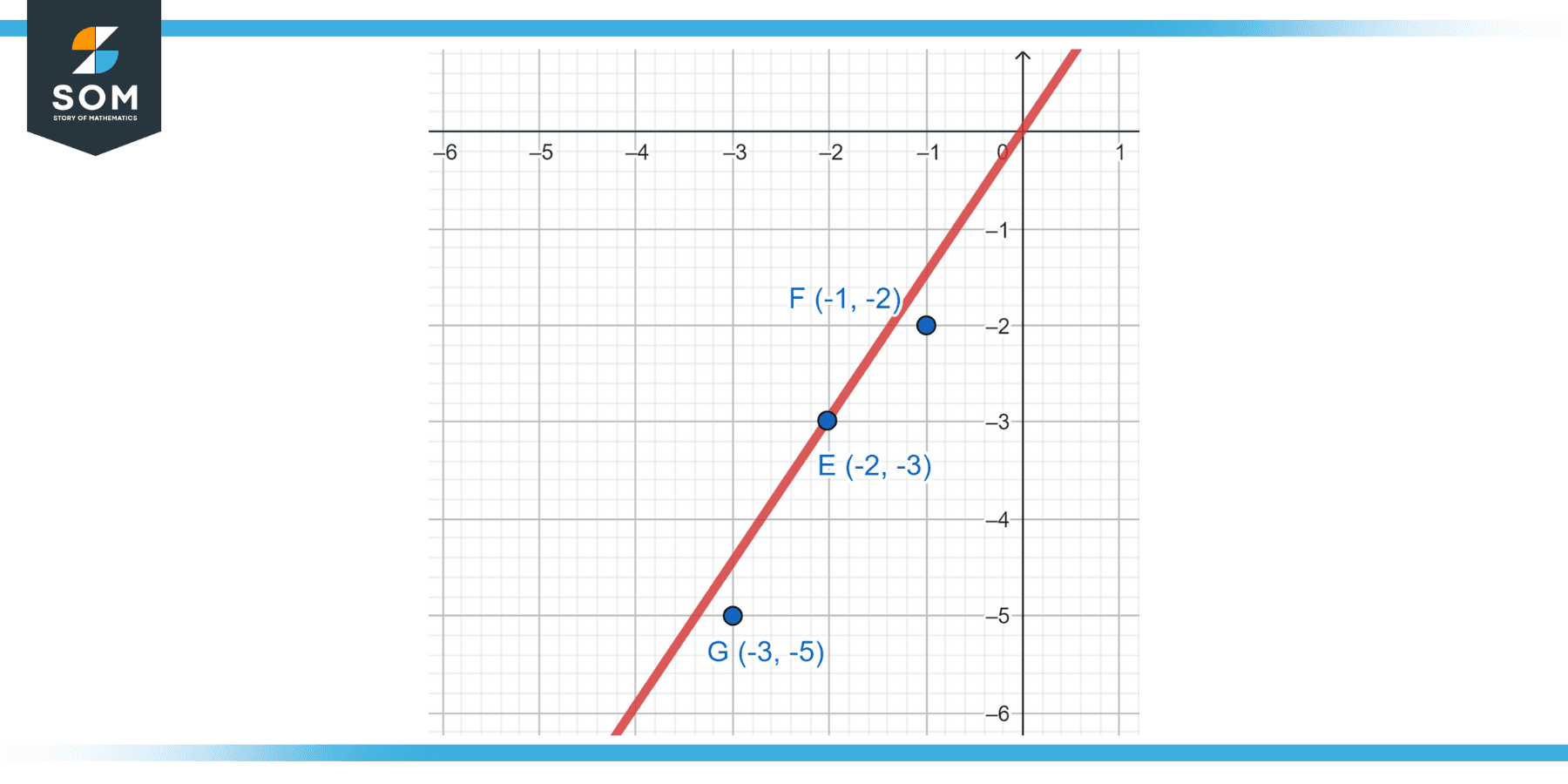
Figure-3.
Applications
The concept of points that lie on the same line, or collinearity, is foundational to many areas of study and industry. Here are a few examples of its wide-ranging applications:
Computer Graphics and Design
In this field, the principles of lines and points are fundamental for creating visual content. The understanding of points and lines helps in creating geometric shapes, digital illustrations, 3D modeling, and animation. Collinearity can be used in algorithms for line drawing, polygon filling, and more.
Physics
In physics, particularly in mechanics, the concept of collinear points is vital. For example, when analyzing motion in one dimension or forces acting along the same line, collinearity is a key consideration.
Engineering
In various branches of engineering, such as civil, structural, and mechanical engineering, the concept of collinear points is crucial. It helps in understanding structural integrity, force distribution, and alignment of different components of a machine or structure.
Astronomy and Space Science
Collinearity has important applications in celestial navigation and satellite placement. For example, collinear points in space are used to align telescopes with celestial bodies, or to align satellites in a ‘train’ to achieve constant coverage.
Geography and Geometric Surveying
In geographic information systems (GIS) and surveying, the concept of collinearity is used in identifying, representing, and manipulating spatial relationships between different geographic phenomena.
Machine Learning and Computer Vision
In the field of machine learning and particularly in computer vision, points lying on the same line (or more generally, geometric relationships between points) can be used for object recognition, image stitching for panorama creation, and 3D reconstruction from multiple images.
Robotics
In robotics, collinearity plays a significant role in motion planning and kinematics. Robots use this basic principle to calculate trajectories and to optimize movements.
Architecture and Urban Planning
In architecture and urban planning, points that lie on the same line are used to ensure the proper alignment of structures. This alignment can be critical for aesthetics, structural integrity, and functionality.
All images were created with GeoGebra.
