JUMP TO TOPIC
 Rolle’s theorem states that if a real-valued function is continuous in a closed interval $[a,b]$ and is differentiable on the open interval $(a,b)$ while $f(a) = f(b)$, then there must be a point “$c$” in the open interval $(a,b)$ such that $f'(c) = 0$.
Rolle’s theorem states that if a real-valued function is continuous in a closed interval $[a,b]$ and is differentiable on the open interval $(a,b)$ while $f(a) = f(b)$, then there must be a point “$c$” in the open interval $(a,b)$ such that $f'(c) = 0$.
The graphical representation of Rolle’s theorem is given below.
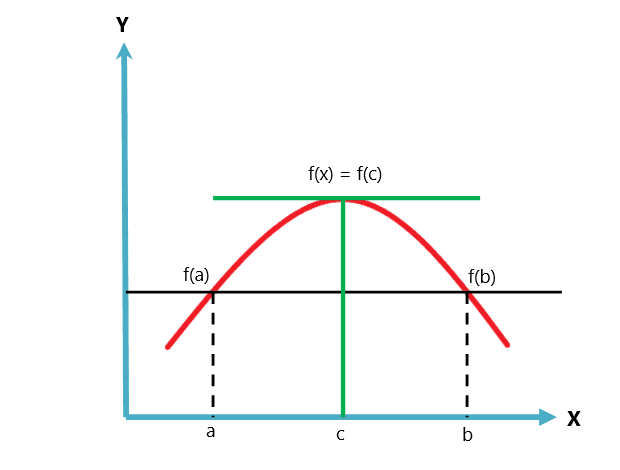
Rolle’s theorem is a variation or a case of Lagrange’s mean value theorem. The mean value theorem follows two conditions, while Rolle’s theorem follows three conditions.
This topic will help you understand Rolle’s theorem, its geometrical interpretation, and how it is different from the mean value theorem. We will also study numerical examples related to Rolle’s theorem.
What Is Rolle’s Theorem?
Rolle’s Theorem is a theorem stating that if a continuous function attains two equal values at two distinct or definite points, then there must be a point between those two points where the function’s derivative will be equal to zero. As stated earlier, Rolle’s theorem is a specific case of the mean value theorem or Langerange’s mean value theorem.
Before we study the graphical interpretation of Rolle’s theorem, it is instructive to know the difference between Rolle’s theorem and Lagrange’s mean theorem.
Rolle’s Theorem | Lagrange’s mean value theorem |
| The function “$f$” is continuous on a closed interval $[a,b]$ | The “$f$” function is continuous on a closed interval $[a,b]$ |
| The function “$f$” is differentiable on an open interval $(a,b)$ | The “$f$” function is differentiable on an open interval $(a,b)$ |
| If $f(a) = f(b)$, there exist a point “$c$” between a & b such that $f'(c) = 0$ | There exist a point “$c$” between a & b such that $f'(c) = \dfrac{f(a)\hspace{1mm} –\hspace{1mm} f(b)}{b\hspace{1mm}-\hspace{1mm}a}$ |
How To Use Rolle’s Theorem
Rolle’s theorem is simple to use; all we have to do is to satisfy all the three conditions which we have discussed earlier. Let us take a function $f (x) = x^{2}- 3x$ on a closed interval $[0,3]$ and see how we can use Rolle’s theorem on this function.
Here, $a = 0$ and $b = 3$ the end points of the interval.
Step 1:
The first step is to satisfy that function $f(x) = x^{2}\hspace{1mm}-\hspace{1mm} 3x$ must be continuous. A function is continuous if its graph is continuous without any breaks or jumps. We can see that $f(x)$ is a simple polynomial and all simple polynomial functions are continuous.
Step 2:
The function f(x) must be a differentiable function. All continuous functions can be differentiated. Since $f(x) = x^{2}\hspace{1mm}-\hspace{1mm} 3x$ is a continuous function, then it can be differentiated.
$f'(x) = 2x\hspace{1mm} –\hspace{1mm} 3$
Step 3:
The third step involves satisfying the condition $f(a) = f(b)$. So we will put the values of two end points in the function $f(x)$ and see if $f(a)$ and $f(b)$ are equal or not. If they are not equal, Rolle’s theorem cannot be applied.
$f(0) = (0)^{2}\hspace{1mm} – \hspace{1mm}3(0) = 0$
$f(3) = (3)^{2}\hspace{1mm} – \hspace{1mm}3(3) = 9\hspace{1mm} – \hspace{1mm}9 = 0$
Hence, $f(a) = f(b)$
Step 4:
The fourth and last step is to find a value “$x$” between $[a,b]$ that makes $f'(x) = 0$.
We know:
$f'(x) = 2x \hspace{1mm} –\hspace{1mm} 3$
So if $f'(x) = 0$, then
$2x – 3 = 0$
$2x = 3$
$x = \dfrac{3}{2}$
So $f'(x) = 0$ at $x = \dfrac{3}{2}$.
Proof of Rolle’s Theorem
Proof —- If a function ( real-valued) is continuous on a closed interval $[a,b]$ and differentiable on an open interval $(a,b)$, then there must be a point “$c$” ( that lies in between a and b) at which the derivative of the said function is zero.
To prove Rolle’s theorem, we will make use of two other theorems:
- Extreme value theorem states that if a function is continuous in a closed interval, it must have both a maxima and a minima.
- Fermat’s theorem states that the derivative of a function is zero at its maxima (or minima).
Now suppose a function (real-valued) is continuous on a closed interval $[a,b]$ and is differentiable on an open interval $(a,b)$. By extreme value theorem, it must have a maxima and minima in the closed interval $[a,b]$. Now suppose $f(a) = f(b)$, then the end points cannot possibly be both a maxima and a minima unless the function is a constant.
Hence, we have two possibilities:
1. We are given a constant function.
2. We are given a non-constant function.
Constant Function
The constant function just gives us a straight line, and in this case, every point satisfies Rolle’s theorem as the derivative of a constant function is zero.
Non-constant Function
For a non-constant function, by extreme value theorem, there must be at least one point $c$ in $[a,b]$, which is either the maxima or the minima of the function. In either case, by Fermat’s theorem, the value of the derivative must be zero at $c$, which proves Rolle’s theorem.
Applications of Rolle’s Theorem
Rolle’s theorem has various real-life applications. Some of them are given below.
1. We can use Rolle’s theorem to find a maximum or extreme point of a projectile trajectory of different objects.
2. Rolle’s theorem plays a vital role in constructing curved domes on the top of museums or other buildings.
3. It is extremely useful in determining the maximum values for complex graphical functions.
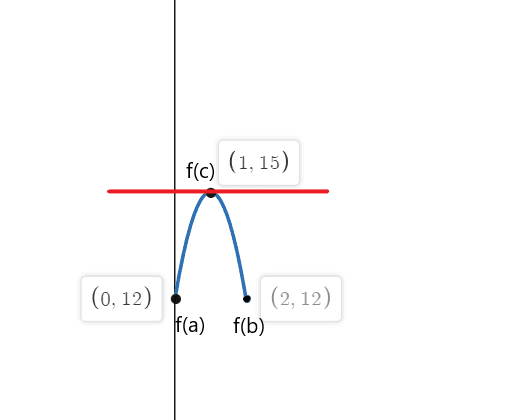
Example 1
Verify Rolle’s theorem for the function $f(x) = -3x^{2}+ 6x + 12$ on a closed interval $[0,2]$.
Solution:
The function is a simple polynomial function, so it is continuous in the interval $[0,2]$, and it is differentiable in the interval $(0,2)$.
Let us verify the third condition $f(a) = f(b)$.
$f(0) = -3(0)^{2}\hspace{1mm}+\hspace{1mm} 6(0) \hspace{1mm} +\hspace{1mm} 6 = 0\hspace{1mm} +\hspace{1mm} 0 \hspace{1mm}+ \hspace{1mm}12 = 12$
$f(2) = -3 (2)^{2}\hspace{1mm} +\hspace{1mm} 6(2) \hspace{1mm} +\hspace{1mm} 12$
$f(2) = -3 (4) \hspace{1mm} +\hspace{1mm} 12\hspace{1mm} +\hspace{1mm} 12$
$f(2) = -12\hspace{1mm} +\hspace{1mm} 12\hspace{1mm} +\hspace{1mm} 12 = 12 $
Hence $f(0) = f(3)$
Now let us calculate the value of “$x$” where $f'(x) = 0$.
$f'(x) = -6x\hspace{1mm} +\hspace{1mm} 6$
put $f'(x) = 0$
$-6x + 6 = 0$
$x = \dfrac{-6}{-6}$
$x = 1$
Hence, $x = 1$ is the tangent of the function where the slope is equal to zero.
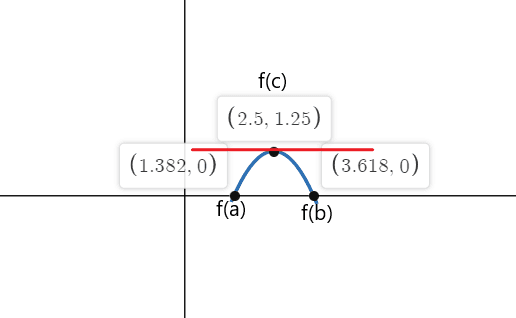
Example 2:
Verify Rolle’s theorem for the function $f(x) = – x^{2}+ 5x – 5$ on a closed interval $[1,4]$.
Solution:
The function is a simple polynomial function, so it is continuous in the interval $[1,4]$, and it is differentiable in the interval $(1,4)$.
Let us verify the third condition $f(a) = f(b)$.
$f(1) = – (1)^{2}\hspace{1mm}+\hspace{1mm} 5(1) \hspace{1mm} + \hspace{1mm}5 = -1\hspace{1mm} + \hspace{1mm}5 \hspace{1mm}- \hspace{1mm}5 = 4 \hspace{1mm}– \hspace{1mm}5 = -1$
$f(4) = -(4)^{2}\hspace{1mm}\hspace{1mm} +\hspace{1mm}5(4) \hspace{1mm} – \hspace{1mm}5$
$f(3) = -16\hspace{1mm} +\hspace{1mm} 20\hspace{1mm} –\hspace{1mm} 5$
$f(3) = 4\hspace{1mm} -\hspace{1mm} 5 = -1 $
Hence, $f(1) = f(4)$.
Now let us calculate the value of “x” where f'(x) = 0.
$f'(x) = -2x\hspace{1mm} +\hspace{1mm} 5$
put $f'(x) = 0$
$-2x\hspace{1mm} +\hspace{1mm} 5 = 0$
$x = \dfrac{-5}{-2}$
$x =\dfrac{5}{2}$
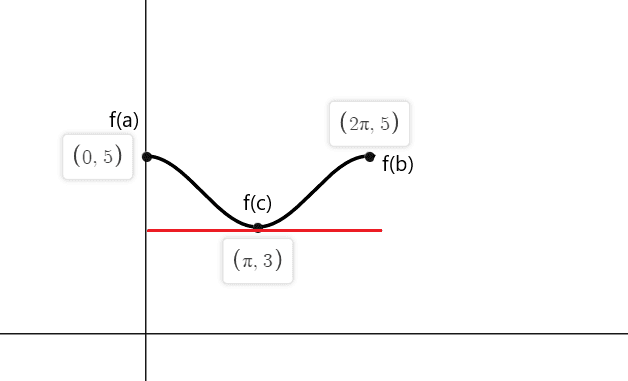
Example 3:
Verify Rolle’s theorem for the function $f(x) = cos(x) \hspace{1mm} +\hspace{1mm} 4$ on a closed interval $[0,2\pi]$.
Solution:
The function is continuous in the interval $[0,2\pi]$ and it is differentiable in interval $(0,2\pi)$. According to Rolle’s theorem, there must be at least one point “c” where $f'( c) = 0$ if $f(a) = f(b)$.
$f(0) = cos(0) \hspace{1mm} +\hspace{1mm} 4 = 1 \hspace{1mm}+\hspace{1mm} 4 = 5$
$f(2\pi) = cos(2\pi) \hspace{1mm} +\hspace{1mm} 4 = 1\hspace{1mm} +\hspace{1mm} 4 = 5$
$f'(x) = -sinx = 0$
-sinx is equal to zero at points $x_1 = 0$, $x_2 = \pi$ and $x_3 = 2\pi$
So the tangents of the function f(x) where slope is equal to zero at both of the end points are $a = 0$, $b = 2\pi$ and at $c = \pi$.
Example 4:
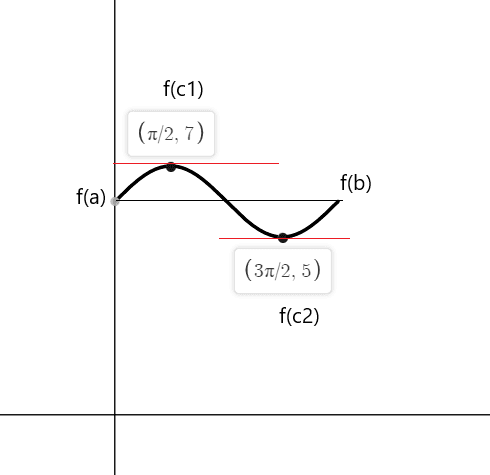
Verify Rolle’s theorem for the function $f(x) = sin(x) + 6$ on a closed interval $[0,2\pi]$.
Solution:
The function is continuous in the interval $[0,2\pi]$ and it is differentiable in interval $(0,2\pi)$. According to Rolle’s theorem, there must be at least one point “c” where $f'( c)$ = 0 if $f(a) = f(b)$.
$f(0) = sin(0) \hspace{1mm} +\hspace{1mm} 6 = 0 \hspace{1mm}+ \hspace{1mm}6 = 6$
$f(2\pi) = sin(2\pi) \hspace{1mm} +\hspace{1mm} 6 = 0\hspace{1mm} + \hspace{1mm}6 = 6$
$f'(x) = cos(x) = 0$
$cos(x)$ is equal to zero at points $c_1 = \dfrac{\pi}{2}$ and $c_2 = \dfrac{3\pi}{2}$
Example 5:
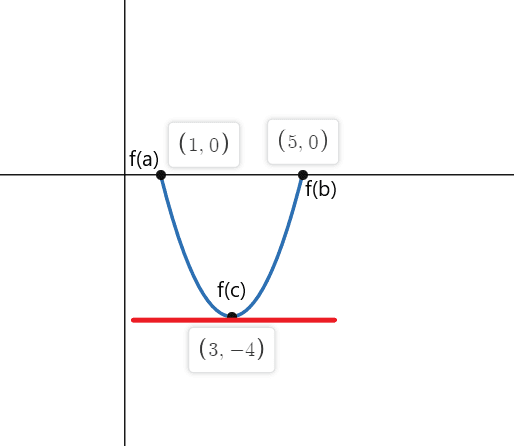
Verify Rolle’s theorem for the function $f(x) = x^{2}-6x + 5$ on a closed interval $[1,5]$.
Solution:
The function is a simple polynomial function, so it is continuous in the interval $[1,5]$, and it is differentiable in the interval $(1,5)$.
Let us verify the third condition $f(a) = f(b)$.
$f(1) = (1)^{2}\hspace{1mm}- \hspace{1mm}6(1) \hspace{1mm} + \hspace{1mm}5 = 1\hspace{1mm} – \hspace{1mm}6 +\hspace{1mm} 5 = 5\hspace{1mm} –\hspace{1mm} 5 = 0$
$f(5) = (5)^{2} – 6(5) + 5$
$f(3) = 25\hspace{1mm} – \hspace{1mm}30\hspace{1mm} +\hspace{1mm} 5$
$f(3) = -5\hspace{1mm} +\hspace{1mm} 5 = 0$
Hence $f(1) = f(5)$
Now let us calculate the value of “$x$” where $f'(x) = 0$.
$f'(x) = 2x – 6$
put $f'(x) = 0$
$2x – 6 = 0$
$x = \dfrac{6}{2}$
$x = 3$.
Practice Questions
1. Which of the following functions satisfy all the three conditions of Rolle’s theorem?
- $f(x) = sin(2x)$ on a closed interval $[0,2\pi]$
- $f(x) = |x-4|$ on a closed interval $[0,8]$
- $f(x) = |cos(2x)|$ on a closed interval $[0,\pi]$
- $f(x) = \dfrac{1}{x^{4}}$ on a closed interval $[0,2]$
2. Verify Rolle’s theorem for the function $f(x) = x^{2}\hspace{1mm}-\hspace{1mm} 5$ on a closed interval $[-4 , 4]$.
Answer Keys:
1.
- $Sin(2x)$ is continuous on closed interval $[0,2\pi]$ and differentiable on open interval $(0,2\pi)$ and $f(0) = f(2\pi ) = 0$. Hence, it satisfies all the conditions of Rolle’s theorem.
- $f(x)=|x-4|$ gives us a V- shaped graph and we have a vertex at $x = 4$. So this function cannot be differentiated and it does not satisfies all the conditions of Rolle’s theorem.
- The function $f(x)= |cos(2x)|$ is not differentiable at $x = \dfrac{\pi}{2}$. Hence, it does not satisfy all the conditions of Rolle’s theorem.
- The function $f(x) = \dfrac{1}{x^{4}}$ gives an indefinite value at $x = 0$, so it is not a continuous function. Hence, this function does not satisfy all the conditions of Rolle’s theorem.
2.
The function is a simple polynomial function, so it is continuous in the interval $[-4,4]$, and it is differentiable in the interval $(-4,4)$.
Let us verify the third condition $f(a) = f(b)$.
$f(-4) = (-4)^{2}\hspace{1mm}-\hspace{1mm} 5 = 16 – 5 = 11$
$f(4) = (4)^{2}-\hspace{1mm} 5 = 16\hspace{1mm} –\hspace{1mm} 5 = 11$
Hence, $f(-4) = f(4)$
Now let us calculate the value of “$x$” where $f'(x) = 0$.
$f'(x) = 2x$
put $f'(x) = 0$
$2x = 0$
$x = 0$
