JUMP TO TOPIC
 A prime polynomial or irreducible polynomial is a type of polynomial with integer coefficients that cannot be factorized into polynomials of lower degree with integer coefficients.
A prime polynomial or irreducible polynomial is a type of polynomial with integer coefficients that cannot be factorized into polynomials of lower degree with integer coefficients.
Engineers, designers and architects have to deal with complex calculations on a daily basis, and most of the calculations involve polynomials. Polynomials are used in predicting different economic models and determining different traffic patterns, so it has vast applications in our daily life.
There are different types of polynomials, and in this topic, we will study the prime or irreducible polynomial in detail along with numerical examples.
What Is a Prime Polynomial?
The polynomials which cannot be factorized into lower degree polynomials with integer coefficients are called prime/irreducible polynomials. The irreducible polynomials properties will depend upon the nature and types of coefficients of the polynomial.
Polynomials
To understand the concept of prime polynomial, first we must understand what a polynomial is and how we factorize a polynomial. Polynomial is a word that is derived from two greek words, “Poly” and “Nomial.” “Poly” and “Nomial” mean “Many” and “Terms,” respectively. So the word polynomial means many or multiple terms.
In mathematics, an algebraic or mathematical expression consisting of variables and coefficients is known as polynomials. The variables in a polynomial can have exponents that are whole numbers only, e.g., $x^2 + 1$ is a polynomial but $x^{-1} + 1 = \frac{1}{x} + 1$ is not a polynomial.
For example, which of these is a prime polynomial: $x^3-1$ or $x^{2}+ 1$? The expression which cannot be factorized will be prime polynomial. In this case, we know we can write $x^{3}-1 = (x)^{3}-(1)^{3} = (x+1) (x^{2} +1 -x)$, but we cannot factorize $(x^{2}+ 1)$, so it is a prime polynomial.
Let’s consider an example of a polynomial with one variable, i.e., $2x^{2}+ 3x$. In this example, we have two terms, $2x^{2}$ and $3x$. The coefficient for the first term is “$2$”, and the coefficient for the second term is “$3$”. Similarly, $3x^{2}+5x+ 6$ is a polynomial with three terms; in this example, the coefficient of the first term is “$3$” while the coefficient of the second term is “$5$”, and finally, the number “$6$” is a constant.
Now that we know what a polynomial is. Let us study some types of polynomials.
- Monomial
- Binomial
- Trinomial
Monomial: An expression containing only a single or one non-zero term will be deemed a monomial. For example, $4x$, $5x$, $5x^{2}$ all are monomials.
Binomial: An expression containing two terms separated by a subtraction or addition sign will be called binomial. For example, $4x +3$ , $5x-6$, $5x^{2}+8$ all are binomials.
Trinomial: An expression which contains exactly three terms is called trinomial. All three terms are separated by a minus or addition sign. For example, $4x+3y -2$, $5x^{2}+6x+1$, $5x^{2}+3y+4$ all are trinomials.
Factorization of a Polynomial
There are different methods of factorization, namely the Greatest common factor (GCF), the difference in square, grouping and sum or difference of cubes. What is common in all these techniques is to divide the expression into factor polynomials. While doing factorization, we split the given expression in such a manner that when we multiply all the factors, it gives us the original expression or polynomial. We carry on doing factorization until the polynomial is factorized completely or until all factors become irreducible polynomials.
For example, if we are given the number 16 and we have to factorize it, we can write it as:
$16 = (8) (2)$
$16 = (4) (4)$
$16 = (\dfrac{1}{2})(32)$
$16 = ( -2) (-8 )$
Similarly, we can factorize $x^{2}-16$ as $(x+4) (x-4)$ and $x^{4}-16$ as $(x^{2}+4) (x^{2}- 4) = (x^{2}+4) (x+2) (x-2)$. So we can see that if we multiply the factorized expressions, then it will give us the original polynomial function.
We have discussed in detail what a polynomial is and how it can be factorized. Let us now study the polynomials that cannot be factorized, i.e., the irreducible polynomials.
How To Find Prime Polynomials
The prime or irreducible polynomials are just like the prime numbers. For example, we know that the number $7$ is a prime number, and it cannot be reduced to smaller factors; similarly, the polynomial $a^{2}-3$ is an irreducible polynomial, and it also cannot be factorized into polynomials of smaller degrees. But there is a subtle point to consider here.
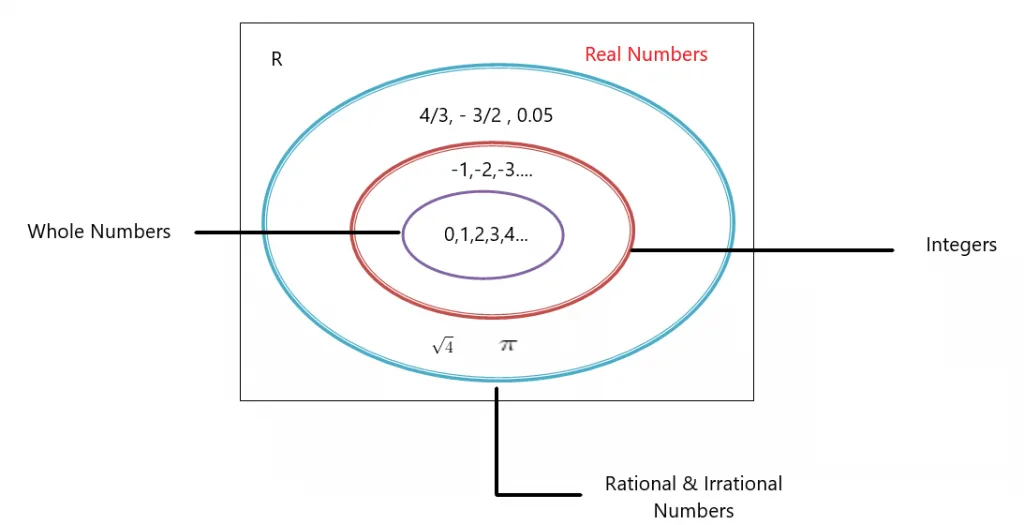
The number $7$ can actually be written as $(3+\sqrt{2}) (3-\sqrt{2})$. We can say that $(3+\sqrt{2}) (3-\sqrt{2})$ are the factors of number $7$ and similarly the polynomial $a^{2} – 3$ can also be factorized as $(a+\sqrt{3}) (a-\sqrt{3})$. So we must be specific while mentioning the domain where the polynomial is a prime/irreducible polynomial. A polynomial may be prime if its coefficients are restricted to some set of numbers (e.g. integers or rational numbers) but it may be reducible if the coefficients are allowed to be in another set (e.g. Real or complex numbers). The difference between different sets of numbers is depicted in the figure below:
Prime Polynomial Irreducibility Tests
A polynomial can be prime or irreducible over one field, and it can be reducible over a different field. We have discussed the example of $a^{2} – 2$. It was irreducible if the coefficient domain was in Z and reducible if the domain was R.
So now we know that every irreducible polynomial is not an irreducible polynomial over all possible fields. There are some irreducibility tests for polynomials. Some of the tests will depend upon the degree of polynomials, while the other tests will depend upon the domain of the polynomial. The list of different tests or prime polynomial checkers is given below.
- Linear factor test
- Quadratic or Cubic factor test
- Brute Force Test
- Eisensteins Criterion Method
- Mod – p irreducibility Test
- Complex field test or complexify
- P Cyclotomic Method
Linear Factor Test: A polynomial will contain a factor over a field of the integer if it has a root in a rational number. Otherwise, it will be irreducible.
Quadratic/Cubic Function Test: Any function with a degree of $2$ or $3$ will only be reducible if the roots exist. If a function has no roots while having a degree of $2$ or $3$ will always be irreducible.
Brute Force Test: This is one of the most used methods to check the irreducibility of the polynomial. In this method, we write down all the possible factors of the given function and then verify whether or not the factors lie in the domain or mod of $Z_{n}$. For example, we are given a polynomial $4x^{4}+ 3x + 6$, and we have to check whether it is irreducible at $Z_2$. Then, we will check for all the possible factors, and if none of the possible factors is actual factors of the polynomial, then we will say that the polynomial is irreducible.
Eisenstein’s Criterion Method: Eisenstein’s criterion is used to check the reducibility of a polynomial. This method has some limitations and cannot be applied to all polynomials. It can be used to prove that any polynomial is irreducible if it cannot be factorized as a product of lower-degree polynomials.
Suppose we have a polynomial function $f(x)$.
$f(x) = a_{n}x^{n} + a_{n-1}x^{n-1}+ a_{n-2}x^{n-2} + …..+ a_{1}x + a_0$
Let’s say the function variable “x” can only be a rational number, and we can write f(x) as Q(x) while the coefficients are integers.
Now according to Eisenstein’s criterion, if there exists a prime number “p” and it can divide all the coefficients (a) except the leading and last coefficient, then the function Q(x) will be irreducible over rational numbers as well as integers. The conditions can be written as
- The prime “$p$” divides every $a_{k}$ where $0 \leq k \leq n$ except
- The prime “$p$” should not divide $a_n$ and
- The prime $p^{2}$ should not divide $a_0$
If a polynomial satisfies the above-mentioned condition, then the polynomial will be irreducible over the set of integers unless we have a scenario where all the coefficients $(a_k)$ have a common factor which is reducible.
Mod p Irreducibility Method: According to this method, if a polynomial cannot be factorized or it is irreducible over $Z_{p}$, then we will say that it is irreducible for the field $Z$.
P Cyclotomic Method: According to this method, if a polynomial function is given in the form $f(x) = x^{n-1} + x^{n-2} + x^{n-3}+….. x + 14$ where n is a positive integer. A polynomial in this form will be called a P Cyclotomic if $f(x)$ becomes Cyclotomic at n = p, where p is a prime number. Such a polynomial will be irreducible over $Q$.
Complex Test: If a polynomial function is given over the field of complex numbers $C$, then it will be irreducible only if the degree of the function is $1$. If the degree of any complex polynomial is greater than $1$, it will be reducible.
Let us now study different prime polynomial examples and verify the tests which we have discussed so far.
Example 1: Which expression is a prime polynomial 3m+9n or $x+4y^{2}$?
Solution:
We can factorize $3 m+9n$ as $3(m+3n)$ while we cannot factor $x+4y^{2}$, so $x+4y^{2}$ is a prime polynomial.
Example 2: Find out which of the following polynomials are irreducible and reducible over the fields of rational numbers, real numbers, complex numbers and integers.
a) $f(x) = x^{2}+ 6x + 9$
b) $f(x) = x^{2} – 4$
c) $f(x) = 4x^{2} – 2 = 2(\sqrt{2}x+1)( \sqrt{2}x-1)$
d) $f(x) = x^{2} – 3$
e) $f(x) = x^{2} + 1 = (x+i) (x-i)$
Solution:
a)
We can write the polynomial $f(x) = x^{2}+ 6x + 9$ as $x^{2}+ 6x + 9 = (x+3)^{2}$. This polynomial is reducible over the field of integers, real numbers, and rational and complex numbers. The coefficients of the polynomial can be integers, real or rational numbers, while we know that a polynomial is irreducible over the field of complex numbers only if the degree of the polynomial is $1$, and in this case, the degree of the polynomial is $2$ which is greater than 1.
b)
We can write the polynomial $f(x) = x^{2} – 4$ as $x^{2} – 4 = (x+2) (x-2)$. Just like the first polynomial, it is reducible over the field of integers, real numbers, rational numbers and complex numbers.
c)
We are given the polynomial $f(x) = 4x^{2} – 2$ and we can write it as $4x^{2} – 2 = 2(\sqrt{2}x+1)( \sqrt{2}x-1)$. As we can see, there are irrational coefficients in this polynomial. This polynomial will be irreducible over integers and rational numbers, while this will be reducible over real numbers and complex numbers.
d)
We can write the polynomial $f(x) = x^{2} – 3$ as $x^{2} – 3 = (x+ \sqrt{3})( x- \sqrt{3}) $. This polynomial will be irreducible over integers and rational numbers, while this will be reducible over real numbers and complex numbers
e)
We are given the polynomial $f(x) = x^{2} + 1$ which can also be written as $(x+i) (x-i)$. If the degree is greater than 1, then surely it is reducible over the complex numbers. This polynomial will not be reducible over the real numbers as the coefficients are imaginary numbers, and similarly, it will be irreducible over integers and rational numbers as well.
Example 3: Identify whether polynomial $f(x) = x^{2} -5x + 10$ is reducible or irreducible over the field of $Q$ using Eisenstein’s criterion
Solution:
We are given a function with the degree of 2, and we are asked to verify whether it is reducible or not by using Eisenstein’s criterion. We know that according to Eisenstein’s criterion, we have to find a prime number which divides the constant value of “10”. So, the prime numbers which can divide “$10$” are “$2$” and “$5$”.
Now we check for both prime numbers $2$ and $5$ and see whether or not they fulfil Eisenstein’s criterion. According to Eisenstein’s criterion, the prime number should not be able to divide the leading coefficient, and the square of the prime number should not be able to divide the constant term.
Let first prime number be $p_1 = 2$
Let first prime number be $p_2 = 5$
Leading coefficient $a_2 = 1$
$a_1 = 5$ and $a_0 = 10$
First Prime Number
The leading coefficient is not divisible by $p_{1}$, but the second coefficient $5$ is also not divisible by $p_{1}$, so the polynomial is reducible at this prime number.
Second Prime Number
The leading coefficient is not divisible by $p_{2}$, and the second coefficient $a_2$ is divisible by p_2, so it fulfils the first two criteria. The last criterion states that the square of a prime number should not be able to divide the constant term. The square of $p_2$ is $5^{2} = 25$ and the constant term $a_0 = 10$ is not divisible by $p_2$. Hence the given polynomial f(x) is not reducible over $Q$.
Example 4: Identify whether polynomial $f(x) = 3x^{4} -5x^{3} + 5$ is reducible or irreducible over the field of $Q$ using Eisenstein’s criterion
Solution:
We are given a polynomial $3x^{4} -5x^{3} + 5$. Let $a_4 = 3$, $a_3 = 5$, $a_2 = 0$, $a_1= 0$ and $a_0 = 5$. If a single prime is able to fulfill Eisenstein’s criterion, then we will say that the given polynomial is irreducible over the field of $Q$. So we take all those prime numbers which are able to divide the constant term. In this scenario, the only prime number that can divide $a_0$ is $5$.
The leading coefficient is not divisible by prime number $5$ while the other coefficient $a_3 =5$ is divisible by $5$ and the constant term $a_0 = 5$ is not divisible by the square of prime number $5$. Hence, it satisfies all the conditions of Eisenstein’s criterion, and the polynomial is irreducible over $Q$.
Example 5: Identify whether polynomial $f(x) = 3x^{2} -3x + 4$ is reducible or irreducible if $f(x)$ $\in$ $Z_{5}(x)$.
Solution:
We know that according to the quadratic/cubic method, a polynomial with a degree of $2$ or $3$ is reducible if there exists a single or more root. So, according to this definition, if there exists even a single root for our given polynomial in the mentioned field of integers, then the polynomial is reducible.
We are given the field $Z_{5}$, and we know that the elements of this field will be ${0,1,2,3,4}$. So we will check if any of these values make our given function or polynomial zero or not. If a value makes the polynomial zero, then it will be considered the root of the polynomial, and if none of these values in the field makes the polynomial zero, then we will conclude that the polynomial is irreducible for the given field.
Let us now put the values of integers and check for the reducibility of the polynomial.
$f(0) = 3(0)^{2} -3(0) + 4 = 0 – 0 + 4 = 4 \neq 0$
$f(1) = 3(1)^{2} -3(1) + 4 = 3 – 3 + 4 = 4 \neq 0$
$f(2) = 3(2)^{2} -3(2) + 4 = 9 – 6 + 4 = 7 \neq 0$
$f(3) = 3(3)^{2} -3(3) + 4 = 27 – 9 + 4 = 22 \neq 0$
$f(4) = 3(4)^{2} -3(4) + 4 = 81 – 12 + 4 = 73 \neq 0$
Hence the polynomial is irreducible over the field $Z_{5}(x)$
Example 6: Identify whether polynomial $f(x) = x^{3} -2x^{2} + 4$ is reducible or irreducible if $f(x)$ $\in$ $Z_{6}(x)$.
Solution:
The given polynomial has a degree of $3$, and hence it is a cubic function. As discussed earlier, any polynomial that has a degree of $2$ or $3$ will be irreducible if no root of the given polynomial exists in the given domain or field.
We are given the field $Z_{6}$, and we know that the elements of this field will be ${0,1,2,3,4,5}$. So we will check if any of these values make our given function or polynomial zero or not.
Let us now put the values of integers and check for the reducibility of the polynomial.
$f(0) = (0)^{3} -2(0)^{2} + 4 = 0 – 0 + 4 = 4 \neq 0$
$f(1) = (1)^{3} -2(1)^{2} + 4 = 1 – 2 + 4 = 3 \neq 0$
$f(2) = (2)^{3} -2(2)^{2} + 4 = 8 – 8 + 4 = 4 \neq 0$
$f(3) = (3)^{3} -2(3)^{2} + 4 = 27 – 18 + 4 = 15 \neq 0$
$f(4) = (4)^{3} -2(4)^{2} + 4 = 64 – 32 + 4 = 36 \neq 0$
$f(5) = (5)^{3} -2(5)^{2} + 4 = 125 – 50 + 4 = 79 \neq 0$
Hence, the polynomial is irreducible over the field $Z_{5}(x)$.
Example 7: Identify whether polynomial $f(x) = x^{4} + 2$ is reducible or irreducible if over $Q(x)$ and $C(x)$ by using brute force method.
Solution:
The given polynomial degree is $4$, and for this polynomial to be irreducible, then the degree of each factor of this polynomial should be less than 4 while the degree of both the factors should add up to be equal to $4$. In this brute force method, we have to factorize the given function f(x) into a product of two other factors. For example, if $f(x) = g(x).h(x)$.
Let us now factorize $f(x) = x^{4} + 2$.
$x^{4} + 2 = ((x^{2})^{2} + 2i) ((x^{2})^{2} – 2i)$
So, from the factors, we can conclude that the given polynomial is irreducible over Q(x) while it is reducible over $C(x)$.
Example 8: Identify whether polynomial $f(x) = x^{4}-3x^{2}+ 9$ is reducible or irreducible if over $Q[x]$.
Solution:
The given polynomial degree is $4$, so we cannot use the cubic or quadratic test. Next up, we can use Eisenstein’s criterion, and the prime number in this scenario will be p = 3, but it cannot be applied as it does not fulfill the last condition of Eisenstein’s criterion criteria as the square of constant term $9$ is divisible by the square of a prime number. So the only method left is the brute force method.
Let us factorize the given polynomial using completing the square method.
$x^{4}-3x^{2}+ 9 = (x^{2})^{2} + 3^{2} -3x^{2}$
Adding and subtracting $2x^{2}(3)$ on R.H.S
$x^{4}-3x^{2}+ 9 = (x^{2})^{2} + 3^{2} +2x^{2}(3) – 2x^{2}(3) – 3x^{2}$
$x^{4}-3x^{2}+ 9 = ((x^{2})^{2} + 3)^{2} – 2x^{2}(3) – 3x^{2}$
$x^{4}-3x^{2}+ 9 = ((x^{2})^{2} + 3)^{2} – 9x^{2}$
$x^{4}-3x^{2}+ 9 = ((x^{2})^{2} + 3)^{2} – (3x)^{2}$
$x^{4}-3x^{2}+ 9 = (x^{2} + 3 +3x) (x^{2} + 3-3x)$
$x^{4}-3x^{2}+ 9 = (x^{2} + 3x +3) (x^{2}-3x +3)$
So, as we were able to factorize the original polynomial into the product of two polynomials and the degree of both factorized polynomials is less than the original polynomial, hence the given polynomial $x^{4}-3x^{2}+9$ is reducible over $Q[x]$.
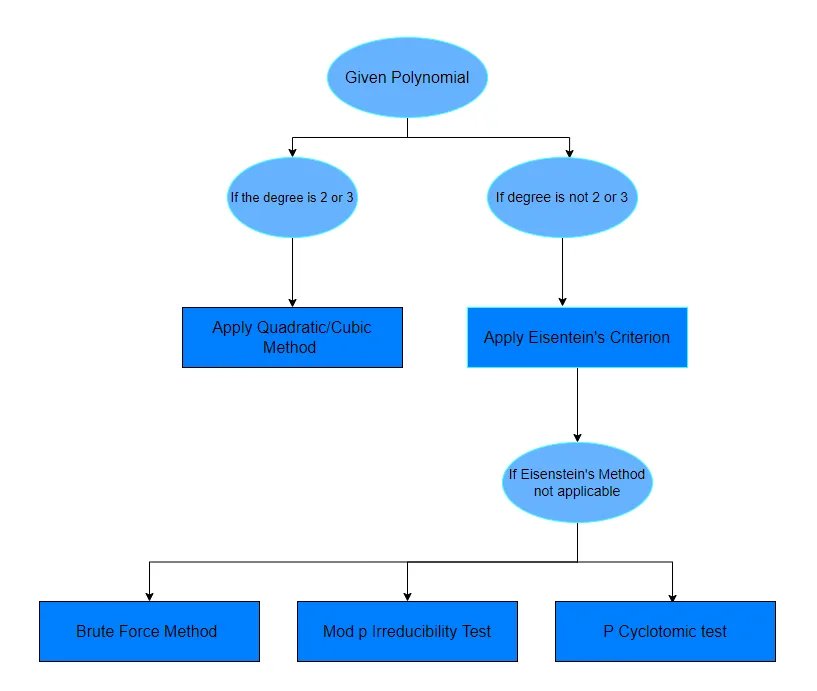
After studying the above examples, you will hopefully be feeling confident in finding out which polynomial is reducible or not. If a question does not specify a method to solve a given question, then you can just follow the chart given below.
Practice Questions:
a. Determine whether the expression 25y+1 is a prime polynomial.
b. Identify whether polynomial $f(x) = x^{4}+x + 1$ is reducible or irreducible if over $Q[x]$.
c. Identify whether polynomial $f(x) = x^{5}+ x^{4}+ x^{3}+ x^{2}+ x + 1$ is reducible or irreducible over $Q[x]$ by using P cyclotomic method.
d. Identify whether polynomial $f(x) = x^{4}+ x^{3}+ x^{2}+ x + 1$ is reducible or irreducible over $Q[x]$ by using P cyclotomic method.
Answer Key:
a)
This is just like a prime expression example as it has only two factors 1 and (25 y+1). Hence, it is a prime polynomial.
b)
We can factorize $x^{4}+x+1 = (x^{2}+ax+1)( x^{2}+bx+1)$
$ (x^{2}+ax+1) ( x^{2}+bx+1) = x^{4}+ bx^{3}+ x^{2}+ ax^{3}+abx^{2}+ax + x^{2}+bx +1$
$(x^{2}+ax+1) ( x^{2}+bx+1) = x^{4}+ (a+b)x^{3}+ (2+ab) x^{2}+ (a+b) x +1$
Now let us compare the coefficients
$x^{4}+ x+1 = x^{4}+ (a+b)x^{3}+ (2+ab) x^{2}+ (a+b) x + 1$
$0 = (a+b)x^{3}$ so, $a+b = 0$
While
$x = (a+b) x$ so, $(a+b) = 1$
As $(a+b) = 0$ and $a+b = 1$ both contradict themselves, hence $x^{4}+x+1$ is not reducible over $Q[x]$.
c)
We are given the polynomial $f(x) = x^{5}+ x^{4}+ x^{3}+ x^{2}+ x + 1$ and we can apply P- cyclotomic method on it.
We can write it as:
$f(x) = x^{6-1}+ x^{6-2}+ x^{6-3}+ x^{6-4}+ x^{6-5} + 1$
So in this example, n = 6 is not equal to a prime number; hence this polynomial is reducible over.
d)
We are given the polynomial $f(x) = x^{4}+ x^{3}+ x^{2}+ x + 1$ and we can apply P- cyclotomic method on it.
We can write it as:
$f(x) = x^{5-1}+ x^{5-2}+ x^{5-3}+ x^{5-4} + 1$
As $n =5$, which is a prime number, the given polynomial is irreducible.
