JUMP TO TOPIC
 The -90 degree rotation is the rotation of a figure or points at 90 degrees in a clockwise direction.
The -90 degree rotation is the rotation of a figure or points at 90 degrees in a clockwise direction.
Rotations are part of our life, and we see this phenomenon on daily basis. Some of the real-life examples of rotation are:
- Rotation of earth around its axis
- Rotation of car steering
- Rotation of characters in video games
- Rotation of Ferris Wheel in a theme park
- Rotation of camera lens while recording video
In mathematics, rotation of a point or function is a type of transformation of the function. In the rotation process, a graph or figure will retain its shape, but its coordinates will be swapped.
In this guide, we will discuss in detail what is meant by the rotation process and how we do a $-90^{o}$ rotation along with some numerical examples.
What Is a -90 Degree Rotation?
The -90 degree rotation is a rule that states that if a point or figure is rotated at 90 degrees in a clockwise direction, then we call it “-90” degrees rotation. Later, we will discuss the rotation of 90, 180 and 270 degrees, but all those rotations were positive angles and their direction was anti-clockwise. If we are required to rotate at a negative angle, then the rotation will be in a clockwise direction.
-90 Degree Rotation in Geometry
Let us first study what is 90-degree rotation rule in terms of geometrical terms. If a point is given in a coordinate system, then it can be rotated along the origin of the arc between the point and origin, making an angle of $90^{o}$. We rotate the point around the origin by maintaining the same distance from the origin, then we will call it the 90-degree rotation of that point along the origin. If the rotation is anti-clock-wise, then we call it 90-degree rotation, and if we say 90-degree rotation clockwise, then we call it negative 90 degree rotation.
We have studied the change in coordinates values when we rotate a figure or point in a counterclockwise direction, now let us see the resulting new points if we rotate a figure or point in a clockwise direction. Suppose we are given a point $(x,y)$, and we have to rotate this point about the origin $(0,0)$.
- When $(x,y)$ is rotated at $-90^{o}$ then the new point will be $(y, -x)$
- When $(x,y)$ is rotated at $-180^{o}$ then the new point will be $(-x,-y)$
- When $(x,y)$ is rotated at $-270^{o}$ then the new point will be $(-y, x)$
We can see that the sign of the coordinates in the case of -90 degree rotations is opposite to that of 90-degrees rotation.
Let us study this example of a polygon. So we have a polygon having three points A $= (8,6)$ B $= (4,2)$ and C $=(8,2)$. If we move this figure by $-90^{o}$, then the new points will be A $= (6,-8)$ B = (2,-4) and C = (2,-8). We can see from the figure below when we rotate the figure 90 degrees clockwise then the shape of the figure will remain the same, only the values x and y coordinates are swapped along with a change in the sign of the original y coordinate value.
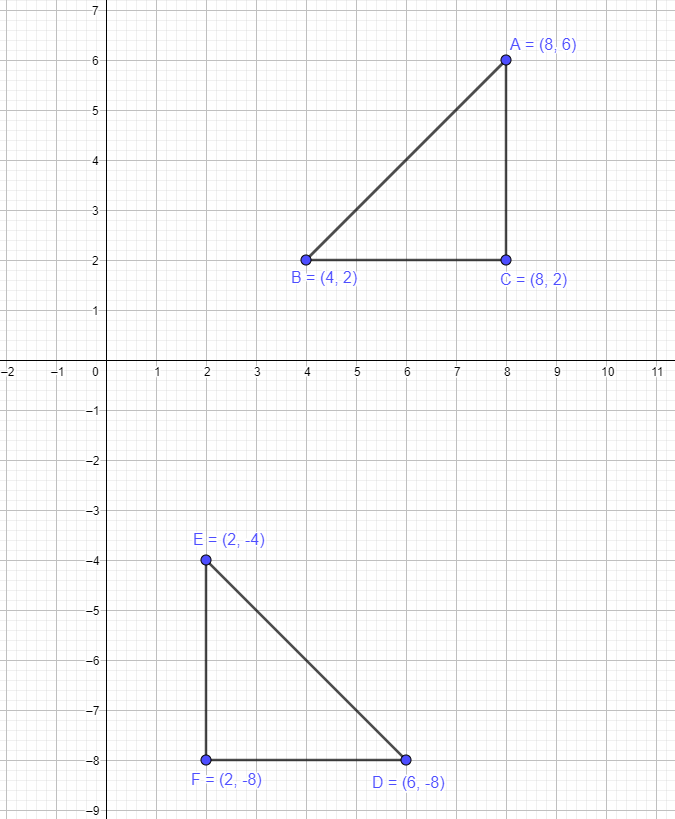
-90 Degree and 270-Degree Rotation
The -90 degree rotation or 90-degree clockwise rotation is the same as a 270-degree rotation anti-clockwise. If you revisit what we learned earlier in the section and compare it with the $-90^{o}$ rotation section, you can easily see that $-90^{o}$ rotation = 270-degree rotation, so if you rotate a point of figure 90 degrees clockwise or 270 degrees anti-clockwise, the result will be the same.
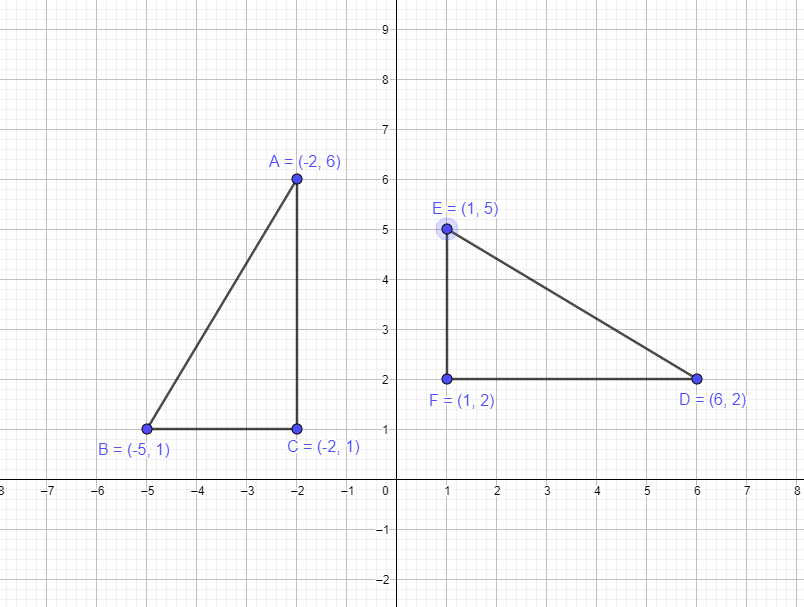
Example 1: Suppose a triangle ABC have the following coordinates A $= (-2,6)$, B $= (-5,1)$, C $= (-2,1)$. You are required to draw a new triangle DEF by rotating the vertices of the original triangle about the origin by $-90^{o}$.
Solution:
We have to rotate the figure of triangle ABC whose all vertices lie in the second quadrant so we know that when we rotate it 90 degrees clockwise, the whole triangle should be in the first quadrant, and the x and y coordinates of all the vertices should be positive. So, by applying the rule of $-90^{o}$ rotation we know that $(x,y)$ → $(y,-x)$. Hence the new coordinates will be:
- The vertex A $(-2,6)$ will become D $(6,2)$
- The vertex B $(-5,1)$ will become E $(1,5)$
- The vertex C $(-2,1)$ will become F $(1,2)$
The graphical representation of the original figure and the figure after rotation are given below.
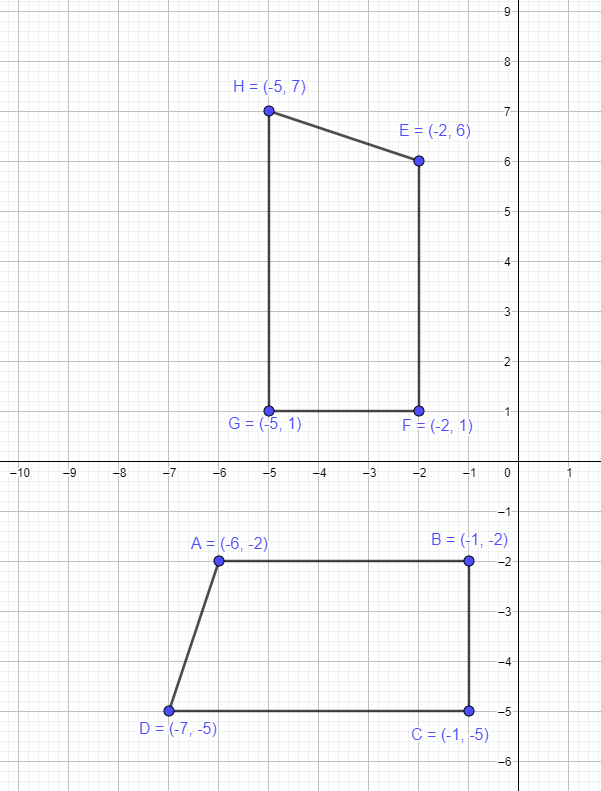
Example 2: Suppose a quadrilateral ABCD have the following coordinates A= $(-6,-2)$, B $= (-1,-2)$, C $= (-1,-5)$ and D $= (-7,-5)$. You are required to draw a new quadrilateral EFGH by rotating the vertices of the original triangle about the origin by $-90^{o}$
Solution:
We have to rotate the quadrilateral ABCD, whose all vertices lie in the third quadrant so we know that when we rotate it 90 degrees clockwise, the whole quadrilateral should move into the second quadrant, and all the vertices will have a negative x coordinate while positive y coordinate. So, by applying the rule of $-90$ degree rotation we know that $(x,y)$ → $(y,-x)$. Hence the new coordinates will be:
- The vertex A $(-6,-2)$ will become E $(-2,6)$
- The vertex B $(-1,-2)$ will become F $(-2,1)$
- The vertex C $(-1,-5)$ will become G $(-5,1)$
- The vertex D $(-7,-5)$ will become H $(-5,7)$
The graphical representation of the original figure and the figure after rotation are given below.
Example 3: Suppose you are given a polygon with vertices A $= (-5,3)$, B $= (-6,3)$ and C $= (1,3)$. The polygon is first rotated at $180^{o}$ clockwise, and then it is rotated $90^{o}$ clockwise. You are required to determine the value of coordinates after the final rotation.
Solution:
In this problem, we have to rotate the polygon two times. First, we have to rotate the polygon $180$ degrees clockwise, and the rule for that is $(x,y)$ → $(-x,-y)$
- The vertex A $(-5,3)$ will become D $(5,-3)$
- The vertex B $(-6,3)$ will become E $(6,-3)$
- The vertex C $(1,3)$ will become F $(-1,-3)$
Now we have to move the new polygon figure with vertices DEF $90$ degrees in a clockwise direction, and we know the rule for a $90$-degree clockwise direction is $(x,y)$ → $(y,-x)$
- The vertex D $(5,-3)$ will become G $(-3,-5)$
- The vertex E $(6,-3)$ will become H $(-3,-6)$
- The vertex F $(-1,-3)$ will become I $(-3,1)$
Rotations
A rotation is a type of transformation of a function or a graphical shape. There are four types of elementary transformations a) Reflection b) Rotation c) Translation d) Dilation. During the process of rotation, the shape or figure spins around a point in such a manner that the shape of the figure remains the same.
The rotation of a figure in a cartesian plane is usually carried around the origin and the figure can be rotated along the x and y axis in the four quadrants. Most commonly used rotations are $90^{o}$, $180^{0}$ and $270^{o}$ in a clockwise or counter-clockwise direction with respect to the origin $(0,0)$.
Quadrants
We know that a cartesian plane has four quadrants and each quadrant has a specific sign convention for the x and y coordinates.
- First Quadrant (+, +)
- Second Quadrant (- , +)
- Third Quadrant (-, -)
- Fourth Quadrant (+, – )
Let’s say we start with a point $(x,y)$ in the first quadrant. Now if this point does a 90-degree rotation, then we mean that the point will do a rotation at 90 degrees anti-clockwise then the resulting point will be $(-y, x)$.
Similarly, if we rotate the point 180 degrees then it will rotate at an angle of 180^{o} in an anti-clockwise direction then the resulting point will be $(-x,-y)$, and finally, if we do a 270-degree rotation then the point will rotate in an anti-clockwise direction at 270^{o} and the resulting point will be (y, -x). So we can write the rotation for the point $(x,y)$ in bullet form as:
- When $(x,y)$ is rotated at $90^{o}$ counter clockwise then the new point will be $(y, -x)$
- When $(x,y)$ is rotated at $180^{o}$ counter clockwise then the new point will be $(-x,-y)$
- When $(x,y)$ is rotated at $270^{o}$ counter clockwise then the new point will be $(-y, x)$
Let us now take an example of the point $(-3,4)$. We know that this point lies in the second quadrant, so when the point is rotated at 90 degrees, the new point will be $(-4,-3)$, and this point will lie in the third quadrant, as it is shown by the sign convention of new point. When the point $(-3,4)$ is rotated at $180^{0}$, the new point will be $(3,-4)$, and finally, when the point is rotated at 270 degrees then the new point will be $(4,3)$.
We have discussed an example related to a single point. Now, let us see an example involving a polygon with 3 points A $= (8,6)$ B $= (4,2)$ and C $=(8,2)$. If we move this figure by 90 degrees anti-clockwise, then all the three points move 90 degrees anti-clockwise, and the new points after the rotation will be A $= (-6,8)$ B $= (-2,4)$ and C $= (-2,8)$, as shown in the figure below.
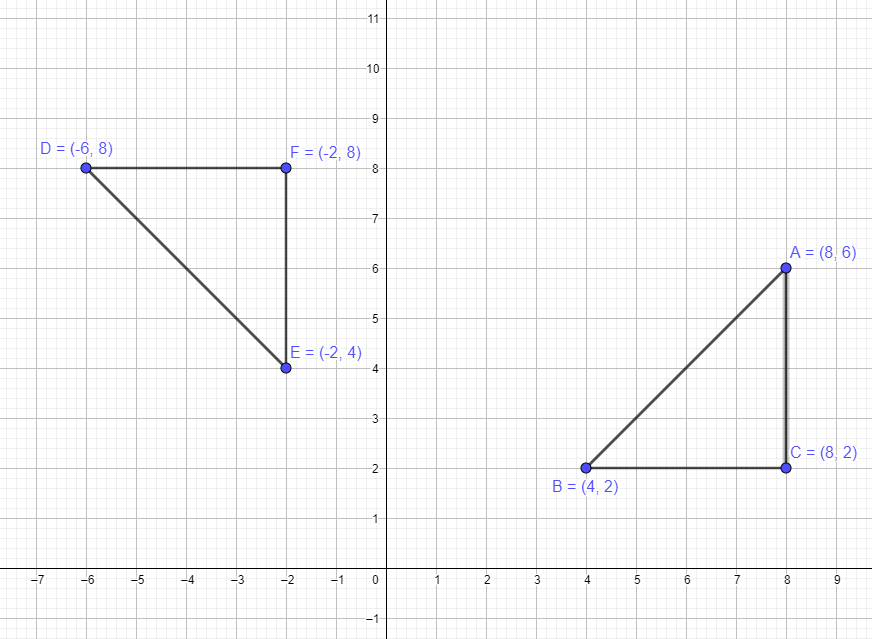
Similarly, if we move the polygon at 180 degree rotation, then the new points will be A $= (-8,-6)$, B $= (-4,-2)$ and C $= (-8,-2)$ and finally if we rotate it at 270 degree at clock-wise direction then the points will be A $= (6,-8)$ B $= (2,-4)$ and C $= (2,-8)$.
Now that you have an understanding of how rotation works, you will find it a lot easier to understand the concept of $-90^{o}$ rotation.
Practice Questions:
1. Rotate the following points by $-90^{o}$. a) $(6,1)$ b) $(-7,-6)$ c $(-2,3)$ d) $(3,-8 )$
2. You are given a Quadrilateral with vertices A $= (-1,9)$, B $= (-3,7)$ and C $= (-4,7)$ and D = $(-6,8)$. The quadrilateral is first rotated at 90^{o} clockwise, and then it is rotated at $90^{o}$ anti-clockwise. You are required to determine the value of coordinates after the final rotation.
Answer Keys:
1).
The new point after $-90^{o}$ rotation will be a) $(1,-6)$ b) $(-6, 7)$ c) $(3,2)$ d) $(-8,-3)$.
2).
The vertices of the quadrilateral are first rotated at 90 degrees clockwise and then they are rotated at 90 degrees anti-clockwise, so they will retain their original coordinates and the final form will same as given A= $(-1,9)$, B $= (-3,7)$ and C = $(-4,7)$ and D = $(-6,8)$.
