A rectangle is a flat (two dimensional) shape with four straight sides such that the length of the opposite sides are equal in measure and it possesses right angles for all of its interior angles. Therefore, both pairs of opposite sides are parallel and each side is perpendicular to all adjacent sides.
What Is a Rectangle?
A polygon having four sides or 4 corners are called a rectangle. If the edge-to-edge distance of all the sides of a polygon is equal in length, then the formed shape is known as a square. Whereas a rectangle has two pairs of equal-length sides, and the equal sides are opposite to each other, which differentiates it from a square.
Figure 1 – ABCD is the rectangle where AB is the length and AC is the width.
A rectangle is a two-dimensional shape, which means it can not be transformed into a 3D surface. In 3dimensional geometry, a rectangle is sometimes referred to as a cube. All the inner angles of a rectangle are equal in measure of 90$^{\circ}$. Since it is constructed in two dimensions, it is illustrated by two dimensions, length(L) and width(W).
Diagonals of a Rectangle
The line segment that begins from one vertex and ends at the opposite non-adjacent vertex is known as a diagonal. A rectangle has two diagonals that bisect each other at their point of intersection. Both diagonals are congruent and equal in length. They are not mutually perpendicular. A diagonal divides the rectangle into two right-angled triangles.
Figure 2 – Diagonals of a Rectangle
Finding the Length of a Diagonal
Consider the right angle triangle ABC, diagonal BC is the hypotenuse, AB (length) is the base, and AC (width) is the perpendicular of the triangle.
Let d represent the diagonal, l represents the length, and w represent the width. Then, by using Pythagoras’theorem, we have
Diagonal2 = length2 + width2
d2 = l2 + w2
d = $\sqrt{l^2 + w^2}$
Let’s take a look at how to find the length of diagonals of a rectangle having two sides of 10cm in length and the other two of 6cm in length. By using the formula,
d = $\sqrt{l^2 + w^2}$
= $\sqrt{10^2 + 6^2}$
= $\sqrt{100 + 36}$
= $\sqrt{136}$
d = 11.6 cm
Therefore, the length of both diagonals is 11.6cm.
Properties of Rectangle
Following are the properties of a rectangle
A rectangle is a quadrilateral.
It has 4 sides, 4 angles, and 4 vertices.
Opposite sides of a rectangle are equal.
Diagonals of a rectangle bisect each other.
The length of the diagonals is equal.
Each angle of the rectangle is 90 degrees.
If you sum up all the interior angles, the result would be 360 degrees.
The longer side of the rectangle is its length.
The shorter side of the rectangle is its width.
3D Rectangle
A 3-dimensional rectangle is called a rectangular prism and cuboid. It has 6 faces, 12 edges, and 8 vertices.
Area of Rectangle
The area of the rectangle is the entire region surrounded by the rectangle’sboundaries in a 2-dimensional plane. It is the product of length and width. The area occupied by rectangular-shaped objects such as a television, blackboard, door, refrigerator, etc., can easily be calculated by utilizing the formula for the area of a rectangle:
Area of rectangle = length * width
Consider an example of a television whose length is 42 inches and width is 20 inches. To figure out the exact area of a rectangle, we use the following formula,
Area = length * width
= 42 * 20
= 840 inch2
The Perimeter of a Rectangle
The perimeter of a rectangle is the path or distance covered by the boundary of the rectangle in a 2-dimensional plane. If two adjacent sides of a rectangle are summed up, we get the perimeter of a rectangle, which can be found using the mathematical formula given below,
Consider an example of a gardener who wants to find out how much wire would be required to put a fence around his garden. The length of the garden is 15 feet, and its width is 6 feet.
The answer to this problem can be found by calculating the perimeter of the garden as follows:
Length = 15 feet
Width = 6 feet
Perimeter = 2(length + width)
= 2(15 + 6)
= 2(21)
= 42 feet
Hence, 42 feet of wire would be required to put a fence around the garden.
Quadrilateral
A quadrilateral is a four-sided plane closed figure. It has four angles and four vertices. It is a (four-sided) polygon also known as a tetragon. The total measurement of all the interior angles comes out to be 360 degrees.
A quadrilateral is a combination of two Latin words, where Quadri stands for four, and lateral is described as sides. Hence, the name itself gives the description of this plane figure.
A rectangle is a type of quadrilateral. Some other types of quadrilaterals are square, parallelogram, rhombus, trapezium, and kite.
Square
A Square is a quadrilateral, but it differs from a rectangle as all of its sides are equal in length. Like a rectangle, a square has four equal angles of 90 degrees each. Diagonals of a square cross each other at a common point that has a 90-degree angle, thus bisecting each other perpendicularly.
Parallelogram
A parallelogram is a quadrilateral. It is like a rectangle, but its diagonals are unequal. Its opposite sides are parallel and equal. Diagonals bisect each other at the midpoint and shape two congruent triangles. A parallelogram has opposite equal angles.
We can say that a rectangle possesses all the mathematical properties of a parallelogram, but a parallelogram does not have all the properties of a rectangle. So a rectangle is a parallelogram, but a parallelogram may not be a rectangle.
Rhombus
A rhombus is a quadrilateral having all four sides equal, opposite sides parallel, and opposite angles equal. Diagonals of a rhombus cross each other at a common point that has a 90-degree angle, thus bisecting each other perpendicularly. All squares are rhombus, but the converse may not be true.
Trapezium
A trapezium is a combination of parallel and non-parallel sides. A quadrilateral having only one pair of non-adjacentparallel sides and having the other two as non-parallel sides is a trapezium. The sides that are parallel to each other are known as bases, whereas the other two non-parallel sides are known as legs. A parallelogram is a trapezium but a trapezium is not a parallelogram.
Kite
A kite is a four-sided figure, just like a tilted parallelogram but with two pairs of sides having equal lengths. If we draw the diagonals of a kite, they will behave just like a normal rectangular diagonal by intersecting each other at right angles.
The interior opposite angles of a kite are obtuse and equal in measure.
Solved Examples Involving Rectangular Shapes
Example 1
Find the length of a rectangle whose area is 400 feet2 and whose width is 16 feet.
Solution
Given:
Area = 400 feet2
Width = 16 feet
Length = ?
As we know that:
area = length * width
Putting the values of area and length in the above formula, we get:
400 = length * 16
400/16 = length
25 feet = length
Length = 25 feet
Therefore, the rectangle has an area of 400 feet and a width of 16 feet, has a length of 25 feet.
Example 2
A rectangular prism has a length of 20 inches and a width of 15 inches. Find the area and perimeter of the prism.
Figure 3 – Example of a Rectangular Prism
Solution
Given:
Length = 20 inches
Width = 15 inches.
Area =? ; Perimeter =?
For area, we have the formula:
Area = Length * Width
= 20 * 15
= 300 inches2
Now for perimeter, the formula is:
Perimeter = 2(length + width)
= 2(20 + 15)
= 2(35)
= 70 inches
Therefore, the rectangular prism has an area of 300 inches2 and a perimeter of 70 inches.
The rectangle, as a geometric shape, is a fundamental and widely recognized figure that plays a significant role in mathematics, architecture, design, and everyday life. With its straight sides, right angles, and symmetrical structure, the rectangle stands as a versatile shape with a myriad of applications and intriguing properties. Defined by its four sides of equal length, characterized by opposite sides that are parallel and all interior angles measuring 90 degrees, the rectangle embodies balance, stability, and geometric elegance.
We shall explore the fascinating world of rectangles in this post, exploring their geometry, properties, formulas, and practical applications. By unraveling the secrets of this geometric marvel, we aim to give them a clearer awareness of its importance. And inspire appreciation for the timeless beauty and utility that rectangles offer in various domains ofhuman endeavor.
Definition
A rectangle is a geometric shape that is characterized by its specific attributes. It has four right angles and is a quadrilateral, meaning each angle measures exactly 90 degrees. The term “rectangle” is derived from the Latin word “rectangulum,” which translates to “right angle.” In a rectangle, opposite sides are parallel and equal in length, and each pair of adjacent sides is perpendicular to one another.
The defining features of a rectangle make it a versatile and widely recognized shape. Its symmetrical nature and right angles contribute to its practical applications in various fields, including architecture, engineering, design, and mathematics. Below we present a generic diagram for a rectangle.
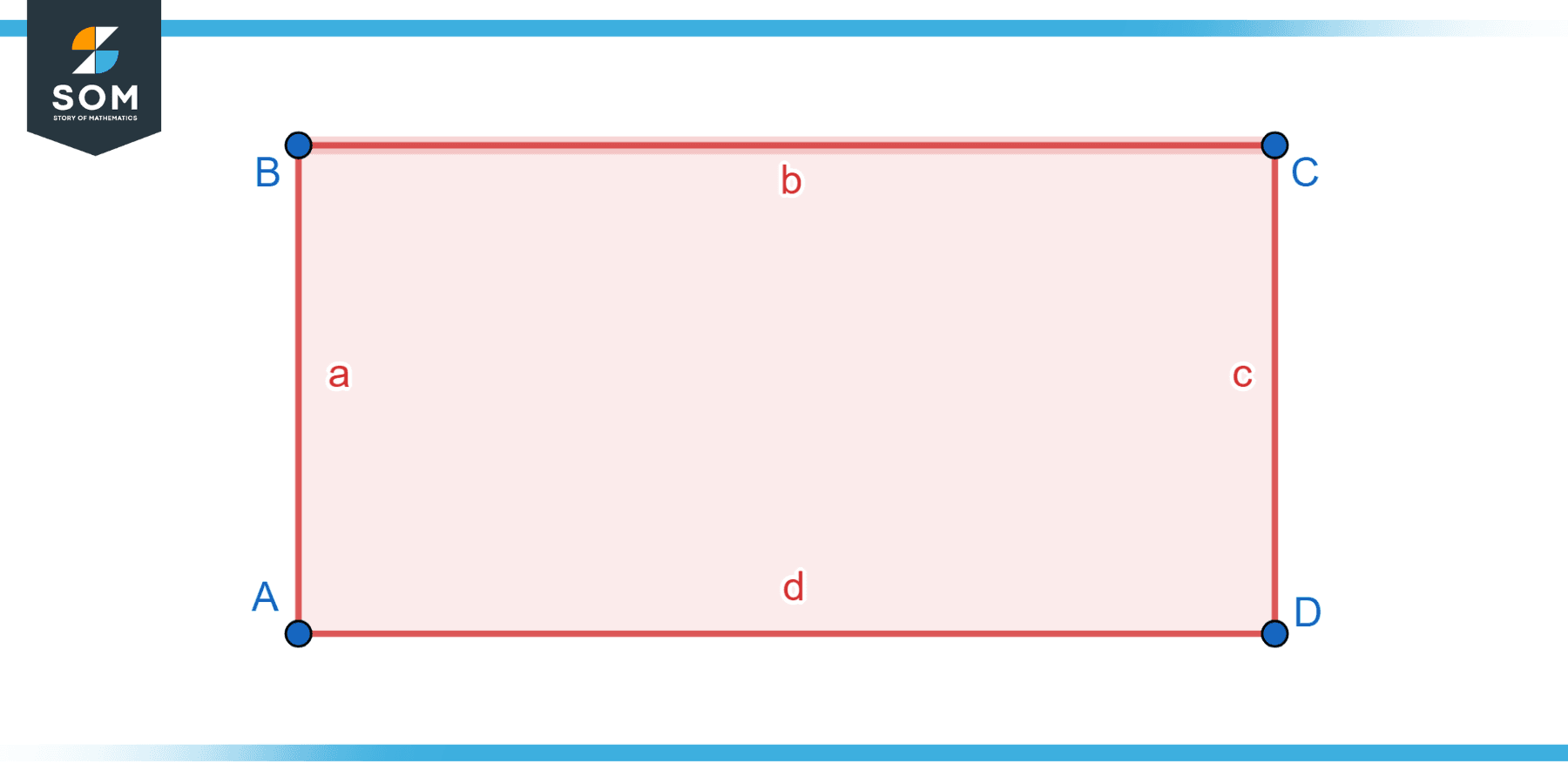
Figure-1: Generic rectangle.
Historical Significance
The historical background of the rectangle, a geometric shape, spans several centuries and is deeply intertwined with the development of mathematics and human civilization. The concept of the rectangle can be traced back to ancient civilizations, where early mathematicians and architects recognized its symmetry and practicality.
Ancient Mesopotamia
Ancient Mesopotamia is known to have utilized rectangular shapes in their architectural designs. Clay tablets dating back to around 2000 BCE reveal that ancient Mesopotamians were already familiar with rectangular structures and used them as the basis for constructing buildings, walls, and city plans. The regularity and stability of the rectangle made it a preferred shape for urban design.
Ancient Egypt
In Ancient Egypt, the use of rectangles can be seen in the construction of pyramids and other monumental structures. The Egyptians were skilled in the art of measurement and geometry, and rectangles played a crucial role in their architectural endeavors. The precision and right angles of rectangles contributed to the stability and grandeur of their architectural achievements.
Ancient Greece
The study of geometry flourished in Ancient Greece, where prominent mathematicians like Euclid made significant contributions to our understanding of rectangles. Euclid’s work in his influential mathematical treatise, “Elements,” provided a systematic framework for studying rectangles and their properties. He established the foundational principles of geometry, including theorems and proofs related to rectangles, which laid the groundwork for future mathematical advancements.
Renaissance Period
During the Renaissance period, advancements in mathematics and the revival of classical knowledge further expanded our understanding of rectangles. Renowned mathematicians like Leonardo da Vinci and Albrecht Dürer incorporated geometric principles into their artistic works, emphasizing the significance of rectangles in achieving balance and perspective in art and architecture.
18th-Century Mathematicis
The study of rectangles continued to evolve throughout history, with 18th-century mathematicians developing formulas and theorems related to the measurement of rectangles, their areas, perimeters, and diagonal lengths. These advancements paved the way for practical applications of rectangles in fields such as engineering, construction, and design.
In the modern era, rectangles remain a fundamental shape in mathematics and continue to find widespread use in various disciplines. They are extensively employed in architecture, urban planning, computer graphics, manufacturing, and even everyday objects such as books, windows, and electronic screens. The rectangular shape’s stability, symmetry, and versatility make it a cornerstone of both practical and aesthetic design.
Properties
Here are the properties of a rectangle, a geometric shape, explained in detail.
Equal Opposite Sides
A rectangle has opposite sides that are parallel and equal in length. As a result, the length of one set of diagonals is equal to the length of the other set of diagonals.
Right Angles
All four angles in a rectangle are right angles. A right angle measures exactly 90 degrees. The presence of right angles gives the rectangle its characteristic shape and symmetry.
Parallel and Congruent Diagonals
The diagonals of a rectangle are congruent (i.e., they have the same length) and bisect each other. Furthermore, the diagonals are parallel to the opposite sides of the rectangle.
Equal Opposite Angles
The opposite angles in a rectangle are congruent, meaning they have the same measure. Each pair of opposite angles in a rectangle measures 90 degrees.
Perpendicular Bisectors
The diagonals of a rectangle serve as perpendicular bisectors of each other. This means that the diagonals divide each other into two equal parts and intersect at a right angle.
Symmetry
A rectangle exhibits line symmetry or mirror symmetry. It can be folded along its center line so that both halves coincide perfectly, creating two congruent mirror images.
Area and Perimeter
The area of a rectangle can be calculated using the formula: Area = length × width. The perimeter of a rectangle can be calculated using the formula: Perimeter = 2 × (length + width).
Duality with Parallelograms
A rectangle is a special type of parallelogram, which means it shares some properties with parallelograms. However, unlike a general parallelogram, a rectangle has additional properties, such as all angles being right angles.
Understanding these properties of a rectangle allows for a comprehensive exploration of its geometry, relationships between sides and angles, and practical applications. These properties provide a foundation for various mathematical calculations and enable the utilization of rectangles in diverse fields, including architecture, engineering, construction, and design.
Related Formulas
Certainly! Here are the related formulas of a rectangle, along with a detailed explanation of each:
Area (A)
The area of a rectangle is the measure of the region enclosed by its sides. It can be calculated using the formula: A = length × width. The area is given in square units, such as square centimeters, square meters, or square inches.
Perimeter (P)
The perimeter of a rectangle is the total length of its sides. It can be calculated using the formula: P = 2 × (length + width). The perimeter is given in linear units, such as centimeters, meters, or inches.
Diagonal length (d)
The diagonal of a rectangle is that line segment that connects two non-contiguous vertices.The diagonal’s length can be calculated using the Pythagorean theorem. In a rectangle, the diagonal, length, and width form a right triangle. The formula to calculate the diagonal length is d = √(length² + width²). Below we present a generic representation of the diagonals of a rectangle.
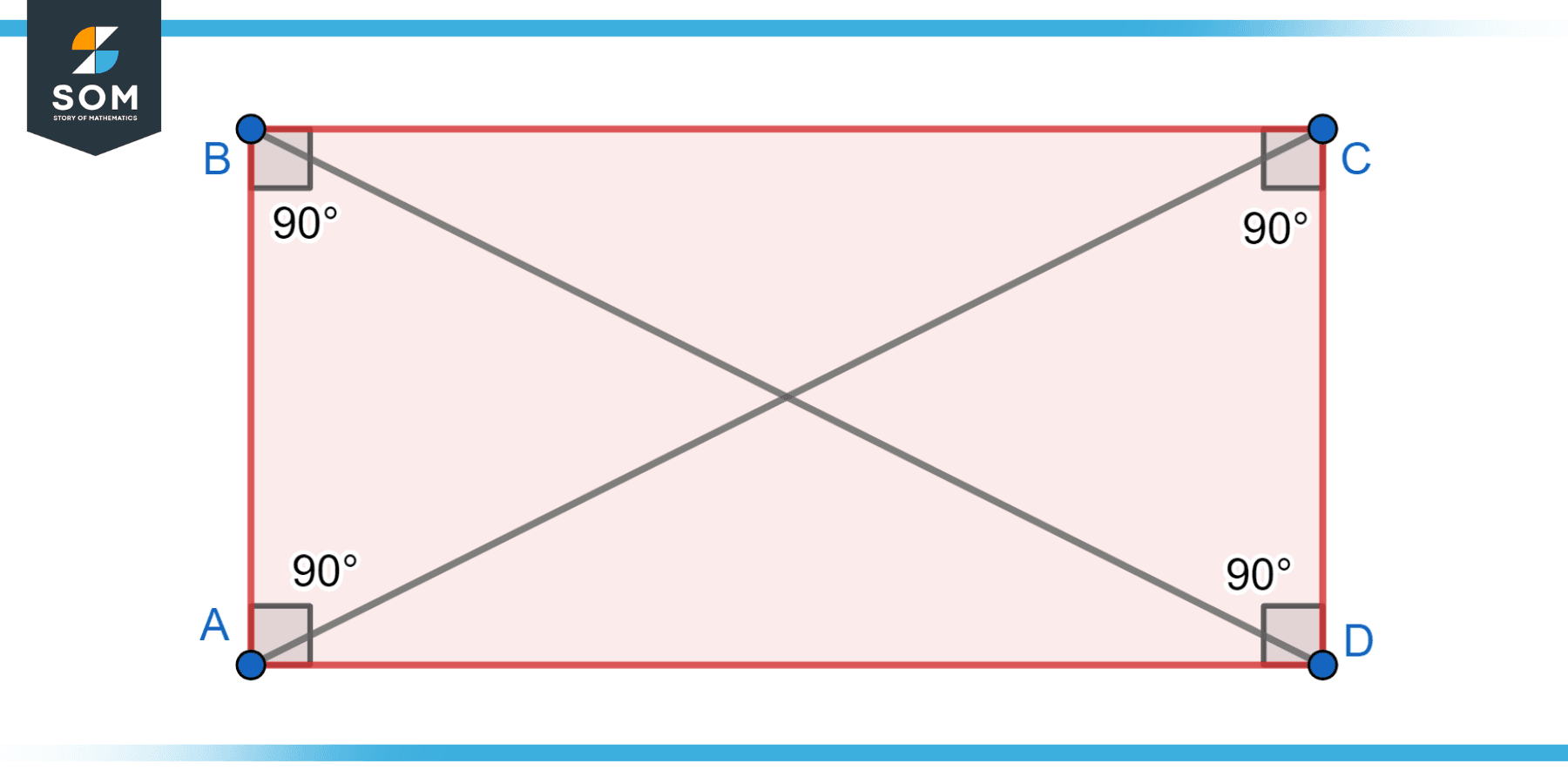
Figure-2: Generic representation of the diagonals of a rectangle.
Relationship Between Area and Diagonal Length
There is a relationship between the area of a rectangle and the length of its diagonal. The formula to calculate the diagonal length based on the area is d = √(4 × A) / √(π). This formula applies when the area is known and can be useful in certain contexts.
Relationship Between Perimeter and Length/Width
The perimeter of a rectangle is directly related to its length and width. If the length and width are known, the following formula can be used to get the perimeter: P = 2 × (length + width). Conversely, if the perimeter and one of the side lengths are known, the other side length can be found using the formula: length/width = (P – 2 × known side length) / 2.
Relationship Between Area and Perimeter
There is an inverse relationship between the area and perimeter of a rectangle. Given a fixed perimeter, the rectangle with the maximum area is a square, where all sides are equal. Similarly, given a fixed area, the rectangle with the minimum perimeter is also a square.
Golden Ratio
The golden ratio is a special ratio that occurs in rectangles, particularly in the golden rectangle. In a golden rectangle, the ratio of the longer side to the shorter side is about equal to the the Golden Ratio, denoted by the Greek letter phi (φ), which is approximately 1.61803398875.
Length or Width Calculation
If the area and one side length (either length or width) of a rectangle are known, you can solve for the missing side using the formula A = length × width. Rearranging the formula, you can calculate the missing side length by dividing the area by the known side length. For example, if the area (A) and length (L) are given, the formula to find the width (W) is W = A / L.
Types
There are several types of rectangles that can be distinguished based on different properties and characteristics. Here are some key types of rectangles.
Square
A square is a special type of rectangle where all four sides are equal in length. In other words, it is a rectangle with all right angles and all sides of equal length. The properties of squares make them highly symmetric and suitable for applications where equal dimensions are desired. Below we present a square rectangle.
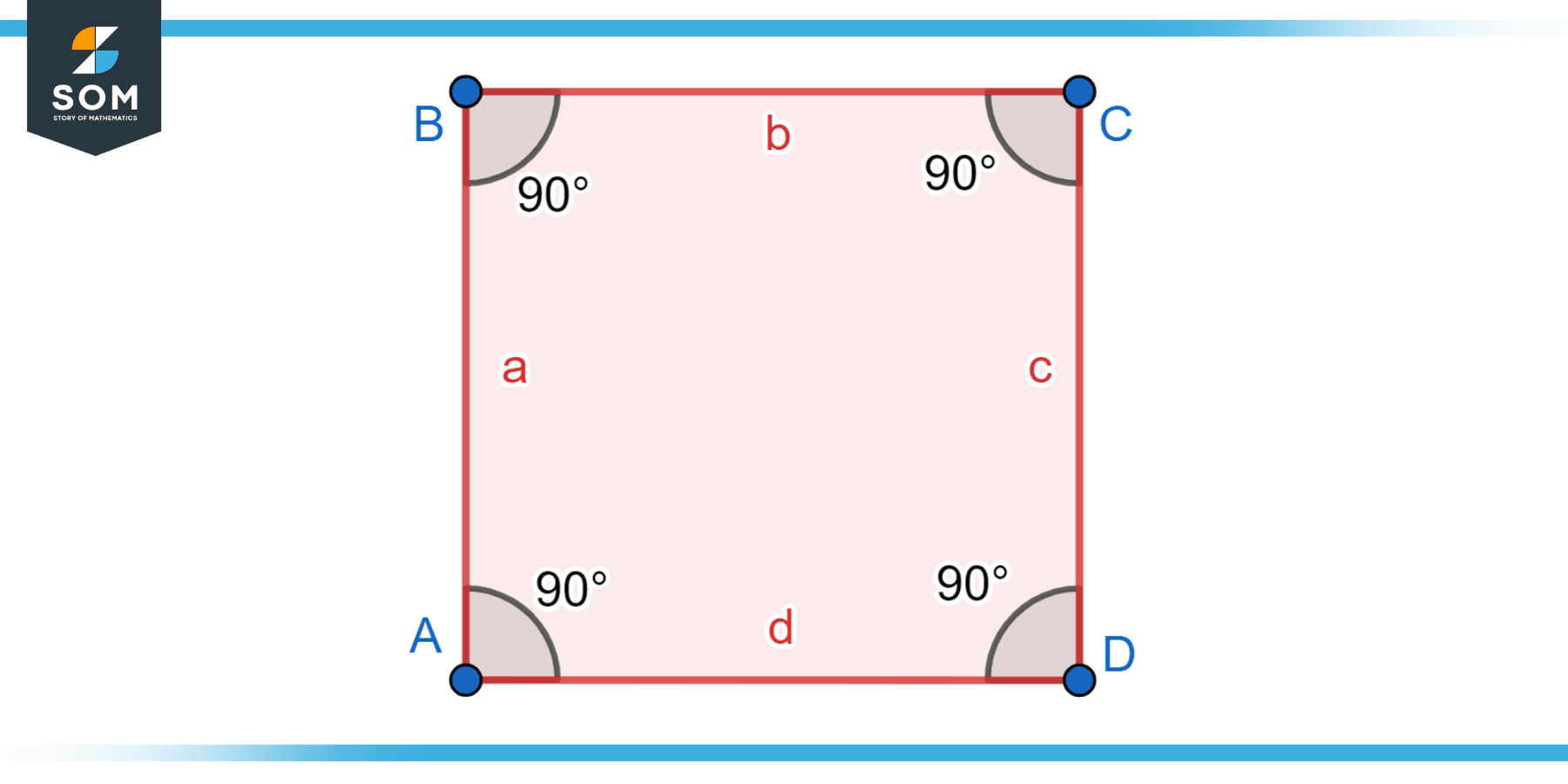
Figure-3: Square rectangle.
Oblique Rectangle
An oblique rectangle, also known as an oblong, is a rectangle with unequal adjacent sides. While all four angles are still right angles, the lengths of the adjacent sides differ. Unlike a square, the sides are not equal in length. Below we present an oblique rectangle.
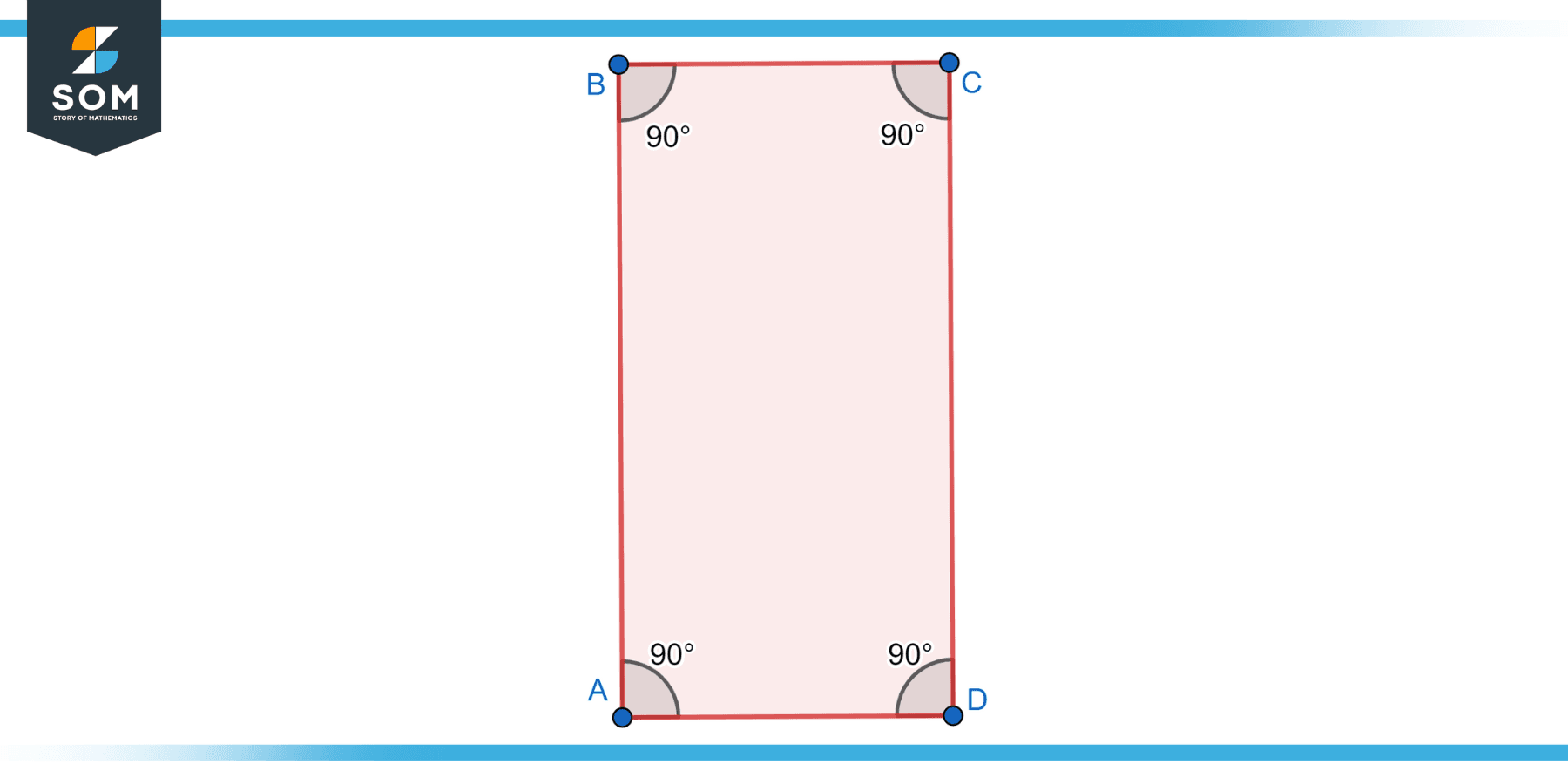
Figure-4: Oblique rectangle.
Golden Rectangle
A golden rectangle is a rectangle with the special property that the ratio of its longer side (length) to its shorter side (width) is equal to the golden ratio, approximately 1.618. This ratio is believed to possess aesthetic and harmonious qualities and has been employed in art, architecture, and design throughout history. Below we present a golden rectangle.
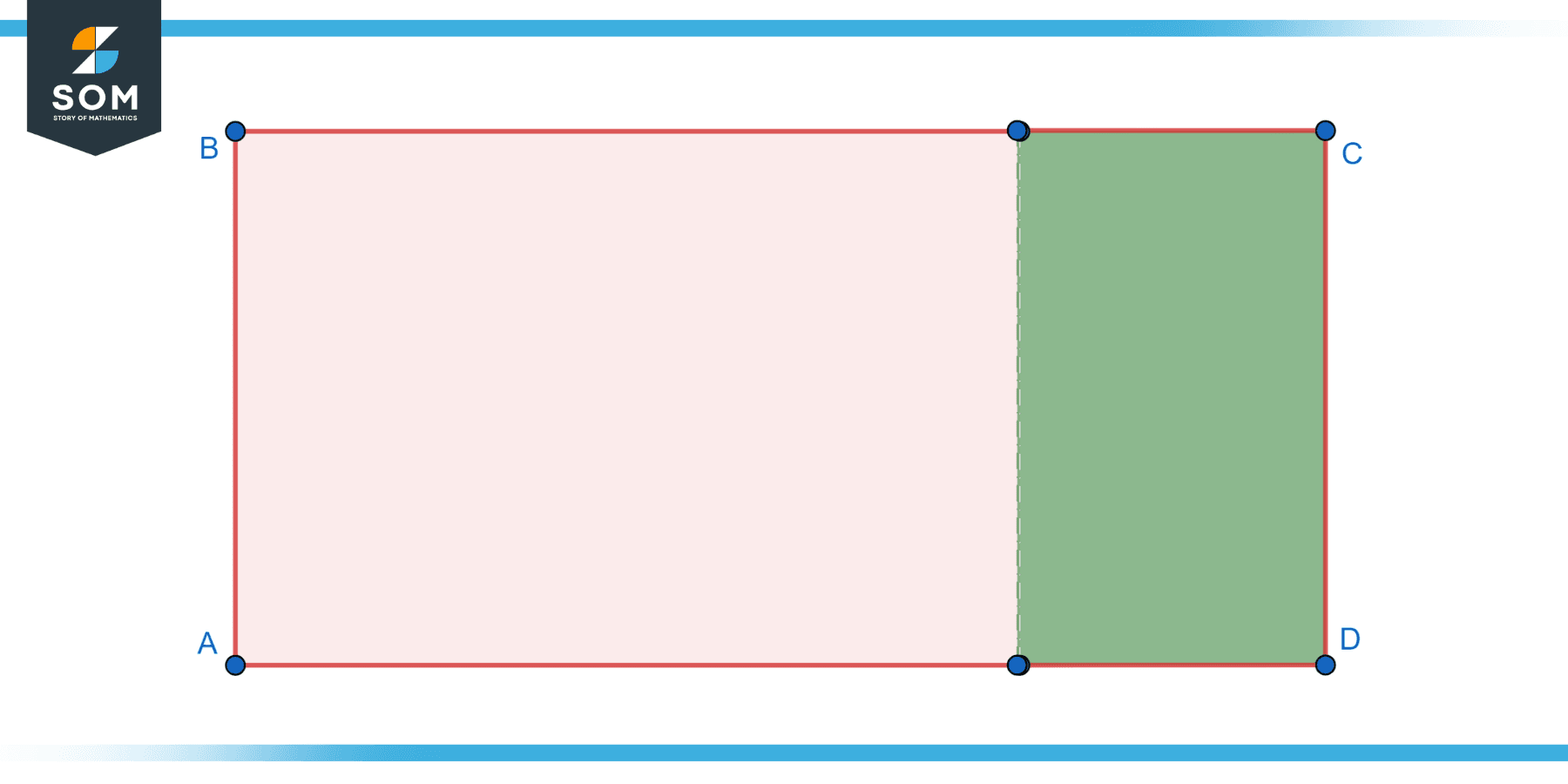
Figure-5: Golden rectangle.
Proportional Rectangle
A proportional rectangle is a rectangle in which the ratio of the length to the width is a specific value. Proportional rectangles can be designed to fit specific dimensional requirements or adhere to certain geometric constraints. Below we present a proportional rectangle.
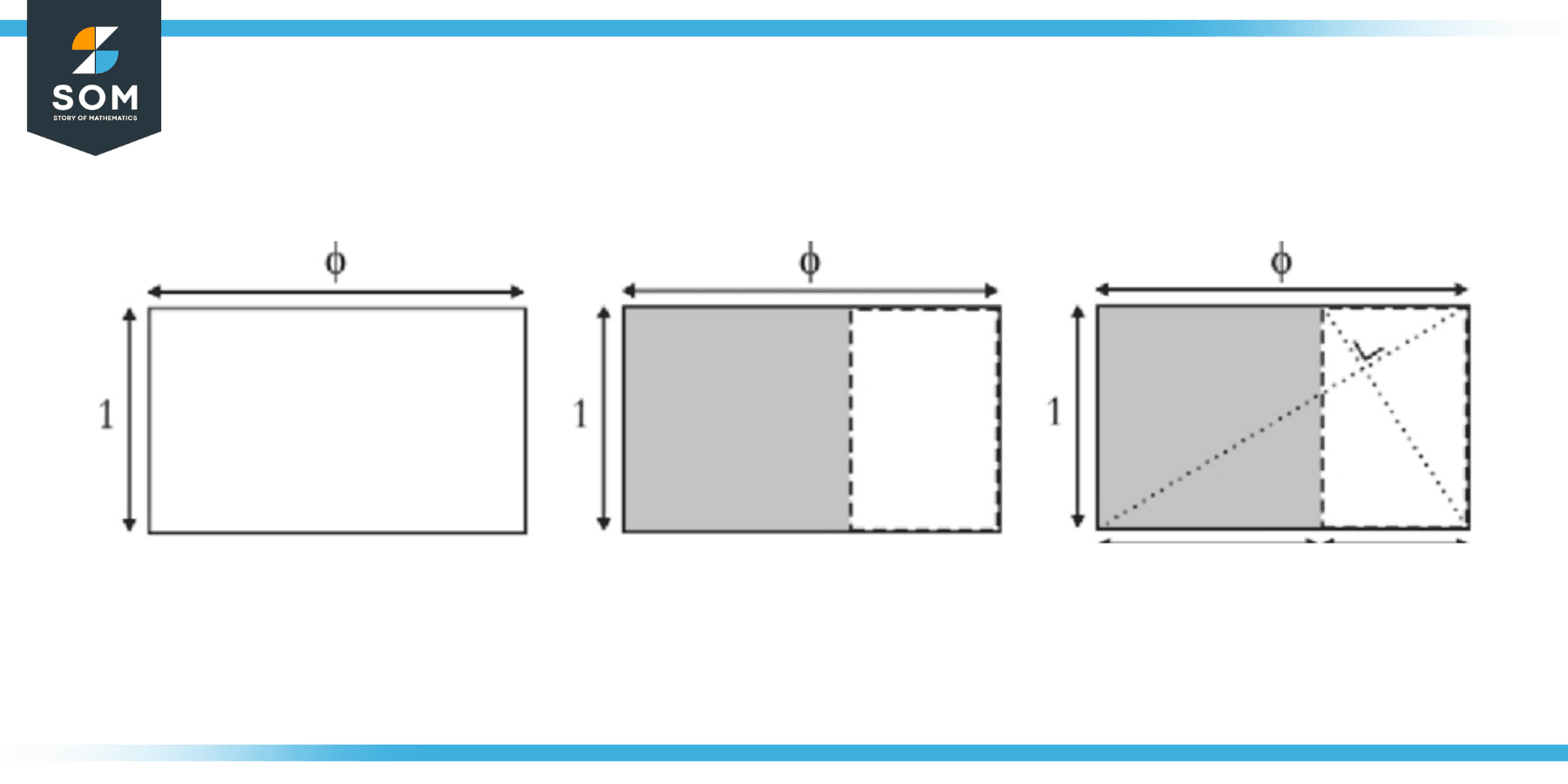
Figure-6: Proportional rectangle.
Each type of rectangle has its own unique characteristics and may have different applications or significance in various fields.
Applications
The rectangle, as a geometric shape, finds extensive applications in various fields due to its specific properties and characteristics. Here are some notable applications of the rectangle in different domains.
Architecture and Construction
Rectangles play a fundamental role in architecture and construction. They are commonly used as the basis for designing floor plans, building foundations, and structural elements. The regularity and symmetry of rectangles make them suitable for creating balanced and aesthetically pleasing structures.
Engineering and Design
In engineering and design disciplines, rectangles are widely employed in the design of machinery, mechanical components, electrical circuit boards, and architectural elements. The shape of rectangles allows for efficient utilization of space and facilitates standardized manufacturing processes.
Graphic Design and Art
Rectangles serve as a foundational element in graphic design and art. They are used for creating layouts, frames, borders, and compositions. The regularity and simplicity of rectangles provide a structured framework for organizing and presenting information or visual elements.
Mathematics and Geometry
Rectangles are extensively studied in mathematics and geometry. They serve as a fundamental shape for understanding concepts such as area, perimeter, volume, and surface area. Rectangles also form the basis for advanced geometric shapes and concepts, including squares, oblongs, and parallelograms.
Computer Graphics and User Interfaces
Rectangles are widely used in computer graphics and user interfaces. Display screens, windows, buttons, and frames often take the form of rectangles. The rectangular shape provides a familiar and intuitive interface for users to interact with digital systems.
Photography and Film
In photography and film, the concept of the “rule of thirds” involves dividing the frame into a grid of rectangles. This composition technique helps create visually balanced and aesthetically pleasing images by placing important elements along the lines or intersections of the grid.
Furniture and Product Design
Rectangular shapes are commonly found in furniture and product design. Tables, desks, cabinets, and many other items are often designed with rectangular surfaces and structures. The practicality and versatility of rectangles make them suitable for creating functional and ergonomic designs.
Education and Teaching
Rectangles are frequently used in educational materials and teaching aids to introduce concepts of geometry, measurements, and spatial relationships. They provide a visual representation that aids in understanding mathematical principles and properties.
The applications of rectangles span various fields, highlighting their versatility, practicality, and widespread use. Their regularity, symmetry, and well-defined properties make them a fundamental shape with a broad relevance in many disciplines.
Exercise
Example 1
Find the area of a rectangle with a length of 6 units and a width of 4 units.
Solution
Given: Length = 6 units Width = 4 units
To find the area (A) of a rectangle, we can use the formula:
A = length × width
A = 6 units × 4 units
A = 24 square units
Therefore, the area of the rectangle is 24 square units.
Example 2
Determine the perimeter of a rectangle with a length of 12 meters and a width of 8 meters.
Solution
Given: Length = 12 meters Width = 8 meters
To find the perimeter (P) of a rectangle, we can use the formula:
P = 2 × (length + width)
P = 2 × (12 meters + 8 meters)
P = 2 × 20 meters P = 40 meters
Therefore, the perimeter of the rectangle is 40 meters.
Example 3
Calculate the length of a diagonal in a rectangle with sides measuring 5 centimeters and 12 centimeters.
Solution
Given: Side lengths: 5 centimeters and 12 centimeters
To find the length of the diagonal, we can use the Pythagorean theorem. In a rectangle, the diagonal, side lengths, and right angles form a right triangle.
Using the formula:
diagonal² = length² + width²
diagonal² = 5² + 12²
diagonal² = 25 + 144
diagonal² = 169
Taking the square root of both sides, we find diagonal = √169 diagonal = 13 centimeters.
Therefore, the length of the diagonal in the rectangle is 13 centimeters.
Example 4
Given the diagonal length of a rectangle as 10 units and one side length as 6 units, as shown in Figure-7. Find the length of the other side.
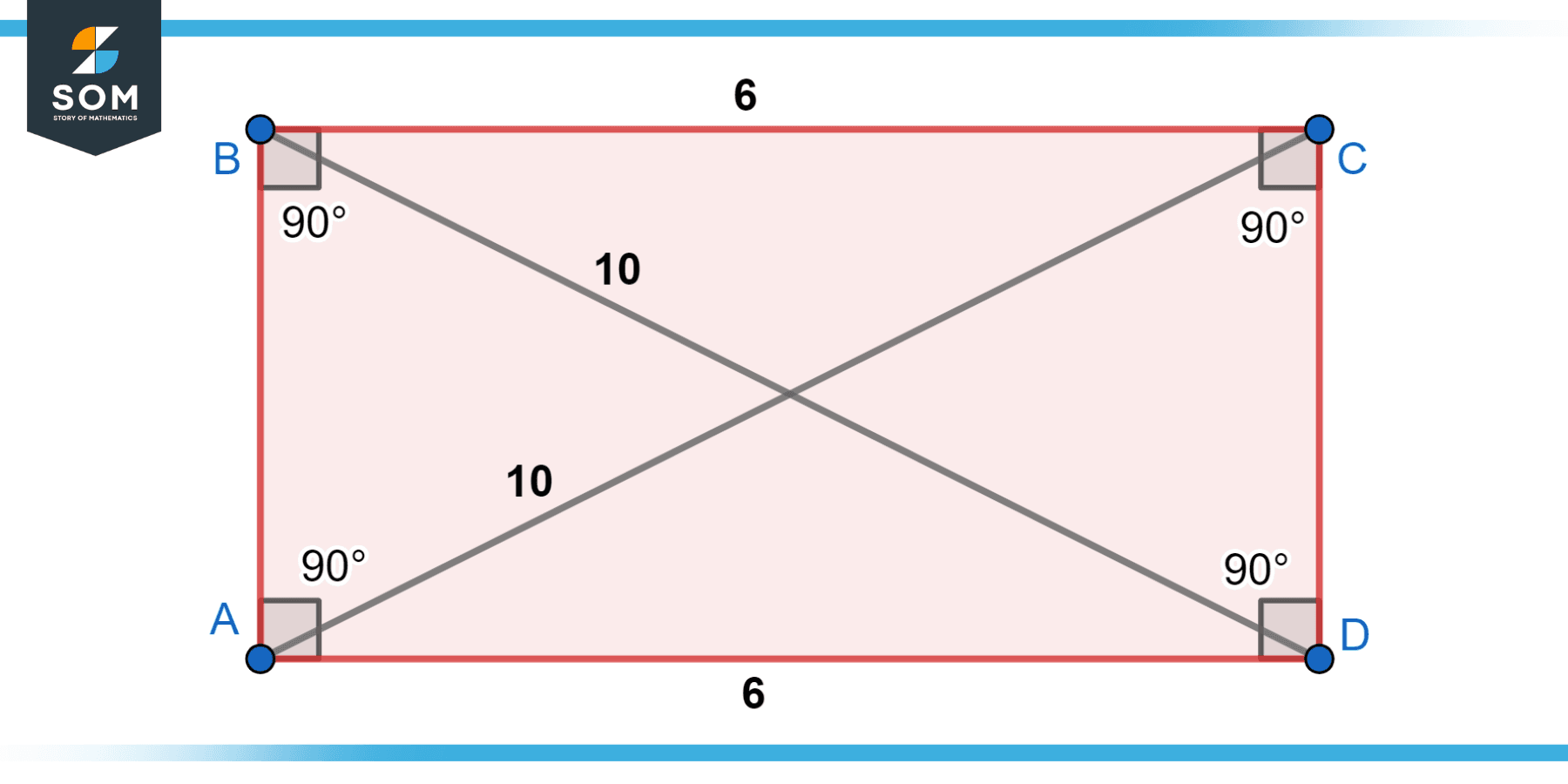
Figure-7.
Solution
Given: Diagonal length = 10 units and One side length = 6 units
To find the length of the other side, we can use the Pythagorean theorem.
Let the length of the other side be x. Using the formula:
diagonal² = length² + width²
10² = 6² + x²
100 = 36 + x²
x² = 100 – 36
x² = 64
x = √64
x = 8 units
Therefore, the length of the other side of the rectangle is 8 units.
Example 5
Find the length of a rectangle whose area is 72 square centimeters and width is 6 centimeters.
Solution
Given: Area = 72 square centimeters Width = 6 centimeters
To find the length (L) of the rectangle, we can rearrange the formula for the area of a rectangle:
A = length × width.
Substituting the given values: 7
2 = L × 6 L
72 / 6 L = 12 centimeters
Therefore, the length of the rectangle is 12 centimeters.
Example 6
Determine the width of a rectangle whose area is 48 square meters and length is 12 meters.
Solution
Given: Area = 48 square meters Length = 12 meters
To find the width (W) of the rectangle, we can rearrange the formula for the area of a rectangle:
A = length × width.
Substituting the given values:
48 = 12 × W
W = 48 / 12
W = 4 meters
Therefore, the width of the rectangle is 4 meters.
Example 7
Calculate the perimeter of a rectangle with an area of 35 square units and a length of 7 units.
Solution
Given: Area = 35 square units Length = 7 units
To find the width (W) of the rectangle, we can rearrange the formula for the area of a rectangle:
A = length × width.
Substituting the given values:
35 = 7 × W
W = 35 / 7
W = 5 units
To find the perimeter (P) of the rectangle, we can use the formula:
P = 2 × (length + width)
P = 2 × (7 + 5)
P = 2 × 12
P = 24 units
Therefore, the perimeter of the rectangle is 24 units.
Example 8
Given the perimeter of a rectangle as 30 meters and one side length as 8 meters, find the length of the other side.
Solution
Given: Perimeter = 30 meters One side length = 8 meters
To find the length of the other side, we can use the formula for the perimeter of a rectangle:
P = 2 × (length + width).
Substituting the given values:
30 = 2 × (8 + W)
15 = 8 + W
W = 15 – 8
W = 7 meters
Therefore, the length of the other side of the rectangle is 7 meters.
