
The trapezoid midsegment is a line segment connecting the midpoints of a trapezoid’s non-parallel sides. Exploring trapezoids’ fascinating properties and geometric characteristics can lead us to uncover hidden gems within their structures.
The trapezoid midsegment holds a special place in the realm of geometry, as it not only reveals intriguing relationships within the trapezoid itself but also serves as a gateway to understanding broader concepts in mathematics.
In this article, we will delve into the properties and applications of the trapezoid midsegment, unlocking its secrets and shedding light on its significance in various geometric contexts.
Definition of Trapezoid Midsegment
The trapezoid midsegment is a line segment connecting the midpoints of a trapezoid’s non-parallel sides. In other words, it is a segment that joins the midpoint of one of the non-parallel sides with the midpoint of the other non-parallel side.
The trapezoid midsegment is always parallel to the trapezoid’s bases and is halfway between them. It divides the trapezoid into two equal-area and congruent triangles. The length of the trapezoid midsegment is equal to the average of the lengths of the trapezoid’s bases.
Below we present a generic representation of the trapezoid and its midsegment line in figure-1.
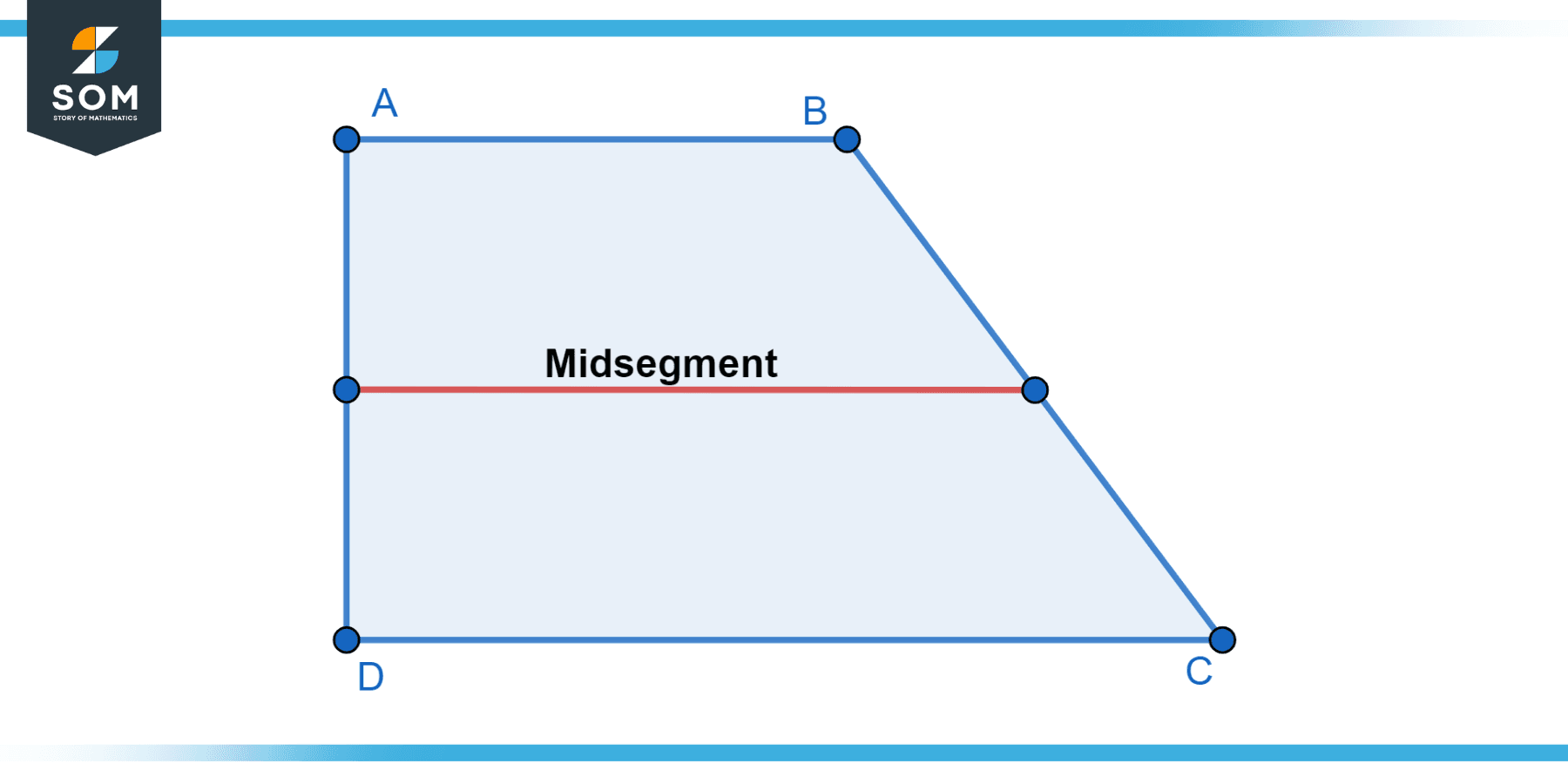
Figure-1.
Properties
Here are the properties of the trapezoid midsegment explained in detail:
Parallelism
The trapezoid midsegment is always parallel to the trapezoid’s bases. This means the midsegment and the bases never intersect and share the same slope.
Length
The length of the trapezoid midsegment is equal to the average of the lengths of the trapezoid’s bases. Let’s denote the lengths of the two bases as a and b. Then, the midsegment (m) length can be calculated as m = (a + b) / 2.
Midpoint
The trapezoid midsegment connects the midpoints of the non-parallel sides of the trapezoid. This implies that it divides the non-parallel sides into two equal segments. Additionally, the midsegment has a midpoint equidistant from both bases.
Congruence
The trapezoid midsegment divides the trapezoid into two equal-area and congruent triangles. These triangles are formed by the midsegment and each of the trapezoid’s bases.
Proportions
The lengths of the trapezoid’s bases are proportional to the lengths of the sides formed by the midsegment. Specifically, if the lengths of the bases are denoted as a and b, and the lengths of the sides formed by the midsegment are denoted as c and d, then a/c = b/d.
Triangle Area Relationship
The area of each triangle formed by the trapezoid midsegment and one of the bases is equal to half the product of the base length and the length of the midsegment. The area of each triangle can be calculated as (1/2) * base * midsegment.
Transversal Properties
If a line intersects the trapezoid and forms parallel segments with the bases, the segments formed on the bases are proportional to the lengths of the sides formed by the midsegment. Specifically, if the segments formed on the bases are denoted as x and y, and the lengths of the sides formed by the midsegment are denoted as c and d, then x/y = c/d.
These properties of the trapezoid midsegment provide valuable insights into the geometric relationships and characteristics of trapezoids, allowing for further exploration and analysis in various mathematical contexts.
Applications
While the trapezoid midsegment may not have direct applications in specific fields, its properties, and geometric relationships have broader implications in various areas of mathematics and beyond. Here are a few examples:
Geometry and Spatial Reasoning
Studying the trapezoid midsegment helps develop spatial reasoning skills and enhances geometric understanding. It allows for a deeper exploration of trapezoid properties and relationships, which can be applied in solving geometric problems and proofs.
Architecture and Engineering
Understanding the trapezoid midsegment can be useful in architectural and engineering applications. It provides insights into trapezoidal structures and their properties, which can influence the design, stability, and load distribution in architectural and engineering projects.
Computer Graphics and Modeling
Trapezoid midsegments and other geometric concepts are employed in computer graphics and modeling. Algorithms and techniques used in 3D modeling and rendering often rely on geometric properties and relationships, including those of trapezoids, to create realistic and accurate visual representations.
Mathematics Education
The mathematics curriculum often includes the study of trapezoid midsegments to promote geometric thinking, logical reasoning, and problem-solving skills. Exploring the properties of trapezoids and their midsegments can foster a deeper understanding of geometry concepts among students.
Applied Mathematics and Physics
The concepts and principles learned through studying trapezoid midsegments can be applied to various mathematical and physical phenomena. These principles can contribute to analyzing and modeling real-world situations, such as analyzing forces in trapezoidal structures or studying wave propagation in trapezoidal channels.
Pattern Recognition and Machine Learning
Geometric concepts, including those related to trapezoid midsegments, play a role in pattern recognition and machine learning algorithms. Understanding the geometric properties of shapes, such as trapezoids, can aid in feature extraction, shape recognition, and classification tasks.
While the direct applications of trapezoid midsegments may not be evident in specific fields, the underlying geometric principles and problem-solving skills developed through their study have broad applications across various disciplines. The ability to analyze and understand geometric structures and relationships contributes to critical thinking, problem-solving, and the development of mathematical intuition.
Exercise
Example 1
In trapezoid ABCD, AB || CD, and the length of AB is 10 units. The length of the midsegment EF is 8 units. Find the length of the CD.
Solution
EF is the midsegment and is parallel to AB and CD. Therefore, EF is also parallel to CD. We know that:
EF = (AB + CD) / 2
Substituting the given values, we have:
8 = (10 + CD) / 2
Solving for CD, we get CD = 6 units.
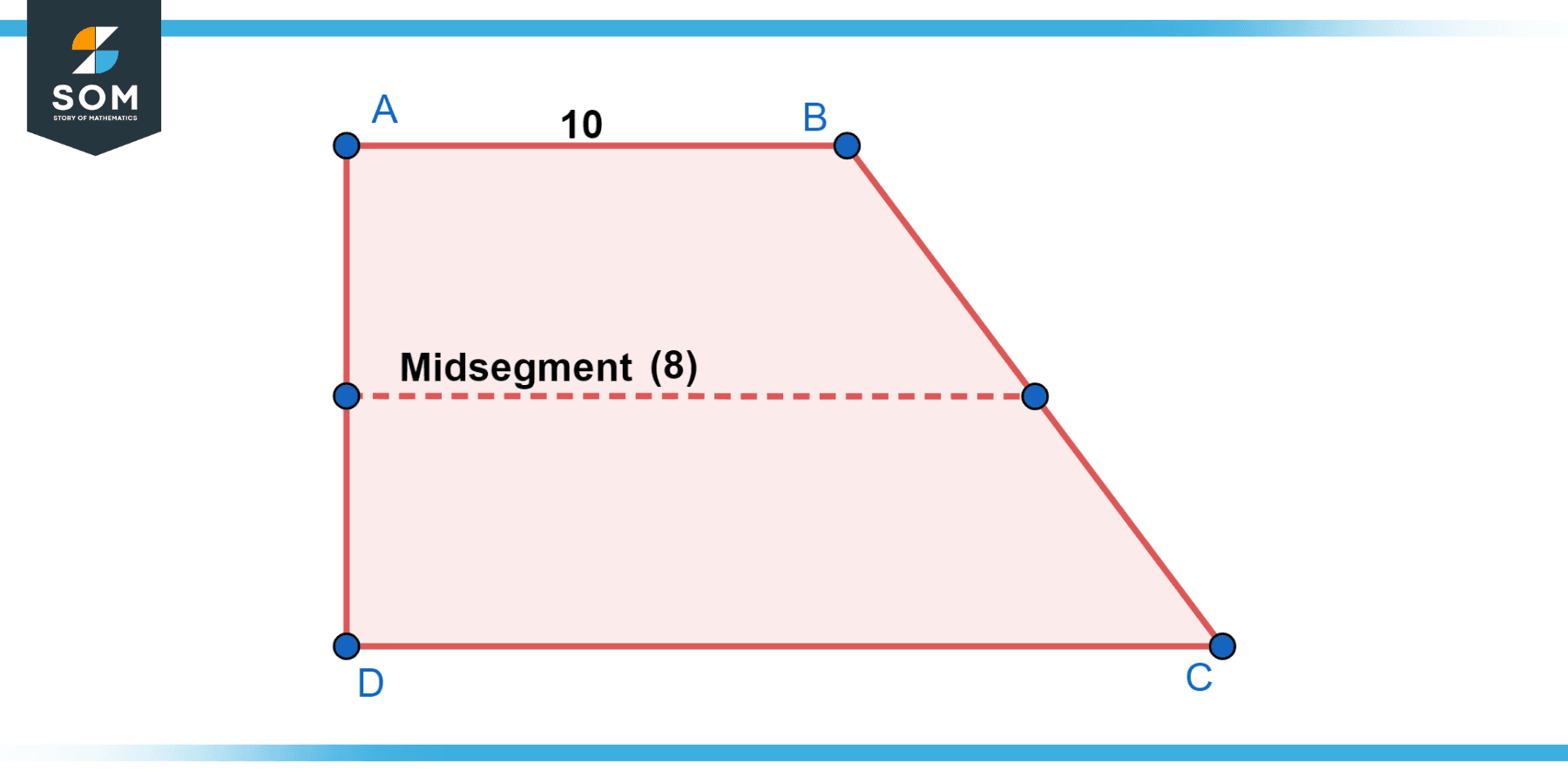
Figure-2.
Example 2
In trapezoid, PQRS, the length of QR is 12 units, and PS is 6 units. If the midsegment EF is parallel to QR and PS, and EF = 9 units, find the length of RS.
Solution
Since EF is the midsegment, it is parallel to QR and PS. Therefore, it is also parallel to RS. We know that:
EF = (QR + RS) / 2
Substituting the given values, we have:
9 = (12 + RS) / 2
Solving for RS, we get RS = 6 units.
Example 3
In trapezoid LMNO, the length of LM is 5 units, and the length of the midsegment PQ is 9 units. Find the length of NO, given that NO is parallel to LM.
Solution
Since PQ is the midsegment, it parallels LM and NO. Therefore, it is also parallel to NO. We know that:
PQ = (LM + NO) / 2
Substituting the given values, we have:
9 = (5 + NO) / 2
Solving for NO, we get NO = 13 units.
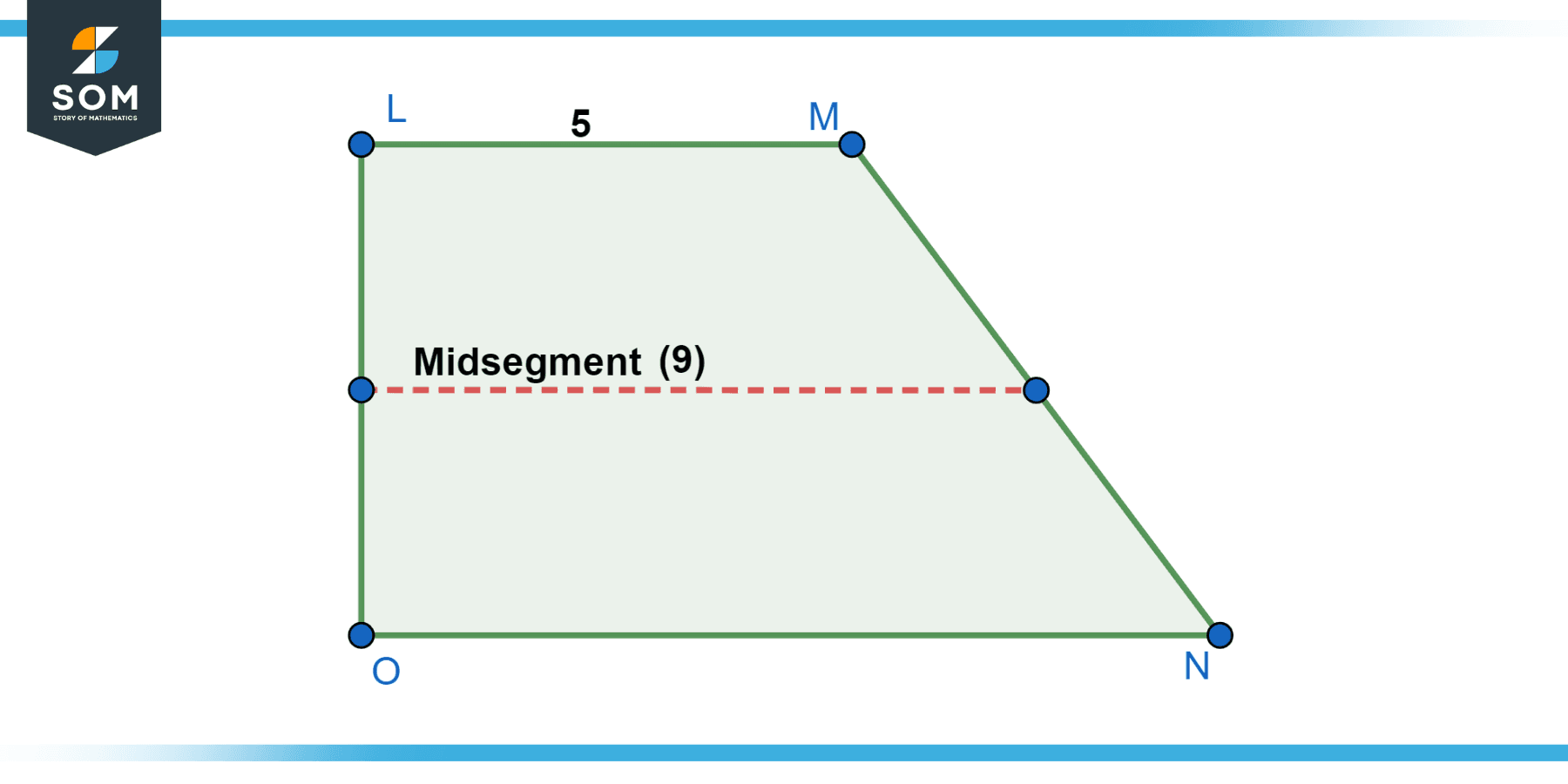
Figure-3.
Example 4
In trapezoid XYZW, the length of XY is 8 units, and the length of the midsegment UV is 6 units. Find the length of WZ, given that WZ is parallel to XY.
Solution
UV is the midsegment and is parallel to XY and WZ. Therefore, it is also parallel to WZ. We know that:
UV = (XY + WZ) / 2
Substituting the given values, we have:
6 = (8 + WZ) / 2
Solving for WZ, we get WZ = 4 units.
Example 5
In trapezoid ABCD, AB || CD, and the length of AB is 12 units. If the midsegment EF is parallel to AB and CD and EF = 7 units, find the length of CD.
Solution
EF is the midsegment and is parallel to AB and CD. Therefore, EF is also parallel to CD. We know that:
EF = (AB + CD) / 2
Substituting the given values, we have:
7 = (12 + CD) / 2
Solving for CD, we get CD = 2 units.
Example 6
In trapezoid, PQRS, the length of QR is 15 units, and PS is 9 units. If the midsegment EF is parallel to QR and PS and EF = 12 units, find the length of RS.
Solution
Since EF is the midsegment, it is parallel to QR and PS. Therefore, it is also parallel to RS. We know that:
EF = (QR + RS) / 2
Substituting the given values, we have:
12 = (15 + RS) / 2
Solving for RS, we get RS = 9 units.
Example 7
In trapezoid LMNO, the length of LM is 6 units, and the length of the midsegment PQ is 10 units. Find the length of NO, given that NO is parallel to LM.
Solution
Since PQ is the midsegment, it parallels LM and NO. Therefore, it is also parallel to NO. We know that:
PQ = (LM + NO) / 2
Substituting the given values, we have:
10 = (6 + NO) / 2
Solving for NO, we get NO = 14 units.
Example 8
In trapezoid XYZW, the length of XY is 10 units, and the length of the midsegment UV is 8 units. Find the length of WZ, given that WZ is parallel to XY.
Solution
UV is the midsegment and is parallel to XY and WZ. Therefore, it is also parallel to WZ. We know that:
UV = (XY + WZ) / 2
Substituting the given values, we have:
8 = (10 + WZ) / 2
Solving for WZ, we get WZ = 6 units.
All images were created with GeoGebra.
